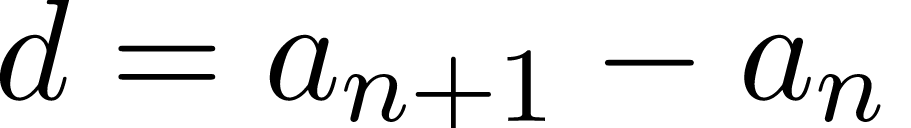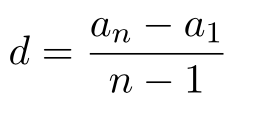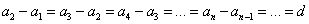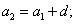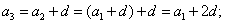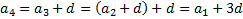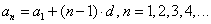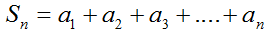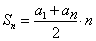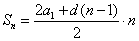Что такое гипотетическая прогрессия
ГИПОТЕТИЧЕСКИЙ
Смотреть что такое «ГИПОТЕТИЧЕСКИЙ» в других словарях:
ГИПОТЕТИЧЕСКИЙ — (от гипотеза). Основанный на предположении, гадательный. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ГИПОТЕТИЧЕСКИЙ основанный на гипотезе, предположительный, гадательный, невполне достоверный. Словарь… … Словарь иностранных слов русского языка
гипотетический — гипотетичный, предположительный, проблематичный; гадательный, проблематический. Ant. очевидный, ясный, явный Словарь русских синонимов. гипотетический см. предположительный Словарь синонимов русско … Словарь синонимов
ГИПОТЕТИЧЕСКИЙ — ГИПОТЕТИЧЕСКИЙ, гипотетическая, гипотетическое (книжн.). Предположительный, основанный на гипотезе. Гипотетическое утверждение. Высказывать что нибудь гипотетически (нареч.). Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ГИПОТЕТИЧЕСКИЙ — (от греч. hypothesis – основание) условный, предположительный; суждение является гипотетическим, если действительность второго положения обусловлена действительностью первого положения: если есть А, то есть В. Философский энциклопедический… … Философская энциклопедия
гипотетический — ая, ое.hypothétique, нем. hypothetisch <лат. hypotheticus. Предположительный, возможный. Сл. 18. Низринуть идолов сект и разорить их капища до ипотетических оснований. Пнк. 1800 6. Обе оне <карты> служат к ипотетическому определению мест … Исторический словарь галлицизмов русского языка
гипотетический — гипотетический. Произносится [гипотэтический] … Словарь трудностей произношения и ударения в современном русском языке
гипотетический — [тэ], ая, ое, книжн. Основанный на гипотезе, предположительный. Гипотетическое суждение. Гипотетический случай. Родственные слова: гипотети/чески Этимология: Из западноевропейских языков (нем. hypothetisch, фр. hypothétique, англ. hypothetical… … Популярный словарь русского языка
Гипотетический — прил. 1. соотн. с сущ. гипотеза, связанный с ним 2. Свойственный гипотезе, характерный для неё. 3. Основанный на гипотезе. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
гипотетический — гипотетический, гипотетическая, гипотетическое, гипотетические, гипотетического, гипотетической, гипотетического, гипотетических, гипотетическому, гипотетической, гипотетическому, гипотетическим, гипотетический, гипотетическую, гипотетическое,… … Формы слов
гипотетический — См. ipotètico … Пятиязычный словарь лингвистических терминов
Что такое гипотетическая прогрессия
Применение понятия «прогрессия» в жизни
Автор работы награжден дипломом победителя III степени
В настоящее время актуальным вопросом становится проблема соотношения, изучаемого в школьном курсе математики, материала с жизнью. В 9 классе мы сталкиваемся с темой «Прогрессии», даем определение термину, также используем основные формулы прогрессии для решения задач. В заданиях ОГЭ используются задачи на применение основных формул прогрессий, но как эти понятия связаны с жизнью. В заданиях ЕГЭ по математике также есть задачи на применение арифметической и геометрической прогрессий, но уже с практическим содержанием.
1. Выяснить, имеют ли прогрессии практическое применение в повседневной жизни.
1. Арифметическая и геометрическая прогрессии.
1. Практическое применение прогрессий в жизни.
С целью выявления наиболее правильно ответа на наш основной вопрос «Знаете ли вы как применить свойства прогрессии в повседневной жизни?», мы провели анкетирование среди учащихся 10 – го класса и членов моей семьи.
Результаты анкетирования оказались неоднозначными. Всего было опрошено 35 человек, из них 31 % ответили на вопрос положительно, а 69 % не знают, как применять свойства прогрессии в жизни.
Также мы провели еще одно анкетирование и выяснили, что большая часть опрошенных (83 %) хотела бы узнать о необычном применении прогрессии в жизни. В связи с этим, мы считаем, что данная тема является интересной для изучения на сегодняшний день.
Определения и формулы
— это числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с постоянным для этой последовательности числом d.
Число d называется разностью прогрессии.
Любой член арифметической прогрессии вычисляется по формуле:
Сумма n первых членов арифметической прогрессии вычисляется по формуле:
— это числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности число q.
Число q называется знаменателем прогрессии.
Любой член геометрической прогрессии вычисляется по формуле:
Сумма n первых членов геометрической прогрессии вычисляется по формуле:
Зная эти формулы можно решить большое количество интересных задач: литературного, исторического и практического содержания.
Первые представления об арифметической и геометрической прогрессиях были еще у древних народов. Задачи на прогрессии, дошедшие до нас из древности, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и др.
На связь между прогрессиями первым обратил внимание великий ученый Архимед (287–212 гг. до н. э). Для нахождения площадей и объемов фигур он вывел формулу суммы квадратов натуральных чисел.
Формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом (в 3 веке).
Формула суммы членов геометрической прогрессии дана в книге Евклида “Начала” (3 век до н.э.).
Сведения, связанные с прогрессиями, впервые встречаются в дошедших до нас документах Древней Греции. Уже в V в. до н. э. греки знали следующие прогрессии и их суммы:
Известна интересная история о знаменитом немецком математике К. Гауссе (1777 – 1855), который еще в детстве проявлял выдающиеся способности к математике. Учитель предложил учащимся сложить все натуральные числа от 1 до 100. Маленький Гаусс решил эту задачу за одну минуту, сообразив, что суммы 1+100, 2+99 и т.д равны, он умножил 101 на 50, т.е. на число таких сумм. Иначе говоря, он заметил закономерность, присущую арифметическим прогрессиям.
Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен её остроумием и разнообразием возможных в ней положений. Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку. Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.
Изобретатель шахмат попросил в награду за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клетку шахматной доски положить одно зерно, на вторую – в 2 раза больше, т. е. два зерна, на третью – еще в 2 раза больше, т. е. 4 зерна и так далее до 64 – ой клетки.
Царь был удивлен, когда узнал, что такую, казалось бы, скромную просьбу невозможно выполнить.
Можно подсчитать, что масса такого числа пшеничных зерен больше триллиона тонн. Это заведомо превосходит количество пшеницы, собранной человечеством до настоящего времени.
Если бы царю удалось засеять пшеницей площадь всей поверхности Земли, считая моря, и океаны, и горы, и пустыню, и Арктику с Антарктикой, и получить удовлетворительный урожай, то, пожалуй, лет за 5 он смог бы рассчитаться.
Применение прогрессий в жизни
1. Финансовая пирамида.
Разберёмся в механизмах этих организаций.
Финансовая пирамида – способ обеспечения дохода участникам структуры за счет постоянного привлечения денежных средств. Доход первым участникам пирамиды выплачивается за счет вкладов последующих участников. В большинстве случаев истинный источник получения дохода скрывается, а декларируется вымышленный или малозначимый. Подобная подмена является мошенничеством.
Как правило, в финансовой пирамиде обещается высокая доходность, которую невозможно поддерживать длительное время, а погашение обязательств пирамиды перед всеми участниками является заведомо невыполнимым. Закономерным итогом такой ситуации является банкротство проекта и убытки последних инвесторов.
Человек собирается организовать финансовую пирамиду.
Представим, что число участников увеличивается в 5 раз с каждым кругом. В первом кругу участвуют 120 человек, во втором – 600, в третьем – 3 000, на четвертом – 15 000, на пятом – 75 000, на шестом – 375 000, на седьмом – 1 875 000, на восьмом – 9 375 000, на девятом – 46 875 000, на десятом – 234 375 000 человек.
Численность населения Воронежа составляет 1 039 801 человек (данные 2018 года). Следовательно, на седьмом кругу количество участников финансовой пирамиды превысит численность населения нашего города.
Численность населения России составляет 146 877 088 человек (данные 2018 года). Можно заметить, что на десятом кругу количество участников значительно превышает численность населения страны.
Так что участник, включившийся на седьмом или десятом круге, уже ничего не получит.
Такая закономерность чисел, также является геометрической прогрессией
2. «Сложные проценты»
В жизненной практике геометрическая прогрессия появляется в первую очередь в задаче об исчислении так называемых “сложных процентов”.
Каждому в жизни приходится решать задачи, связанные с денежными вкладами.
Применение понятия на практике
Воспользуемся конкретным примером. Размер материнского капитала составляет 453 000 р. Можно ли вложить такую сумму в банк под выгодный процент и к совершеннолетию ребенка приобрести ему квартиру?
Самый выгодный вклад, отвечающий нашим условиям, является вклад «Сохраняй» в Сбербанке России под 5 % годовых.
Первоначально вложено 453 000 р. через год сумма возрастет на 5% составит 105% от 453 000 р.
453 000 * 1, 05 (сумма составит через год)
453 000; 453 000 * 1, 05; 453 000 * 1, 05 2 ; 453 000 * 1, 05 3 ; 453 000 * 1, 05 4
Последовательность имеет вид геометрической прогрессии, где
b 1 = 453 000; g = 1, 05
453 000 * 1, 05 18 = 1, 0902 * 10 6 = 1090200 р.
Учитывая, что средняя стоимость однокомнатной квартиры в г. Воронеже составляет 1900000 р., на сумму 1090200 приобрести жилище не возможно, но подобное вложение денежных средств является достаточно выгодным.
В XIII веке в Англии ростовщики давали деньги под 50% годовых. Это вызывало страшное недовольство. Издавались законы, ограничивающие процент. Король Генрих VII даже совсем отменил взимание процентов, что привело в упадок, как банковское дело, так и промышленность, лишившуюся возможности получения кредитов. В конце концов, взимание процентов было разрешено, но не должно было быть большим 10%.
Известно, что за единицу времени такое вещество теряет определенную часть своей массы (она переходит в другое вещество и энергию). Для каждого радиоактивного вещества определяется величина T –период полураспада. Массы нераспавшегося вещества в моменты 0, T, 2T, 3T,… будут образовывать бесконечно убывающую геометрическую прогрессию.
4. Прирост древесины в лесном массиве происходит по законам геометрической прогрессии. При этом у каждой породы дерева свой коэффициент годового роста объема. Учет этих изменений позволяет планировать вырубку части лесных массивов и одновременную работу по восстановлению лесов.
5. Прогрессии в природе
Все организмы обладают интенсивностью размножения в геометрической прогрессии.
Известно, что бактерии размножаются делением: одна бактерия делится на две; каждая из этих двух в свою очередь тоже делится на две, и получаются четыре бактерии; из этих четырех в результате деления получаются восемь бактерий и т. д. (геометрическая прогрессия). Результат каждого удвоения называется поколением.
Способность к размножению у бактерий настолько велика, что если бы они не гибли от разных причин, а беспрерывно размножались, то за трое суток общая масса потомства одной только бактерии могла бы составить 7500 тонн. Таким громадным количеством бактерий можно было бы заполнить около 375 железнодорожных вагонов.
Интенсивность размножения бактерий использую в пищевой промышленности (для приготовления напитков, кисломолочных продуктов, при квашении, солении и др.), в фармацевтической промышленности (для создания лекарств, вакцин), в сельском хозяйстве (для приготовления силоса, корма для животных), в коммунальном хозяйстве и природоохранных мероприятиях (для очистки сточных вод, ликвидации нефтяных пятен).
Английский экономист епископ Мальтус использовал геометрическую и арифметическую прогрессии для оправдания войн: средства потребления (пища, одежда) растут по законам арифметической прогрессии, а люди размножаются по законам геометрической прогрессии. Мальтус считал, для того, чтобы избавиться от лишнего населения, необходимы войны.
Человек получил наследство. Первый месяц он истратил 100$, а каждый следующий месяц он тратил на 50$ больше, чем в предыдущий. Каков размер наследства, если денег хватило на год такой безбедной жизни?
9. Прогрессии в музыке
В музыке прогрессией называется постепенное повторение мотива в один или два такта в восходящем или нисходящем порядке. При таком повторении мотива выбирается интервал, на который мотив должен постоянно перестанавливаться в восходящем или нисходящем направлении. Прогрессия бывает точная или неточная. В точной, мотив повторяется на другой ступени буквально, т. е. с сохранением не только названий всех своих интервалов, но и их точной величины. В неточной прогрессии допускаются отступления от точной величины интервалов мотива, и интервала, на которой мотив перестанавливается. Прогрессия в музыке называется секвенцией.
10. Прогрессии в литературе
Даже в литературе мы встречаемся с математическими понятиями. Вспомним строки из «Евгения Онегина».
. Не мог он ямба от хорея,
Как мы не бились отличить.
«Мой дЯдя сАмых чЕстных прАвил. »
Прогрессия: 2; 4; 6; 8.
«Я пропАл, как звЕрь в загОне»
Прогрессия: 1; 3 ;5; 7.
Как вы могли заметить, исходя из вышеизложенного материала, что зная основные формулы геометрической и арифметической прогрессий, можно решить большое количество интересных задач литературного, исторического и практического содержания. Формулы и математические законы описывают явления в разных областях знаний, на первый взгляд далеких от математики.
На сегодняшний день, изучение происхождения и использования в жизни геометрической и арифметической прогрессий является актуальной и важной задачей для современных ученых.
Данное исследование позволило углубиться в изучение загадочного понятия «прогрессия», а также расширить кругозор знаний учащихся.
Вся элементарная математика. – Режим доступа: http://www.bymath.net- math 24. ru
Математический портал. – Режим доступа: http://www.webmath.ru- astro-online.ru
Ответ на поставленный
Знаете ли Вы как применить свойства прогрессии в повседневной жизни?
Арифметическая прогрессия: свойства и формулы
Определение числовой последовательности
Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.
Последовательности можно задавать разными способами:
«Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23. »
Последовательность yn = C называют постоянной или стационарной.
Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: an+1 = an + an-1.
Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.
Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.
Свойства числовых последовательностей:
Возрастающие и убывающие последовательности называют монотонными последовательностями.
Запишем числа, которые первые пришли в голову: 7, 19, 0, −1, −2, −11, 0… Сколько бы чисел не написали, всегда можно сказать, какое из них первое, какое — второе и так до последнего. То есть мы можем их пронумеровать.
Пример числовой последовательности выглядит так:
В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.
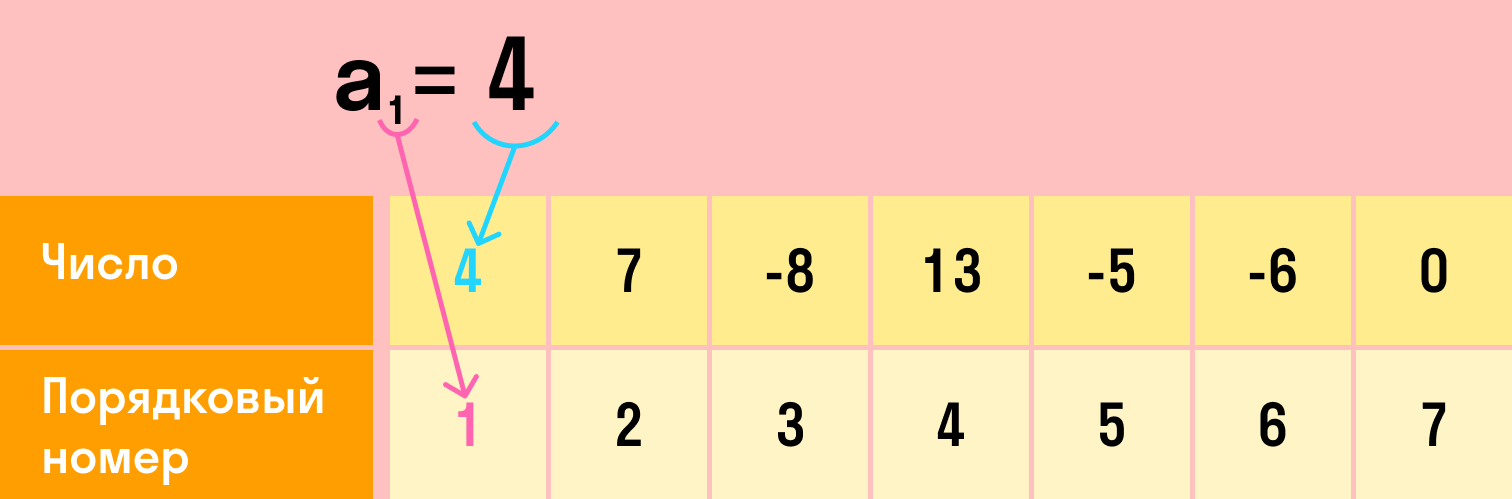
N-ный член алгебраической последовательности — это число с порядковым номером n.
Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a1, a2. a10. an.
N-ый член последовательности можно задать формулой. Например:
Определение арифметической прогрессии
Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.
Рассмотрим основные определения и как найти арифметическую прогрессию.