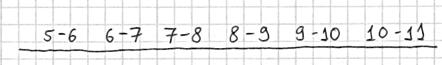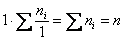Что такое гистограмма в статистике

Гистограмма

Гистограмма, это способ представления статистических данных в графическом виде – в виде столбчатой диаграммы. Она отображает распределение отдельных измерений параметров изделия или процесса. Иногда ее называют частотным распределением, так как гистограмма показывает частоту появления измеренных значений параметров объекта.

Высота каждого столбца указывает на частоту появления значений параметров в выбранном диапазоне, а количество столбцов – на число выбранных диапазонов.

Важное преимущество гистограммы заключается в том, что она позволяет наглядно представить тенденции изменения измеряемых параметров качества объекта и зрительно оценить закон их распределения. Кроме того, гистограмма дает возможность быстро определить центр, разброс и форму распределения случайной величины. Строится гистограмма, как правило, для интервального изменения значений измеряемого параметра.

Порядок построения гистограммы следующий:

1. Собираются статистические данные – результаты измерений параметра объекта. Для того, чтобы гистограмма позволяла оценить вид распределения случайной величины предпочтительно иметь не менее тридцати результатов измерений.

2. Выявляется наибольшее и наименьшее значение показателя среди полученных результатов измерений.

3. Определяется ширина диапазона значений показателя – из наибольшего значения показателя вычитается наименьшее значение.

4. Выбирается надлежащее число интервалов в пределах которых необходимо сгруппировать результаты измерений.

5. Устанавливаются границы интервалов. Границы интервалов необходимо установить так, чтобы значения данных не попадали ни на одну из границ интервала. Например, если были выбраны интервалы с границами от 0,5 до 5,5 от 5,5 до 10,5 и т.д. то значение данных 5,5 будет попадать как в первый, так и во второй интервал. Чтобы избежать этой проблемы можно изменить интервалы от 0,51 до 5,50 от 5,51 до 10,50 и так далее, таким образом ни одно значение данных не попадет на границу интервала.

6. Подсчитывается число попаданий значений результатов измерений в каждый из интервалов.

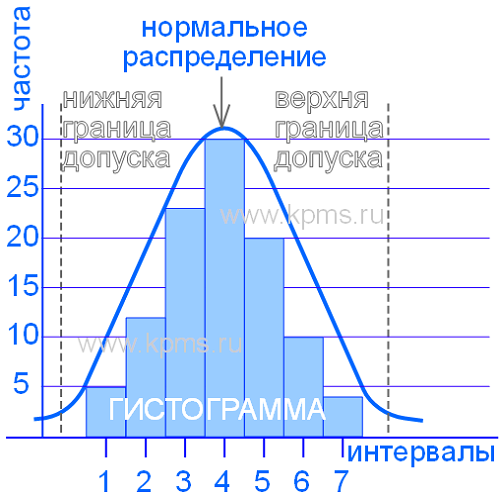
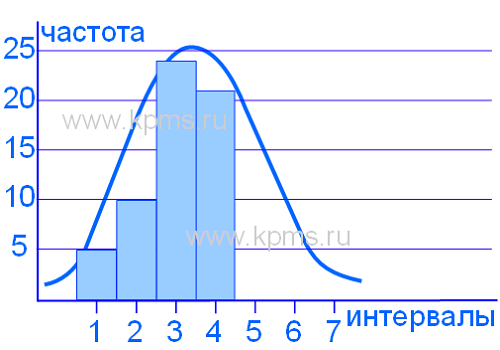
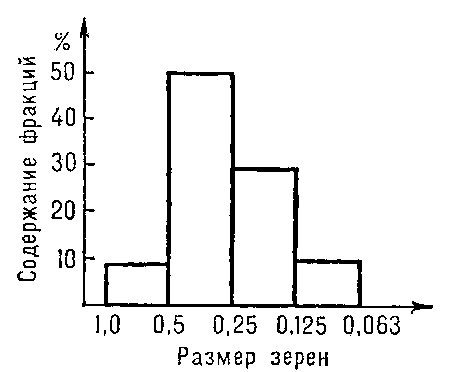
7. Строится гистограмма – на оси абсцисс (горизонтальной оси) отмечаются интервалы, а на оси ординат (вертикальной оси) отмечается частота попаданий результатов измерений в каждый интервал. Интервалы можно устанавливать в натуральных единицах (если позволяет масштаб), т.е. в тех единицах, в которых проводились измерения, либо каждому интервалу можно присвоить порядковый номер и отмечать на оси абсцисс номера интервалов. В результате получается столбчатая диаграмма, представленная на рисунке ниже.

Если на контролируемый параметр существует поле допуска, то гистограмма может содержать верхнюю и нижнюю границы поля допуска. Это позволяет увидеть в какую сторону и как смещается значение контролируемого показателя относительно поля допуска. Границы наносятся по оси абсцисс.

Гистограмма, представленная на рисунке выше имеет форму нормального распределения, что говорит о стабильности процесса, но часто бывает, что форма распределения отклоняется от нормального. Это свидетельствует о нарушениях в процессе и необходимости применения управляющих воздействий.

Некоторые, часто встречающие отклонения и их причины представлены ниже.

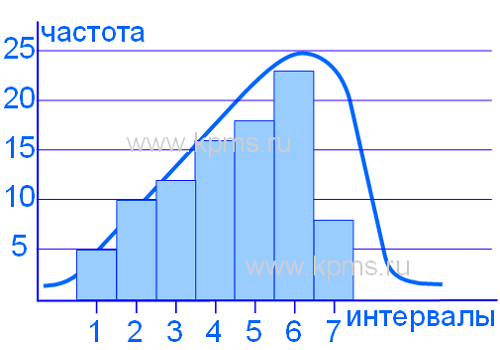
Гистограмма смещена влево (асимметрия влево):

Может вызываться смещением процесса к верхней границе допуска, либо из множества измерений отсортированы результаты, которые выпадают за пределы верхней границы допуска, либо природа процесса физически запрещает любые измерения больше чем максимальные значения допуска.

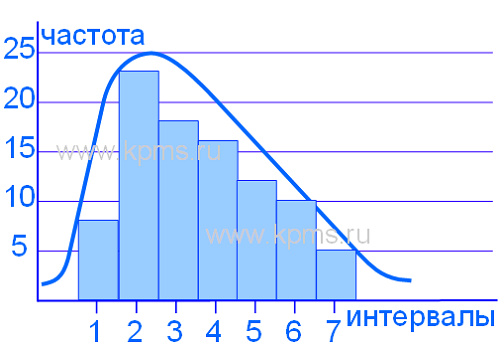
Гистограмма смещена вправо (асимметрия вправо):

Может вызываться смещением процесса к нижней границе допуска, либо из множества измерений отсортированы результаты, которые выпадают за пределы нижней границы допуска, либо природа процесса физически запрещает любые измерения меньше чем минимальные значения допуска.

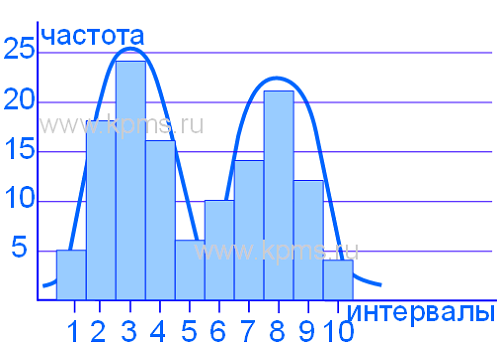
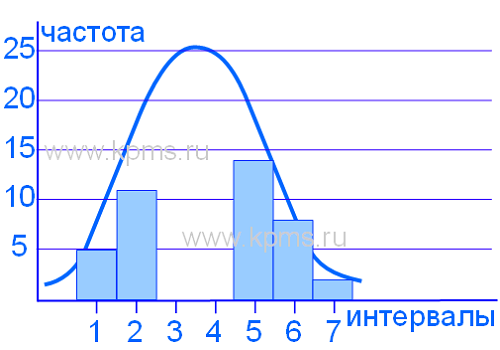
Гистограмма отображает два совмещенных процесса. Такая ситуация может произойти если результаты измерений получены от двух разных устройств, двух операторов, контролеров, разных измерительных инструментов, или с разных точек измерения.

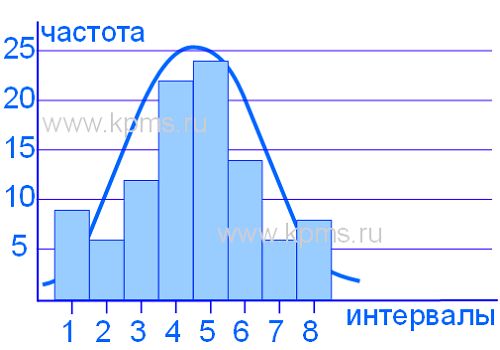
Распределение не является нормальным т.к. нет постепенного снижения частоты результатов измерений от центра к границам допуска. Такой вид гистограммы возникает если процесс не способен удовлетворять спецификациям и часть измерений отсортирована с двух сторон при приближении к границам допуска, либо потеряны чересчур малые значения результатов измерений.

Гистограмма не имеет центра:

Центр распределения был отсортирован из набора данных результатов измерений. Такая ситуация может возникнуть из-за недостаточных требований в инженерной спецификации.

Гистограмма содержит выступы на границах:

Часть измерений на удаленных от центра сторонах распределения была изменена, чтобы привести характеристики процесса в соответствие с установленным полем допуска или измерения, выходящие за пределы поля допуска были записаны как входящие в поле допуска.

Сильные стороны гистограммы, как инструмента контроля качества, заключаются в ее наглядности, простоте, возможности быстро представить вид распределения большого числа данных. Также гистограмма показывает взаимосвязь изменения контролируемых параметров по отношению к инженерным спецификациям.

К недостаткам можно отнести – отсутствие возможности количественно оценить стабильность процесса, отсутствие привязки ко времени, необходимость большого числа данных для точной оценки структуры распределения, возможность различного толкования результатов, некоторая субъективность в представлении формы распределения.

Инструмент «гистограмма» входит в состав сборника «Семь инструментов качества». Сборник можно приобрести в интернет-магазине «Менеджмент качества».

Семь инструментов качества

Семь инструментов качества

Брошюра «Семь инструментов качества» содержит справочную информацию об основных инструментах менеджмента качества. В брошюре представлено описание и даны примеры применения следующих инструментов менеджмента качества:

Источник

Гистограмма

Добавлено в закладки: 0

Что такое гистограмма? Описание и определение понятия

Гистограмма – это один из видов диаграмм, представляющий собой графическое изображение определенных статистических показателей и величин в виде столбиков. Основанием для составления диаграммы служит количественный признак. В общем виде, Гистограмма – это ряд смежных прямоугольников, выстраивающихся в ряд на прямой линии. При этом, площадь каждого из них является пропорциональной частоте, данной величине представленной в данной совокупности.

Гистограмм (от др.-греч. черта, буква, написание) — способ графического представления табличных данных.

Гистограмма в статистике

Рассмотрим более детально термин гистограмма

В большинстве статистических расчетов имеем дело либо со случайными данными, которые получены в ходе какого-либо эксперимента (выводящиеся из файла или печатаются непосредственно в документе), либо с результатами генерации случайных чисел, которые рассмотрены в предыдущих разделах встроенными функциями, которые моделируют то или иное явление методом Монте-Карло.

Гистограммой называется график, который аппроксимирует по случайным данным плотность их распределения. При построении гистограммы область значений случайной величины (а,b> разбивают на некоторое количество bin сегментов, а затем подсчитывают процент попадания данных в каждый сегмент.

Гистограмма представляет собой столбчатой график, который построен по полученным за определенный период (к примеру, за неделю или за месяц) данным, разбиваемые на несколько интервалов; число данных, которые попадают в каждый из интервалов (частота), должно выражаться высотой столбика.

Данные для построения гистограммы собирают в течение длительного периода – недели, месяца, года и т. д.

Гистограмма – это серия столбиков одинаковой ширина, но разной высота, которая показывает рассеяние и распределения данных. Ширина столбика – это интервал в диапазоне наблюдений, высотой – количество данных, которая приходится на ту или иную часть интервала, т.е. част ость. По существу, гистограмма может отображать распределение исследуемого показателя. Гистограмме позволено оценить характер рассеивания показателя и разобираться в там, на чём следует сосредотачивать усилия пo улучшению.

Как построить гистограмму?

Чтобы построить гистограмму, нарисуйте горизонтальную и вертикальную оси. Горизонтальная ось (Х) будет отображать интервалы; вертикальная ось (Y), будет отображать частоты. Нарисуйте полоску, которая представляет собой частотность данных в каждом классе. Полоски должны соприкасаться друг с другом.

Использование гистограмм

Гистограмму используют для изображения только интервальных рядов.

К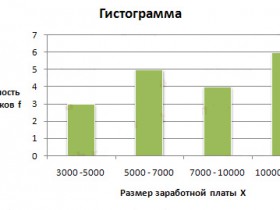оличественные соотношения некоторого показателя представлены в виде прямоугольников, площади которых пропорциональны. Чаще всего для удобства восприятия ширину прямоугольников берут одинаковую, при этом их высота определяет соотношения отображаемого параметра.

В статистике гистограмма — геометрическое изображение эмпирической функции плотности вероятности некоторой случайной величины, которое построено по выборке.

В фотографии гистограммой называют графическое представление распределения яр костей фотоснимка.

Гистограмма – это один из тех немногих способов графического представления данных, доступность и легкость восприятия которого не вызывает сомнения. Она прекрасно подходит для описания больших массивов данных, равнин как и для характеристики небольшого числового ряда.

Гистограмм называют двухмерный график, по горизонтальная ось который откладываются переменные или числовых интервалов, а по вертикальность – частота возникновения переменная (в заданном интервале). Чаще всего гистограмма составляют из прямоугольников с шириной, равной величине интервала и площадью, которая пропорциональна соответствующая частоте возникновения переменная. Другими сливами, площадь прямоугольнику соответствует количеству значения, попадающих в определенный интервал: чем большее значение, тем больше площадь – при равных значениях интервала, больший столбик будет соответствовать большему количеству значений

Мы коротко рассмотрели определение термина гистограмма, гистограмма в статистике, использование гистограмм. Оставляйте свои комментарии или дополнения к материалу.

Источник

Гистограмма

Полезное

Смотреть что такое «Гистограмма» в других словарях:

гистограмма — гистограмма … Орфографический словарь-справочник

ГИСТОГРАММА — (histogram) Диаграмма, представляющая распределение переменной величины, в том случае если имеется информация об отдельных ее значениях. Площади на диаграмме пропорциональны числу соответствующих наблюдений в каждом интервале, например ежегодных… … Экономический словарь

Гистограмма — фигура, получающаяся на плоскости, где введены декартовы координаты и по оси абсцисс отложены группированные наблюдения, а по оси ординат число соответствующих наблюдений. Верхняя часть контура Г. есть статистический аналог плотности… … Геологическая энциклопедия

Гистограмма — в техническом анализе интервальный график, на котором каждому временному интервалу ставится в соответствие отрезок прямой (палочка), начало и конец которого есть высшая и низшая цены периода. При этом цены открытия и закрытия отмечаются на… … Финансовый словарь

гистограмма — – это способ графического представления распределения числовых (непрерывных) данных, часто используемый в разведочном анализе данных для иллюстрации основных характеристик распределения. Диапазон возможных значений переменной делится на отрезки,… … Словарь социологической статистики

гистограмма — один из способов графического представления количественных данных в виде прямоугольных «столбиков», примыкающих друг к другу и соответственных частоте каждого класса данных. Словарь практического психолога. М.: АСТ, Харвест. С. Ю. Головин. 1998.… … Большая психологическая энциклопедия

гистограмма — График, состоящий из вертикальных или горизонтальных полос, высота или ширина которых пропорциональны значениям данных. [http://www.morepc.ru/dict/] гистограмма столбиковая диаграмма [Лугинский Я. Н. и др. Англо русский словарь по электротехнике… … Справочник технического переводчика

ГИСТОГРАММА — ГИСТОГРАММА, столбчатовидная диаграмма, столбцы которой представляют собой частоту (в абсолютных величинах или процент от общего), с которой определенные величины (или диапазоны величин) встречаются в пределах некоторого набора данных. см. также… … Научно-технический энциклопедический словарь

гистограмма — сущ., кол во синонимов: 1 • диаграмма (9) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

Источник

Гистограмма (статистика)

Содержание

Определение

Пусть — выборка из некоторого распределения. Определим разбиение числовой прямой

— число элементов выборки, попавших в -й интервал. Тогда кусочно-постоянная функция , имеющая вид:

Замечание

Нормализованная гистограмма является плотностью вероятности. В частности,

Гистограмма абсолютно непрерывного распределения

Пусть распределение случайных величин абсолютно непрерывно, и задаётся плотностью вероятности . Тогда

по вероятности при .

Замечание

Таким образом площадь фигуры под нормализованной гистограммой, ограниченной интервалом , приближается к вероятности принятия значений внутри этого интервала любой из случайных величин . Однако, нормализованная гистограмма не сходится поточечно к теоретической плотности распределения этих случайных величин.

См. также

Полезное

Смотреть что такое «Гистограмма (статистика)» в других словарях:

Гистограмма (значения) — Гистограмма: Гистограмма способ графического представления табличных данных. Гистограмма (статистика) это функция, приближающая плотность вероятности некоторого распределения, построенная на основе выборки из него. Гистограмма (фотография) это… … Википедия

Гистограмма — Пример гистограммы У этого термина существуют и другие значения, см. Гистограмма (значения). Гистограмма (от др. греч … Википедия

Статистика — Гистограмма (метод графических изображений) У этого термина существуют и другие значения, с … Википедия

Математическая статистика — раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов. При этом статистическими данными называются сведения о числе объектов в какой либо… … Большая советская энциклопедия

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА — раздел математики, посвященный математич. методам систематизации, обработки и использования статистич. данных для научных и практич. выводов. При этом статистич. данными наз. сведения о числе объектов в какой либо более или менее обширной… … Математическая энциклопедия

Вариация (статистика) — У этого термина существуют и другие значения, см. Вариация. Вариация различие значений какого либо признака у разных единиц совокупности за один и тот же промежуток времени. Причиной возникновения вариации являются различные условия… … Википедия

ВАРИАЦИОННАЯ СТАТИСТИКА — ВАРИАЦИОННАЯ СТАТИСТИКА, термин, объединяющий группу приемов статистического анализа, применяющихся преимущественно в естественных науках. Во второй половине XIX в. Кетле (Quetelet, «Anthro pometrie ou mesure des differentes facultes de 1… … Большая медицинская энциклопедия

Математическая статистика — Математическая статистика наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на … Википедия

Правовая статистика — Правовая статистика система концепций и методов общей теории статистики, применяемых к области изучения правонарушений и мер социального контроля над ними. Правовая статистика является одной из отраслей статистической науки, которая своими… … Википедия

Описательная статистика — Цель описательной (дескриптивной) статистики обработка эмпирических данных, их систематизация, наглядное представление в форме графиков и таблиц, а также их количественное описание посредством основных статистических показателей. В отличие от… … Википедия

Источник

3. Интервальный вариационный ряд.
Гистограмма относительных частот

На предыдущем уроке по математической статистике (Занятие 1) мы разобрали дискретный вариационный ряд (Занятие 2), и сейчас на очереди интервальный. Его понятие, графическое представление (гистограмма и эмпирическая функция распределения), а также рациональные методы вычислений, как ручные, так и программные. В том числе будут рассмотрены задачи с достаточно большим количеством (100-200) вариант – что делать в таких случаях, как обработать большой массив данных.

Предпосылкой построения интервального вариационного ряда (ИВР) является тот факт, что исследуемая величина принимает слишком много различных значений. Зачастую ИВР появляется в результате измерения непрерывной характеристики изучаемых объектов. Типично – это время, масса, размеры и другие физические характеристики. Подходящие примеры встретились в первой же статье по матстату, вспоминаем Константина, который замерял время на лабораторной работе и Фёдора, который взвешивал помидоры.

Для изучения интервального вариационного ряда затруднительно либо невозможно применить тот же подход, что и для дискретного ряда. Это связано с тем, что ВСЕ варианты многих ИВР различны. И даже если встречаются совпадающие значения, например, 50 грамм и 50 грамм, то связано это с округлением, ибо полученные значения всё равно отличаются хоть какими-то микрограммами.

Поэтому для исследования ИВР используется другой подход, а именно, определяется интервал, в пределах которого варьируются значения, затем данный интервал делится на частичные интервалы, и по каждому интервалу подсчитываются частоты – количество вариант, которые в него попали.

Разберём всю кухню на конкретной задаче, и чтобы как-то разнообразить физику, я приведу пример с экономическим содержанием, кои десятками предлагают студентам экономических отделений. Деньги, строго говоря, дискретны, но если надо, непрерывны :), и по причине слишком большого разброса цен, для них целесообразно строить интервальный ряд:

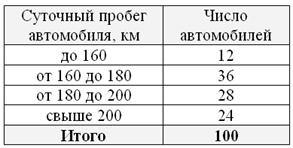
По результатам исследования цены некоторого товара в различных торговых точках города, получены следующие данные (в некоторых денежных единицах):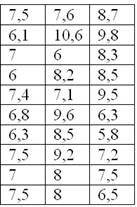

Требуется составить вариационный ряд распределения, построить гистограмму частот, гистограмму и полигон относительных частот + бонус – эмпирическую функцию распределения.

Такое обывательское исследование проводит каждый из нас, начиная с анализа цены на пакет молока вот это дожил в нескольких магазинах, и заканчивая ценами на недвижимость по гораздо бОльшей выборке. Что называется, не какие-то там унылые сантиметры.

Поэтому представьте свой любимый товар / услугу и наслаждайтесь решением🙂

Очевидно, что перед нами выборочная совокупность объемом 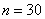наблюдений (таблица 10*3), и вопрос номер один: какой ряд составлять – дискретный или интервальный? Смотрим на таблицу: среди предложенных цен есть одинаковые, но их разброс довольно велик, и поэтому здесь целесообразно провести интервальное разбиение. К тому же цены могут быть округлёнными.

Начнём с экстремальной ситуации, когда у вас под рукой нет Экселя или другого подходящего программного обеспечения. Только ручка, карандаш, тетрадь и калькулятор.

Тактика действий похожа на исследование дискретного вариационного ряда. Сначала окидываем взглядом предложенные числа и определяем примерный интервал, в который вписываются эти значения. «Навскидку» все значения заключены в пределах от 5 до 11. Далее делим этот интервал на удобные подынтервалы, в данном случае напрашиваются промежутки единичной длины. Записываем их на черновик:

Теперь начинаем вычёркивать числа из исходного списка и записывать их в соответствующие колонки нашей импровизированной таблицы: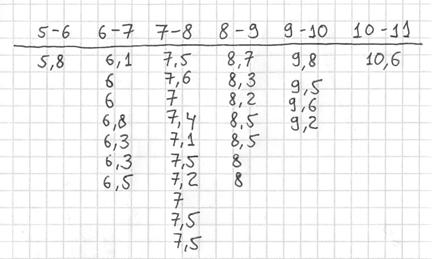

После этого находим самое маленькое число в левой колонке и самое большое значение – в правой. Тут даже ничего искать не пришлось, честное слово, не нарочно получилось:)
ден. ед. – хорошим тоном считается указывать размерность.

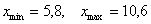
Вычислим размах вариации:
ден. ед. – длина общего интервала, в пределах которого варьируется цена.

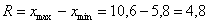
Теперь его нужно разбить на частичные интервалы. Сколько интервалов рассмотреть? По умолчанию на этот счёт существует формула Стерджеса:

, где – десятичный логарифм* от объёма выборки и – оптимальное количество интервалов, при этом результат округляют до ближайшего левого целого значения.

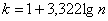
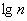
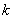
* есть на любом более или менее приличном калькуляторе

В нашем случае получаем:
интервалов.

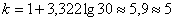
Следует отметить, что правило Стерджеса носит рекомендательный, но не обязательный характер. Нередко в условии задачи прямо сказано, на какое количество интервалов нужно проводить разбиение (на 4, 5, 6, 10 и т.д.), и тогда следует придерживаться именно этого указания.

Длины частичных интервалов могут быть различны, но в большинстве случаев использует равноинтервальную группировку:
– длина частичного интервала. В принципе, здесь можно было не округлять и использовать длину 0,96, но удобнее, ясен день, 1.

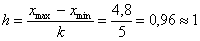
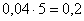
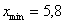
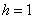
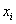
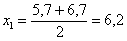
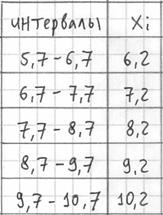
И коль скоро мы прибавили 0,04, то по 5 частичным интервалам у нас получается «перебор»: . Посему от самой малой варианты отмеряем влево 0,1 влево (половину «перебора») и к значению 5,7 начинаем прибавлять по , получая тем самым частичные интервалы. При этом сразу рассчитываем их середины (например, ) – они требуются почти во всех тематических задачах:

– убеждаемся в том, что самая большая варианта 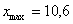вписалась в последний частичный интервал и отстоит от его правого конца на 0,1.

Далее подсчитываем частоты по каждому интервалу. Для этого в черновой «таблице» обводим значения, попавшие в тот или иной интервал, подсчитываем их количество и вычёркиваем: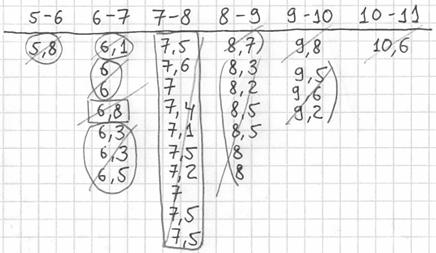

Так, значения из 1-го интервала я обвёл овалами (7 штук) и вычеркнул, значения из 2-го интервала – прямоугольниками (11 штук) и вычеркнул и так далее.

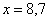
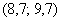
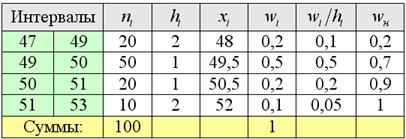
Правило: если варианта попадает на «стык» интервалов, то её следует относить в правый интервал. У нас такая варианта встретилась одна: – и её нужно причислить к интервалу .

В результате получаем интервальный вариационный ряд:

при этом обязательно убеждаемся в том, что ничего не потеряно: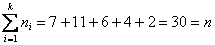
, ОК.

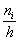
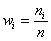
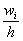
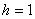
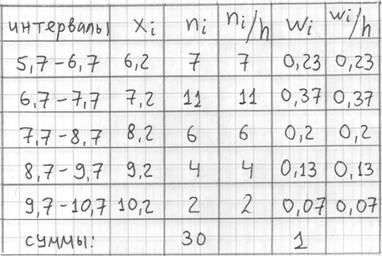
Изобразим ряд графически. Для этого по каждому интервалу нужно найти (не пугаемся): плотность частот , относительные частоты (округляем их до 2 знаков после запятой), а также плотность относительных частот . Поскольку длина частичного интервала , то вычисления заметно упрощаются:

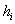
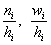
В том случае, если интервалы имеют разные длины , то при нахождении плотностей каждую частоту нужно делить на длину своего интервала: . Но у нас популярная равноинтервальная группировка, да не абы какая, а с единичным частичным интервалом. Возьмите на заметку всю выгоду такого интервала.

Дело за чертежами. Один за другим.

Гистограмма частот – это фигура, состоящая из прямоугольников, ширина которых равна длинам частичных интервалов, а высота – соответствующим плотностям частот: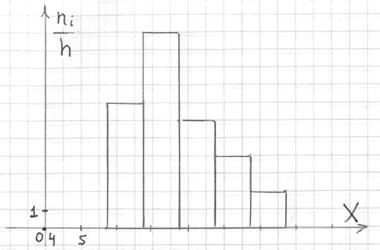

При этом вполне допустимо использовать нестандартную шкалу по оси абсцисс, в данном случае я начал нумерацию с четырёх.

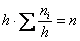
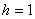
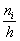
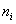
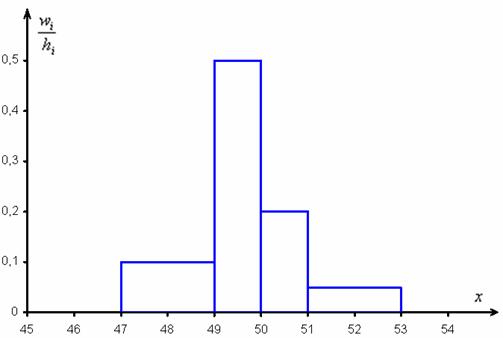
Площадь гистограммы частот в точности равна объёму совокупности: . В нашем случае и плотности совпали с самими частотами , таким образом:

Гистограмма относительных частот – это фигура, состоящая из прямоугольников, ширина которых равна длинам частичных интервалов, а высота – соответствующим плотностям относительных частот: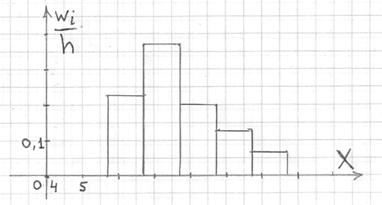

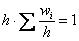
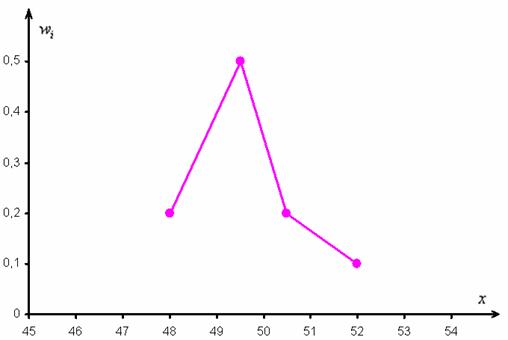
Площадь такой гистограммы равна единице: , и это статистический аналог функции плотности распределения непрерывной случайной величины. Построенный чертёж даёт наглядное и весьма точное представление о распределении цен на ботинки по всей генеральной совокупности. Но это при условии, что выборка представительна.

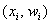
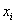
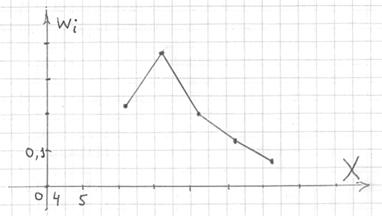
И для ИВР чаще всего строят гистограмму именно относительных частот. А вместе с ней нередко и полигон таковых частот. Без проблем, полигон относительных частот – это ломаная, соединяющая соседние точки , где – середины интервалов:

По сути, здесь мы приблизили интервальный ряд дискретным, выбрав в качестве вариант 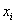середины интервалов. Это важнейший принцип и метод, который неоднократно встретится нам в последующих задачах.

Автоматизируем решение в Экселе:

Как составить ИВР и представить его графически? (Ютуб)

(видео с неточностями, скоро исправлю и перезалью)

И бонус – эмпирическая функция распределения. Она определяется точно так же, как в дискретном случае:

, где – количество вариант СТРОГО МЕНЬШИХ, чем «икс», который «пробегает» все значения от «минус» до «плюс» бесконечности.

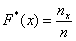
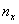
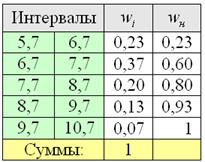
Но вот построить её для интервального ряда намного проще. Находим накопленные относительные частоты:

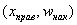
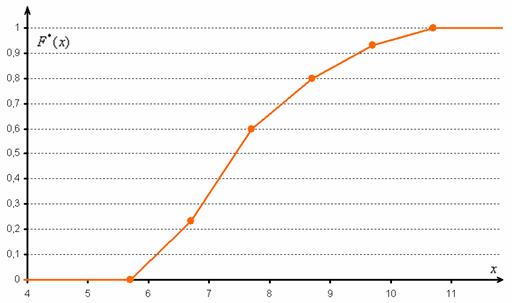
И строим кусочно-ломаную линию, с промежуточными точками , где – правые концы интервалов, а – относительная частота, которая успела накопиться на всех «пройденных» интервалах:

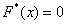
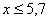
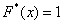
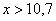
При этом если и если .

Напоминаю, что данная функция не убывает, принимает значения из промежутка 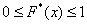и, кроме того, для ИВР она ещё и непрерывна.

Эмпирическая функция распределения является аналогом функции распределения НСВ и приближает теоретическую функцию 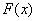, которую теоретически, а иногда и практически можно построить по всей генеральной совокупности.

Помимо перечисленных графиков, вариационные ряды также можно представить с помощью кумуляты и огивы частот либо относительных частот, но в классическом учебном курсе эта дичь редкая, и поэтому о ней буквально пару абзацев:

Кумулята – это ломаная, соединяющая точки:

* либо – для дискретного вариационного ряда;
либо – для интервального вариационного ряда.

* – накопленные «обычные» частоты

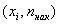
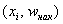
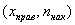
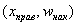
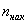
В последнем случае кумулята относительных частот 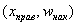представляет собой «главный кусок» недавно построенной эмпирической функции распределения.

Огива – это обратная функция по отношению к кумуляте – здесь варианты откладываются по оси ординат, а накопленные частоты либо относительные частоты – по оси абсцисс.

С построением данных линий, думаю, проблем быть не должно, чего не скажешь о другой проблеме. Хорошо, если в вашей задаче всего лишь 20-30-50 вариант, но что делать, если их 100-200 и больше? В моей практике встречались десятки таких задач, и ручной подсчёт здесь уже не торт. Считаю нужным снять небольшое видео:

Как быстро составить ИВР при большом объёме выборки? (Ютуб)

Ну, теперь вы монстры 8-го уровня 🙂

Но не всё так сурово. В большинстве задач вам предложат готовый вариационный ряд, и на счёт молока, то, конечно, была шутка:

Выборочная проверка партии чая, поступившего в торговую сеть, дала следующие результаты:

Требуется построить гистограмму и полигон относительных частот, эмпирическую функцию распределения

Проверяем свои навыки работы в Экселе! (исходные числа и краткая инструкция прилагается) И на всякий случай краткое решение для сверки в конце урока. Должен признаться, я немного усложнил это задание, сделав интервалы разной длины – для лучшего понимания материала.

Что ещё важного по теме? Время от времени встречаются ИВР с открытыми крайними интервалами, например:

В таких случаях, что убийственно логично, интервалы «закрывают». Обычно поступают так: сначала смотрим на средние интервалы и выясняем длину частичного интервала: 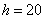км. И для дальнейшего решения можно считать, что крайние интервалы имеют такую же длину: от 140 до 160 и от 200 до 220 км. Тоже логично. Но уже не убийственно:) Если внутренние интервалы имеют разные длины, то для крайних интервалов можно взять среднюю арифметическую известных длин.

Ну вот, пожалуй, и вся практически важная информация по ИВР.

На очереди числовые характеристики вариационных рядов и начнём мы с их центральных характеристик, а именно – Моды, медианы и средней.

Пример 7. Решение: в данной задаче интервалы имеют разные длины 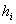, заполним расчётную таблицу:

Построим гистограмму относительных частот:

Построим полигон относительных частот:

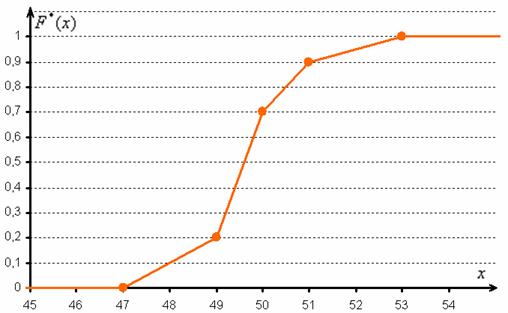
Построим эмпирическую функцию распределения:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник