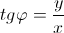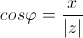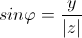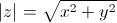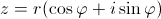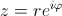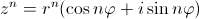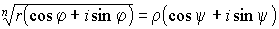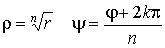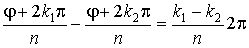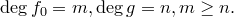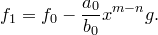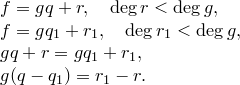Что такое главное значение аргумента комплексного числа
Что такое главное значение аргумента комплексного числа
где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для мнимой единицы
Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Числа z = x + iy и 
Алгебраической формой комплексного числа называется з апись числа z в виде z = x + iy.
Модуль r и аргумент φ можно рассматривать как полярные координаты вектора 
Равенство (7.3) есть тригонометрическая форма комплексного числа. Модуль r = |z| однозначно определяется по формуле
Аргумент определяется из формул:
Используя формулу Эйлера
комплексное число 
где r =| z | — модуль комплексного числа, а угол 
Пример 7.1. Записать комплексные числа 
На множестве комплексны х чисел определен ряд операций.
Из (7.11) следует важнейшее соотношение i 2 = –1. Действительно,
Видно, что при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. Нетрудно видеть, что если есть n множителей и все они одинаковые, то частным случаем равенства (7.12) является формула возведения комплексного числа в натуральную степень:
(7.13) называется первой формулой Муавра.
Произведение двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
На практике при нахождении частного двух комплексных чисел удобно умножить числитель и знаменатель дроби 
Деление комплексных чисел осуществляется также и в тригонометрической форме, при этом имеет место формула:
Видно, что при делении комплексных чисел их модули делятся, а аргументы вычитаются соответственно.
Частное двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
Пользуясь формулой (7.11), вычислим их произведение
На основании формулы (7.14) вычислим их частное
Решение. Используя (7.4) и (7.5), получаем:
Аналогично, для z 2 можно записать:
По формулам (7.12) и (7.16) получим в тригонометрической форме:
Пользуясь формулами (7.14) и (7.17), получим в показательной форме:
в натуральную степень, определенному ранее формулой (7.13).
(7.18) называется второй формулой Муавра.
Пример 7.4. Найти все корни уравнения z 4 +16=0.
Теорема 7.1 (основная теорема алгебры). Для всякого многочлена с комплексными коэффициентами
Приведем еще одну теорему, имеющую место над множеством комплексных чисел.
Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.
Модуль и аргумент комплексного числа
Пример №1 Найти модуль и аргумент числа и представить число в тригонометрической и показательной формах.
, поэтому прибавляем 

Кроме алгебраической формы записи комплексного числа имеются тригонометрическая и показательная формы записи. Модуль и аргумент числа 

а в показательной форме:
При переходе от показательной форме к тригонометрической используется формула Эйлера:
Зачем нужны три формы записи? Дело в том, что некоторые действия удобно производить с конкретно одной формой. Например, сложение удобно проводить с числами в алгебраической форме и неудобно с числами в двух других формах. Умножение и деление очень хорошо получается с числами в показательной и тригонометрической формах. Но одно важно: чтобы произвести арифметическое действие с комплексными числами нужно перевести их в одну форму. Приведем несколько примеров.
Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.
Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.
Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.
Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).
В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.
В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.
Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.
Нужна помощь с курсовой или дипломной работой?
Комплексные числа
Формы
Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:
Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.
Изображение
Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:
Вычислить сумму и разность заданных комплексных чисел:
Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел:
Аналогично выполним вычитание чисел:
Выполнить умножение и деление комплексных чисел:
Так, теперь разделим первое число на второе:
Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки:
Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы:
Для возведения в квадрат достаточно умножить число само на себя:
Пользуемся формулой для умножения, раскрываем скобки и приводим подобные:
В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую.
Вычисляем значение модуля:
Найдем чем равен аргумент:
$$ \varphi = arctg \frac<3> <3>= arctg(1) = \frac<\pi> <4>$$
Записываем в тригонометрическом виде:
Преобразуем в алгебраическую форму для наглядности:
Представим число в тригонометрической форме. Найдем модуль и аргумент:
Используем знакомую формулу Муавра для вычисления корней любой степени:
Модуль и аргумент комплексного числа, их свойства. Тригонометрическая форма записи числа. Формула муравла.
Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки, соответствующей данному комплексному числу и обозначается Arg(z) = φ
Из определения следуют следующие формулы:
Для числа z = 0 аргумент не определен.
Главным значением аргумента называется такое значение φ, что 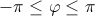
| 1. | 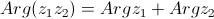 | — аргумент от произведения двух комплексных чисел равен сумме аргументов этих чисел |
| 2. | 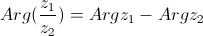 | — аргумент частного двух комплексных чисел равен разности аргументов этих чисел |
| 3. | 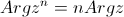 | |
| 4. | 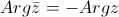 | — аргумент от сопряженного к комлексного числа равен отрицательному значению аргумента от этого числа. |
Модулем комплексного числа z = x + iy называется вещественное число |z| равное:
Для любых комплексных числе z, z1, z2 имеют место следубщие свойства модуля:
| 1. | 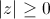 , причем |z| = 0 тогда и только тогда, когда z = 0 , причем |z| = 0 тогда и только тогда, когда z = 0 |
| 2. | 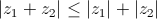 — неравенство треугольника для комплексных чисел — неравенство треугольника для комплексных чисел |
| 3. |  |
| 4. |  |
| 5. | для пары комплексных чисел z1 и z2 модуль их разности |z1 − z2| равен расстоянию между соответствующими точками комплексной плоскости |
ригонометрическая форма записи комплексного числа:
Показательная форма записи комплексного числа:
Для тригонометрической формы записи верны следующие свойства:
| 1. |  |
| 2. |  |
| 3. |  |
Для показательной формы записи справедливы следующие свойства:
| 1. |  |
| 2. |  |
| 3. |  |
| 4. | 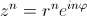 |
| 5. |  |
5. Извлечение корня n-степени из комплексного числа?
Корнем n-й степени из комплексного числа называется такое комплексное число, n-я степень которого равна подкоренному числу.
Таким образом, равенство:
Но у равных комплексных чисел модули должны быть равны, и аргументы могут отличаться лишь кратным 2p, т.е.
 | (16) |
т.е. для извлечения корня из комплексного числа надо извлечь корень из его модуля, а аргумент разделить на показатель корня.
В формуле (16) число k может принимать всевозможные целые значения; однако можно показать, что различных значений корня будет только n, и они будут соответствовать значениям:

т.е. значению k2 соответствует то же значение корня, что и значению k1, заключающемуся в ряде (17). Итак, корень n-й степени из комплексного числа имеет n различных значений.
Исключение из этого правила представляет лишь частный случай, когда подкоренное число равно нулю, т.е. r = 0. В этом случае все указанные выше значения корня равны нулю.
6.Многочлены. Деление многочленов с остатком?
Многочлены применяются во многих разделах, в том числе рассмотрении нуля, отрицательных и комплексных чисел, теории групп, колец, узлов, множеств и т.д. Использование полиномиальных вычислений значительно упрощает выражение свойств разных объектов.
Основные определения многочлена:
• Каждое слагаемое полинома называется одночленом или мономом.
• Многочлен, состоящий из двух одночленов, называют двучленом или биномом.
• Коэффициенты полинома – вещественные или комплексные числа.
• Если старший коэффициент равен 1, то многочлен называют унитарным (приведенным).
• Степени переменной в каждом одночлене – целые неотрицательные числа, максимальная степень определяет степень многочлена, а его полной степенью называется целое число, равное сумме всех степеней.
• Одночлен, соответствующий нулевой степени, называется свободным членом.
• Многочлен, все одночлены которого имеют одинаковую полную степень, называется однородным.
Определение. Пусть 
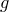


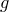





Полином 

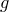

Пример. 

Теорема. (о делении с остатком). Пусть 
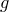







Доказательство. Существование.
Пусть 
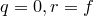

Предположим, что теорема верна не для любого полинома 
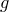

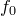
Пусть 
Коэффициент при 







Получили противоречие с тем предположением, что есть многочлены, для которых теорема неверна.
Единственность. Предположим, что
1) 

2) 

Получили противоречие. Этот случай невозможен.