Что такое глубина модуляции

Коэффициент амплитудной модуляции

Коэффицие́нт амплиту́дной модуля́ции (коэффициент АМ, устар. глубина модуляции) — основная характеристика амплитудной модуляции — отношение разности между максимальным и минимальным значениями амплитуд модулированного сигнала к сумме этих значений, выраженное в процентах . На практике часто применяют также понятия «коэффициент АМ вверх» и «коэффициент АМ вниз», означающие максимальные отклонения мгновенной амплитуды сигнала соответственно в большую и меньшую стороны от среднего значения.

Содержание

Измерения

См. также

Ссылки

Литература

Полезное

Смотреть что такое «Коэффициент амплитудной модуляции» в других словарях:

коэффициент амплитудной модуляции — Ндп. коэффициент глубины модуляции Отношение разности между максимальным и минимальным значениями амплитуд модулированного сигнала к сумме этих значений, выраженное в процентах. [ГОСТ 24375 80] Недопустимые, нерекомендуемые коэффициент глубины… … Справочник технического переводчика

коэффициент амплитудной модуляции — [IEV number 314 08 04] EN amplitude modulation factor ratio, for amplitude modulation, of half the difference of the maximum and minimum amplitudes to the mean value of the amplitude NOTE – This definition does not apply to asymmetrical… … Справочник технического переводчика

Коэффициент амплитудной модуляции — 145. Коэффициент амплитудной модуляции Ндп. Коэффициент глубины модуляции Источник: ГОСТ 24375 80: Радиосвязь. Термины и определения оригинал документа Смотри также родственные термины: 35. Коэффициент амплитудной модуляции напряжения Коэффи … Словарь-справочник терминов нормативно-технической документации

коэффициент амплитудной модуляции — amplitudės moduliavimo faktorius statusas T sritis Standartizacija ir metrologija apibrėžtis Moduliuotojo virpesio didžiausiosios ir mažiausiosios amplitudės pusinio skirtumo ir amplitudės vidutinės vertės dalmuo. atitikmenys: angl. amplitude… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

коэффициент амплитудной модуляции — amplitudės moduliavimo faktorius statusas T sritis fizika atitikmenys: angl. amplitude modulation factor vok. Amplitudenmodulationsfaktor, m; Amplitudenmodulationsgrad, m rus. коэффициент амплитудной модуляции, m pranc. taux de modulation… … Fizikos terminų žodynas

Коэффициент амплитудной модуляции — 1. Отношение разности между максимальным и минимальным значениями амплитуд модулированного сигнала к сумме этих значений, выраженное в процентах Употребляется в документе: ГОСТ 24375 80 2. Отношение разности между максимальным и минимальным… … Телекоммуникационный словарь

коэффициент амплитудной модуляции напряжения — Коэффициент, характеризующий колебания напряжения и равный отношению полуразности наибольшей и наименьшей амплитуд модулированного напряжения, взятых за определенный интервал времени, к номинальному или базовому значению напряжения. [ГОСТ 23875… … Справочник технического переводчика

Коэффициент амплитудной модуляции напряжения — 35. Коэффициент амплитудной модуляции напряжения Коэффициент, характеризующий колебания напряжения и равный отношению полуразности наибольшей и наименьшей амплитуд модулированного напряжения, взятых за определенный интервал времени, к… … Словарь-справочник терминов нормативно-технической документации

коэффициент амплитудной модуляции напряжения К_АМ — 106 коэффициент амплитудной модуляции напряжения КАМ: Коэффициент, характеризующий колебания напряжения и равный отношению полуразности наибольшей и наименьшей амплитуд модулированного напряжения, взятых за определенный интервал времени, к… … Словарь-справочник терминов нормативно-технической документации

Коэффициент — (от лат. co(cum) «совместно» и лат. efficients «производящий») числовой множитель при буквенном выражении, известный множитель при той или иной степени неизвестного, или постоянный множитель при переменной величине.… … Википедия

Источник

Теория радиоволн: аналоговая модуляция

Амплитудная модуляция

При амплитудной модуляции, огибающая амплитуд несущего колебания изменяется по закону, совпадающему с законом передаваемого сообщения. Частота и фаза несущего колебания при этом не меняется.

Одним из основных параметров АМ, является коэфициент модуляции(M).
Коэффициент модуляции — это отношение разности между максимальным и минимальным значениями амплитуд модулированного сигнала к сумме этих значений(%).
Проще говоря, этот коэффициент показывает, насколько сильно значение амплитуда несущего колебания в данный момент отклоняется от среднего значения.
При коэффициенте модуляции больше 1, возникает эффект перемодуляции, в результате чего происходит искажение сигнала.

Данный спектр свойственен для модулирующего колебания постоянной частоты.

На графике, по оси Х представлена частота, по оси У — амплитуда.
Для АМ, кроме амплитуды основной частоты, находящейся в центре, представлены также значения амплитуд справа и слева от частоты несущей. Это так называемые левая и правая боковые полосы. Они отнесены от частоты несущей на расстояние равное частоте модуляции.
Расстояние от левой до правой боковой полосы называют ширина спектра.
В нормальном случае, при коэффициенте модуляции

Источник

Что такое глубина модуляции

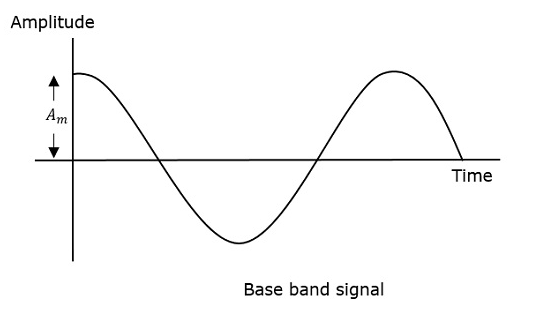
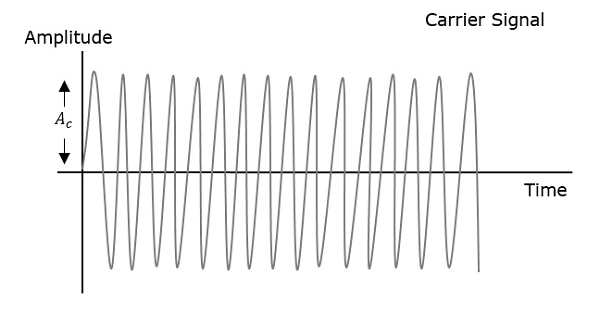
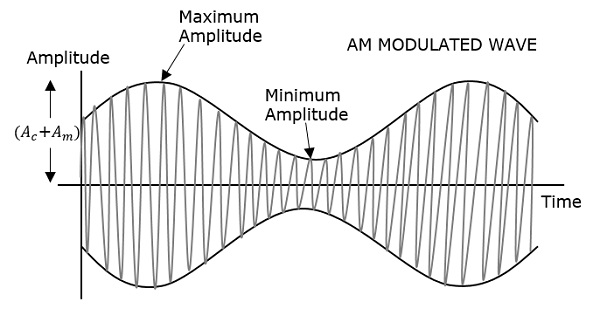
Амплитудная модуляция (AM) — наиболее распространенный тип модуляции. В системе с AM амплитуда несущей изменяется в соответствии с изменением сигнала или информации (рис. 14.1). В отсутствие сигнала амплитуда несущей имеет постоянный уровень, как показано на рис. 14.1(б). При модуляции синусоидальным сигналом амплитуда несущей увеличивается или уменьшается относительно своего немодулированного уровня по синусоидальному закону в соответствии с нарастанием или спаданием модулирующего сигнала. Чем больше амплитуда модулирующего сигнала, тем сильнее изменяется амплитуда несущей. Амплитудно-модулированная несущая (рис. 14.1(в)) имеет огибающую, в точности повторяющую форму модулирующего сигнала, и при демодуляции именно эта огибающая выделяется как полезный сигнал.

Глубина модуляции

Отношение амплитуды модулирующего сигнала к амплитуде несущей называется глубиной или коэффициентом модуляции. Она определяет меру изменения уровня несущей при модуляции. Глубина модуляции всегда выражается в процентах, и поэтому о ней говорят как о «процентной» модуляции.
Амплитуда сигнала
Глубина модуляции = ——————————— • 100%
Амплитуда несущей

(см. рис. 14.1). Например, если амплитуда сигнала равна 1 В, а амплитуда несущей — 2 В, то глубина модуляции составляет (1 В)/(2 В) • 100% = 50%. Такую глубину модуляции имеет АМ-несущая, показанная на рис. 14.1.

Рис. 14.1. Амплитудная модуляция (глубина модуляции 50%);
(а) сигнал; (б) несущая; (в) модулированная несущая.

Перемодуляция

На рис. 14.2(а) показана АМ-несущая со 100%-ной глубиной модуляции. Глубина модуляции, превышающая 100%, приводит к искажениям (рис. 14.2(б)). По этой причине глубину модуляции ограничивают. Например, при передачах радиостанции Би-би-си она ограничена величиной 80%.

Рис. 14.2. (а) Модуляция 100%; (б) перемодуляция.

Боковые частоты

Можно показать, что амплитудно-модулированная несущая состоит из трех гармонических (синусоидальных) компонент с постоянными амплитудами и разными частотами. Этими тремя компонентами являются: сама несущая и два сигнала боковых частот f1 и f2. Каждый модулирующий гармонический сигнал порождает две боковые частоты. Пусть fs – частота модулирующего сигнала и fc – частота несущей, тогда

f1 = fc – fs, f2 = fc + fs,

где f1 и f2 – так называемые нижняя боковая и верхняя боковая частоты соответственно. Например, если частота несущей равна 100 кГц, а частота сигнала — 1 кГц, то

Нижняя боковая частота f1 = 100 – 1 = 99 кГц,
Верхняя боковая частота f2 = 100 + 1 = 101 кГц.
Амплитудно-модулированная несущая, т. е. несущая вместе с двумя сигналами боковых частот, может быть представлена в виде трех вертикальных стрелок, каждая из которых соответствует одному гармоническому сигналу (рис. 14.3). То, что изображено на этом рисунке, называется частотным спектром сигнала (в данном случае частотным спектром АМ-несущей).

Рис. 14.3. Частотный спектр AM-несущей. Рис. 14.4. Боковые полосы.

Боковые полосы

Информационные сигналы почти всегда имеют сложную форму и состоят из большого числа гармонических сигналов. Поскольку каждый гармонический сигнал порождает пару боковых частот, то сложный негармонический сигнал будет порождать многочисленные боковые частоты, что приведет к образованию двух полос частот по обе стороны от несущей (рис. 14.4). Это так называемые боковые полосы частот. Область частот между наибольшей верхней боковой частотой f2 и наименьшей верхней боковой частотой f4 называют верхней боковой полосой (ВБП). Аналогично область частот между наибольшей нижней боковой частотой f3 и наименьшей нижней боковой частотой f1 называют нижней боковой полосой (НБП).
Эти две боковые полосы расположены симметрично относительно несущей, и каждая из них содержит одну и ту же информацию. Несущая не несет никакой информации. Всю информацию несут боковые частоты.
При модуляции одиночным гармоническим сигналом принимается, что верхняя и нижняя боковые полосы простираются от несущей до верхней и нижней боковых частот соответственно (рис. 14.5).

Пример 1

Несущая с частотой 100 кГц промодулирована по амплитуде сигналом, занимающим полосу частот 400-3400 Гц. Определите ширину боковых полос.

Решение

Частота 400 Гц, самая низкая в спектре сигнала, порождает еще две боковые частоты:

Ширина полосы частот

Другими словами, в данном случае ширина полосы частот, занимаемой амплитудно-модулированной несущей, равна удвоенной частоте модулирующего сигнала.
В случае передачи сложного сигнала ширина полосы частот, занимаемой АМ-системой передачи информации, равна удвоенной наивысшей частоте в спектре модулирующего сигнала и, таким образом, включает в себя все боковые частоты.

Одно- и двухполосная передача

Поскольку одна боковая полоса содержит столько же информации, сколько и другая, передачу можно осуществлять с использованием только одной боковой полосы, и при этом не будет никакой потери информации. При однополосной передаче (SSB — по связной терминологии) одна из боковых полос — или нижняя, или верхняя — подавляется и передается только одна оставшаяся боковая полоса. При двухполосной (DSB) передаче передаются обе боковые полосы.
Однополосная передача занимает лишь половину той полосы частот, которая используется при двухполосной передаче, и по этой причине она применяется в телефонии и радиосвязи. При однополосной передаче в заданном диапазоне частот несущей можно расположить вдвое большее число информационных каналов, чем при двухполосной передаче. В силу простоты двухполосная передача используется всеми радиовещательными системами с AM. Поэтому, когда речь идет о связи с использованием AM, обычно имеется в виду двухполосная передача, если не оговорено обратное.

Пример 2

Несущая промодулирована по амплитуде периодическим сигналом в виде меандра с частотой 100 Гц. Пренебрегая гармониками выше пятой, установите ширину полосы частот, необходимую а) для DSB (двухполосной)-передачи и б) для SSB (однополосной)-передачи.

Решение

Сигнал в виде меандра с частотой 100 Гц содержит следующие гармоники:

основную гармонику =100 Гц,
гармонику 3-го порядка = 3 • 100 = 300 Гц,
гармонику 5-го порядка = 5 • 100 = 500 Гц.

Гармониками более высокого порядка пренебрегаем. Таким образом, в обрезанном спектре модулирующего сигнала максимальная частота fмакс = 500 Гц.
Ширина полосы для DSB-передачи = 2 • fмакс = 2•500 = 1000 Гц.
Ширина полосы для SSB-передачи = DSB/2 = 1000/2 = 500 Гц.

В этом видео рассказывается об амплитудной модуляции:

Источник

Амплитудная модуляция

Непрерывная волна идет непрерывно без каких-либо интервалов, и это сигнал сообщения основной полосы частот, который содержит информацию. Эта волна должна быть модулирована.

Согласно стандартному определению, «амплитуда несущего сигнала изменяется в соответствии с мгновенной амплитудой модулирующего сигнала». Это означает, что амплитуда несущего сигнала, который не содержит никакой информации, изменяется в соответствии с амплитудой сигнала на каждом мгновенный, который содержит информацию. Это можно хорошо объяснить следующими рисунками.

Модулирующая волна, которая показана первой, является сигналом сообщения. Следующей является несущая волна, которая является высокочастотным сигналом и не содержит никакой информации. В то время как последний является результирующей модулированной волной.

Математическое выражение

Ниже приведены математические выражения для этих волн.

Представление волн во временной области

Пусть модулирующий сигнал будет —

m ( t ) = A m c o s ( 2 p i f m t )

Пусть сигнал несущей будет —

c ( t ) = A c c o s ( 2 p i f c t )

Где A _m = максимальная амплитуда модулирующего сигнала

A _c = максимальная амплитуда несущего сигнала

Стандартная форма амплитудно-модулированной волны определяется как —

S ( t ) = A c [ 1 + K a m ( t ) ] c o s ( 2 p i f c t )

S ( t ) = A c [ 1 + m u c o s ( 2 p i f m t ) ] c o s ( 2 p i f c t )

Индекс модуляции

Источник

Амплитудная модуляция

u(t) = U(t) Ч cos( w o t+ j o ), (9.1.1)

U(t) = U m Ч [1+M Ч s(t)], (9.1.2)

где U m – постоянная амплитуда несущего колебания при отсутствии входного (модулирующего) сигнала s(t), М – коэффициент амплитудной модуляции

Рис. 9.1.1. Модулированный сигнал. Рис. 9.1.2. Глубокая модуляция

Стопроцентная модуляция (М=1) может приводить к искажениям сигналов при перегрузках передатчика, если последний имеет ограниченный динамический диапазон по амплитуде несущих частот или ограниченную мощность передатчика (увеличение амплитуды несущих колебаний в пиковых интервалах сигнала U(t) в два раза требует увеличения мощности передатчика в четыре раза).

Рис. 9.1.3. Перемодуляция сигнала. Рис. 9.1.4. Физические спектры сигналов.

Однотональная модуляция

u(t) = U m [1+M Ч cos( W t)] Ч cos( w o t). (9.1.3)

Значения начальных фазовых углов несущего и модулирующего колебания здесь и в дальнейшем, если это не имеет принципиального значения, для упрощения получаемых выражений будем принимать равными нулю. С учетом формулы cos(x) Ч cos(y) = (1/2)[cos(x+y)+cos(x-y)] из выражения (9.1.3) получаем:

Энергия однотонального АМ-сигнала

Энергия однотонального АМ-сигнала. Обозначим раздельными индексами (нес- несущая, вб- верхняя боковая, нб- нижняя боковая) составляющие колебания однотонального АМ-сигнала (9.1.4) и определим функцию его мгновенной мощности:

u(t) = u нес (t) + u вб (t) + u нб (t).

p(t)=u 2 (t)= u 2 нес (t)+u 2 вб (t)+u 2 нб (t)+2u нес (t)u вб (t)+2u нес (t)u нб (t)+2u вб (t)u нб (t). (9.1.5)

Для определения средней мощности сигнала выполним усреднение функции p(t):

P u =

Все взаимные мощности модулированного сигнала при усреднении становятся равными нулю (спектры не перекрываются), при этом:

P u = Р нес + Р вб + Р нб = U m 2 /2 + (U m M) 2 /4. (9.1.6)

Доля мощности боковых частот в единицах мощности несущей частоты:

(Р вб + Р нб ) / Р нес = М 2 /2, (9.1.7)

т.е. не превышает 50% даже при 100%-ной модуляции.

Под полезной мощностью модулированных сигналов понимают мощность, несущую информацию, т.е. в данном случае мощность боковых частот. Коэффициент полезного действия данного типа модуляции определяется отношением мощности боковых частот к общей средней мощности модулированного сигнала:

h АМ = (U m 2 M 2 /4) / P u = M 2 / (М 2 +2). (9.1.8)

Как можно видеть на рис. 9.1.5, даже при М=1 КПД амплитудной модуляции составляет только 33%, а при практическом использовании обычно меньше 20%.

Многотональный модулирующий сигнал

Многотональный модулирующий сигнал имеет произвольный спектральный состав. Математическая модель такого сигнала, в том числе непрерывного по частоте, может быть аппроксимирована тригонометрической суммой, в пределе бесконечной:

s(t) =a n cos( W n t+ F n ), (9.1.9)

u(t) = U m [1+ М n cos( W n t+ F n )] Ч cos( w o t+ j o ). (9.1.10)

u(t) = U m cos( w o t+ j o ) + (U m /2) M n cos[( w o + W n )t +j o +F n ] +

Частотный диапазон каротажного кабеля длиной 1 км 0-200 кГц. Частотный диапазон измерительных датчиков скважинного прибора 5-5000 Гц. От какого количества датчиков одновременно может передаваться информация по данному каротажному кабелю?

Минимальная несущая частота должна быть на порядок выше максимальной частоты модулирующего сигнала, т.е. порядка 50 кГц. Для передачи сигнала от одного датчика требуется полоса частот 2 Ч 5 = 10 кГц плюс пустой защитный интервал для исключения перекрестных помех порядка 1 кГц, т.е. 11 кГц. Общее количество каналов передачи информации: (200-50+5)/11 = 14 каналов.

Автокорреляционная функция АМ-сигналов

Автокорреляционная функция АМ-сигналов:

B u ( t ) =u(t) u(t- t ) dt. (9.1.12)

C учетом того, что постоянная фаза не влияет на форму АКФ, при u(t)=U(t)·cos w o t получаем:

cos w o t · cos w o (t- t ) = 0.5 cos w o t + 0.5 cos w o ( 2t- t ).

B u ( t ) =U(t) U(t- t ) dt + 0.5U(t) U(t- t ) cos w o ( 2t- t ) dt. (9.1.13)

B u ( t ) @ B U ( t ). (9.1.14)

Полная энергия сигнала за счет усреднения по высокочастотным колебаниям:

При бесконечной энергии сигнала:

B u ( t ) =. (9.1.15)

Демодуляция АМ-сигналов

Демодуляция АМ-сигналов может выполняться несколькими способами.

Самый простейший способ – двухполупериодное детектирование (вычисление модуля сигнала) с последующим сглаживанием полученных однополярных полупериодов несущей фильтром низких частот.

На рис. 9.1.7 приведен пример изменения однотонального амплитдно-модулированного сигнала и его физического спектра при детектировании (в реальной односторонней шкале частот и в реальной шкале амплитудных значений гармоник колебаний). Параметры представленного сигнала: несущая частота 30 Гц, частота модуляции 3 Гц, коэффициент модуляции М=1.

Как видно на рисунке, при детектировании спектр модулированного сигнала становится однополярным, переходит на основную несущую частоту 2 w o и уменьшается по энергии почти в 5 раз. Основная часть энергии (более 4/5) трансформируется в область низких частот и распределяется между постоянной составляющей и выделенной гармоникой сигнала модуляции. Между постоянной составляющей и выделенной гармоникой энергия распределяется в зависимости от значения коэффициента модуляции М. При М=1 энергии равны, при М=0 (в отсутствие сигнала модуляции) вся энергия переходит на постоянную составляющую.

Рис. 9.1.7. Изменение однотонального модулированного сигнала при детектировании

Кроме этих составляющих в спектре появляются также 2-я, 3-я и более высокие гармоники детектированного модулированного сигнала (т.е. в данном случае на частотах <117, 120, 123>Гц, <177, 180, 183>Гц и т.д.), которые не показаны на рисунке. Энергия второй гармоники не превышает 2%, а остальных и вовсе незначительна. Демодуляторы сигнала выделяют после детектирования только низкочастотный информационный сигнал и подавляют все остальные частоты, включая постоянную составляющую.

Очевидно также, что в случае перемодуляции сигнала исходный информационный сигнал будет восстанавливаться с ошибкой.

y(t) = u(t) cos( w o t) = U(t) cos( w o t) cos( w o t) = Ѕ U(t) + Ѕ U(t) cos(2 w o t). (9.1.16)

Однако при синхронном детектировании требуется точное совпадение фаз и частот опорного колебания демодулятора и несущей гармоники АМ-сигнала.

При сдвиге фазы опорного колебания на Dw относительно несущей частоты выходной сигнал демодулятора оказывается умноженным на косинус фазовой ошибки:

y(t) = U(t) cos( w o t) cos( w o t- Dj ) = Ѕ U(t) cos(- Dj ) + Ѕ U(t) cos(2 w o t- Dj ).

и амплитуда сигнала занижается, а при Dw = p /2 становится равной нулю.

При сдвиге частоты между несущим и опорным колебаниями сигнал демодулятора оказывается умноженным на гармоническое колебание с разностной частотой:

Для частотной и фазовой синхронизации между несущим и опорным колебаниями в составе демодуляторов обычно используются следящие системы фазовой автоподстройки опорной частоты.

Балансная амплитудная модуляция или АМ с подавлением несущей частоты (АМ-ПН)

Как следует из вышеприведенных данных, основная доля мощности АМ – сигнала приходится на несущую частоту. При балансной модуляции производится перемножение двух сигналов – модулирующего и несущего, при котором происходит подавление несущего колебания, соответственно, КПД модуляции становится равным 100%. Так, для однотонального сигнала (без учета начальных фаз колебаний) при U(t) = M Ч cos( W t) имеем:

Однако балансная модуляция не получила широкого распространения в связи с трудностями, возникающими при демодуляции сигналов. В принципе, синхронное детектирование, как и для АМ, позволяет выполнять демодуляцию без каких-либо проблем, но при условии известной частоты несущей сигнала и точной фазовой синхронизации опорной частоты с несущей. Но во входном сигнале демодулятора при АМ-ПН несущая частота отсутствует, и автоматическая синхронизация становится невозможной. Для снятия этой трудности обычно применяют неполное подавление несущей и оставляют в модулированном сигнале определенный «остаток» несущей (пилот-сигнал), который и используется для фазочастотной автосинхронизации при демодуляции.

Однополосная амплитудная модуляция

u(t) = U m cos( w o t+ j o ) + (U m /2) M n cos[( w o ± W n )t +j o ±F n ]. (9.1.19)

Рис. 9.1.10. Однополосная амплитудная модуляция.

Внешняя форма ОБП – сигнала после удаления одной боковой полосы, пример которой приведен на рис. 9.1.10 для однотонального сигнала, сходна с обычным АМ – сигналом, но ее огибающая, как это нетрудно заметить, отличается от огибающей U(t), заданной при модуляции по при М = 1 (показана пунктиром).

Для демодуляции ОБП – сигнала может использоваться как двухполупериодное, так и синхронное детектирование, со всеми особенностями, присущими этим методам. Результаты демодуляции отличаются от демодуляции АМ – сигналов только в 2 раза меньшей амплитудой выходных сигналов.

При однополосной модуляции возможно также подавление несущей частоты (полное или частичное, с оставлением пилот-сигнала), что позволяет полнее использовать мощность передатчика.

Полярная модуляция

Полярная модуляция решает конкретную техническую задачу – передачу двух сигналов одновременно, что требуется, например, в стереовещании или при передаче стереоснимков. Рассмотрим это на примере стереосигналов.

В системе стереовещания необходимо передавать два сигнала s 1 (t) и s 2 (t) одновременно (левый и правый каналы) при условии совмещения с монофоническими приемниками. Для выполнения этого условия создается специальный модулирующий сигнал. Процесс создания сигнала поясняется на рис. 9.1.11, где в качестве канальных сигналов приняты моногармонические сигналы s1 и s2.

Рис. 9.1.11. Полярная модуляция.

что позволяет восстанавливать исходные сигналы каналов:

Монофонический сигнал является основным и не изменяется по частоте, что позволяет принимать его монофоническим приемникам. Для одновременной передачи разностного сигнала монофонический сигнал суммируется с поднесущей частотой w o (subcarrier), которая располагается за звуковым диапазоном частот монофонических приемников (в области ультразвука), и модулируется разностным сигналом (с установкой коэффициента модуляции значением смещения А о ):

s(t) = s mono (t) + (A o + s diff (t))·cos( w o t).

Релятивисты и позитивисты утверждают, что «мысленный эксперимент» весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.

Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.

Источник