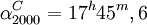Что такое горизонтальная система координат и для чего ее ввели

Горизонтальная система небесных координат в навигации

Принципы горизонтальной системы небесных координат и примеры навигационных расчетов.

Горизонтальная система небесных координат – навигационная система для авиационного и морского транспорта, в которой положение светила на небесной сфере ориентируют относительно истинного горизонта. Если проще, то в горизонтальной системе небесных координат за основную плоскость принимается плоскость истинного горизонта, а полюсами, соответственно, являются зенит и надир (самая верхняя и с самая нижняя точки) небесной сферы.

Положение светила в горизонтальной системе координат определяется азимутом и высотой светила.

Общая схема принципа действия горизонтальной системы небесных координат

Принцип горизонтальной системы небесных координат

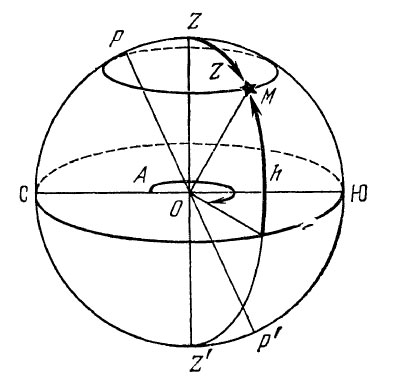
Азимутом светила А называется двугранный угол в плоскости истинного горизонта, заключенный между плоскостью небесного меридиана и плоскостью вертикала светила. Азимут отсчитывается от северного направления небесного меридиана по ходу часовой стрелки от 0 до 360°. Светила, находящиеся на одном вертикале, имеют одинаковые азимуты.

Положение светила на вертикале определяется другой координатой —высотой. Высотой светила h называется угол между плоскостью истинного горизонта и направлением на светило из центра небесной сферы. Высоту можно измерять также дугой вертикала от плоскости истинного горизонта до альмукантарата светила. Высота измеряется от 0 до ±90°.
Положительные высоты светила отсчитываются к зениту, а отрицательные к надиру, т. е. светила, находящиеся над горизонтом, имеют положительную высоту, а находящиеся под горизонтом — отрицательную. Вместо высоты светила иногда пользуются другой координатой — зенитным расстоянием.

Зенитным расстоянием Z называется угол в плоскости вертикала, заключенный между вертикалью наблюдателя и направлением на светило из центра небесной сферы. Зенитное расстояние отсчитывается от точки зенита до направления на светило от 0 до 180°.

Между высотой и зенитным расстоянием светила существует следующая зависимость:

h+Z = 90°, откуда Z = 90° — h; h = 90° — Z.

Светила, находящиеся на одном альмукантарате, имеют одинаковые высоты и одинаковые зенитные расстояния.

Особенности горизонтальной системы небесных координат

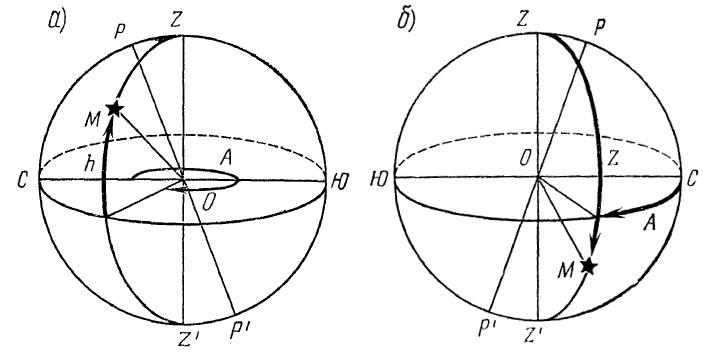
Горизонтальные координаты светил непрерывно и неравномерно изменяются вследствие суточного вращения Земли. Они изменяются также и с переменой места наблюдателя. Однако горизонтальные координаты удобны тем, что их можно непосредственно измерить с помощью специальных приборов и по ним легко можно представить положение светила на небесной сфере. Ниже приведены примеры графического изображения положения светил на небесной сфере по за-данным горизонтальным координатам.

Иллюстрация принципа определения координат объекта с помощью горизонтальной системы небесных координат (к примерам 1 и 2 выше)

источник: по книге “Авиационная астрономия”

Источник

Рис. 6. Горизонтальная система координат

Горизонтальная система координат

В горизонтальной системе координат основной плоскостью является плоскость истинного горизонта местности, а полюсами — зенит и надир.
Плоскости, содержащие линию «зенит – надир» и потому проходящие через центр небесной сферы, называются вертикалами. Вертикал, проходящий через точки востока и запада, и тем самым перпендикулярный плоскости небесного меридиана, называется первым вертикалом.
Определяющими параметрами в горизонтальной системе координат являются азимут и высота небесного объекта над горизонтом.
Высота (h) отсчитывается от плоскости горизонта: в видимой небесной полусфере со знаком «плюс», а в невидимой небесной полусфере — со знаком «минус». Как и географическая широта, аналогом которой она в какой-то мере является, высота измеряется в пределах от +90° до –90°.
Вместо высоты h иногда используют зенитное расстояние z, величина которого определяется соотношением: z = 90° – h. Геометрически зенитное расстояние представляет собой угол между направлением на точку зенита (вертикальной осью) и направлением на небесный объект. Величина z всегда положительна и может принимать значение в пределах от 0° (в точке зенита) до 180° (в точке надира).
Азимут (А) представляет собой двугранный угол между плоскостью нулевого небесного меридиана и плоскостью вертикала и аналогичен географической долготе. Азимут отсчитывается от направления на юг по ходу часовой стрелки и измеряется в пределах от 0° до 360°.

Источник

Системы небесных координат

Системы небесных координат используются в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение объектов на небесной сфере. Таким образом, системы небесных координат являются сферическими системами координат, в которых третья координата — расстояние — часто неизвестна и не играет роли. Эти системы отличаются друг от друга выбором основной плоскости и началом отсчёта.

В зависимости от стоя́щей задачи, может быть более удобным использовать ту или иную систему. Наиболее часто используются горизонтальная и экваториальные системы координат. Реже — эклиптическая, галактическая и другие.

Содержание

Горизонтальная система координат

В этой системе основной плоскостью является плоскость математического горизонта. Одной координатой при этом является либо высота светила h, либо его зенитное расстояние z. Другой координатой является азимут A.

Высотой h светила называется дуга вертикального круга от математического горизонта до светила, или угол между плоскостью математического горизонта и направлением на светило. Высоты отсчитываются в пределах от 0° до +90° к зениту и от 0° до −90° к надиру.

Зенитным расстоянием z светила называется дуга вертикального круга от зенита до светила, или угол между отвесной линией и направлением на светило. Зенитные расстояния отсчитываются в пределах от 0° до 180° от зенита к надиру.

Азимутом A светила называется дуга математического горизонта от точки юга до вертикального круга светила, или угол между полуденной линией и линией пересечения плоскости математического горизонта с плоскостью вертикального круга светила. Азимуты отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от точки юга, в пределах от 0° до 360°. Иногда азимуты отсчитываются от 0° до +180° к западу и от 0° до −180° к востоку. (В геодезии азимуты отсчитываются от точки севера.)

Первая экваториальная система координат

В этой системе основной плоскостью является плоскость небесного экватора. Одной координатой при этом является склонение δ (реже — полярное расстояние p). Другой координатой — часовой угол t.

Склонением δ светила называется дуга круга склонения от небесного экватора до светила, или угол между плоскостью небесного экватора и направлением на светило. Склонения отсчитываются в пределах от 0° до +90° к северному полюсу мира и от 0° до −90° к южному полюсу мира.

Полярным расстоянием p светила называется дуга круга склонения от северного полюса мира до светила, или угол между осью мира и направлением на светило. Полярные расстояния отсчитываются в пределах от 0° до 180° от северного полюса мира к южному.

Часовым углом t светила называется дуга небесного экватора от верхней точки небесного экватора (то есть точки пересечения небесного экватора с небесным меридианом) до круга склонения светила, или двугранный угол между плоскостями небесного меридиана и круга склонения светила. Часовые углы отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от верхней точки небесного экватора, в пределах от 0° до 360° (в градусной мере) или от 0 h до 24 h (в часовой мере). Иногда часовые углы отсчитываются от 0° до +180° (от 0 h до +12 h ) к западу и от 0° до −180° (от 0 h до −12 h ) к востоку.

Вторая экваториальная система координат

В этой системе, как и в первой экваториальной, основной плоскостью является плоскость небесного экватора, а одной координатой — склонение β (реже — полярное расстояние p). Другой координатой является прямое восхождение α.

Прямым восхождением (RA,α) светила называется дуга небесного экватора от точки весеннего равноденствия до круга склонения светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга склонения светила. Прямые восхождения отсчитываются в сторону, противоположную суточному вращению небесной сферы, в пределах от 0° до 360° (в градусной мере) или от 0 h до 24 h (в часовой мере).

RA — астрономический эквивалент земной долготы. И RA и долгота измеряют угол восток-запад вдоль экватора; обе меры берут отсчёт от нулевого пункта на экваторе. Для долготы, нулевой пункт — нулевой меридиан; для RA нулевой отметкой является место на небе, где Солнце пересекает небесный экватор в весеннее равноденствие.

Склонение (δ) в астрономии — одна из двух координат экваториальной системы координат. Равняется угловому расстоянию на небесной сфере от плоскости небесного экватора до светила и обычно выражается в градусах, минутах и секундах дуги. Склонение положительно к северу от небесного экватора и отрицательно к югу.

У склонения всегда указывается знак, даже если склонение положительно.

Склонение небесного объекта, проходящего через зенит, равно широте наблюдателя (если считать северную широту со знаком +, а южную отрицательной). В северном полушарии Земли для заданной широты φ небесные объекты со склонением δ > 90° − φ не заходят за горизонт, поэтому называются незаходящими. Если же склонение объекта δ [1]

Эклиптическая система координат

В этой системе основной плоскостью является плоскость эклиптики. Одной координатой при этом является эклиптическая широта β, а другой — эклиптическая долгота λ.

Эклиптической широтой β светила называется дуга круга широты от эклиптики до светила, или угол между плоскостью эклиптики и направлением на светило. Эклиптические широты отсчитываются в пределах от 0° до +90° к северному полюсу эклиптики и от 0° до −90° к южному полюсу эклиптики.

Эклиптической долготой λ светила называется дуга эклиптики от точки весеннего равноденствия до круга широты светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга широты светила. Эклиптические долготы отсчитываются в сторону видимого годового движения Солнца по эклиптике, то есть к востоку от точки весеннего равноденствия в пределах от 0° до 360°.

Галактическая система координат

В этой системе основной плоскостью является плоскость нашей Галактики. Одной координатой при этом является галактическая широта b, а другой — галактическая долгота l.

Галактической широтой b светила называется дуга круга галактической широты от эклиптики до светила, или угол между плоскостью галактического экватора и направлением на светило.

Галактические широты отсчитываются в пределах от 0° до +90° к северному галактическому полюсу и от 0° до −90° к южному галактическому полюсу.

Галактической долготой l светила называется дуга галактического экватора от точки начала отсчёта C до круга галактической широты светила, или угол между направлением на точку начала отсчёта C и плоскостью круга галактической широты светила. Галактические долготы отсчитываются против часовой стрелки, если смотреть с северного галактического полюса, то есть к востоку от точки начала отсчёта C в пределах от 0° до 360°.

Точка начала отсчёта C находится вблизи направления на галактический центр, но не совпадает с ним, поскольку последний, вследствие небольшой приподнятости Солнечной системы над плоскостью галактического диска, лежит примерно на 1° к югу от галактического экватора. Точку начала отсчёта C выбирают таким образом, чтобы точка пересечения галактического и небесного экваторов с прямым восхождением 280° имела галактическую долготу 32,93192° (на эпоху 2000).

Координаты точки начала отсчёта C на эпоху 2000 в экваториальной системе координат составляют:

Изменения координат при вращении небесной сферы

Высота h, зенитное расстояние z, азимут A и часовой угол t светил постоянно изменяются вследствие вращения небесной сферы, так как отсчитываются от точек, не связанных с этим вращением. Склонение δ, полярное расстояние p и прямое восхождение α светил при вращении небесной сферы не изменяются, но они могут меняться из-за движений светил, не связанных с суточным вращением.

История и применение

Небесные координаты употреблялись уже в глубокой древности. Описание некоторых систем содержится в трудах древнегреческого геометра Евклида (около 300 до н. э.). Опубликованный в «Альмагесте» Птолемея звёздный каталог Гиппарха содержит положения 1022 звёзд в эклиптической системе небесных координат.

Наблюдения изменений небесных координат привели к величайшим открытиям в астрономии, которые имеют огромное значение для познания Вселенной. К ним относятся явления прецессии, нутации, аберрации, параллакса, собственных движений звёзд и другие. Небесные координаты позволяют решать задачу измерения времени, определять географические координаты различных мест земной поверхности. Широкое применение находят небесные координаты при составлении различных звёздных каталогов, при изучении истинных движений небесных тел — как естественных, так и искусственных — в небесной механике и астродинамике и при изучении пространственного распределения звёзд в проблемах звёздной астрономии.

Использование различных систем координат

Горизонтальная система координат используется для определения направления на светило с помощью угломерных инструментов и при наблюдениях в телескоп, смонтированный на азимутальной установке.

Первая экваториальная система координат используется для определения точного времени и при наблюдениях в телескоп, смонтированный на экваториальной установке.

Вторая экваториальная система координат является общепринятой в астрометрии. В этой системе составляются звёздные карты и описываются положения светил в каталогах.

Эклиптическая система координат используется в теоретической астрономии при определении орбит небесных тел.

Источник

Что такое горизонтальная система координат и для чего ее ввели

Простейшей системой координат является горизонтальная система. Она определяется плоскостью горизонта и одной из точек пересечения этой плоскости с большим кругом (см. разд. 2.9.1), проходящим через северный полюс мира и зенит. Начало горизонтальной системы координат совпадает с наблюдателем, так что эта система является сугубо локальной.

Как показано на рис: 2.2, точка зенита лежит на продолженной вверх линии отвеса. Надир находится в противоположном направлении. Удобной абстракцией является предположение, что Земля окружена огромной сферой произвольного радиуса, на внутреннюю поверхность которой проектируются звезды и другие небесные

тела. Эта сфера называется небесной сферой. Поскольку в астрономии расстояния до тел нас часто не интересуют, то радиус сферы можно выбирать произвольным и его часто берут равным единице.

Северный и южный полюсы мира — это точки пересечения оси вращения Земли с небесной сферой. Наблюдателю в северном полушарии кажется, что северный полюс мира — это точка, вокруг которой вращается небесный свод, делая один оборот за 24 ч. В настоящее время яркая Полярная звезда находится на расстоянии менее одного градуса от северного полюса мира.

Однако вследствие прецессии (см. разд. 3.4) она постепенно уходит от полюса, возвращаясь в его окрестность примерно через каждые 26 000 лет.

На рис. 2.3 показана небесная сфера, в центре которой находится наблюдатель. Здесь Z — зенит, О — наблюдатель, Р — северный полюс мира, ОХ — мгновенное направление на небесное тело. Большой круг, проведенный через Z и Р, пересекает горизонт NESAW в точках севера N и юга S. Другой большой круг WZE, составляющий прямой угол с большим кругом NPZS, пересекает горизонт в точках запада № и востока Е. Дуги ZN, ZW, ZA и т. д. называются вертикалами, точки N, Е, S и W называются главными точками.

Положение объекта X в такой системе координат задается двумя углами — азимутом А и высотой а. Азимут может определяться разными способами. Поэтому каждый раз, имея дело с такой системой, надо решать, каким определением следует воспользоваться.

Например, азимут может определяться как угол между вертикалами, проходящими через точку юга и объект X. Этот угол измеряется вдоль горизонта в западном направлении от 0 до 360°. Азимут может определяться и как угол между вертикалами, проходящими через точку севера и объект X, и измеряться вдоль горизонта в западном или восточном направлении от 0 до 180°. Обычно используется третье определение: азимут отсчитывается от точки севера в сторону востока от 0 до 360°.

В данной книге принято именно такое определение, которое фактически аналогично определению направления по часовой стрелке.

Если наблюдатель находится в южном полушарии, то азимут измеряется от точки юга в восточном направлении от 0 до 360°.

Высота а точки X — это угол, измеряемый вдоль вертикального круга, проходящего через X, от точки А горизонта до X. Он измеряется в градусах. Вместо высоты можно использовать и другую координату — зенитное расстояние (ZX на рис. 2.3), которое также измеряется в градусах. Очевидно, имеет место соотношение

Основной недостаток горизонтальной системы координат связан с тем, что она локальная. Два наблюдателя, расположенные в различных точках на поверхности Земли, будут в один и тот же момент

времени получать различные значения высоты и азимута для одной и той же звезды. Кроме того, поскольку, с точки зрения наблюдателя, небесная сфера вращается, то координаты звезды со временем будут изменяться. Однако и в настоящее время многие наблюдения проводятся в такой, как ее часто называют, альтазимутальной системе. Например, 250-футовый радиотелескоп в Джод-релл-Бэнк (Великобритания) имеет альтазимутальную монтировку. При этолг для преобразования горизонтальных координат в экваториальные и наоборот используется специальная ЭВМ.

Источник

Урок 8. Системы небесных координат

Урок 8. Системы небесных координат

Тема. Системы небесных координат.

Учащиеся должны знать:

1. определение, единицы измерения, пределы измерения горизонтальных координат: высоты, зенитного расстояния, азимута. Взаимосвязь высоты и зенитного расстояния;

2. определение, единицы измерения, пределы измерения экваториальных координат: склонения, прямого восхождения;

3. вывод формулы высоты светила в верхней кульминации.

4. Учащиеся должны уметь применять полученные знания при решении качественных задач

Основные понятия. Прямое восхождение, склонение, высота светила, азимут, зенитное расстояние.

Демонстрационный материал. ИИСС «Планетарий». Иллюстрации.

Самостоятельная деятельность учащихся. Выполнение заданий с помощью электронного планетария.

Мировоззренческий аспект урока. Формирование научного подхода к изучению мира.

Использование новых информационных технологий. Работа с интерактивным электронным планетарием.

Краткое содержание урока

1. Актуализация знаний.

2. Изучение нового материала

3. Закрепление материала.

Объяснение учителя, беседа

4. Самостоятельная работа с планетарием и подвижной картой.

6. Домашнее задание

Запись на доске учителя

Чтобы определить, будет ли видно то или иное светило в определенный момент времени и в какой именно области неба, необходимо ввести систему координат, связанную с истинным горизонтом. Такая система координат называется горизонтальной.

Построим небесную сферу, отвесную линию, плоскость горизонта. Отметим на небесной сфере светило М.

Положение светила задается двумя сферическими координатами – азимутом и высотой.

Высотой называется угловое расстояние от истинного горизонта, измеряемое вдоль вертикала. Высота измеряется в градусах от 0˚ до 90˚. Высота светил, находящихся над истинным горизонтом, положительна (h > 0), а находящихся под истинным горизонтом (и поэтому невидимых) отрицательна (h 0), а в южном полушарии – отрицательным (δ j)

2. В этот момент чему равно зенитное расстояние? (z = δ – φ).

3. Чему равна высота данного светила? (h = 90˚ – z =( 90˚ – δ) + φ)

Нарисуйте проекцию небесной сферы на плоскость небесного меридиана. Отметьте положение светила в нижней кульминации. Определите высоту светила в нижней кульминации.

Тест «Системы небесных координат».

Каждому пропуску подберите соответствующую по смыслу фразу ( см. в конце текста) так, чтобы получился связный рассказ.

1. Простейшей из систем небесных координат является горизонтальная система. В ней основной плоскостью является (. 1. ), а точкой отсчета (. 2. ). Одной из координат является (. 3. ), измеряемая дугой вертикального круга от (. 1. ) до светила и обозначаемая буквой h. (. 3. ) измеряется (. 4. ). Вместо (. 3. ) в этой системе координат часто измеряют (. 5. ) светила, которое связано с (. 3. ) соотношением (. 6. ).

А. градусах от 0° до 90°.

Б. азимут светила А.

В. плоскость истинного горизонта..

Д. высота светила над горизонтом.

Ж. зенитное расстояние.

А. точка весеннего равноденствия.

Б. градусах от 0° до 360°.

Г. плоскость эклиптики.

Д. плоскость небесного экватора.

Е. склонение светила.

Ж. прямое восхождение светила.

З. часовой мере от 0 до 24 часов

И. точка осеннего равноденствия.

4. Определите координаты следующих точек небесной сферы для широты 55°. Проверьте себя с помощью электронного планетария.

Источник