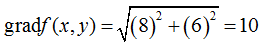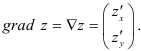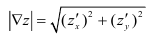Что такое градиент функции двух переменных

Градиент функции нескольких переменных

Градиентом функции называется вектор вида
для функции двух переменных формула градиента:

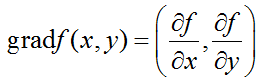
для функции трех переменных формула градиента: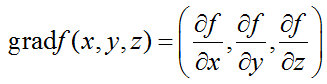

Величина градиента функции, в которой производная имеет наибольшее значение определяется по формуле:
для двух переменных:

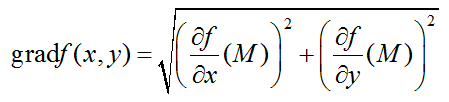
для трех переменных:

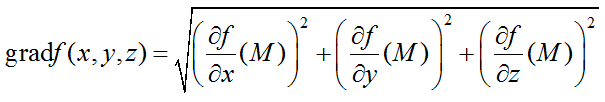
Градиент часто обозначается символом «перевернутого треугольника» — оператор Набла: ∇
Градиент дифференцируемого скалярного поля: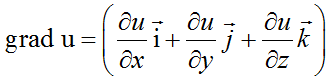

Градиент характеризует скорость изменения функции.

Пример
Найдите градиент функции двух переменных и величину градиента функции

f(x,y)=2y 3 +4x 2

в точке M(2;1).
Решение
Найдем частные производные функции первого порядка

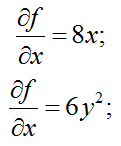
Найдем значение функции в точке M(2;1)

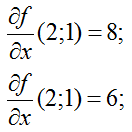
Найдем величину градиента функции в этой точке

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.6 / 5. Количество оценок: 5

Источник

Градиент функции двух переменных

Градиент функции двух переменных

Для анализа направления изменения функции двух переменных в пространстве весьма полезной является векторная характеристика — градиент. Градиентом (или вектор — градиентом) функции 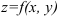называется вектор, координатами которого являются частные производные функции:

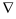
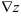
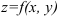
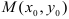
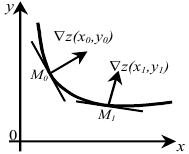
Здесь — обозначение градиента (оператор Гамильтона «набла»>. Градиент функции в данной точке характеризует направление максимальной скорости изменения функции в этой точке. Зная градиент функции в нескольких точках, можно, по крайней мере, локально, строить линии уровня функции на основе следующей теоремы: пусть задана дифференцируемая функция и пусть в точке величина градиента отлична от нуля. Тогда градиент перпендикулярен линии уровня (точнее, касательной к линии уровня), проходящей через данную точку.

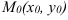
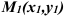
Таким образом, линии уровня можно построить следующим образом. Предположим, мы начинаем с точки . Построим в ней градиент. Задаем направление, перпендикулярное градиенту. Оно позволяет построить малую часть линии уровня. Далее рассмотрим близкую точку и построим градиент в ней. Продолжая этот процесс, можно (с определенной погрешностью) построить линии уровня.

Как и в случае обычных векторов, длину (или модуль) вектора — градиента можно определить в каждой точке по формуле

Модуль градиента — величина максимальной скорости изменения функции в данной точке по направлению, показываемому вектором — градиентом.

Остальные темы находится на этой странице и там же можно заказать любые работы по высшей математике:

Обратите внимание на эти страниц, возможно они вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Билет №7. Градиент функции двух переменных и его свойства

Градиент функции –это вектор, координаты которого являются частными производными этой функции.

U=f(x1; x2…; xn) gradU=(u’ x1 ; u’ x2…;u’ xn)

1) Градиент показывает направление максимального возрастания функции.

2) В каждой точке области определения градиент перпендикулярен линии уровня, проходящей через эту точку(то есть касательной к линии уровня)

3) Производная по направлению вектора, перпендикулярного к вектору gradu, равна нулю.

C= √x^2 +y^2

Вопрос №8
Градиент и производная по направлению.

Если в пространстве R (2) в некоторой области D задана функция двух переменных u = u(x;y), то совокупность точек области D, в которых u(x;y)=с, (с ) образуют линии, называемые линиями уровня.

Если в пространстве R (3) в некоторой области D задана функция трех переменных u = u(x;y;z), то совокупность точек области D, в которых u(x;y;z)=с, (с ) образуют поверхности, называемые поверхностями уровня.

Градиентом дифференцируемой функции u = u(x;y) (u = u(x;y;z)) называется вектор, перпендикулярный к линии (поверхности) уровня функций u = u (x;y) (u = u (x;y;z)):

Производная по направлению вектора .

Пусть в области D задана скалярная функция u = u(x;y;z) и выделена поверхность уровня u(x;y;z)=с, на которой взята точка М(х;y;z).

Спроектируем на плоскость xoy: пр_xoyΔl=М’М’₁. Нормируем вектор ( ):

, где , , , .

Запишем полное приращение

Разделим приращение Δu на .

Переходя к пределу при → 0, будем иметь значение производной по направлению вектора в R (3) : .

Производная по направлению – скорость роста функции u(x;y;z) по направлению вектора .

Связь производной по направлению и градиента.

Терема. Если в области D пространства R (3) задана непрерывная дифференцируемая функция u = u(x;y;z), определены в любой точке D

то производная по направлению вектора равна проекции градиента на его направление, то есть .

Свойства производной по направлению.

БИЛЕТ № 9.

Определение локального экстремума функции 2-х переменных:

Если в D присутствует такая окрестность UM0 точки M0, что для всех точек

А если же для всех точек

Локальный максимум и локальный минимум называются локальными экстремумами функции z(x,y).

Пример локального максимума, не являющегося максимумом на области определения.

Z= (x²+y²+1)×(cos( /2(x²+y²))

Пример точки экстремума, в которой не существует производной ни по одному направлению.

z=√x²+y² (Под корнем выражение x²+y²)

Рассмотрим точку (0;0). В этой точке направление y=kx.

Производная по x =(1/(2×√x²+(kx)²))×(2x+(k×2x)) ( Под корнем выражение x²+(kx)² )

(Корень рассматриваем арифметический). Ни по одному направлению производной не существует, хоть точка и является экстремумом.

Источник

Производная по направлению, градиент функции: объяснение, примеры

Понятие производной по направлению

Понятие производной по направлению рассматривается для функций двух и трёх переменных. Чтобы понять смысл производной по направлению, нужно сравнить производные по определению

И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой прямой, направление которой определяется вектором, произвольно заданным в задаче.

Для того, чтобы перейти к строгому математическому определению производной по направлению, нужно рассмотреть:

Величину отрезка MM 1 можно обозначить .

Функция u = f(M) при этом получит приращение

.

Определение производной по направлению. Предел отношения при , если он существует, называется производной функции u = f(M) по направлению вектора l и обозначается , то есть

.

Формула, которой нужно пользоваться для нахождения производной по направлению, следующая:

.

Смысл этой формулы: производная по направлению является линейной комбинацией частных производных, причём направляющие косинусы показывают вклад в производную по направлению соответствующей частной производной.

Примеры нахождения производной по направлению

Пример 1. Найти производную функции в точке M 0 (1; 2; 3) по направлению вектора .

Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:

Теперь можем найти производную по направлению данной функции по её формуле:

Пример 3. Найти производную функции в точке M 0 (1; 1; 1) по направлению вектора .

Решение. Найдём направляющие косинусы вектора

Найдём частные производные функции в точке M 0 :

Следовательно, можем найти производную по направлению данной функции по её формуле:

.

Градиент функции

Градиент функции нескольких переменных в точке M 0 характеризует направление максимального роста этой функции в точке M 0 и величину этого максимального роста.

Как найти градиент?

Нужно определить вектор, проекциями которого на оси координат являются значения частных производных , , этой функции в соответствующей точке:

.

То есть, должно получиться представление вектора по ортам координатных осей, в котором на каждый орт умножается соответствующая его оси частная производная.

Для градиента функции двух переменных формула короче:

.

Решение. Найдём частные производные функции в точке M 0 :

Следовательно, можем записать искомый градиент данной функции:

.

Источник

Градиент заданной функции

Вы будете перенаправлены на Автор24

Определить градиент заданной функции

Решение:

Выражение для градиента находим по формуле

Частные производные имеют вид:

\[\overrightarrow =2x\cdot \overrightarrow +4y\cdot \overrightarrow .\]

Готовые работы на аналогичную тему

Определить градиент заданной функции

Решение:

Выражение для градиента в заданной точке находим по формуле

\[\left(\overrightarrow \right)_ =\left(\frac<\partial z> <\partial x>\right)_ \cdot \overrightarrow +\left(\frac<\partial z> <\partial y>\right)_ \cdot \overrightarrow .\]

Частные производные имеют вид:

\[\left(\overrightarrow \right)_ =\overrightarrow +4\cdot \overrightarrow \]

Записать уравнение линии уровня в условиях примера 2.

Решение:

Выражение для линии уровня имеет вид:

В условиях примера 2 получаем:

Подставив координаты точки, вычислим значение константы:

Определить градиент заданной функции

Решение:

Выражение для градиента находим по формуле

Частные производные имеют вид:

\[\overrightarrow =2x\cdot \overrightarrow +4y\cdot \overrightarrow +2\cdot \overrightarrow .\]

Определить градиент заданной функции

Решение:

Выражение для градиента в заданной точке находим по формуле

\[\left(\overrightarrow \right)_ =\left(\frac<\partial w> <\partial x>\right)_ \cdot \overrightarrow +\left(\frac<\partial w> <\partial y>\right)_ \cdot \overrightarrow +\left(\frac<\partial w> <\partial z>\right)_ \cdot \overrightarrow .\]

Частные производные имеют вид:

\[\left(\overrightarrow \right)_ =2\cdot \overrightarrow +8\cdot \overrightarrow +6\cdot \overrightarrow \]

Перечислим некоторые свойства градиента:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 21 04 2021

Источник