Что такое граф в математике дискретной

Лекция 10. Графы

Начало теории графов все единодушно относят к 1736 г., когда Л. Эйлер не только решил популярную в то время задачу о кёнигсбергских мостах, но и нашел критерий существования в графе специального маршрута, который сегодня называют эйлеровым циклом. Однако эти результаты Эйлера более ста лет являлись, по сути, единственным достижением математической дисциплины, которую позднее назовут теорией графов. Лишь в середине XIX века инженер-электрик Г. Кирхгоф разработал теорию графов, называемых деревьями, для исследования электрических цепей, а математик А. Кэли в связи с описанием строения углеводородов решил перечислительные задачи для трех видов деревьев. К этому же периоду относится появление знаменитой проблемы четырех красок. Родившись при решении головоломок и занимательных игр, теория графов в настоящее время предоставляет в распоряжение инженера исключительно удобный математический аппарат для моделирования структурных свойств систем и отношений между объектами самой разнообразной природы. Благодаря наглядности и простоте этот аппарат завоевал широкое признание и повсеместно используется в инженерных исследованиях и в научно-технической литературе. В теоретической механике графы используются при вычислении скоростей многозвенных механизмов. Среди множества графов принято различать три типа: ориентированные, неориентированные и смешанные графы. Некоторые авторы выделяют еще и геометрические графы.

4.1. Основные понятия и термины

Определение графа

Довольно часто в исследованиях приходится иметь дело с множествами, содержащими элементы различной математической структуры, например, элементами такого множества могут быть точки плоскости вместе с линиями, соединяющими какие-то из этих точек. Можно еще вспомнить и «школьную» алгебру (как мы уже знаем, «по-взрослому» она называется полем действительных чисел), элементами которой являются и действительные числа, и операции сложения и умножения действительные чисел. Для идентификации единого целого (множества), объекты (элементы) которого имеют различное математическое строение, часто употребляют вместо термина «множество» термин «совокупность», пользуясь при этом везде, где это необходимо, угловыми скобками вместо привычных фигурных скобок .

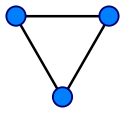
Предметом первых задач теории графов были конфигурации, состоящие из точек и линий, связывающих некоторые точки. Примеры таких конфигураций представляет рис. 4.1.

В этих задачах было совершенно безразлично, соединяют ли две концевые точки прямые линии или же эти точки соединяются криволинейными дугами. Так же не принималась во внимание и протяженность линии. Существенным и важным было только то обстоятельство, что каждая линия соединяет две конкретные точки. Таким образом, обе конфигурации (графа), изображенные на рис.4.1, идентичны. В результате рассмотрения таких задач пришли к следующему определению графа как абстрактного математического понятия.

Точки и линии, о которых речь шла выше, в определении графа предстали вершинами и ребрами. Определение ребра как пары вершин говорит только о наличии между вершинами пары определенной связи, ничего другого из этого не следует. Примерами вершин графа могут служить аэропорты, электростанции, телефонные узлы, различные технические процессы, а ребра представляют авиалинии, телефонные линии, операции и работы, задействованные в технических процессах.

Число вершин графа называется его порядком, число ребер — размером графа. Такой граф называют — графом. Вершины графа, как правило, будем обозначать символами , а его ребра символами . Для обозначения отдельных вершин будем также использовать символы , , , а для обозначения отдельных ребер — символы , .

Различные ребра графа могут соответствовать одним и тем же парам его вершин. Такие ребра называются кратными (или параллельными).

Отношение инцидентности можно задать списком ребер графа. Каждая строка этого списка соответствует определенному ребру, в ней выписаны инцидентные ему вершины. Для неориентированного графа порядок записи вершин в строке может быть произволен, для ориентированного графа первой записывается начальная вершина ребра и только потом записывается его конечная вершина.

Ребра графа, представляющие упорядоченные пары различных его вершин, обычно называют дугами (ориентированным ребрами), а ребра, за которыми стоят неупорядоченные пары различных вершин, будем называть звеньями (неориентированными ребрами). Ребра графа, отвечающие парам одинаковых вершин, называют петлями, и в этом случае . Дуги, которым соответствуют пары и , принято называть противоположно направленными. Иногда две противоположно направленные дуги заменяют одной биориентированной дугой, т.е. дугой, имеющей два направления.

Граф, среди ребер которого есть и дуги и звенья, называют смешанным графом.

Граф, ребра которого являются либо дугами, либо петлями, называют ориентированным графом (или орграфом).

Заменяя все дуги орграфа дугами противоположно им направленными, получим орграф, обратный исходному орграфу.

Граф, ребрами которого могут быть только звенья либо петли, называют неориентированным графом (или неографом). В ситуациях, когда имеют дело только с неориентированными графами или когда исключены возможные недоразумения, допустимо звенья неориентированного графа называть просто «ребрами».

В прикладных задачах намного чаще приходится иметь дело только с простыми ориентированными или с простыми неориентированными графами, и в тех случаях, когда это не приводит к недоразумениям, принято, опуская слово «простые», коротко называть такие графы соответственно орграфами и графами (крайне редко – неографами).

Выписанные выше соображения позволяют утверждать о равносильности обоих определений в случае орграфа без кратных дуг.

Две противоположно направленные дуги, говорящие о наличии связи между вершинами графа в обоих направлениях, в некоторых практических задачах равноценны неориентированной связи между этими вершинами и могут быть заменены в этих задачах одним звеном. После такой замены в орграфе мы придем к смешанному графу. При решении ряда задач неориентированный или смешанный граф бывает полезно преобразовывать в орграф, подменяя каждое звено такого графа парой противоположно направленных дуг.

Заменяя две противоположно направленные дуги одним звеном и снимая ориентацию со всех остальных дуг орграфа, получим неориентированный граф, который называют неориентированным дубликатом (иначе — основанием) исходного орграфа.

При решении конкретных задач могут быть использованы графы различного вида. Все определяется спецификой самой задачи. Рассмотрим, например, задачу организации автомобильного движения в некотором городе. Схему организации движения автотранспорта представит ориентированный мультиграф, если вершинами графа считать перекрестки дорог, а его ребрам сопоставить полосы движения по дорогам, соединяющим перекрестки. Если при составлении схемы принимать во внимание возможность разворота на отдельных перекрестках, отображая такую возможность с помощью петли, то в этом случае схему организации движения будет представлять псевдограф. Полагая, что ребрам графа соответствуют дороги, связывающие перекрестки, различая при этом дороги с односторонним движением (дуги) и с двусторонним движением (звенья), придем к смешанному графу. Кстати, за вершины графа можно принять улицы города, интерпретируя перекрестки как ребра графа. Две вершины (улицы) связаны дугой, если имеется перекресток, по которому можно из первой улицы (вершины) непосредственно переехать на вторую улицу (вершину). Построенный таким образом простой орграф может быть полезен, например, при составлении оптимальных маршрутов проезда по городу.

Источник

Граф (математика)

В математической теории графов и информатике граф — это совокупность непустого множества вершин и множества пар вершин (связей между вершинами).

Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.

Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные рёбра) — гиперссылки (см. Тематическая карта).

Содержание

Определения

Теория графов не обладает устоявшейся терминологией. В различных статьях под одними и теми же терминами понимаются разные вещи. Ниже приведены наиболее часто встречаемые определения.

Граф, или неориентированный граф — это упорядоченная пара , для которой выполнены следующие условия:

(а значит и, , иначе оно было бы мультимножеством) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становится ложным в случае бесконечных множеств.

Вершины и рёбра графа называются также элементами графа, число вершин в графе — порядком, число рёбер — размером графа.

Вершины и называются концевыми вершинами (или просто концами) ребра . Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.

Два ребра называются смежными, если они имеют общую концевую вершину.

Два ребра называются кратными, если множества их концевых вершин совпадают.

Ребро называется петлёй, если его концы совпадают, то есть .

Степенью вершины называют количество инцидентных ей рёбер (при этом петли считают дважды).

Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.

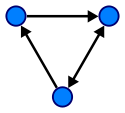
Ориентированный граф

Ориентированный граф (сокращённо орграф) — это упорядоченная пара , для которой выполнены следующие условия:

Дуга — это упорядоченная пара вершин , где вершину называют началом, а — концом дуги. Можно сказать, что дуга ведёт от вершины к вершине .

Смешанный граф

Смешанный граф — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой , где , и определены так же, как выше.

Ориентированный и неориентированный графы являются частными случаями смешанного.

Изоморфные графы

Граф называется изоморфным графу , если существует биекция из множества вершин графа в множество вершин графа , обладающая следующим свойством: если в графе есть ребро из вершины в вершину , то в графе должно быть ребро из вершины в вершину и наоборот — если в графе есть ребро из вершины в вершину , то в графе должно быть ребро из вершины в вершину . В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.

Прочие связанные определения

Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.

Ориентированным путём в орграфе называют конечную последовательность вершин , для которой все пары являются (ориентированными) рёбрами.

Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины и являются концами некоторого ребра, то согласно данному определению, последовательность является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.

Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:

Бинарное отношение на множестве вершин графа, заданное как «существует путь из в », является отношением эквивалентности и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.

Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа . Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов

Ребро графа называется мостом, если его удаление увеличивает число компонент.

Дополнительные характеристики графов

Обобщение понятия графа

Простой граф является одномерным симплициальным комплексом.

Более абстрактно, граф можно задать как тройку , где и — некоторые множества (вершин и рёбер, соотв.), а — функция инцидентности (или инцидентор), сопоставляющая каждому ребру (упорядоченную или неупорядоченную) пару вершин и из (его концов). Частными случаями этого понятия являются:

Под данное выше определение не подходят некоторые другие обобщения:

Способы представления графа в информатике

Матрица смежности

Таблица, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).

Недостатком являются требования к памяти, прямо пропорциональные квадрату количества вершин.

Матрица инцидентности

Каждая строка соответствует определённой вершине графа, а столбцы соответствуют связям графа. В ячейку на пересечении -ой строки с -м столбцом матрицы записывается:

1 в случае, если связь «выходит» из вершины , −1, если связь «входит» в вершину, 0 во всех остальных случаях (то есть если связь является петлёй или связь не инцидентна вершине)

Данный способ является самым ёмким (размер пропорционален ) для хранения, но облегчает нахождение циклов в графе.

Список рёбер

Список рёбер — это тип представления графа, подразумевающий, что каждое ребро представляется двумя числами — номерами вершин этого ребра.

Языки описания и программы построения графов

Для описания графов в целях, пригодных для машинной обработки и одновременно удобном для человеческого восприятия используется несколько стандартизированных языков, среди которых:

Отметим специализированные коммерческие программы для построения графов:

Из бесплатных можно отметить:

Для визуализации графов можно использовать:

См. также

Литература

Полезное

Смотреть что такое «Граф (математика)» в других словарях:

Граф — Граф: От древневерхненемецкого gravo, gravio «предводитель, вождь»: Граф (титул) дворянский титул; «Граф» короткометражная немая кинокомедия Чарли Чаплина (The Count, 1916). От греч. γράφω «царапаю, черчу, пишу»: Граф… … Википедия

Граф зависимостей — В математике, информатике и цифровой электронике, граф зависимостей представляет собой ориентированный граф, отражающий зависимости нескольких объектов друг к другу. По графу зависимостей можно определить порядок вычислений или его недостатки,… … Википедия

Граф объектный — это совокупность узлов и ребер, соединяющих эти узлы. Объектные графы обеспечивают простой способ учета взаимных связей в множестве объектов, и не обязательно, чтобы эти связи в точности проецировались в классические связки объектно… … Википедия

Граф Келли (теория групп) — Граф Кэли граф, который строится по группе с выделенной системой образующих. Назван в честь английского математика Артура Кэли (A. Cayley). Определение Пусть дана дискретная группа G и система образующих S. Предположим S = S − 1, то есть, для… … Википедия

Граф Петерсена — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей … Википедия

ГРАФ СЛУЧАЙНЫЙ — вероятностная модель, предназначенная для изучения частотных характеристик различных параметров графов. Под Г. с. обычно понимается нек рый класс графов на к ром задано распределение вероятностей. Произвольный конкретный граф Gиз наз. реализацией … Математическая энциклопедия

Граф — Антон (Graf, Anton) 1736, Винтертур 1813, Дрезден. Немецкий живописец. Учился в 1753 1756 у И. У. Шелленберга в Винтертуре, затем у И. Я. Хайда в Аугсбурге. Работал как портретист в Регенсбурге, Винтертуре, Аугсбурге, Мюнхене, Цюрихе. С 1766… … Европейское искусство: Живопись. Скульптура. Графика: Энциклопедия

Объектный граф — Граф объектный это совокупность узлов и ребер, соединяющих эти узлы. Объектные графы обеспечивают простой способ учёта взаимных связей в множестве объектов, и не обязательно, чтобы эти связи в точности проецировались в классические связки… … Википедия

Гамильтонов граф — Граф додекаэдра с выделенным циклом Гамильтона … Википедия

Планарный граф — Планарный граф граф, который может быть изображен на плоскости без пересечения ребер. Более строго: Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим … Википедия

Источник