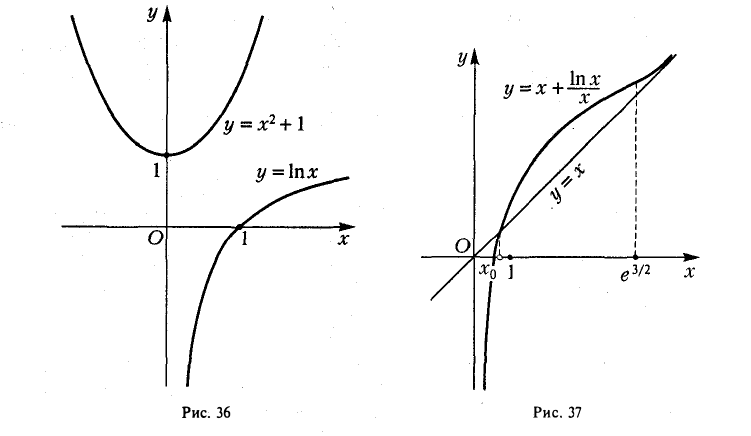
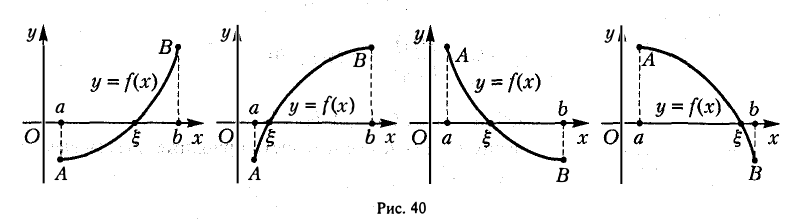
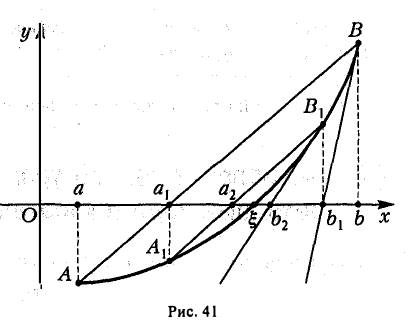
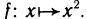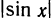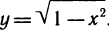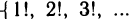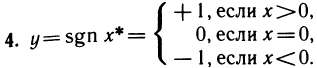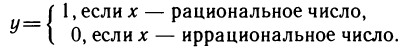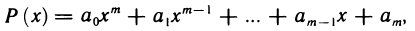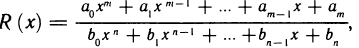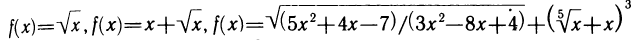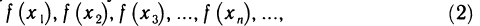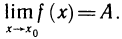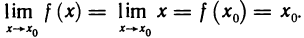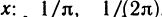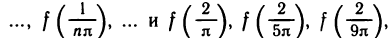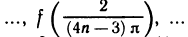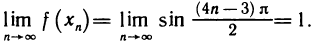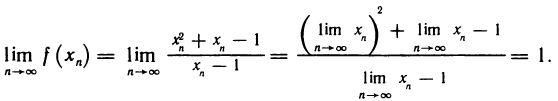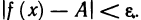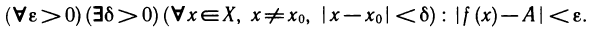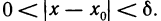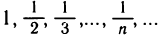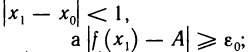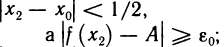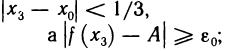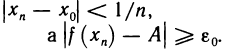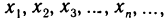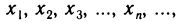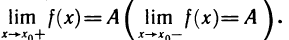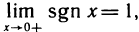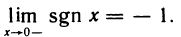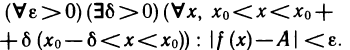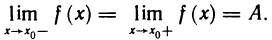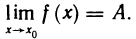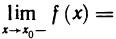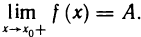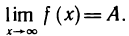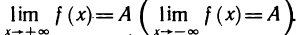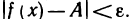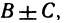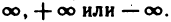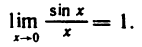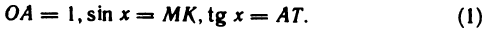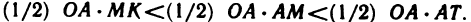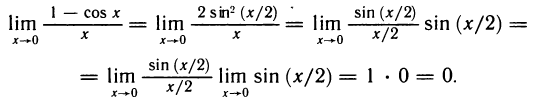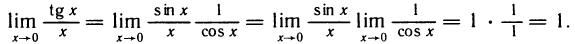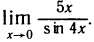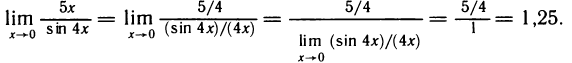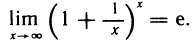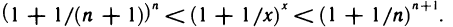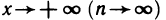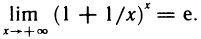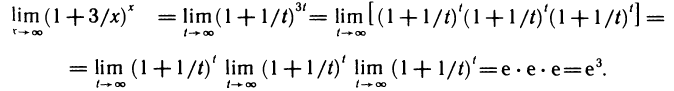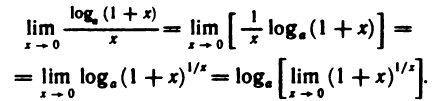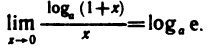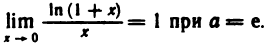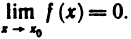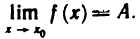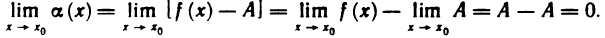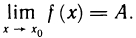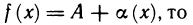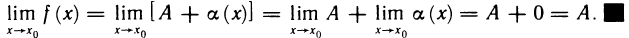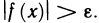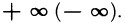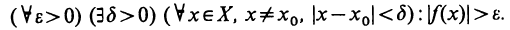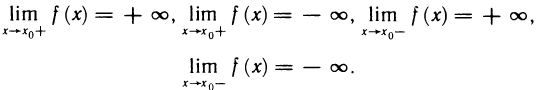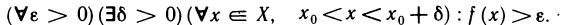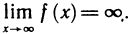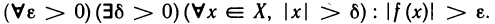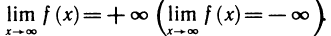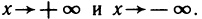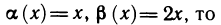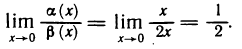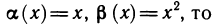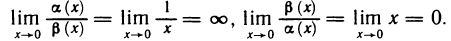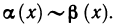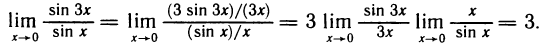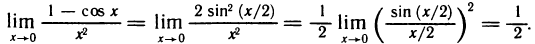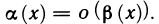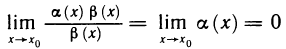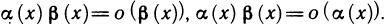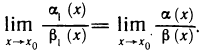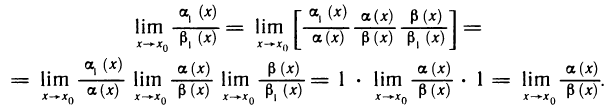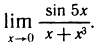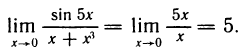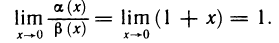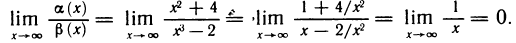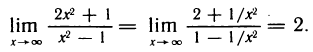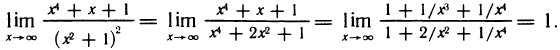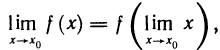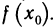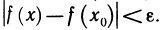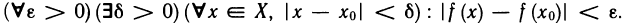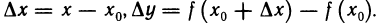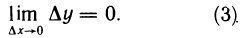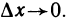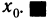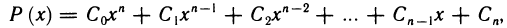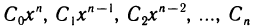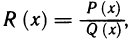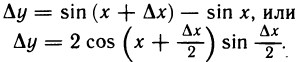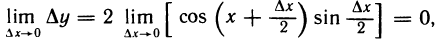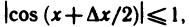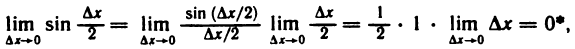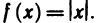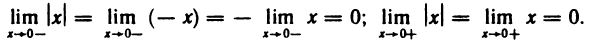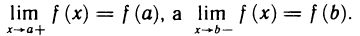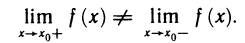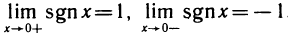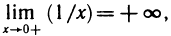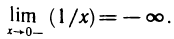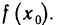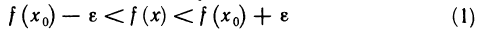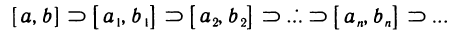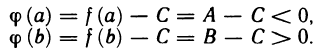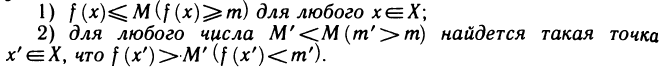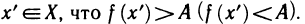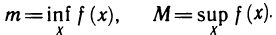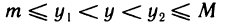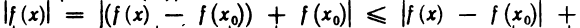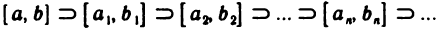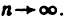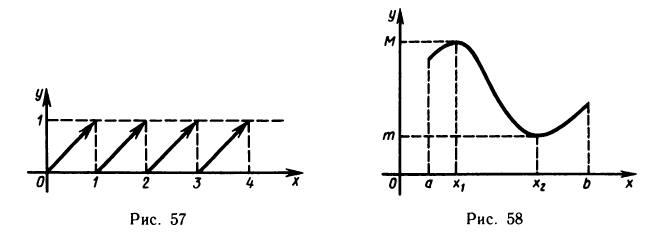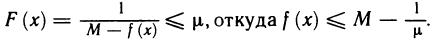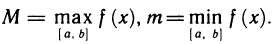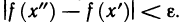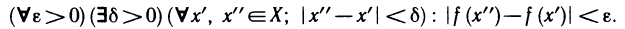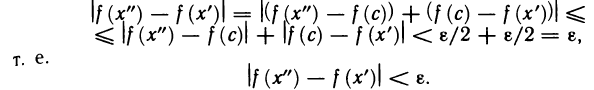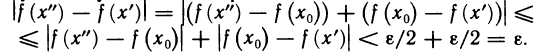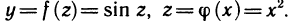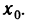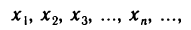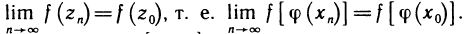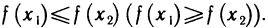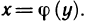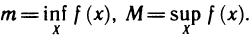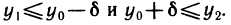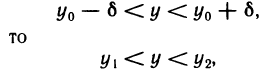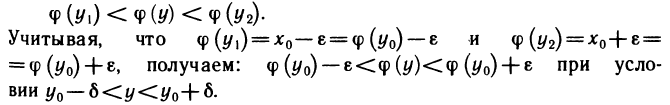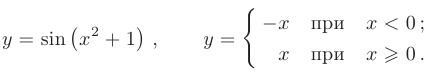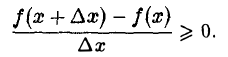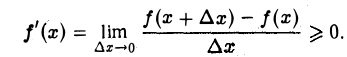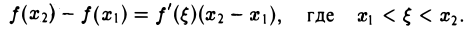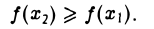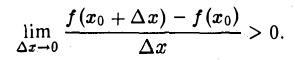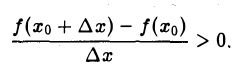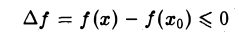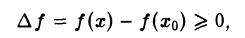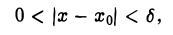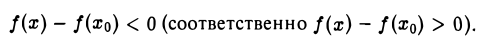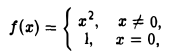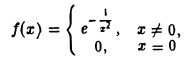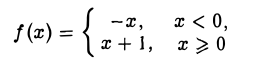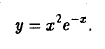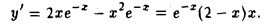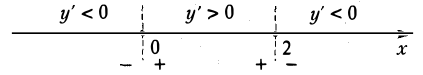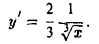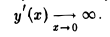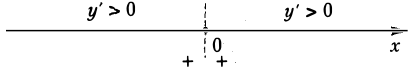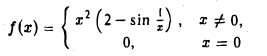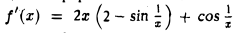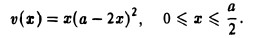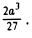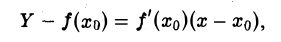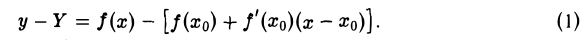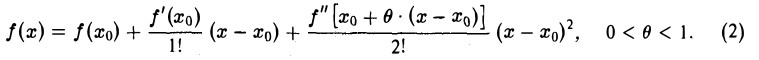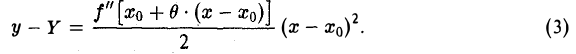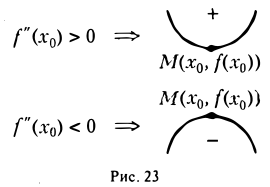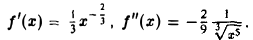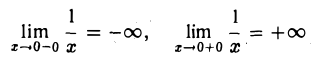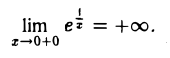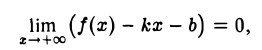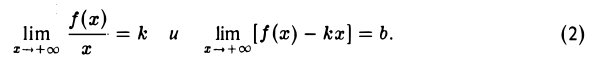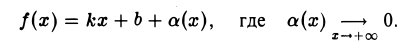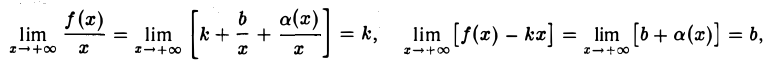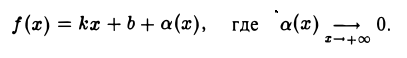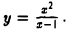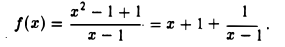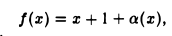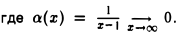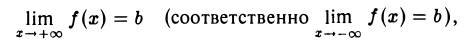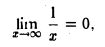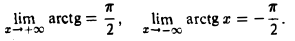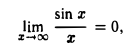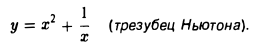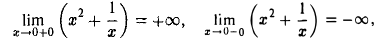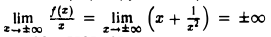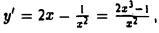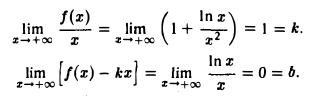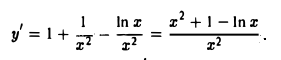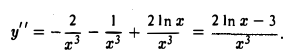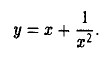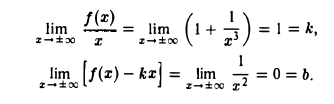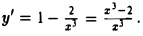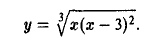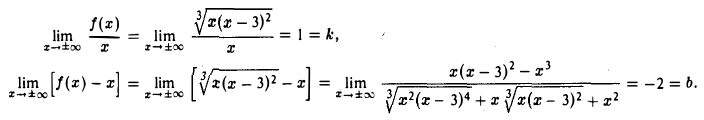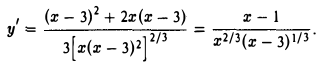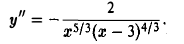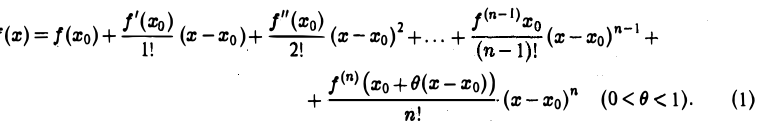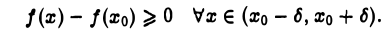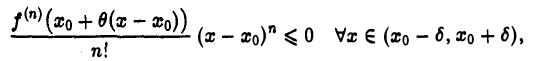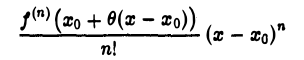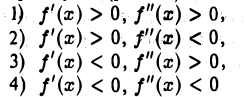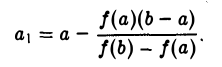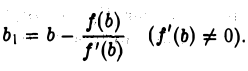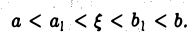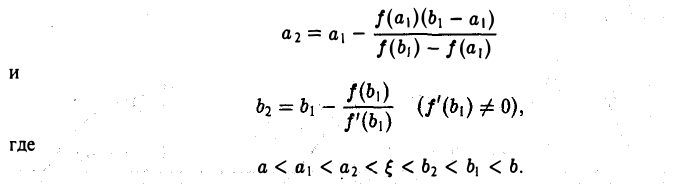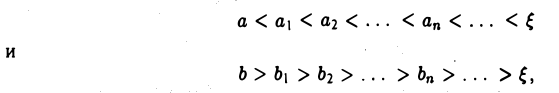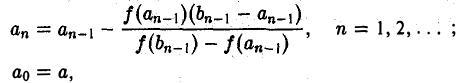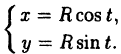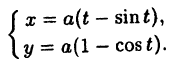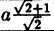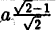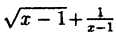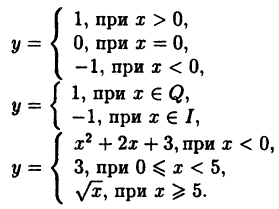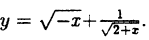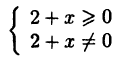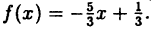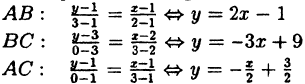Что такое график функции одной переменной
Что такое функция?
7 класс, 11 класс, ЕГЭ/ОГЭ
Понятие функции
Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.
1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.
Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.
Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.
2. Функция — это определенное действие над переменной.
Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.
В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:
В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.
3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.
Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида
область определения выглядит так:
И записать это можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.
В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.
Тема 1. ФУНКЦИЯ ОДНОЙ ПЕРЕМЕННОЙ
1.1. Определение функции одной переменной
Определение. Пусть даны два множества X и Y. Если каждому элементу x из множества X по некоторому правилу f соответствует единственный элемент y из множества Y, то говорят, что на множестве X определена функция y = f ( x ) с областью определения X = D( f ) и областью изменения Y = E ( f ). При этом x считают независимой переменной, или аргументом функции, а y – зависимой переменной или функцией.
Частным значением функции y = f ( x ) при фиксированном значении аргумента x = x0 называют y 0 = f ( x 0 ).
1.2. Способы задания функции
1) Аналитический способ – способ задания функции с помощью формулы.
Различают несколько способов аналитического задания функции:
а) Функция задана явно формулой y = f ( x ).
б) Функция задана неявно уравнением, связывающем x и y : F( x ; y ) = 0.
Например: можно задать окружность 
3) Графический способ задания функции, когда зависимость функции от её аргумента задаётся графически.
1.3. Сложная и обратная функции
1.4. Элементарные функции
Основные элементарные функции:
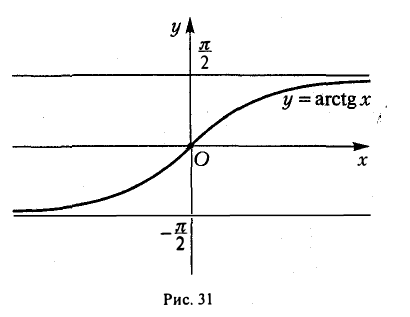
Обратные тригонометрические функции :
Элементарной функцией называется функция, составленная из основных элементарных функций с помощью конечного числа операций сложения, вычитания, умножения, деления и суперпозиции.
Например: 
Графики обратных тригонометрических функций:
Построение графиков функций
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
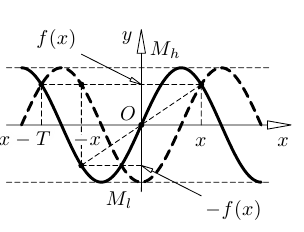
Нули функции — это значения аргумента, при которых функция равна нулю.
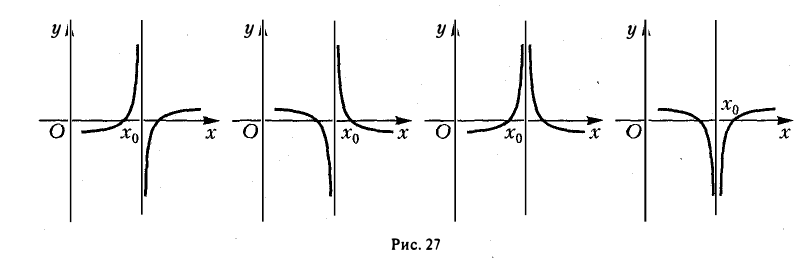
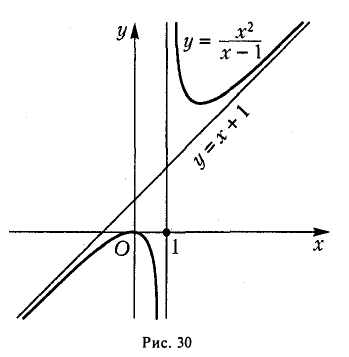
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
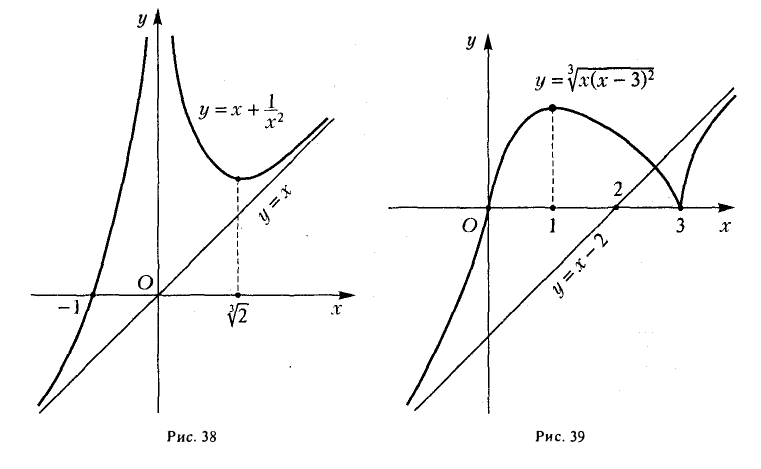
Задача 1. Построим график функции
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
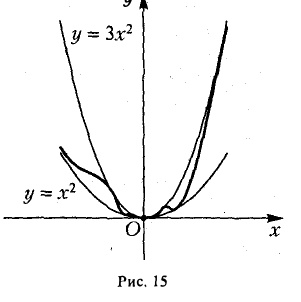
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины 
Ветви вниз, следовательно, a 0.
Координата вершины 
| x | y |
| 0 | -1 |
| 1 | 2 |
| x | y |
| 0 | 2 |
| 1 | 1 |
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
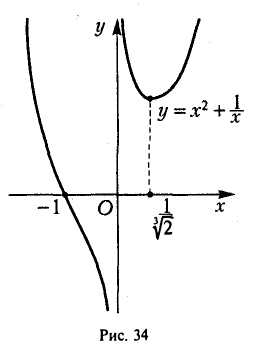
Задача 5. Построить график функции
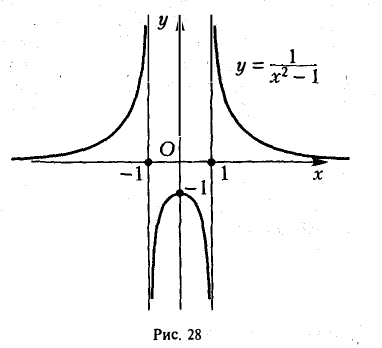
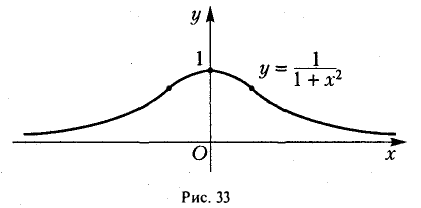
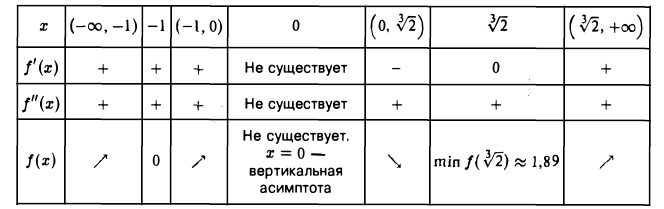
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Сдвигаем график вправо на 1:
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:
График линейной функции, его свойства и формулы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!
Свойства линейной функции
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Точки пересечения графика функции y = kx + b с осями координат:
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Функции одной переменной в математике с примерами решения и образцами выполнения
Начинаем изучение важнейшего понятия математического анализа — понятия функции. В этой главе будет введено понятие предела функции, а также понятие непрерывности функции.
Понятие функции
Определение функции. Определение. Пусть X и Y — некоторые числовые множества. Функцией называется множество f упорядоченных пар чисел (х; у) таких, что 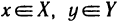
Кроме буквы f для обозначения функций используют и другие буквы, например: у=у(х), y=g(x), у =ф(х), у=А(х), у=F(х) и т. д. Другими буквами могут обозначаться зависимая и независимая переменные. Иногда зависимую переменную также называют функцией.
При вычислениях запись y = f(х) обычно удобнее записи вида f:
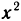
Функция, все значения которой равны между собой, называется постоянной. Постоянную функцию часто обозначают буквой С.
Про функцию f (х), определенную на некотором множестве х говорят, что она ограничена сверху (снизу) на этом множестве если существует число М (m) такое, что для любого 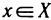
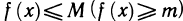
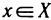
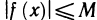
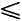
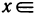
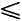
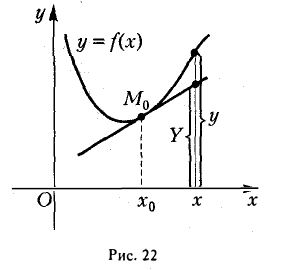
На плоскости функция изображается в виде графика — множества точек (х; у), координаты которых связаны соотношением y=f(x), называемым уравнением графика.
График функции может представлять собой некоторую «сплошную» линию (кривую или прямую), а может состоять из отдельных точек, например график функции 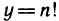
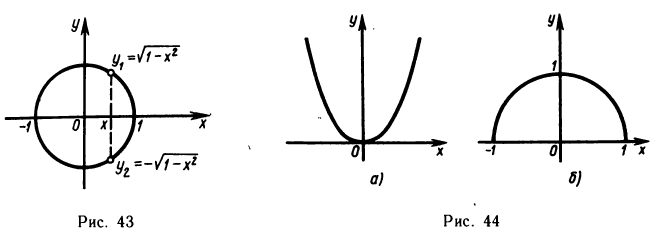
Заметим, что не всякая линия является графиком какой-либо функции. Например, окружность 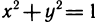
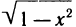
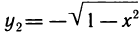
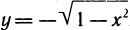
2.Способы задания функций. Задать функцию f — значит указать, как по каждому значению аргумента х находить соответствующее ему значение функции f (х). Существуют три основных способа задания функций: аналитический, табличный и графический.
1) Аналитический способ. Этот способ состоит в том, что зависимость между переменными величинами определяется с помощью формулы, указывающей, какие действия нужно выполнить, чтобы получить значение функции, соответствующее данному значению аргумента.
1.Формула 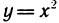
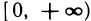
Формула 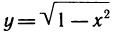
3. Формула 

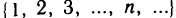
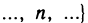
Данная функция задана с помощью нескольких формул. Она определена на всей числовой прямой 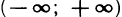
Эта функция определена на всей числовой прямой 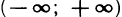
Заметим, что функцию Дирихле изобразить графически не представляется возможным.
2)Табличный способ. Приведем следующую таблицу:
Поставим в соответствие каждому х, записанному в первой троке таблицы, число у, стоящее во второй строке под этим числом х’ и будем говорить, что полученная функция задана таблицей и областью определения данной функции является множество, стоящее из девяти чисел х, перечисленных в первой строке таблицы, а множеством ее значений — множество, состоящее из девяти чисел у, перечисленных во второй ее строке.
С помощью таблицы можно задать функцию только при конец, ном числе значений аргумента. Таблицы часто используют для задания функций. Так, хорошо известны, например, таблицы тригонометрических функций, таблицы логарифмов и многие другие Примером табличного способа задания функции может служить расписание движения поезда, которое определяет местоположение поезда в отдельные моменты времени.
3) Графический способ. Графический способ задания функции обычно используют в практике физических измерений, когда соответствие между переменными х и у задается посредством графика. Во многих случаях такие графики чертятся с помощью самопишущих приборов.
Так, например, для измерения давления атмосферы на различных высотах используют специальный самопишущий прибор — барограф, который записывает на движущейся ленте в виде кривой линии изменение давления в зависимости от высоты.
3.Классификация функций. Постоянная функция f(x)=C, G=const, степенная функция 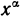

Все функции, получаемые с помощью конечного числа арифметических действий над простейшими элементарными функциями, а также суперпозицией (или наложением) этих функций, составляют класс элементарных функций. Примерами элементарных функций являются:
Имеет место следующая классификация элементарных функции-
где m
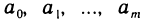
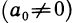
2) Функция, представляющая собой отношение двух целых рациональных функций
называется дробно-рациональной функцией.
Совокупность целых рациональных и дробно-рациональных функций образует класс рациональных функций.
3)Функция, полученная с помощью конечного числа суперпозиций и четырех арифметических действий над степенными функциями как с целыми, так и с дробными показателями и не являющаяся рациональной, называется иррациональной функцией.
и т. д. — иррациональные функции.
4)Всякая функция, не являющаяся рациональной или иррациональной, называется трансцендентной функцией. Это, например, функции f(х) = sin х, f(x) = sin х+х и т. д.
Предел функции
сходящуюся к 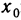
и можно ставить вопрос о существовании ее предела.
Определение 1. Число А называется пределом функции f (х) в точке х= 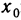

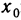
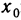
Символически это записывается так:
Функция f (х) может иметь в точке 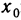
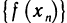
Рассмотрим примеры:
2. Функция f(х)=х имеет в любой точке 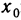
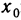
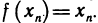

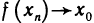
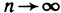
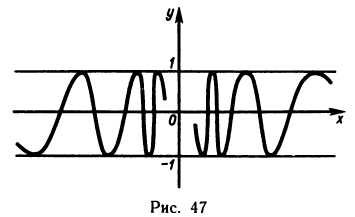
3. Функция f(x) = sin (1/х) (рис. 47), определенная для всех х
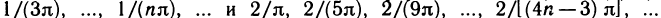
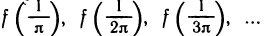
Так как при любом 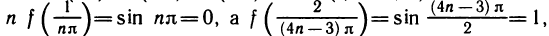
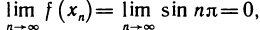
Таким образом, для двух сходящихся к нулю последовательностей значений аргумента х соответствующие последовательности значений функции имеют разные пределы. А это по определению предела функции и означает, что 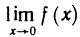
4. Функция 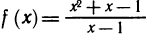
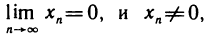
Таким образом, существует 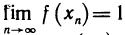
5. Функция Дирихле, значения которой в рациональных точках равны единице, а в иррациональных — нулю, не имеет предела ни в одной точке 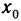
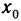
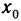
Существует другое определение предела функции
Определение:
Число А называется пределом функции f (х) в точке 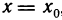
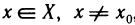
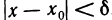
Используя логические символы, определение 2 можно записать в виде
Отметим, что неравенства 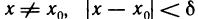
Первое определение основано на понятии предела числовой последовательности, поэтому его часто называют определением «на языке последовательностей». Второе определение называют определением «на языке е — б».
Теорема:
Первое и второе определения предела функции эквивалентны.
Доказательство:
1) Пусть А — предел f (х) в точке х0 согласно первому определению. Покажем, что А — предел согласно второму определению. Предположим обратное, т. е. А не является пределом этой функции согласно второму определению. Это значит, что не для любого е>0 можно указать такое б>0, чтобы из неравенства 
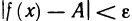
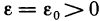
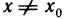
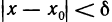
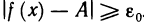
для б=1 в X существует такое 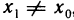
для б=1/2 в X существует такое 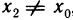
для б=1 /3 в X существует такое 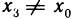
для б=1/n в X существует такое 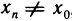
В результате получается последовательность точек, отличных от 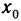
сходящаяся к точке х0, так как 

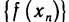
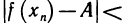
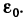
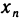
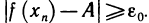
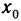
2) Пусть теперь А — предел f(х) в точке 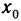
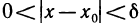
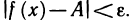
сходящуюся к точке 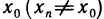
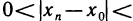

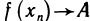
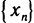
Итак, установлена эквивалентность обоих определений предела функции и можно использовать любое из них в зависимости от того, какое более удобно при решении той или иной задачи.
Заметим, что определение предела функции «на языке последовательностей» называют также определением предела функции по Гейне, а определение предела функции «на языке е-б» — определением предела функции по Коши.
2. Предел функции при 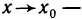
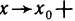
В дальнейшем будут использованы понятия односторонних пределов функции, которые определяются следующим образом.
Определение:
Число А называется правым (левым) пределом функции f(х) в точке 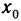
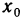
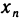
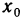
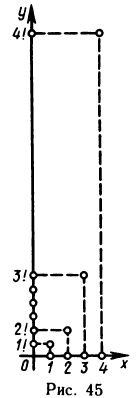
B качестве примера рассмотрим функцию f(x)= sgn х. Она имеет в точке х=0 правый и левый пределы: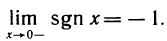
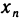
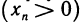
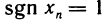
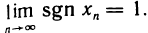
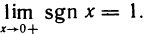
Можно дать равносильное определение односторонних пределов функции «на языке е-б»: число А называется правым (левым) пределом функции f (х) в точке 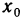
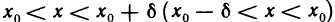
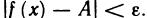
Связь между односторонними пределами и пределом функции устанавливает следующая теорема.
Теорема:
Функция f(х) имеет в точке 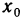
Доказательство:
Пусть
Тогда, согласно определению предела функции слева и справа, для любого е>0 существуют числа 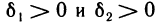


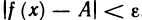
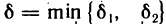
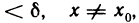
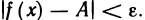
Обратно, пусть 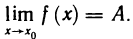
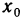
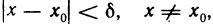
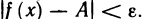


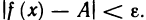
3. Предел функции при 
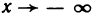
Кроме рассмотренных понятий предела функции при 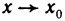
Определение:
Число А называется пределом функции f (х) при 
Символическая запись:
Определение:
Число А называется пределом функции f(х) при 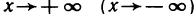
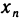
Символическая запись:
Рассмотрим пример. Пусть 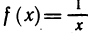

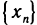
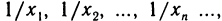
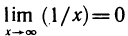
Определения 4—5 даны «на языке последовательностей». Можно дать равносильные определения «на языке е-б» и записать их с помощью логических символов. Рекомендуем сделать это самостоятельно. В качестве примера сформулируем определение предела функции при
Определение:
Число А называется пределом функции f (х) при 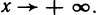
Теоремы о пределах функций
Определение предела функции «на языке последовательностей» дает возможность перенести доказанные выше теоремы о пределах последовательностей на функции. Покажем это на примере двух теорем.
Теорема:
Пусть функции f(х) и g(х) имеют в точке 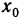
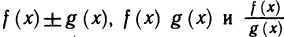
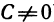
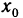
Доказательство:
Пусть 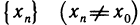
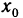
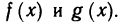
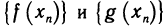
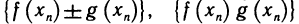
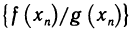
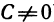
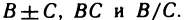
Теорема:
Пусть функции 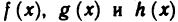
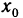
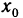
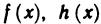
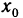
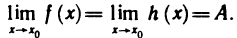
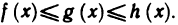
Доказательство:
Пусть 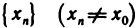
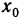
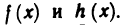
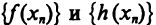
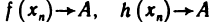
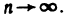
Отсюда по теореме 2.11 следует, что 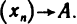
Замечание:
Теоремы 4.3 и 4.4 верны также и в случае, когда 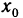
Два замечательных предела
Первый замечательный предел
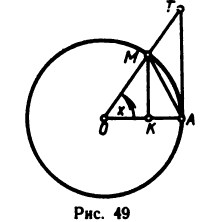
Докажем, что
Рассмотрим дугу окружности радиуса R=1 с центральным углом, радианная мера которого равна 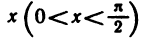
Очевидно, что площадь треугольника ОАМ меньше площади сектора ОАМ, которая меньше площади треугольника ОАТ, или, что то же самое,
Принимая во внимание равенства (1), последнее соотношение можно записать в виде 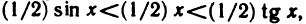
Разделив эти неравенства на sin х, получим 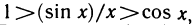
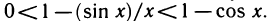
Пример:
Найти
Решение:
Имеем
Пример:
Найти
Решение:
Имеем
Второй замечательный предел
Докажем, что
Как известно, 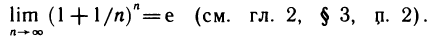
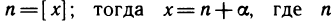
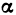
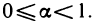
При
Отсюда по теореме 4.4 получаем
Пусть теперь x
Пример:
Найти 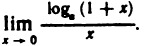
Решение:
Для нахождения предела преобразуем данную дробь:
Но 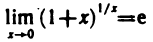
В частности,
Бесконечно малые функции
Определение:
Функция f (х) называется бесконечно малой функцией (или просто бесконечно малой) в точке 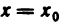

Аналогично определяются бесконечно малые функции при
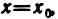
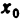
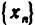
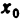
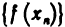
Теорема:
Для выполнения равенства 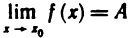
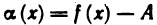
Доказательство:
Необходимость. Пусть
Рассмотрим разность 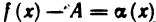
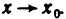
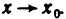
Достаточность. Пусть 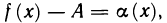
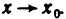
Так как
Из теоремы 4.5 получаем специальное представление для функции, имеющей в точке 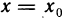
При этом обычно говорят, что функция f (х) в окрестности точки 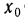
Бесконечно малые функции обладают такими же свойствами, что и бесконечно малые последовательности. Справедлива следующая теорема.
Теорема:
Алгебраическая сумма и произведение конечного числа бесконечно малых функций при 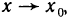
Эта теорема непосредственно вытекает из первого определения предела функции и теорем 2.2—2.4.
Все сказанное о бесконечно малых функциях при 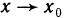
Бесконечно большие функции
Определение:
Функция f(х) называется бесконечно большой функцией (или просто бесконечно большой) в точке 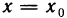
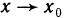
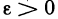
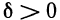
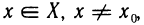
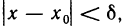
В этом случае пишут 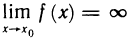
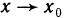
Если же выполняется неравенство 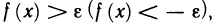
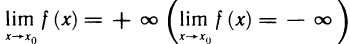
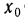
Используя логические символы, определение 2 можно записать в виде
По аналогии с конечными односторонними пределами определяются и бесконечные односторонние пределы:
Так, например, пишут 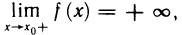
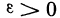
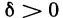
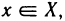
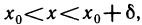
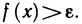
«На языке последовательностей» это же определение записывается так: 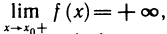
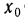
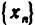
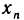
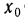
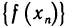
Точное определение других подобных пределов рекомендуем сделать самостоятельно.
Аналогично определяются бесконечно большие функции при 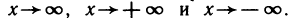
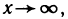

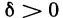
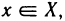
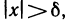
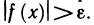
Символическая запись определения бесконечно большой функции при
Если же выполняется неравенство 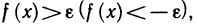
Предлагаем самостоятельно сформулировать определение бесконечно большой функции при
В заключение покажем, что между бесконечно малыми и бесконечно большими функциями существует такая же связь, как и между соответствующими последовательностями, т. е. функция, обратная бесконечно малой, является бесконечно большой, и наоборот.
В самом деле, пусть 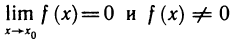
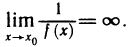

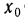
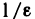
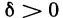
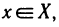
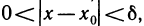
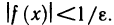
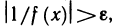
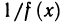
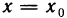
Сравнение бесконечно малых и бесконечно больших функций
Как было показано, сумма, разность и произведение бесконечно малых функций являются бесконечно малыми функциями. Этого, вообще говоря, нельзя сказать о частном: деление одной бесконечно малой на другую может привести к различным результатам. Так, например, если
Если же
Рассмотрим правила сравнения бесконечно малых функций. Пусть при 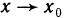
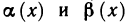
1) если 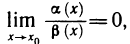
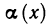
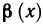
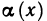
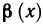
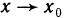
2) если 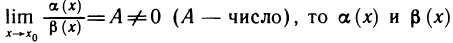
3) если 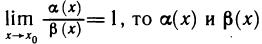
В некоторых случаях недостаточно знать, что одна из двух бесконечно малых является бесконечно малой более высокого порядка, чем другая. Нужно еще оценить, как высок этот порядок. Поэтому вводится следующее правило:
4) если 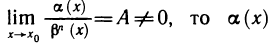
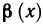
Существуют аналогичные правила для сравнения бесконечно малых функций при 
Рассмотрим примеры:
1. Функции 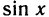

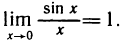
2. Функции 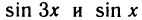

3. Функция 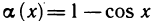

При сравнении бесконечно малых функций часто используют символ о («о малое»). Если функция 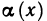
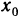
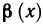
Если функции 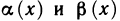
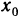
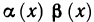
и поэтому
Если 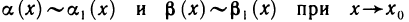
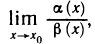
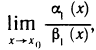
В самом деле, имеем
Доказанное утверждение во многих случаях упрощает вычисление пределов
Пример:
Найти
Решение:
Так как 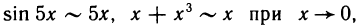
Для бесконечно больших функций имеют место аналогичные правила сравнения.
Рассмотрим несколько примеров.
1. Функции 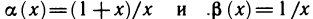

В этом случае говорят также, что 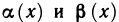
2. Функция 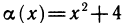
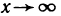
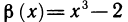
3. Бесконечно большие при 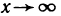
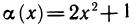
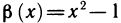
4. Функция 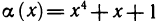
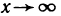
Понятие непрерывности функции
Понятие непрерывности функции является одним из основных понятий математического анализа.
Определение непрерывности функции
Пусть функция 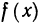
Определение:
Функция 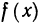
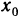
Так как 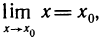
т. е. для непрерывной функции можно переставить знак функции и знак предела.
Приведем равносильное определение непрерывности функции «на языке последовательностей»: функция 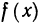
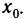
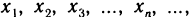
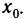
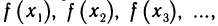
Сформулируем определение непрерывности функции «на языке 
Определение:
Функция 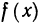
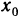

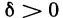
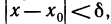
Эквивалентность этих определений очевидна.
Запишем определение 2, используя логические символы:
Если 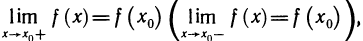
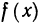
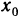
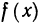
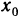
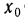
Приведем еще одно определение непрерывности функции, которое по существу является перефразировкой первого определения. Перенесем в равенстве (1) 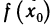
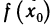
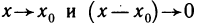
Разность 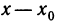
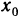
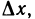
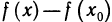
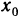
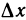
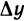
Отметим, что при фиксированной точке 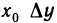
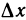
Соотношение (3) и является еще одним определением непрерывности функции, которое можно сформулировать так.
Определение:
Функция 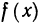
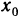
Последнее определение для практического использования бывает иногда более удобным, и им будем также пользоваться.
Арифметические действия над непрерывными функциями
Теорема:
Пусть функции 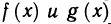
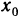
Тогда функции 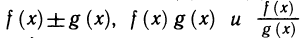
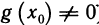
Доказательство:
Так как непрерывные в точке 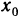
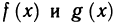
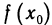
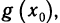
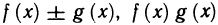
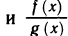
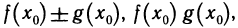
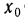
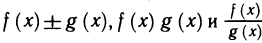
Непрерывность некоторых элементарных функций
Одним из важных свойств элементарных функций является их непрерывность в каждой точке, в окрестности которой они определены. На примере некоторых функций проверим данный факт, используя определение непрерывности функции в точке и теорему 4.7.
Непрерывность рациональных функций
Простейшим примером функции, непрерывной в любой точке 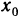
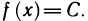
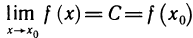
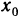
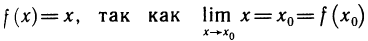
предел функции в точке 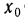
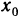
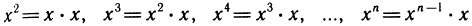
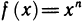
где 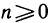
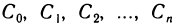
есть произведение двух непрерывных функций (постоянной и степенной). По теореме 4.7 оно непрерывно в любой точке х. Многочлен Р (х) является, таким образом, суммой функций, непрерывных в любой точке х, и, следовательно, непрерывен в любой точке х.
Дробно-рациональная функция, т. е. функция вида
где 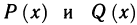
Например, функция 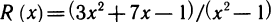
Непрерывность тригонометрических функций
Рассмотрим тригонометрические функции 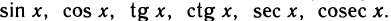
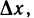
Переходя к пределу в левой и правой частях равенства при 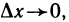
так как
а произведение ограниченной функции на бесконечно малую есть бесконечно малая. Таким образом, функция sin х непрерывна в любой точке х.
Непрерывность функции cos х в любой точке х доказывается аналогично.
Из непрерывности функций 
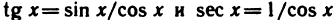
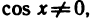
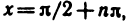
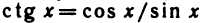
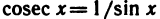
Непрерывность функции
Функция 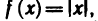
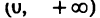
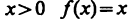
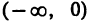
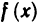
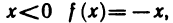
Итак, пределы функции в точке х=0 слева и справа совпадают и равны значению функции в этой точке. Отсюда следует, что функция |х| непрерывна в точке х=0 и, следовательно, непрерывна во всех точках числовой прямой.
Таким образом, рассмотренные функции непрерывны в каждой точке, в окрестности которой они определены. На основании теоремы 4.7 о непрерывности суммы, разности, произведения и частного можно утверждать, что функции, получаемые из них с помощью конечного числа арифметических действий, являются также непрерывными функциями в каждой точке, в окрестности которой они определены.
Будем говорить, что функция f(х) непрерывна в интервале (а, b), если она непрерывна в каждой точке этого интервала; непрерывна на отрезке 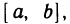
Классификация точек разрыва функции
Определение и классификация точек разрыва функции:
Определение:
Точка 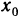
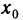
Разрывы функций классифицируются следующим образом.
Разрыв 1-го рода. Точка 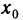
Пример:
Для функции 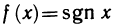
Разрыв 2-го рода. Точка 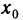
Пример:
Для функции 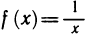
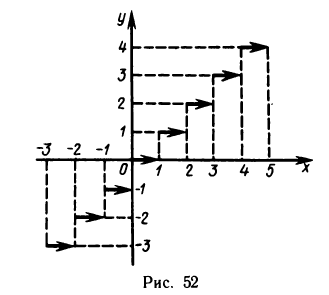
Кусочно-непрерывные функции
Функция f(х) называется кусочно-непрерывной на отрезке 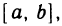
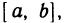
Функция называется кусочно-непрерывной на числовой прямой, если она кусочно-непрерывна на любом отрезке.
Пример:
Функция 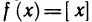
Основные свойства непрерывных функций
Теорема об устойчивости знака непрерывной функции
Теорема:
Пусть функция f(х) непрерывна в точке 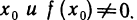
Доказательство:
Пусть 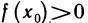

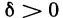
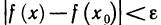
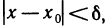
для всех 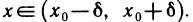
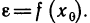
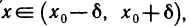
Если же 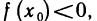
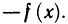
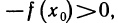
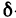
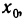
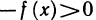
Рассмотрим теорему о прохождении непрерывной функции через нулевое значение при смене знаков.
Теорема:
Первая теорема Больцано — Коши. Пусть функция f(х) непрерывна на отрезке [а, b] и на концах отрезка имеет значения разных знаков. Тогда существует точка 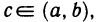
Доказательство:
Пусть для определенности 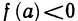
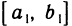
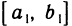
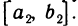
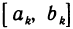
вложенных отрезков, причем 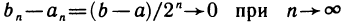
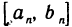
По теореме 2.13 о вложенных отрезках существует точка с, принадлежащая всем отрезкам. Докажем, что f(c)=0. Действительно, если допустить, что f(c)>0, то по теореме 4.8 об устойчивости знака непрерывной функции существует окрестность точки с, в которой f(x)>0. В эту окрестность при достаточно большом п попадет отрезок 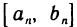
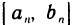
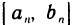
Доказанная теорема имеет простой геометрический смысл: непрерывная кривая при переходе из одной полуплоскости, границей которой является ось абсцисс, в другую пересекает эту ось.
Рассмотрим теорему о прохождении непрерывной функции через любое промежуточное значение.
Теорема:
Вторая теорема Больцано—Коши. Пусть функция f(х) непрерывна на отрезке [а, b], причем f(a) = A, f(b) = B. Пусть, далее, С — любое число, заключенное между А и В. Тогда на отрезке [а, b] найдется точка с такая, что f(c) = C.
Другими словами, непрерывная функция при переходе от одного значения к другому принимает и все промежуточные значения.
Доказательство:
Пусть для определенности А
По теореме 4.9 существует точка 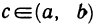
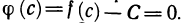
Следствие:
Если функция f(х) определена и непрерывна на некотором промежутке X, то множество ее значений Y также представляет собой некоторый промежуток.
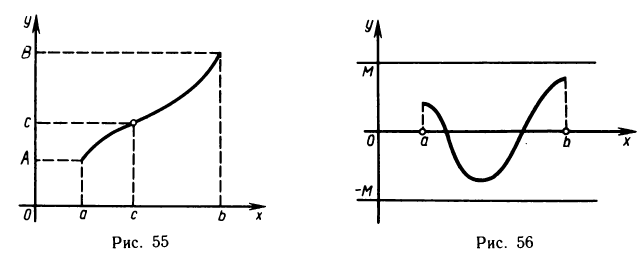
Прежде чем доказать это следствие, введем понятие точных граней функции. Пусть функция y = f(x) определена на множестве
X, а У—множество ее значений. Если множество У ограничено сверху (снизу), то оно имеет точную верхнюю (нижнюю) грань. Точная верхняя (нижняя) грань множества У называется точной верхней (нижней) гранью функции y=f(x) на множестве X и обозначается 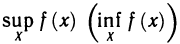
Первое из этих условий показывает, что число М(m) является одной из верхних (нижних) граней функции y=f(x) на множестве X, а второе условие показывает, что М(m) — наименьшая (наибольшая) из верхних (нижних) граней функции, т. е. точная грань.
Первое из этих условий показывает, что число М(m) является одной из верхних (нижних) граней функции y=f(x) на множестве X, а второе условие показывает, что М(m) — наименьшая (наибольшая) из верхних (нижних) граней функции, т. е. точная грань.
Если множество Y не ограничено сверху (снизу), то пишут 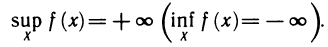
Докажем теперь следствие теоремы 4.10.
Доказательство:
Пусть
Возьмем любое у из У, не равное m и М, и выберем два значения 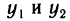
(если 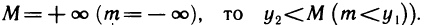
Теорема об ограниченности непрерывной функции на отрезка
Напомним, что функция f(х) называется ограниченной на отрезке 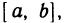
Теорема:
Первая теорема Вейерштрасса. Если функция f(х) определена и непрерывна на отрезке 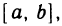
Предварительно докажем следующую лемму.
Лемма:
Функция f(х), непрерывная в точке 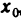
Доказательство:
Пусть 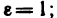

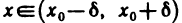
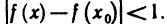
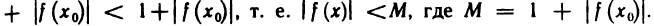
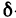
Доказательство теоремы. Предположим обратное, т. е. допустим, что функция f(х) неограниченна на отрезке [a, b]. Разделим отрезок [a, b] пополам, тогда, по крайней мере, на одном из двух полученных отрезков функция f(х) неограниченна (в противном случае она была бы ограничена на [a, b]). Обозначим этот отрезок через 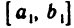
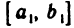
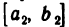
вложенных отрезков, на каждом из которых f (х) не ограничена, причем 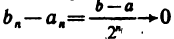
По теореме 2.1З о вложенных отрезках существует точка с, принадлежащая всем отрезкам. Функция f(х) по условию определена и непрерывна в точке с, следовательно, согласно доказанной лемме в некоторой окрестности точки с она ограничена. При достаточно большом п в эту окрестность попадет отрезок 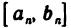
Замечание:
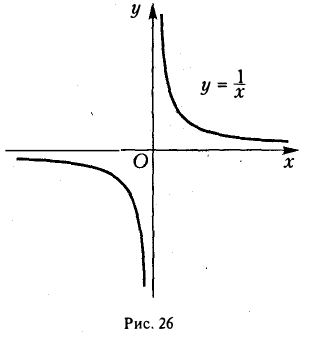
Теорема неверна, если отрезок [a, b] заменить интервалом (a, b). Так, например, функция f(х)=1/х непрерывна
На (0,1), но не ограничена, так как 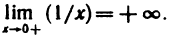
4. Теорема о достижении функцией, непрерывной на отрезке своих точных граней. В том случае, когда точные грани функции являются значениями функции, говорят, что функция достигает своих точных граней. Однако [см. формулу (1), гл. I, теорему 1.1] не всякому множеству принадлежат его точные грани. Следующий пример показывает, что точные грани функции не всегда достигаются.
Пусть на отрезке 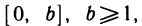
Установим, при каком условии функция достигает своих точных граней.
Теорема:
Вторая теорема Вейерштрасса. Если функция f(х) непрерывна на отрезке [a, b], то она достигает на этом отрезке своих точных граней, т. е. существуют точки 
Доказательство:
Так как функция f(х) непрерывна на отрезке [а,b], то по теореме 4.11 она ограничена на этом отрезке-Следовательно, согласно теореме 1.1 существуют точная верхняя М и точная нижняя m грани функции f(х) на отрезке [а,b].
Покажем, что функция f (х) достигает М, т. е. существует такая точка 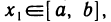
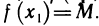
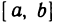
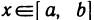

По теореме 4.7 функция F(х) непрерывна как частное двух непрерывных функций. В этом случае согласно теореме 4.11 функция F(х) ограничена, т. е. найдется положительное число ц такое, что для всех
Таким образом, число 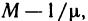
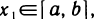
Аналогично доказывается, что функция f(х) достигает на [a, b] своей точной нижней грани m.
Замечание:
После того как доказано, что функция f(x), непрерывная на отрезке [a, b], достигает на этом отрезке своих точных верхней М и нижней т граней, можно назвать точную верхнюю грань максимальным значением, а точную нижнюю грань минимальным значением функции f(х) на этом отрезке и сформулировать теорему 4.12 в следующем виде: непрерывная на отрезке функция имеет на этом отрезке максимальное и минимальное значения.
Замечание:
Разность между наибольшим и наименьшим значениями непрерывной функции f(х) на отрезке [a, b] называется колебанием непрерывной функции на этом отрезке и обозначается буквой 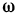
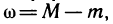
Понятие равномерной непрерывности функции
К числу других свойств функции, непрерывной на отрезке, относится очень важное свойство, называемое равномерной непрерывностью. Оно широко используется при доказательстве ряда фундаментальных теорем.
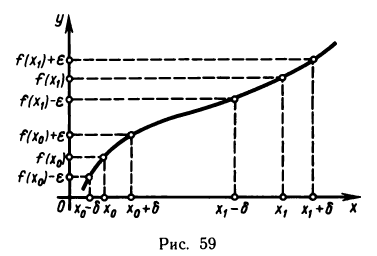
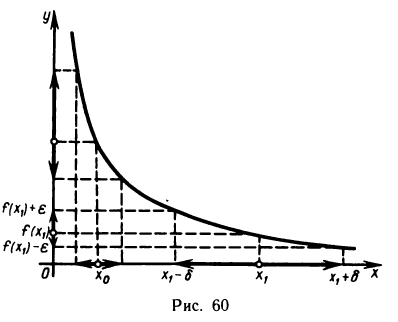
Пусть f(х) — функция, непрерывная на некотором промежутке X, и пусть точка 
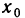


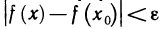
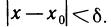
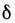
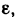
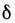
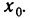
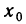
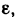
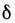
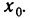
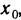
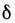
Таким образом, при заданном е каждой точке х рассматриваемого промежутка соответствует некоторое 
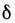
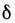
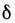
Возникает вопрос, существуют ли непрерывные функции, определенные на некоторых промежутках, для которых по любому е 

Определение. Функция f(х) называется равномерно-непрерывной на промежутке X, если для любого 

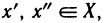
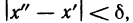
В логических символах это определение имеет вид
По самому определению, 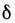
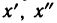
Следующая теорема устанавливает условие, при котором непрерывная функция является и равномерно-непрерывной.
Теорема о равномерной непрерывности функции
Теорема Кантора:
Если функция f(х) непрерывна на отрезке [а, b], то она и равномерно-непрерывна на нем.
Доказательство:
Докажем сначала, что если функция f(х) непрерывна на [а, b], то для любого 
Предположим обратное, т. е. допустим, что существует 
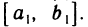
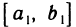
обладающих тем свойством, что ни один из них нельзя разбить на конечное число отрезков, на каждом из которых для любых двух точек х’ и х» будет выполняться неравенство 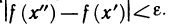
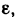
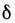
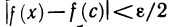
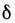
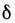
В 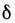
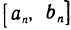
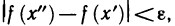
Перейдем теперь непосредственно к доказательству теоремы. По только что доказанному для любого 
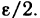
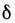
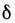
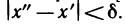
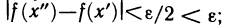
Таким образом, для любого 

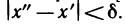
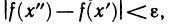
Следствие:
Пусть функция f(х) непрерывна на отрезке Тогда для любого 

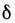
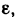
Замечание. Теорема неверна, если отрезок [a, ft] заменить интервалом или полуинтервалом.
Доказательство:
Действительно, по доказанной теореме функция f(x) равномерно-непрерывна на [а, b). Следовательно, для любого 

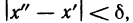
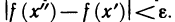
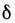
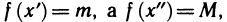
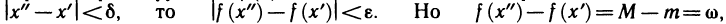
Пример:
Рассмотрим функцию 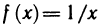


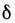
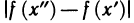
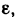
Понятие сложной функции
Определение:
Если на некотором промежутке X определена функция 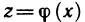
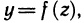
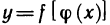
Пример:
Функция 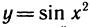
Теорема:
Пусть функция 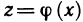
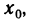
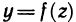
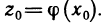
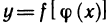
Доказательство:
Возьмем из X любую последовательность точек
сходящуюся к точке 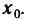
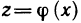
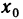
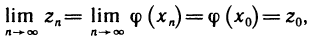
соответствующая последовательность точек 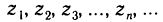
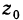
Следовательно, предел функции 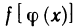
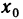
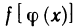
Пример:
Доказать непрерывность функции 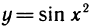
Решение:
Функция 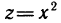
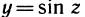
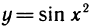
Понятие обратной функции
Определение обратной функции: Будем говорить, что функция f(x) не убывает (не возрастает) на множестве X, если для любых 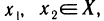

Неубывающие и невозрастающие функции объединяют общим названием монотонные функции.
Если для любых 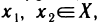

Примеры:
Функция 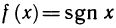
2. Функция f(х)=x является возрастающей на всей числовой прямой. Введем теперь понятие обратной функции.
Определение:
Пусть X и Y — некоторые множества и пусть задана функция f, т. е. множество пар чисел 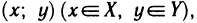
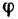
Обратную функцию будем обозначать символом
Отметим, что обратная функция, вообще говоря, не является Функцией, так как каждое число у может входить не только в одну, но и в несколько пар. Так, например, для функции у=х обратная Функция х=у — однозначна (каждое число у входит в одну пару), для функции 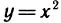
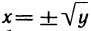
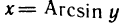
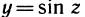
Из определения следует, что если обратная функция однозначна, т. е. является функцией в обычном смысле, то множество значений Y функции f является областью определения обратной функции 
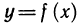
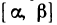
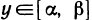
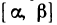
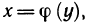
Таким образом, функция y=f(x) и обратная функция 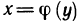
Если оси Ох и Оу поменять местами, для чего следует повернуть в пространстве плоскость Оху вокруг биссектрисы первого координатного угла на 180°, то новое положение графика обратной функции 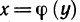
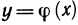
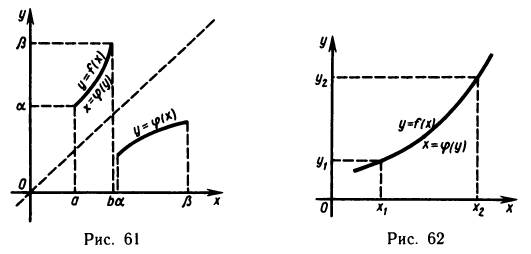
Теорема о непрерывности обратной функции
Теорема:
Пусть функция y=f(x) определена, строго монотонна и непрерывна на некотором промежутке X и пусть Y — множество ее значений. Тогда на множестве Y обратная функция 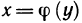
Доказательство:
Пусть для определенности функция f(х) возрастает на X, т. е. для любых 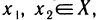

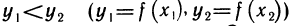
Однозначность обратной функции 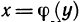
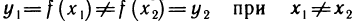
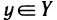
Докажем теперь, что обратная функция 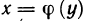

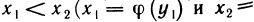
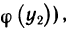
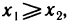
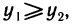
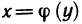
И наконец, покажем, что обратная функция 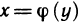
Пусть 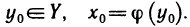
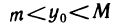
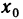

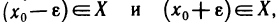
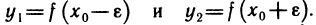
Возьмем теперь 
Тогда, если у удовлетворяет неравенствам
и, следовательно, в силу возрастания 
Таким образом, доказано что для любого достаточно малого 

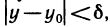
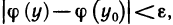
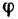
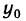
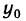
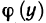
Если 
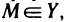
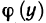
Итак, факт непрерывности обратной функции 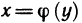
В случае убывания функции f (х) доказательство теоремы аналогично.■
Замечание. Если обратная функция 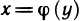
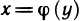
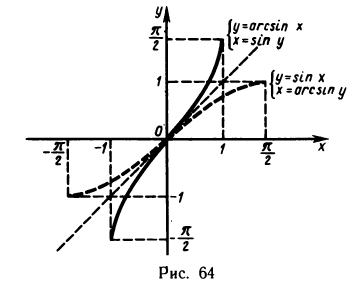
Пример:
Функция 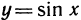
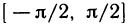
Эту обратную функцию обозначают 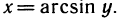
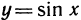
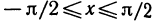
Если теперь х и у поменять местами, т. е. если рассматривать функцию у=arcsin х, то получится график, изображенный на рис. 64 сплошной линией.
Дополнение к функциям одной переменной
Если каждому элементу 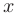
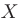
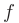
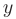
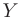
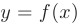
Переменная величина 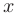
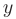
Множество 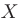
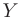
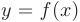
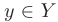
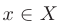
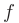
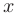
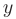
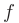
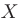
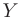
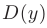
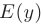
Графиком функции 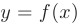
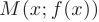
Функция 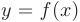
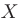
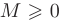
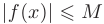
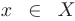
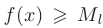
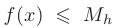
Если множество 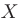
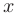
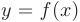
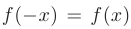
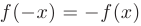
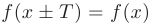
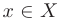
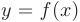
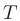
Чтобы определить функцию 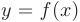
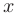
Аналитический способ определения функции является наиболее совершенным, так как позволяет не только сравнительно легко находить значения функции 
Используются также табличный и графический способы задания функции.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
Исследование функций одной переменной
Признаки возрастания и убывания функции
Определение:
Функция f(х), определенная на отрезке [а, b], называется неубывающей на [а, b], если для любых x1,x2 ∈ [а, b] из условия x1 f(x2), то функция f(х) называется убывающей на [а, b).
Определение:
Функция f(х) называется монотонной на [а, b], если она на [а, b] только неубывающая (в частности, возрастающая) или только невозрастающая (в частности, убывающая). Возрастающие и убывающие функции часто называют также строго монотонными.
Теорема:
Необходимость:
Учитывая, что по условию в каждой точке I интервала (а, b) существует производная f'(х), из последнего неравенства получим
Итак, в любой точке х ∈ (a, b) имеем f'(х) ≥ 0.
Достаточность:
Пусть f'(х) ≥ 0 на интервале (а, b). Докажем, что функция f(х) неубывающая на отрезке [а, b]. Действительно, пусть x1
Так как по условию f'(x) ≥ 0 в каждой точке х интервала (а, b),то и f'( ξ ) ≥ 0. Кроме того, x2 > x1. Поэтому
Итак, из неравенства x1 0 на интервале (а, b), то f(x) на отрезке [a, b] возрастает.
Однако если f(х) возрастает на [а, b], то отсюда не следует, что f'(х) > 0 всюду на интервале (а, b).
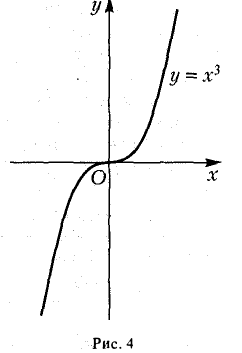
Пример:
Функция f(x) = х3 возрастает на отрезке (-1, 1), однако ее производная f'(x) = Зх2 обращается в нуль в точке х = 0-
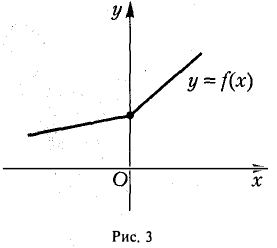
Принято говорить также о возрастании или убывании функции в точке.
Определение:
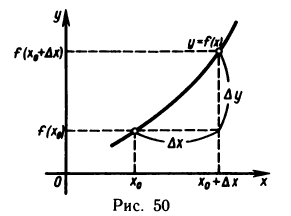
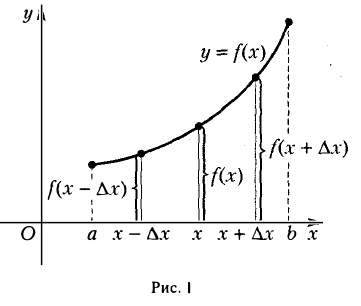
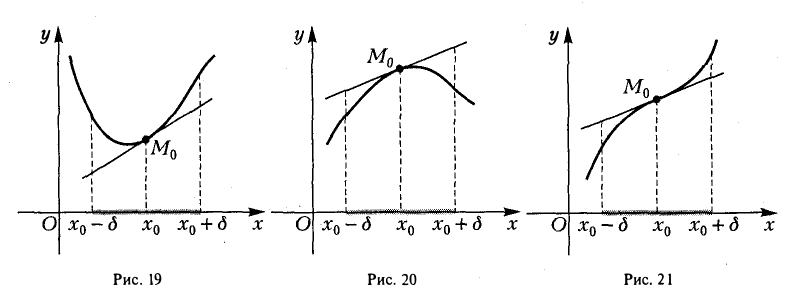
Функция/(х) называется убывающей в точке х = xo ecли в некоторой окрестности точки хо для всех х f(xо), а для всех х > хо имеем f(х) 0, то функция f(x) в точке Хо возрастает; если f'(x0) 0. Это означает, что
Но тогда существует такое δ > 0, что для всех ∆х, удовлетворяющих условию 0
Отсюда следует, что при 0 0, то и f(xо + ∆х) — f(хо) > 0, т. е.f(хо + ∆х) > f(х0). Согласно определению, это означает, что функция f(х) в точке хо возрастает.
Подобными рассуждениями можно доказать, что если f'(хо)
Экстремум функции
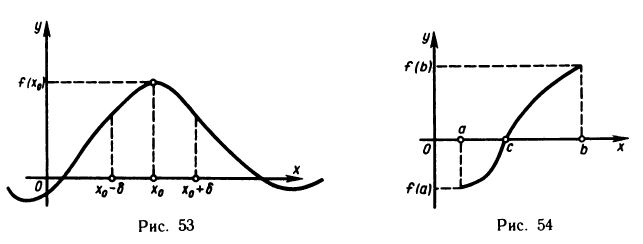
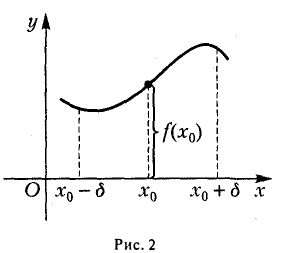
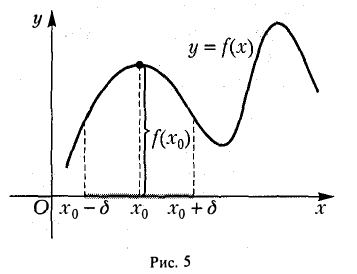
Пусть функция f(х) определена в некоторой окрестности точки хо, включая и саму точку хо.
Определение:
(рис.5). Если существует δ > 0 такое, что для всех х из интервала (хо — δ, хо + δ) верно неравенство
то точка х0 называется точкой локального минимума функции f(х) (рис.6).
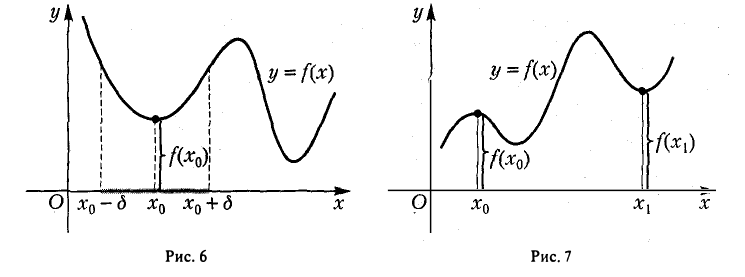
Значение функции f(х) в точке максимума называется локальным максимумом, значение функции в точке минимума — локальным минимумом данной функции. Максимум и минимум функции называются ее локальными экстремумами.
Термин локальный (относительный) экстремум обусловлен тем, что введенное понятие экстремума связано с окрестностью данной точки в области определения функции, а не со всей этой областью. Так, для функции у = f(х), график которой представлен на рис. 7, точка х0 есть точка локального максимума, а точка x1 — локального минимума, но f(х0) 0 такое, что для всех х, удовлетворяющих условию
верно строгое неравенство
В приведенном определении локального экстремума мы не предполагаем непрерывности функции f(х) в точке хо.
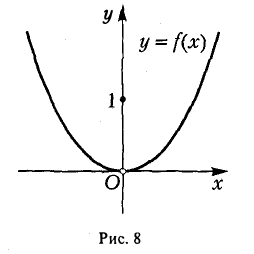
Пример:
разрывна в точке х = 0, но имеет в этой точке максимум. В самом деле, существует b > 0 (например, 6 1) такое, что для всех х ≠ 0 из интервала (-1,1) верно неравенство (рис. 8)
f(x) — f(0) = f(x) — 1
Задача:
Исходя из определения максимума и минимума, доказать, что функция
имеет в точке х = 0 минимум, а функция
не имеет в точке 1=0 экстремума.
Задача:
Исследовать на экстремум в точке хо функцию /(х) = (х-хо)п Необходимое условие экстремума
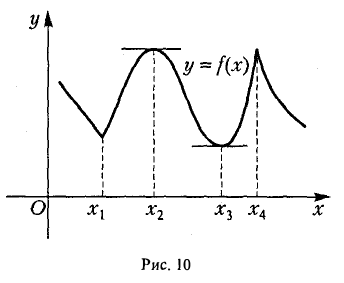
Теорема 4. Функция f(x) может иметь экстремум только в тех точках, в которых ее производная f'(x) либо равна нулю, либо не существует.
Аналогичными рассуждениями придем к тому же выводу при f'(xо)
Геометрическую иллюстрацию теоремы дает рис. 10. Функция у = /(х), график которой представлен на этом рисунке, имеет экстремумы в точках x1, x2, хз, x4; при этом в точках х1 и x4 производная f'(х) не существует, а в точках х2 и хз она равна нулю.
Точки, в которых выполняется необходимое условие экстремума для функции f(х), называются критическими точками этой функции. Они определяются как корни уравнения
f'(х) = 0
и как точки, где f'(х) не существует (в частности, где f'(x) — бесконечно большая функция). Корни уравнения f'(х) = 0 называют стационарными точками функции f(х): скорость изменения /(х) в такой точке равна нулю.
Теорема выражает лишь необходимое условие экстремума, и не в каждой своей критической точке функция f(x) обязательно имеет максимум или минимум.
Пример:
Так, например, для функции f(x) = х3 имеем f'(0) = 0. Поэтому точка х = 0 является критической для данной функции. Но функция f(x) = х3 в точке х = 0 экстремума не имеет, т.к. f(0) = 0, f(х) 0 для х > 0, так что в точке х = 0 данная функция возрастает.
Достаточные условия максимума и минимума
Теорема:
Теорема:
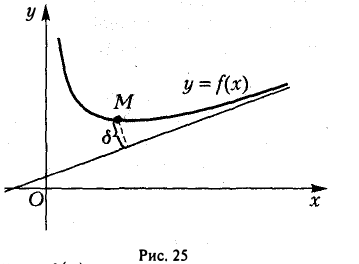
Пусть х = х0 есть критическая точка для функции f(х), т.е. либо f'(xо) = 0, либо f'(xо) не существует, но сама f(x) в точке хо непрерывна. Пусть существует такое δ > 0, что для всех х из интервала (хо — δ, xo) имеем f(x) 0, т. е. производная f'(х) при переходе х через точку хо меняет знак с минуса на плюс. Тогда точка хо есть точка минимума функции f(x).
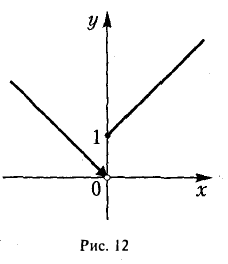
Условие непрерывности функции f(х) в самой точке х0 является существенным. Рассмотрим функцию
(рис. 12). В точке х = 0 производная f'(х) не существует. При переходе х через эту точку производная f'(x) меняет знак, но в точке х = 0 функция f(х) экстремума не имеет: не существует окрестности точки х = 0, в которой f0) = 1 было бы наибольшим или наименьшим значением функции f(x). Здесь нарушено условие непрерывности функции f(х) в точке х = 0.
Правило 1 (отыскания экстремумов функции). Чтобы найти точки максимума и минимума функции f(х), надо:
1) найти производную f'(x), приравнять ее к нулю и решить полученное уравнение f'(x) = 0;
2) найти точки, в которых производная f'(x) не существует. Эти точки и корни уравнения f'(x) = 0 будут критическими точками для функции f(x).
3) исследовать знак производной f'(x) слева и справа от каждой критической точки. Если при переходе х через критическую точку хо производная f(x) меняет свой знак с плюса на минус, то в точке х0 функция f(x) имеет максимум; если знак f'(x) меняется с минуса на плюс, то в точке хо функция f(x) имеет минимум. Если при переходе х через критическую точку xо знак f(x) не меняется, то в точке то функция f Примеры: 1) Находим производную: 2) Приравнивая у’ нулю, находим критические точки функции у(х): х = 0, х = 2. 3) Исследуем знак производной слева и справа от каждой из критических точек: Таким образом, точка х — 0 есть точка минимума, точка х = 2 — точка максимума данной функции (рис. 13). 2. Исследовать на экстремум функцию 1) Находим производную: 2) Производная нигде не обращается в нуль, но не существует в точке х = 0: 3> Исследуем знак у’ слева и справа от точки х = 0: Таким образом, точка х = 0 есть точка минимума данной функции (рис. 14). 3. Исследовать на экстремум функцию 2) Приравнивая у’ нулю, находим критические точки функции у(х): ч = 0. 3) Исследуем знак производной у’ слева и справа от точки х=0: Производная у'(х) = Зх2 > 0 как слева, так и справа от точки х = 0. Следовательно, в точке х = 0 экстремума нет, функция возрастает в точке х = 0. Замечание: Если функция f(х) имеет в точке хо экстремум, например, минимум, то это еще не значит, что справа отточки хо функция возрастает, а слева убывает. Это показывает следующий пример. Пусть функция f(х) задана равенством (рис. 15). Нетрудно видеть, что в точке х = 0 данная функция непрерывна и имеет минимум. Производная функции любой окрестности точки х = 0, исключая саму точку х = 0, непрерывна и меняет знак бесконечно много раз. А сама функция f(х) не монотонна ни слева, ни справа от точки х = 0. Следующая теорема опять выражает достаточные условия максимума и минимума функции. Теорема: Пусть в точке х0 функция f(х) имеет первую и вторую производные, причем f'(х0) — 0, a f»(х0) ≠ 0. Тогда в точке х0 данная функция f(x) имеет максимум, если f»(xо) 0. Пусть f»(х0) f'(x0) = 0, а для всех х из интервала (хо, xо + δ) верно f'(х) 0 то функция f(х) в точке х0 имеет минимум. Отсюда получаем второе правило отыскания точек экстремума функции. Правило 2 (отыскания экстремумов функции). Чтобы найти точки максимума и минимума функции f(х), надо найти критические точки f(х). Для этого поступаем так, как указано в правиле 1. Затем ищем вторую производную f»(х). Если она в критической точке х0 существует и меньше нуля: f»(хо) 0, то в точке хо функция f(х) имеет минимум. Если в критической точке xо вторая производная равна нулю или не существует, то такую точку xо можно исследовать с помощью первой производной. Пример: Исследовать на экстремум функцию откуда х = 0 — критическая точка. Если функция f(х) определена и непрерывна на отрезке [а, b], то, согласно второй теореме Вейерштрасса, она на этом отрезке принимает наибольшее и наименьшее значения. Если свое наибольшее значение М функция f(х) принимает во внутренней точке х0 отрезка [а, b], т. е. когда а Отсюда критические точки функции v(x): Находим вторую производную функцию v(x): При На концах отрезка [0, Таким образом, наибольшее значение функции v(x) — наибольшая вместимость коробки — будет, если выбрать Пусть дана кривая уравнением у = f(x) и пусть функция f(х) в точке хо имеет конечную производную f'(x0), т.е. в точке М0(х0,f(хо)) существует касательная к данной кривой, не параллельная оси Оу. Определение: Если существует такая окрестность (хо — δ,хо + δ) точки хо, что все точки данной кривой, абсциссы которых содержатся в этой окрестности, расположены над касательной к кривой в точке Мо, то говорят, что выпуклость данной кривой в точке Мо направлена вниз (рис. 19). Если все точки кривой с абсциссами из некоторой окрестности точки хо находятся под касательной к этой кривой в точке Мо, то говорят, что выпуклость данной кривой в точке Mo направлена вверх (рис. 20). Определение: Будем говорить, что график функции у = f(х), дифференцируемой на интервале (а, b), имеет на этом интервале выпуклость, направленную вверх (вниз), если график этой функции в пределах интервала (а, b) лежит не выше (не ниже) любой своей касательной. Определение: Точка Мo(хо, f(хо)) называется точкой перегиба кривой у = f(х), если существует окрестность (хо- δ, xо + δ) точки хо такая, что для х хо — в противоположную (рис.21). Очевидно, что если у — Y > 0 для всех х ≠ х0 в достаточно малой окрестности точки хо, то выпуклость кривой в точке Мo направлена вниз, а если у — Y Пусть функция у = f(х) в окрестности точки хо имеет производную второго порядка, непрерывную в точке хо. Воспользовавшись формулой Тейлора, будем иметь Из формул (1) и (2) получаем Если f»(х0) ≠ 0, то в силу устойчивости знака непрерывной функции в достаточно малой окрестности точки х0 знак f»[xо + θ ⋅ (х — хо)] совпадает со знаком f»(х0). Таким образом, из равенства (3) следует, что знак разности y-Y совпадает со знаком f»(хо). Поэтому, если f»(хо) >0, то у-У>0 для всех точек х ≠ х0, достаточно близких к точке хо, и в точке Мо(хо,f(х0)) выпуклость кривой у = f(х) направлена вниз, а если f»(хо) Теорема: Точка М0(хо, f(хо)) может быть точкой перегиба кривой у = f(х) только если f»(хо) = 0 (или f»(xо) не существует). Это условие не является достаточным. Так, например, для функции f(х) = х 4 имеем f»(x) = 12х 2 и f»(0) = 0, но точка 0(0,0) не есть точка перегиба кривой у = х 4 : в этой точке выпуклость кривой направлена вниз (рис. 24). Достаточный признак точки перегиба выражается следующей теоремой Теорема: Пусть функция f(х) имеет вторую производную в некоторой окрестности точки xo, непрерывную в точке хo. Если f»(xо) = 0 и при переходе х через точку х0 вторая производная f»(x) меняет знак, то точка Мо(х0, /(хо)) есть точка перегиба кривой y = f(x). Если же f»(х0) = 0, но в некоторой окрестности точки х0 знак f»(x) один и тот же как при х хо, то точка Мо не будет точкой перегиба: в этой точке выпуклость кривой направлена вниз, если f»(х) > 0 как слева, так и справа отточки х0, и выпуклость кривой направлена вверх, если f»(х) Очевидно, нет ни одной точки, в которой f»(х) = 0. Но есть точка х = 0, в которой f»(х) не существует. Касательная в точке O(0,0) к этой кривой перпендикулярна оси Ох. Окончательно достаточный признак точки перегиба может быть сформулирован так. Пусть кривая у = f(х) имеет в точке Мо(хо, f(х0)) касательную, хотя бы и параллельную оси Оу. Пусть функция f(х) в некоторой окрестности точки xo, кроме, быть может, самой точки х0, имеет непрерывную вторую производную. Если f»(x) в точке х0 равна нулю или не существует и при переходе х через точку хо производная f»(x) меняет свой знак, то точка Мо(х0,f(хо)) есть точка перегиба кривой у =f(х). Определение: Асимптотой кривой с бесконечной ветвью называется такая прямая, что расстояние δ точки М кривой до этой прямой стремится к нулю при неограниченном удалении точки М по бесконечной ветви от начала координат (рис. 25). Прямая х = х0 является вертикальной асимптотой графика функции у = f(x), если хотя бы одно из предельных значений Так, график функции у = 1/x имеет вертикальную асимптоту x = 0, поскольку Кривая у = На рис. 27 представлены возможные случаи взаимного расположения кривой и вертикальной асимптоты. Для разыскания вертикальных асимптот кривой у= f(x) поступаем так: 1) находим на оси Ох точки разрыва функции f(x) 2) выделяем те из них, в которых хотя бы один из пределов функции f(х) (слева или справа) равен + ∞ или — ∞. Пусть это будут точки x1, х2, …., хт. Тогда прямые х = х1, х = x2…,х = хт будут вертикальными асимптотами графика функции у = f(x). Вертикальная прямая х = х0 может оказаться асимптотой графика функции у = f(x) и в том случае, когда точка х0 является концом интервала, в котором определена функция f(x). Это будет тогда, когда хо — левый конец интервала и либо когда хо — правый конец интервала и Например, функция у = ln х определена в интервале 0 так что прямая х = О (ось Оу) является вертикальной асимптотой графика функции у=In х. Пусть функция у = f(x) определена для всех х ≥ а (или х ≤ а). И пусть прямая у = kх + b является асимптотой графика функции у = f Для определенности будем рассматривать сколь угодно большие значения аргумента х положительного знака. Тот факт, что прямая у = kx + b является асимптотой кривой у = f(x), означает, согласно определению асимптоты, что расстояние δ от точки М(х, f(x)) кривой до этой прямой стремится к нулю при х —» + ∞. Обозначим через а (а ≠ т. е. когда функция f(x) представима в виде Существование асимптоты у = kх + b у кривой у = f(х) при х —> + ∞ означает, что при х —> +оо функция y = f(х) ведет себя «почти как линейная функция», т.е. отличается от линейной функции у = кх + b на бесконечно малую функцию при х —> + ∞. Теорема: Для того, чтобы график функции у = f(х) имел при х —> + ∞ наклонную асимптоту у = kх + b, необходимо и достаточно, чтобы существовали оба предела Необходимость.: Пусть график функции у = f(х) при х —> + ∞ имеет асимптоту у = kх + b, т. е. для f(x) справедливо представление (1): т. е. существуют оба предела (2). Достаточность: Это означает, что график функции у = f(х) имеет наклонную асимптоту у = kх + b. Аналогично исследуется случай х → — ∞. Пример: Рассмотрим функцию Ее график имеет вертикальную асимптоту х = 1. Запишем функцию Величина Отсюда следует, что график данной функции имеет наклонную асимптоту у = х + 1 (рис. 30). Полезно исследовать знак разности ∆ = f(x) — kх — b. Если ∆ > 0, то кривая расположена над асимптотой; если ∆ Горизонтальная асимптота (частный случай наклонной, k = 0) Если при х → + ∞ (или при х → — ∞ ) функция f(x) имеет конечный предел, равный числу b: то прямая у = b есть горизонтальная асимптота соответственно для правой или левой ветви графика функции у = f(x). Примеры: 2. Пусть у = arctg x. Для функции f(x) = arctg x имеем Таким образом, правая ветвь графика функции у = arctg х имеет горизонтальную асимптоту у = 3. Пусть у = прямая у = 0 является горизонтальной асимптотой графика функции у = Последний пример показывает, что кривая у = f(x) может пересекать свою асимптоту, и даже бесконечное множество раз. Задача: Установить условия существования асимптот у графика рациональной функции. Одна из возможных схем исследования функции и построения ее графика разлагается на следующие этапы решения задачи: Пример: Построить график функции (вeрэиера или локон Марии Аньези). В таблице стрелка Пример: Построить график функции 1. О.О.Ф. — вся числовая ось, исключая точку х = 0. 2. Точка разрыва функции х = 0. Имеем так что прямая x = 0 — вертикальная асимптота. 3. Функция не является ни четной, ни нечетной (функция общего положения); непериодическая. наклонных и горизонтальных асимптот нет. откуда х = График функции изображен на рис. 34. Пример: Построить график функции 1. О.О.Ф. — полупрямая х > 0. 2. В области определения функции точек разрыва нет. При х —» 0 + 0 имеем так что прямая 1=0, проходящая через граничную точку области определения функции у(х), является вертикальной асимптотой графика функции. 3. Функция общего положения, непериодическая. 4. Полагая у = 0, получаем х + Отсюда у = x — наклонная асимптота графика. Из рис. 36 видно, что х2+1 > In x ∀x > 0 и, значит у’ > 0 ∀x, т. е. функция f(x) возрастает на (0, + ∞). Экстремумов нет. Вторая производная обращается в нуль при х = е3/2, и при переходе х через эту точку у» меняет знак с « — » на « + ». Следовательно, х = е3/2 — абсцисса точки перегиба кривой. Результаты исследования сводим в таблицу: График функции изображен на рис. 37. Построить график функции 1. О.О.Ф. — вся числовая ось, исключая точку х = 0. 3. Функция общего положения, непериодическая. Следовательно, график функции имеет наклонную асимптоту у = х. Из условия у’ = 0 получаем х3 — 2 = 0, т. е. х = 7. Поскольку у» = Результаты исследования сводим в таблицу: График функции изображен на рис. 38. Пример: Построить график функции 1. О.О.Ф. — вся числовая ось. 2. Непрерывна всюду. Вертикальных асимптот нет. 3. Общего положения, непериодическая. 4. Функция обращается в нуль при х = 0 и 1 = 3.5. Таким образом, график функции имеет наклонную асимптоту у = х — 2. Производная у'(х) обращается в нуль в точке х = 1 и не существует при х = 0 и х = 3. При переходе х через точку х = 0 (х 1) производная у'(х) меняет знак с « — » на « + », т. е. в точке х = 3 функция имеет минимум. 7. Находим вторую производную Результаты исследования сводим в таблицу: График функции представлен на рис. 39. Для отыскания точек максимума и минимума функций может быть использована формула Тейлора. Теорема: Пусть функция f(x) в некоторой окрестности точки xq имеет производную п-го порядка, непрерывную в точке xo. Пусть f'(x0) = f»(x0) =… = f(n-1)(xо) = 0, но f(n)(xо) ≠ 0. Тогда если число п — нечетное, то функция f(x) в точке х0 не имеет экстремума; когда же п — четное, то в точке х0 функция f(x) имеет максимум, если f(n)(xо) 0. В силу определения точек максимума и минимума вопрос о том, имеет ли функция f(x) в точке х0 экстремум, сводится к тому, существует ли такое δ > 0, что в интервале (хo — δ, хо + δ) разность f(x) — f(x0) сохраняет знак. По формуле Тейлора Так как по условию По условию f(n)(х) непрерывна в точке f(n)(хо) ≠ 0. Поэтому в силу устойчивости знака непрерывной функции существует такое δ > 0, что в интервале (хо — δ, xo + δ) знак f(n)(x) не меняется и совпадает со знаком f(n)(хо). Рассмотрим возможные случаи: 1) п — четное число и f(n)(хо) > 0. Тогда Согласно определению это означает, что точка хо есть точка минимума функции f(х). 2) п — четное и f(n)(xо) вместе с этим и f(х) — f(хо) ≤ 0 ∀x ∈ (хо — δ, Хо + δ). Поэтому точка хо будет в этом cлучае точкой максимума функции f(х). 3) п — нечетное число, f(n)(xо) ≠ 0. Тогда при х > хо знак будет совпадать со знаком f(n)(xо), а при х 0 знак разности f(х) — f(xо) не будет одним и тем же для всех х ∈ (хо — δ, хо + δ). Следовательно, в этом случае функция f(х) в точке xо экстремума не имеет. Пример: Рассмотрим функции 1) у = x4; 2) у = х3. Легко видеть, что точка х = 0 является критической точкой обеих функций. Для функции у = хx первая из отличных от нуля производных в точке х = 0 есть производная 4-го порядка: x(4)(0) = 24 > 0. Таким образом, здесь п = 4 — четное и x(4)(0) > 0. Следовательно, в точке х = 0 функция у = х4 имеет минимум. Для функции у = х3 первая из отличных от нуля в точке х = 0 производных есть производная 3-го порядка. Так что в этом случае п = 3 — нечетное, и в точке х = 0 функция у = х3 экстремума не имеет. Замечание: С помощью формулы Тейлора можно доказать следующую теорему, выражающую достаточные условия точки перегиба. Tеорема: Пусть функция /(х) в некоторой окрестности точки х0 имеет производную п-го порядка, непрерывную в точке х0. Пусть Простейший пример доставляет функция f(x) = х3. Задача состоит в нахождении действительного корня уравнения f(x)= 0. (1) Предположим, что выполнены следующие условия: 1) функция f(x) непрерывна на отрезке [а, b]; 2) числа f(а) и f(b) противоположны по знаку: f(а) • f(b) Точка a1, в которой хорда АВ пересекает ось Ох, расположена между а и ξ и является лучшим приближением к ξ чем а. Полагая в (2) у = 0, найдем Из рис. 41 нетрудно заметить, что точка а1 будет всегда расположена с той стороны от ξ в которой знаки f(х) и f»(x) противоположны. Проведем теперь касательную к кривой у = f(х) в точке B(b, f(b)), т. е. в том конце дуги АВ, в котором f(х) и f»(x) имеют один и тот же знак. Это существенное условие: без его соблюдения точка пересечения касательной с осью Ох может вовсе не давать приближение к искомому корню. Точка b1, в которой касательная пересекает ось Ох, расположена между ξ и b с той же стороны, что и b, и является лучшим приближением к ξ чем b. Касательная эта определяется уравнением Полагая в (3) у = 0, найдем b1: Таким образом, имеем Пусть абсолютная погрешность приближения ξ* корня ξ задана заранее. За абсолютную погрешность приближенных значений а1 и b1 корня ξ можно взять величину |b1 — а1|. Если эта погрешность больше допустимой, то, принимая отрезок [a1, b1] за исходный, найдем следующие приближения корня ξ Продолжая этот процесс, получим две последовательности приближенных значений Последовательности <аn>и Можно показать, что если выполнены сформулированные выше условия 1)-3), то а = β = ξ — единственному корню уравнения f(x) = 0. Пример: Найти корень ξ уравнения х2 — 1 = 0 на отрезке [0,2]. Результат очевиден: ξ = 1. Попытаемся его получить методом хорд. Функция f(х) = x2 — 1 1) непрерывна на отрезке [0, 2]; что дает приближение к точному значению корня ξ с абсолютной погрешностью ∆( ξ ‘) Функция одной переменной и её вычисление Понятие числовой функции: Определение: Пусть даны два множества действительных чисел X и У. Числовой функцией у = f(x) называется правило, которое каждому числу х ∈ X ставит в соответствие единственное число у ∈ Y. Переменную х называют независимой переменной или аргументом, переменную у — зависимой переменной или функцией, множество X называется областью определения D(f), множество Y называется областью изменения или множеством значений функции E(f). Наряду с обозначениями функции у = f (x) используются и другие, в частности у =у (х). Значение функции для фиксированного значения аргумента x₀ будем обозначать y₀ = f(x₀) или y₀ = y(x₀). Сама функция, ее аргумент и значение могут быть обозначены и другими буквами, например: V = F(u). Если переменные х и у рассматривать как декартовы координаты точек на плоскости, то графиком числовой функции у = f(x) называется множество точек координатной плоскости Oxy с координатами (x; f(x)). Основными способами задания функции являются аналитический, графический и табличный. При аналитическом способе функция задается посредством формул. При этом она может быть задана в декартовых и полярных координатах в явном и неявном виде, в параметрическом виде. Если в уравнении, определяющем функцию, значение функции у выражено в явном виде (изолировано в левой части уравнения), то говорят, что функция задана в явном виде: Пример: Данная функция, заданная в явном виде, каждому действительному числу х ∈ R ставит в соответствие единственное действительное число у, для получения которого необходимо значение х умножить на 2 и к результату прибавить 1. Область определения данной функции D(f) = (-∞;+∞), область изменения E(f) = (-∞;+∞). Если в уравнении, определяющем функцию, значение функции у не выражено в явном виде (не изолировано в левой части уравнения), то говорят, что функция задана в неявном виде уравнением вида: Заметим, что при этом остается требование, чтобы каждому числу х из области определения соответствовало единственное значение у из множества значений. Так, например, уравнение x² + y² = R² определяет две функции: у = Пример: Функция задана уравнением в неявном виде. Для каждого действительного значения х ≠ 0 существует единственное значение у, удовлетворяющее этому уравнению. Область определения этой функции D(f) = (-∞; 0) ⋃ (0; +∞), область изменения E(f) = (—∞; 0) ⋃ (0; +∞). При графическом способе функция задается с помощью графика. Например, по графику функции, изображенному на рис. 26, можно установить, что значению х = 0 соответствует единственное значение у = 1, значению х = 1 соответствует единственное значение у = 2 и т. д. При параметрическом задании функции в декартовых координатах значение функции у и ее аргумента х задаются как функции от третьей переменной величины, так называемого параметра t из множества Т: Если эти функции вычислить при одном и том же значении параметра t, мы получим координаты точки на плоскости M(x;y); когда переменная t пробегает все значения из множества Т, точка M(x,y) описывает некоторую линию в плоскости Оху. Уравнения ( 3.1) называются параметрическими уравнениями этой линии. Иногда, исключив параметр t из системы ( 3.1), можно получить явное или неявное уравнение функции. Пример 3.3. Если эти уравнения почленно возвести в квадрат и сложить, то в силу тождества sin²t + cos²t = 1 получится уравнение x² + y² = R². Этому уравнению удовлетворяют координаты точек окружности с центром в начале координат и радиусом R, так как в силу формулы ( 2.6) для точек М(х,у), координаты которых удовлетворяют этому уравнению, расстояние до начала координат 0(0; 0) постоянно и равно R. Если из уравнения x² + y² = R² выразить у в явном виде, получим две элементарные функции: у = Пример: Эти уравнения называются параметрическими уравнениями циклоиды. Можно показать, что линия, описываемая этими уравнениями (циклоида), получается как траектория фиксированной точки M окружности радиусом а, касавшейся в начальный момент оси абсцисс в начале координат, которая катится без скольжения по оси абсцисс (рис. 27). При этом в начальный момент точка M совпадает с началом координат. При изменении параметра t от 0 до 2π окружность совершит один полный оборот. Точка M при этом опишет одну арку циклоиды. При этом каждому значению Пример: r = a(1+ cos Кривая, описываемая этим уравнением в полярных координатах, называется кардиоидой (рис. 28). Составив таблицу для некоторых значений полярного угла При табличном способе функция задается посредством таблицы. Например, следующая таблица устанавливает закон, который каждому из перечисленных в этой таблице значений аргумента х ставит в соответствие единственное значение у. Пример: Найти область определения и область изменения функции у = Решение: Так как операция извлечения квадратного корня определена только для неотрицательных величин, то данная функция определена только для значений аргумента х, удовлетворяющих неравенству: 2x-1 ≥ 0. Решая это неравенство, получаем: D(f) = [0,5;+∞). Поскольку арифметический корень не может быть отрицательным, заключаем, что область изменения E(f) = [0; +∞). Пример: Найти область определения и область изменения функции Решение: Поскольку областью определения логарифмической функции является бесконечный интервал (0; +∞), заключаем, что область определения D(f) = <x∣x² — 3x + 2 >0>. Решим это неравенство, для чего определим корни уравнения: Областью значений логарифмической функции является множество R, поэтому E(f) = <y∣y ∈ R>. Пример: Найти область определения функции у = Решение: Пример: Найти область определения функции у = Решение: Допустимые значения аргумента х удовлетворяют неравенству 1 — х² > 0. Решая это неравенство, находим, что D(f) = (-1;1). Пусть даны две функции: у = f(x) и у = g(x) с областью определения D(f) и D(g) соответственно. Тогда можно определить новую функцию у = f(x) + g(x), значения которой при каждом х из области определения вычисляются как сумма значений f(x) и g(x). Область определения функции у = f(x) + g(x) есть D(f) ∩ D(g). Аналогично определяются функции у = f(x)g(x), у = f(x)- g(x) и у = Пример: Найти область определения функции у = Решение: Представим нашу функцию в виде у = f(x) + g(x), где f(x) = Область определения исходной функции есть пересечение этих множеств. Пусть u = f(x) — числовая функция с областью определения D(f) и областью изменения E(f), а у = g(u) — числовая функция с областью определения D(g), E(f) ⊂ D(g) и областью изменения E(g). Тогда каждому х ∈ D(f) соответствует единственное значение у ∈ Е(g) : каждому х ∈ D(f) функция u= f(x) ставит в соответствие единственное значение u ∈ E(f), которому функция у = g(u) ставит в соответствие единственное значение у ∈ Е(g). Полученная функция называется сложной функцией (или суперпозицией двух функций) и обозначается y = g(f(x))∙ Функция u = f (х) называется внутренней функцией, функция у = g(u) — внешней. Например, если u = х² — Зх + 2, и у = log₂ и, то можно определить сложную функцию у = Iog₂ (х² — Зх + 2). Пример: Записать сложную функцию, являющуюся суперпозицией двух функций: u = 1 — x² и у = В данном примере f(x) = 1 — х² ⇒ D(f) = R, E(f) = (-∞ ;1], g(u) = Ответ: у = Определение: Определение: Числовая функция у = f(x) называется четной, если область ее определения симметрична относительно начала координат и f(-x) = f(х) для всех х ∈ D(f). График четной функции симметричен относительно оси ординат, т.к. точки (x;f(x)) и (-x;f(-x)) для четной функции симметричны относительно оси Оу, поскольку f(-x) = f(x)- Например, функция у = x² + 1 является четной, поскольку D(f) = (-∞;+∞) симметрична относительно начала координат и f(-x) = (-х)² + 1 = x² + 1 = f(х). График функции у = x²+1 симметричен относительно оси Oy (рис. 29). Сумма, разность, произведение и частное двух четных функций есть четная функция. Попробуйте доказать это самостоятельно Определение: График функции у = х³ симметричен относительно точки О ( рис. 30). Сумма и разность нечетных функций есть нечетная функция. Доказательство этих утверждений проводится аналогично тому, как это было сделано для четных функций: сначала устанавливается симметричность области определения, затем проверяется справедливость требуемого равенства. Докажите их самостоятельно. Наряду с четными и нечетными существуют функции, не являющиеся ни теми, ни другими, т.е. не обладающие свойством четности-нечетности. Например, функции у = x³ + 1, у — √х, у = Заметим, что любую функцию у = Пример: Функция у = √х не является ни четной, ни нечетной, т. к. ее область определения D(f) = [0; +∞) не является симметричной относительно О. Пример: Является ли функция Решение: Область определения этой функции Ответ: у = Пример: Решение: Область определения этой функции Проверим выполнение одного из равенств: Ответ: у = Функция у = f(x) называется периодической с периодом T ≠ 0, если х — T и х + T принадлежат области определения, f(x) = f(x ± Т) для любого х ∈ D(f). Обычно под периодом функции понимают наименьший из всех положительных периодов, если такой период существует. В этом случае все периоды T кратны наименьшему периоду T₀ : T = n ∙ T₀, где n ∈ Z. Из определения следует, что T₀ > 0. Пример: Функция у = sin x имеет период T₀ = 2π, т.к. х + 2π ∈ D(f), х — 2π ∈ D(f) и sin (x ± 2τr) = sin x. Пример: Сумма, разность, произведение и частное периодических функций с периодом T является периодической функцией с периодом Т. Например, у = Например, у = sin² х является периодической функцией с периодом T₀ = π. В пункте 5.2 лекции 5 будет показана справедливость следующего утверждения: Теорема: Если функция у = f(х) периодическая с периодом Т, то функция у = Kf(kx + b) + а будет также периодической с периодом T₁ = Пример: Найти период функции у = 2sin(3x + 2). Решение: у = sin х имеет период T = 2π, k = 3. Поэтому период T₁ функции у = 2sin(3x + 2) будет равен T₁ = Пример: Решение: Эта функция не является периодической, т. к., например, для х=0 и Т>0 х- T не принадлежит области определения. При T Ограниченные функции Определение: Функция у = f(x) называется ограниченной сверху, если существует такое число М, что для всех х ∈ D(f) выполняется неравенство: f(x) ≤ М. Функция у = f(x) называется ограниченной снизу, если существует такое число т, что для всех х ∈ D(f) выполняется неравенство: f(x) ≥ т. Функция, ограниченная сверху и снизу, называется просто ограниченной. Определение: Функция у = f(x) называется возрастающей на множестве X ⊂ D(f), если для любых x₁ ∈ X и x₂ ∈ X из неравенство x₁ > x₂ следует f(x₁) > f(x₂) (т.е. ’’чем больше х, тем больше у”), функция у = f(x) называется убывающей на множестве X ⊂ D(f), если для любых x₁ ∈ X и x₂ ∈ X из неравенства x₁ > x₂ следует f(x₁) x₂ следует f(x₁) ≥ f(x₂)∙ Функция у = f(x) называется невозрастающей на множестве X ⊂ D(f), если для любых x₁ ∈ X и x₂ ∈ X из неравенства x₁ > x₂ следует f(x₁) ≤ f(x₂) ∙ Функции только возрастающие или только убывающие, называются монотонными, а соответствующие множества X — областями монотонности. Например, функция у = х² на (-∞;0] убывает, а на [0; +∞) возрастает. Пример: Доказать возрастание функции у = √x. Решение: D(f) = [0;+∞). Возьмем x₁ > x₂ > 0 два значения аргумента из области определения. Необходимо доказать, что f(x₁) > f(x₂). Рассмотрим разность f(x₁) — f(x₂) — √x₁ — √x₂. Умножим и разделим на сумму корней: Пример: Функция, изображенная на рис. 91, возрастает на интервалах Определение: Если функция у = f(x) обратима, то можно каждому значению у ∈ E(f) поставить в соответствие единственное число х ∈ D(f). Такое обратное соответствие называют функцией, обратной κ y = f(x) и обозначают х = f⁻¹(y). Аргумент обратной функции обычно обозначают через х, а значения функции через у. Тогда обратная функция запишется в виде: y = f⁻¹ (x). Если функция f⁻¹ является обратной по отношению к f, то f⁻¹ является обратимой, и f является обратной по отношению к f⁻¹. Функции f и f⁻¹ называют взаимно обратными. Для взаимно обратных функций имеют место следующие равенства: Функция является обратимой тогда и только тогда, когда каждое свое значение она принимает только один раз. В частности, периодические и четные функции не являются обратимыми. Графики взаимно обратных функций симметричны относительно прямой у = х ( рис. 32), что является следствием замены х на у и у на х. Примем без доказательства следующую теорему. Теорема: Если у = f(x) возрастающая (убывающая) непрерывная функция, то она имеет обратную, которая тоже является возрастающей (убывающей). Функция, обратная нечетной, также нечетная. Пример: Найти обратную функцию к функции у = 2х — 1. Построить графики обеих функций. Решение: Выразим значение х через у : у = 2x — 1 ⇔ х = Функция у = х², как отмечалось, необратима, однако если ее рассматривать только при х ∈ [0; +∞), то она будет монотонной и, следовательно, обратимой. График обратной функции у = √х изображен на рисунке 34 Определение: Основными элементарными функциями являются: постоянная функция (у = с), степенная (у = xⁿ,n ∈ R), показательная (у = Определение: Элементарными функциями называются те функции, которые можно задать в явном виде одним аналитическим выражением из основных элементарных функций с помощью арифметических операций и нахождения функции от функций, примененных конечное число раз. Примерами элементарных функций являются многочлены, дробно-рациональная функция (отношение двух многочленов), иррациональные (корень из элементарной функции) и т. д. Не являются элементарными, например, функции: Рассмотрим свойства некоторых элементарных функций. Определение: Линейной функцией называется функция вида: Из изложенного следует, что уравнение ( 4.5) описывает любую прямую на плоскости, кроме вертикальной. Действительно, если две точки лежат на вертикальной прямой, то x₁ = x₂ и в уравнении ( 4.5) k = Определение: Пучком прямых, проходящих через данную точку (х₀;y₀), называется множество всех прямых на плоскости, проходящих через данную точку. Из сказанного следует, что однопараметрическое уравнение всех прямых пучка, кроме вертикальной, имеет вид (4.6). Уравнение конкретной прямой пучка получается из ( 4.6) при фиксированном k. Наряду с уравнением ( 4.1) прямая на плоскости может быть задана так называемым общим уравнением прямой: Действительно, уравнение ( 4.1) легко записать в виде ( 4.7), перенеся все члены в левую часть. Наоборот, если В ≠ 0 в уравнении ( 4.7), то выражая у, получаем уравнение у = Определение: Обратной пропорциональной зависимостью называется функция вида: у = Функция неограниченная, непериодическая. Функция нечетная т.к. D(f) симметрична относительно точки О и f(-х) = Докажем последнее утверждение. Возьмем x₁ > x₂ > 0 и рассмотрим f(x₁)-(x₂) = 4.5. Степенная функция у = хⁿ. Рассмотренные функции у = х, у = х², у = Показательная функция у = Логарифмическая функция у = logₐ х, a > 0, α ≠ 1. Поскольку функция у = Iogₐ х является обратной к функции у = D(f) — (-∞;+∞), E(f) = [-1;1] Функция ограничена —1 ≤ cos x ≤ 1. Функция четная, т.к. D(f) симметрична относительно О и f(-x) = cos(-x) = cos x = f(x). Функция периодическая с периодом T = 2π. Функция не монотонная: убывает на (2πn; π + 2πn) и возрастает на (π + 2πn; 2π + 2πn), n ∈ Z. Точки пересечения с осью Ох: ( График функции у = cos x изображен на рис. 42. Функция необратимая, но если рассмотреть ее на [0; π], то существует обратная функция у = arccos х. Функция периодическая с периодом T = π. Функция не монотонная; возрастает на(- Точки пересечения с осью Ox: (πn; 0); n ∈ Z, точка пересечения с осью Оу: (0;0). График функции у = tg х изображен на рис. 43 Функция необратимая, но если рассмотреть ее на ( Функция нечетная, т.к. D(f) симметрична относительно О и f(-x) = ctg(-х) = — ctgx = —f(x). Функция периодическая с периодом T = π. Функция не монотонная; убывает на (πn; n + πn), n ∈ Z. Точки пересечения с осью Ох: ( График функции у = Ctg х изображен на рис. 44. Функция необратимая, но если рассмотреть ее на (0; π), то существует обратная функция у = arcctg х. Свойства этих функций получаются из свойств тригонометрических функций на основании п. 3.8 Функция ограничена: — Функция нечетная: arcsin(-х) = — arcsin х. Функция возрастает на области определения. Точка пересечения с осями: (0;0). График функции изображен на рис. 45. Функция ограничена: 0 ≤ arccosx ≤ π. Можно показать, что arccos(-х) = π — axccos х. Функция убывает на области определения. очка пересечения с осью Ох: (1;0); с осью Оу: (0; График функции изображен на рис. 46. Функция ограничена: — Пример: Найдите область определения функции: Решение: Область определения данной функции есть пересечение областей определения функций у = √-x т.е.-х ≥ 0 и Таким образом, область определения искомой функции есть решение системы неравенств: Пример: Найдите область определения функции у = arcsin (x + 1) Решение: Область определения данной функции есть множество решений системы неравенств: Решая данную систему, получаем: Пример: Исследуйте функцию на четность и нечетность: y= Решение: Область определения данной функции D(f) = (-∞ ; +∞) симметрична относительно начала координат. Проверим выполнение второго условия: f(-х) = Пример: Исследуйте функцию у = x² — 5x + 6 на четность и нечетность. Решение: Область определение этой функции есть (-∞ ;+∞), симметрична относительно 0. Проверим выполнение второго условия: Следовательно, данная функция свойствами четности, нечетности не обладает. Заметим, что ее можно представить в виде суммы четной (у = x² + 6) и нечетной (у = —5х) функций. Пример: Для приведенной функции найдите наименьший положительный период T, если она периодическая: у = 5 sin 3x. Решение: Период функции у = sin х равен 2π. В соответствии с теоремой п.3.5 наименьший положительный период функции у = 5sin3x будет равен Пример: Найдите наименьший положительный период функции у = 3 sin 5x + 4 cos 7х. Решение: В соответствии с теоремой 3.1 функция у = 3 sin 5х будет периодической с периодом T₁ = Пример: Для данной функции определите область, в которой она будет обратимой, и найдите обратную функцию: у = 2х + 3. Решение: Данная линейная функция монотонно возрастает при х ∈ R, поэтому обратима. Для нахождения обратной функции выразим х через у и затем обозначим х через у а у через х: у = 2x + 3 ⇔ х = Пример: Пусть f(x) = Решение: Подставим в искомую функцию у = Пример: Найдите уравнение прямой, удовлетворяющей следующим условиям: прямая проходит через точку M (1; 1) под углом 135° к оси Ох. Решение: Пример: Вычислите углы треугольника, стороны которого даны уравнениями: l₁ : 18x+6y-17 = 0, l₂ : 14x-7y+15 = 0, l₃ = 5x+10y-9 = 0. Решение: Пример: Найдите координаты вершины А в Δ ABC, стороны которого даны уравнениями: AB : у — х, AC : у = —х + 4, BC : у = 5х — 4. Решение: Найдем координаты вершины А как решение системы уравнений: Пример: Решение: Линейная функция имеет вид f(x) = kх + b. Подставив данные значения аргумента и функции, получаем систему уравнений для нахождения неизвестных параметров k и b: Ответ: Пример: Напишите условия, задающие множество точек Δ ABC, если A(l;l), В(2;3), C(3;0). Решение: Напишем уравнение сторон Δ ABC, используя уравнение прямой, проходящей через две точки. Прямая AB делит плоскость Oxy на две полуплоскости: у ≥ 2x — 1 и у ≤ 2х — 1. Δ ABC расположен в той из них, в которой находится вершина С. Поскольку координаты точки C(3;0) удовлетворяют второму из приведенных неравенств, заключаем, что Δ ABC лежит в полуплоскости, удовлетворяющей неравенству у ≤ 2х — 1. Решение заданий и задач по предметам: Дополнительные лекции по высшей математике: Образовательный сайт для студентов и школьников Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника. © Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического институтаИсследование функций на максимум и минимум при помощи второй производной
Прежде всего заметим, что точка х0 является критической точкой для данной функции f(x), т. к. f'(xо) = 0.Наибольшее и наименьшее значение функции, непрерывной на отрезке
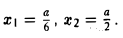
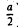
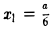
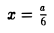
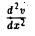
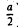
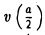
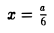
Направление выпуклости и точки перегиба кривой
Иными словами, точка Мo — точка перегиба кривой, если в этой точке кривая переходите одной стороны касательной на другую, меняя направление выпуклости.Асимптоты графика функции
Вертикальные асимптоты
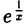
Наклонные асимптоты
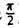
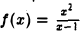
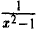
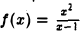
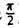
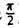
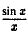
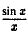
Схема построения графика функции
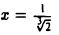
Вторая производная функции у» = 2 + 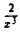
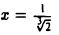
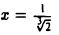
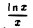
Пример: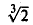
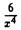
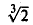
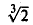
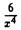
Исследование функций на экстремум с помощью производных высшего порядка
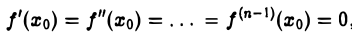
Вычисление корней уравнений методами хорд и касательных
y = f(x).
F(x,y) = 0.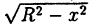
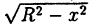
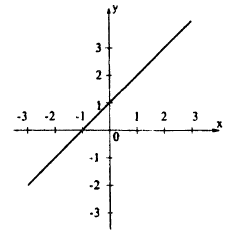
(3.1)
(3.2) 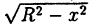
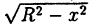
(3.3) 
При задании функции в явном виде в полярных координатах полярный радиус г выражается через полярный угол 
(3.4) r = r(



0 π /4 π /2 3π /4 π 5π /4 3π /2 7π /4 2π r 2a a 0 a 2a x -2 -1 -0,5 0 1 y -3 -1 0 1 3 
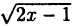
y = log₂(x² — 3x + 2).
x² — 3x + 2 = 0 ⇒ x₁ = 1, х₂ = 2. Следовательно, решением неравенства x²- Зх + 2 > 0 является (- ∞; 1) ⋃ (2; +∞).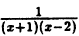
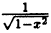
Операции над функциями
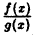
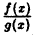
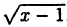
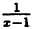
D(f) : х — 1 ≥ 0 ⇔ D(f) = [1;+∞),
D(g) : х — 1 ≠ 0 ⇔ D(g) = (-∞; 1) U (1; +∞).Сложная функция
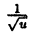
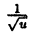
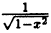
Четные и нечетные функции
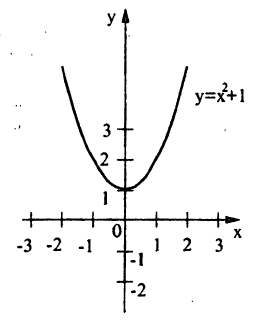
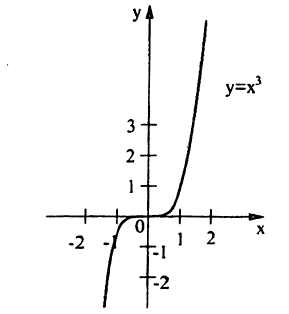
Произведение и частное нечетных функций есть четная функция.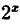


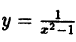
D(f) = (-∞ ;0) ⋃ (0; +∞) симметрична относительно О.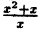
D(f) = (-∞; —1) ⋃ (-1; 1) ⋃ (1; +∞) симметрична относительно О.
f(-x) = f(x) или f(-x) = —f(x).
f(-х) = 
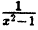
Периодичность функции
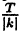
Ответ: T₁ = 
Возрастание и убывание функций
√x₁ — √x₂ = 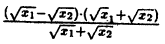
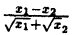
Т.к. x₁ > x₂ ⇔ x₁ — x₂ > 0 ⇔ 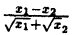
⇔ f(x₁) — f(x₂) > 0 ⇔ f(x₁) > f(x₂)- Утверждение доказано.
(a; x₁), (x₂, x₃), (x₄, b) и убывает на интервалах (x₁; x₂), (x₃, x₄).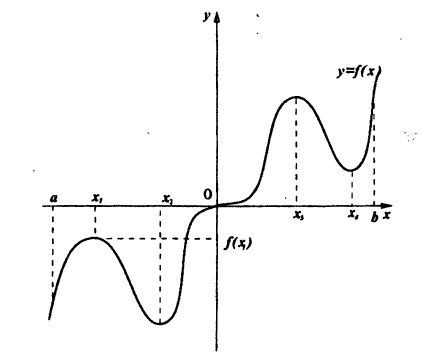
Обратные функции
D( f⁻¹) = E(f)-, f⁻¹ (f(x)) = х для x ∈ D(f)∙, E( f⁻¹) = D(f), f( f⁻¹(x)) = х для х ∈ D( f⁻¹).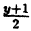
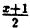
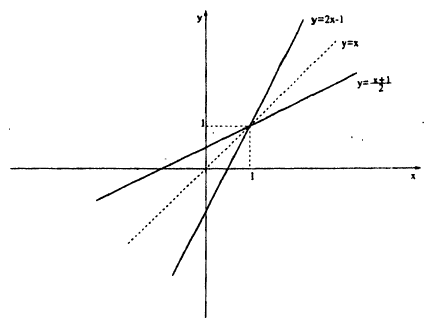
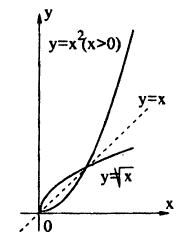
Элементарные функции. Свойства основных элементарных функций
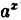
и т. д.Линейная функция. Прямая на плоскости
(4.1) у = kх + b.
D(f) = (-∞;+∞); при k ≠ 0 E(f) = (-∞;+∞), функция неограничена, непериодическая. При b = 0 функция нечетная; при k > 0 функция возрастает, при k 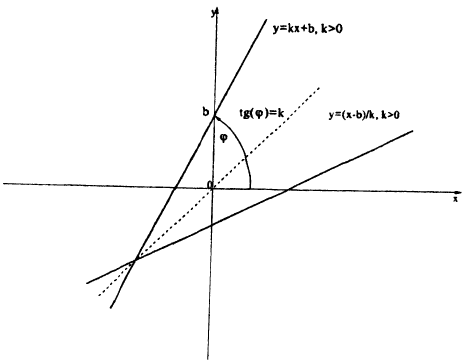
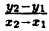


(4.6) у — y₀= k(x — х₀).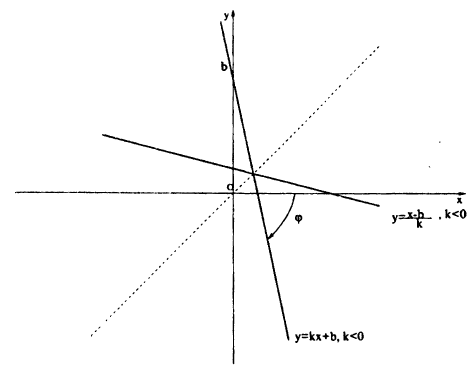
(4.7) Ax + By + C = 0,
где коэффициенты А и В не равны нулю одновременно.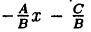
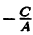
Обратная пропорциональная зависимость
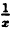
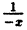
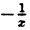
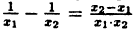
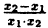
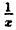
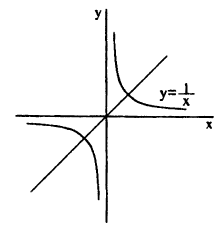
Показательная функция
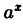
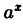
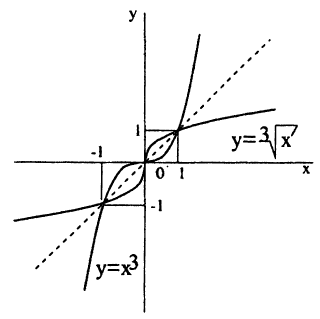
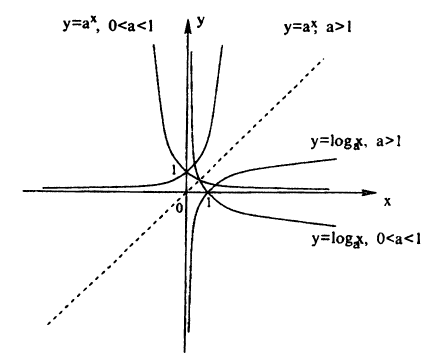
Тригонометрические функции
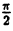
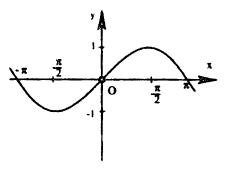
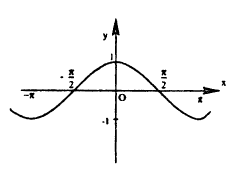
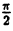
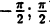
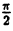
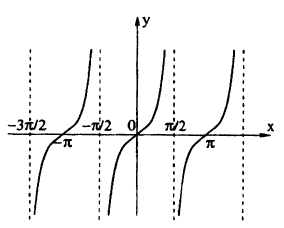
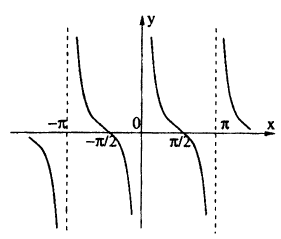
Обратные тригонометрические функции
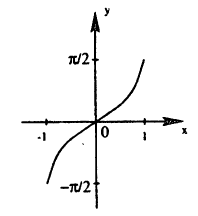
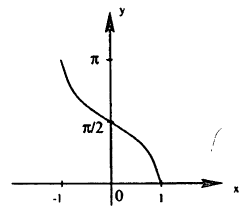
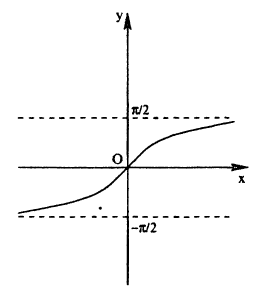
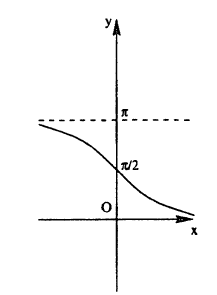
Решение заданий на тему: Функция одной переменной
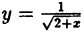
Ответ: четная.
f(—х) = (-x)² — 5(-x) + 6 = x² + 5x + 6≠ ±f(х)
Ответ: четностью, нечетностью не обладает.
Ответ: 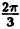
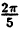
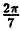
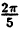
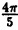
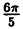
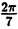
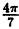
Ответ: T = 2π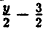
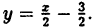
Ответ: Множество, на котором функция обратима: R. Обратная функция 
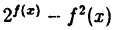
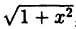
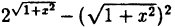
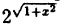
Ответ: