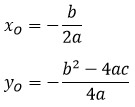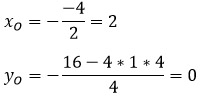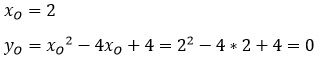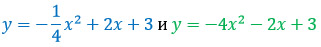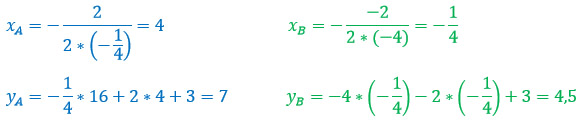Что такое график квадратичной функции
Квадратичная функция.
Обратите внимание: коэффициент a может быть любым действительным числом, кроме нуля. Действительно, если a = 0, то ax 2 + bx + c = 0·x 2 + bx + c = 0 + bx + c = bx + c. В этом случае в выражении не остаётся квадрата, поэтому его нельзя считать квадратным трёхчленом. Однако, такие выражения-двучлены как, например, 3x 2 − 2x или x 2 + 5 можно рассматривать как квадратные трёхчлены, если дополнить их недостающими одночленами с нулевыми коэффициентами: 3x 2 − 2x = 3x 2 − 2x + 0 и x 2 + 5 = x 2 + 0x + 5.
Если стоит задача, определить значения переменной х, при которых квадратный трёхчлен принимает нулевые значения, т.е. ax 2 + bx + c = 0, то имеем квадратное уравнение.
Если существуют действительные корни x1 и x2 некоторого квадратного уравнения, то соответствующий трёхчлен можно разложить на линейные множители: ax 2 + bx + c = a(x − x1)(x − x2)
Замечание: Если квадратный трёхчлен рассматривать на множестве комплексных чисел С, которое, возможно, вы еще не изучали, то на линейные множители его можно разложить всегда.
Когда стоит другая задача, определить все значения, которые может принимать результат вычисления квадратного трёхчлена при различных значениях переменной х, т.е. определить y из выражения y = ax 2 + bx + c, то имеем дело с квадратичной функцией.
При этом корни квадратного уравнения являются нулями квадратичной функции.
Квадратный трёхчлен также можно представить в виде
Это представление удобно использовать при построении графика и изучении свойств квадратичной функции действительного переменного.

Графиком квадратичной функции является парабола, вершина которой находится в точке 
Парабола обладает еще одним интересным свойством, которое также используется как её определение.
Парабола представляет собой множество точек плоскости, расстояние от которых до определенной точки плоскости, называемой фокусом параболы, равно расстоянию до определенной прямой, называемой директрисой параболы.
Построить эскиз графика квадратичной функции можно по характерным точкам.
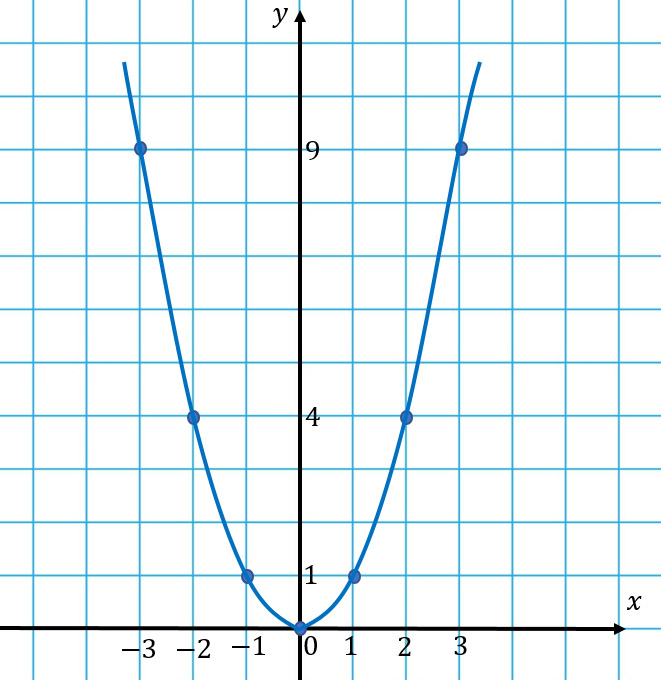
Например, для функции y = x 2 берем точки
| x | 0 | 1 | 2 | 3 |
| y | 0 | 1 | 4 | 9 |
Соединяя их от руки, строим правую половинку параболы. Левую получаем симметричным отраженим относительно оси ординат.
Для построения эскиза графика квадратичной функции общего вида в качестве характерных точек удобно брать координаты её вершины, нули функции (корни уравнения), если они есть, точку пересечения с осью ординат (при x = 0, y = c) и симметричную ей относительно оси параболы точку (−b/a; c).
| x | −b/2a | x1 | x2 | 0 | −b/a |
| y | −(b 2 − 4ac)/4a | 0 | 0 | с | с |
| при D ≥ 0 | |||||
Производная квадратичной функции вычисляется по формуле (ax 2 + bx + c)’ = 2ax + b.
Формулы для такого перехода можно выучить наизусть, а можно научиться выделять полный квадрат из трёхчлена с заданными коэффициентами. Это умение весьма полезно также для решения некоторых уравнений и неравенств, для вычисления интегралов и т.д.
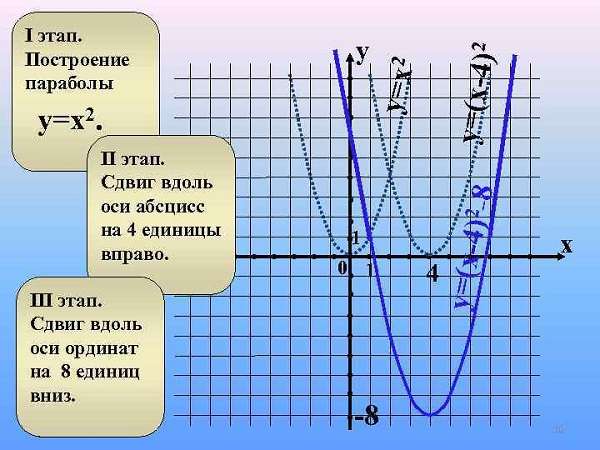
Итак, чтобы построить график функции y = 3x 2 − 5x + 2 из графика y = x 2 нужно последний сдвинуть по оси Ox вправо на 5/6 ≈ 0,83 единицы. Затем растянуть вдоль оси Oy в 3 раза и, наконец, опустить по оси Oy на 1/12 ≈ 0,08 единицы.
Посмотрите, что получилось.
Если Вы являетесь моим учеником или подписчиком, то можете поработать с интерактивными версиями этих графиков.
Преобразуем выражение с выделением полного квадрата: 
Строим график функции 
Видеоуроки с параболой.
Графики квадратичной функции и коэффициенты квадратного трёхчлена.
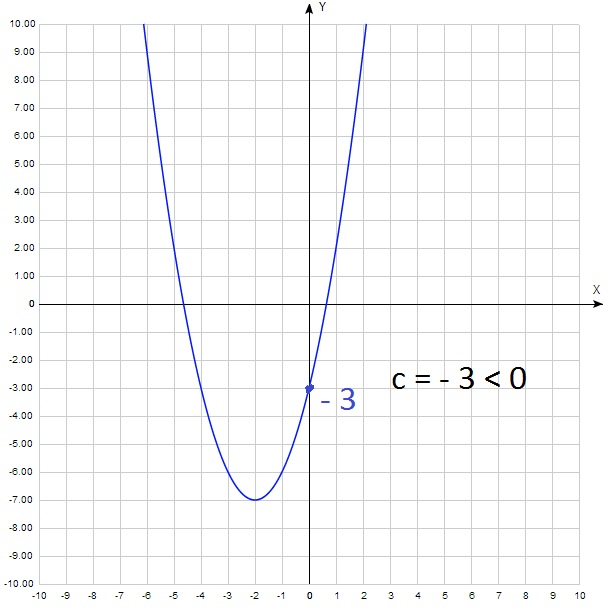
Положение и вид параболы в зависимости от знака и значения параметра c.
Построение параболы по характерным точкам.
Быстрое построение параболы как графика квадратичной функции.
Другие случаи. Примеры построения.
Задачи на анализ графика квадратичной функции.
Задания вида «Установить соответствие между коэффициентами квадратного трёхчлена и приведенными графиками квадратичной функции» встречаются в ОГЭ по математике в 9-ом классе, а также необходимы сдающим ЕГЭ за 11 класс в качестве промежуточного действия.
Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.
Квадратичная функция и её график
Парабола является графиком квадратичной функции, которая задается формулой y = ax 2 + bx + c.
Нарисовать параболу можно, используя таблицу значений, в которой мы выбираем произвольный х и находим у. Но не всегда этот способ является самым рациональным.
Начнем, как всегда, с простого)
Стандартная парабола.
На координатной плоскости отмечаем эти точки и чертим параболу.
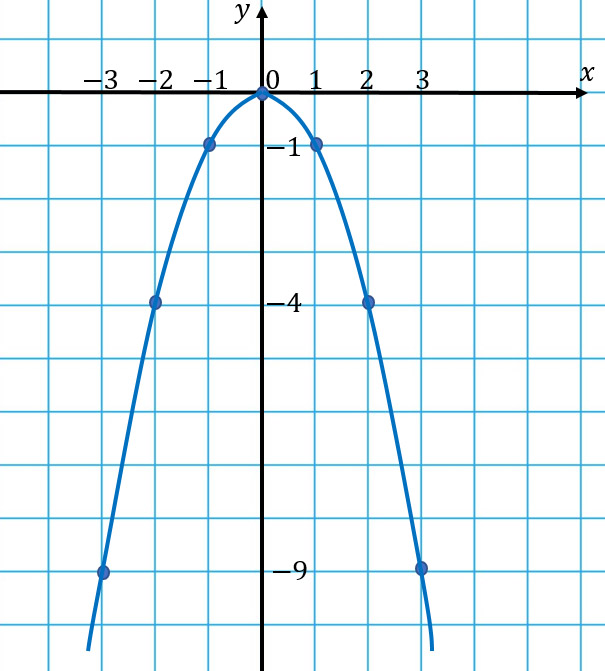
Начало координат тоже является вершиной этой параболы, как и в предыдущем случае, но ветви уже будут направлены вниз:
Если у тебя черный пояс по рисованию стандартных парабол, то следующий раздел пройдет у тебя «на ура».
Параболы со смещенной вершиной.
Зачем я начала статью со стандартной параболы? Ответ прост. Графиком любой квадратичной функции y = ±x 2 + bx + c (обязательно коэффициент перед х 2 должен равняться ±1) является стандартной параболой, только вот вершины этих парабол не будут находится в начале координат.
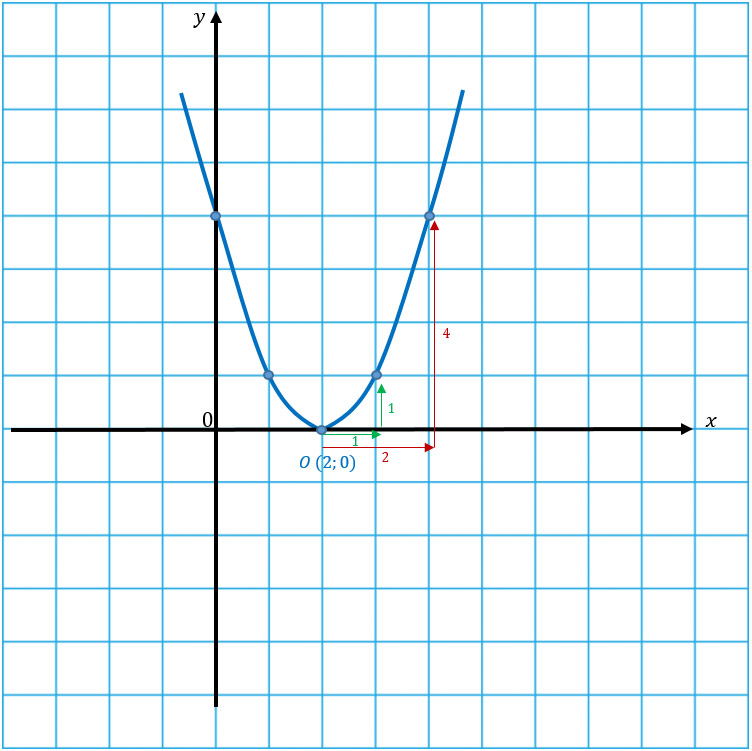
Чтобы начертить подобные параболы нужно сначала узнать, где находится вершина.
Пусть вершиной параболы будет точка О с координатами (x1; y1). Тогда найти эти координаты можно по формулам:
Кстати, можно найти координаты вершины и другим способом.
Координату хО находим по той же формуле, а координату уО можно найти подстановкой координаты хО в функцию.
Без примера не обойтись)
Найдем сначала вершину параболы двумя способами, чтобы убедится, что оба способа рабочие.
1 способ: по формулам.
2 способ: подстановкой.
Одну координаты мы уже нашли по формуле. Подставляем ее в исходную функцию.
Параболы-стройняшки и параболы-пухляшки.
Удивительно, но числовой коэффициент перед х 2 оказывается влияет на стройность и полноту парабол.
Если числовой коэффициент лежит в промежутке (-1; 0) ∪ (0; 1), то парабола будет более обширно смотреться на координатной плоскости.
Не веришь? Давай проверим! Для примера возьмем две функции:
К сожалению, здесь схитрить не получится: обе параболы нестандартные и для обеих необходимо создать таблицы значений. Но перед эти определимся с их вершинами.
Переходим к таблицам значений.
| x | 0 | 2 | 4 | 6 | 8 |
| y | 3 | 6 | 7 | 6 | 3 |
| x | -1,5 | -1 | -0,25 | 0 | 1 |
| y | -3 | 1 | 4,5 | 3 | -3 |
Чертим обе параболы по получившимся координатам.
Вот о чем я и говорила) Перед тобой парабола-стройняшка и парабола-пухляшка во всей красе.
Практикум по параболам.
Теорию о параболах можно еще писать и дальше, но тебя, скорее всего, интересует практика по графикам.
Поскольку речь идет о параболах, то с параболами мы и будем сейчас возиться.
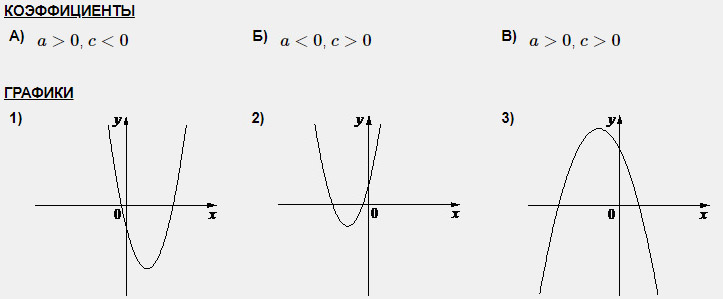
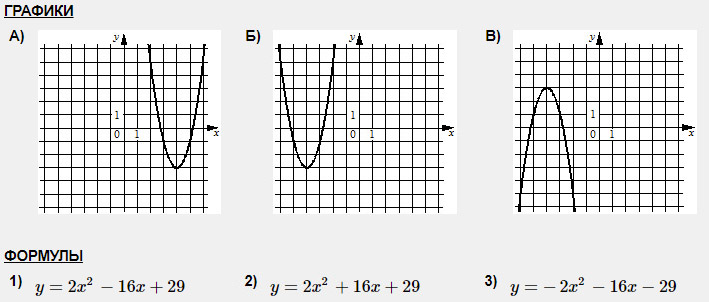
Задание 1. На рисунке изображены графики функций вида y = ax 2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
А) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с отрицателен, то график пересекает ось Оу ниже нуля. Подходит график 1.
Б) Если коэффициент а отрицателен, то ветви направлены вниз; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 3.
В) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 2.
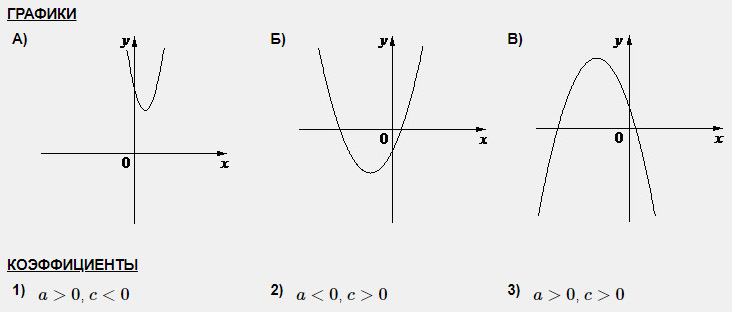
Задание 2 (наоборот). На рисунке изображены графики функций вида y = ax 2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
А) Ветви направлены вверх, значит а > 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 3.
Б) Ветви направлены вверх, значит а > 0; график пересекает ось Оу ниже нуля, значит и с 0. Подходит вариант под номером 2.
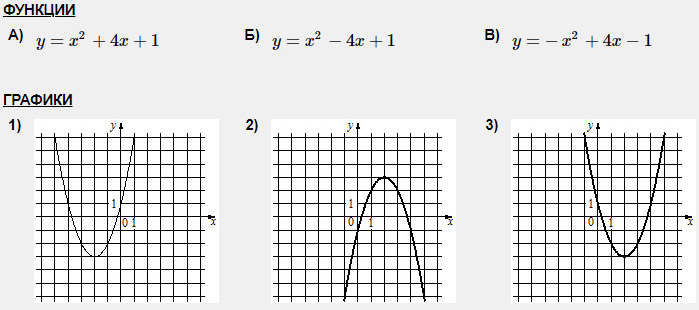
Задание 3. Установите соответствие между графиками и их функциями.
Дальше рекомендую отработанную годами технику. Она минимизирует твои ошибки, если ты, конечно, умеешь считать)
Задание 4 (наоборот, но принципе тот же). Установите соответствие между функциями и их графиками.
На графике 1 выбираем точку. Вершина снова четкая, но для разнообразия давайте возьмем другую точку, например, точку с координатами (-4; 1). Будь внимателен и смотри, чтобы точно такой же точки не было на третьем графике!
Что такое график квадратичной функции
Задания на свойства и графики квадратичной функции вызывают, как показывает практика, серьезные затруднения. Это довольно странно, ибо квадратичную функцию проходят в 8 классе, а потом всю первую четверть 9-го класса «вымучивают» свойства параболы и строят ее графики для различных параметров.
Это связано с тем, что заставляя учащихся строить параболы, практически не уделяют времени на «чтение» графиков, то есть не практикуют осмысление информации, полученной с картинки. Видимо, предполагается, что, построив десятка два графиков, сообразительный школьник сам обнаружит и сформулирует связь коэффициентов в формуле и внешний вид графика. На практике так не получается. Для подобного обобщения необходим серьезный опыт математических мини исследований, которым большинство девятиклассников, конечно, не обладает. А между тем, в ГИА предлагают именно по графику определить знаки коэффициентов.
Не будем требовать от школьников невозможного и просто предложим один из алгоритмов решения подобных задач.
Посмотрим, как влияют на внешний вид параболы знаки ее коэффициентов.
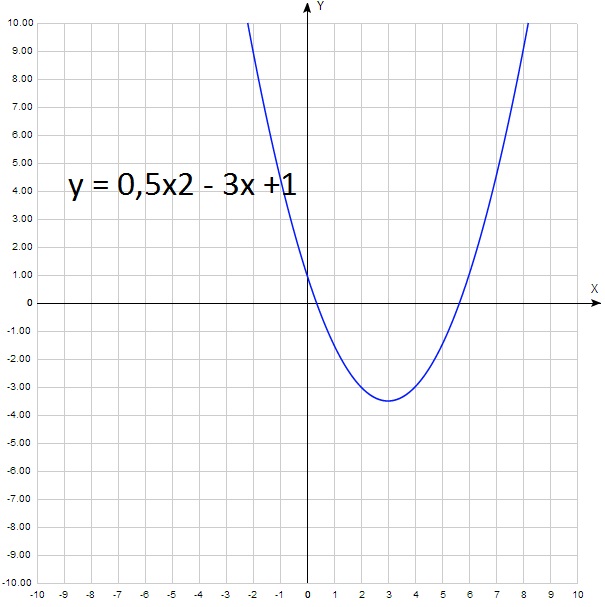
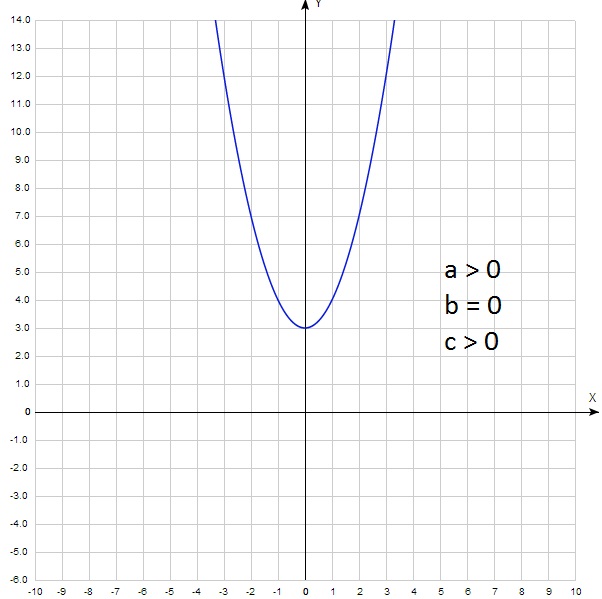
Самая простая зависимость для коэффициента а. Большинство школьников уверенно отвечает: » если а > 0, то ветви параболы направлены вверх, а если а 0.
В данном случае а = 0,5
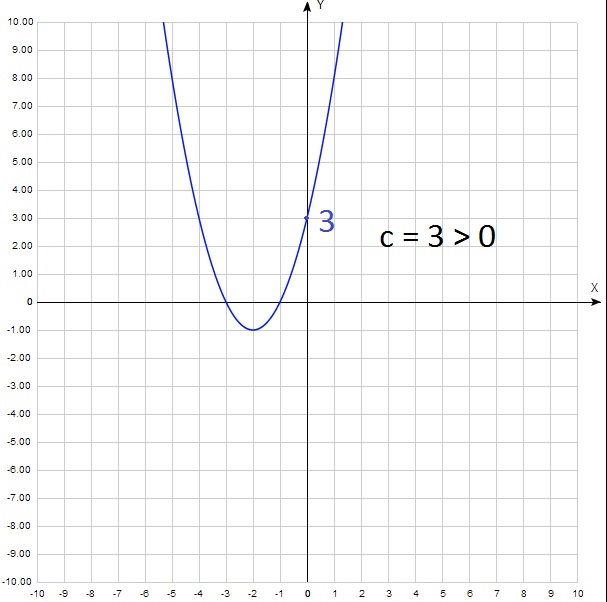
А теперь для а 2 + b 0 + c = c. Получается, что у = с. То есть с – это ордината точки пересечения параболы с осью у. Как правило, эту точку легко найти на графике. И определить выше нуля она лежит или ниже. То есть с > 0 или с 0:
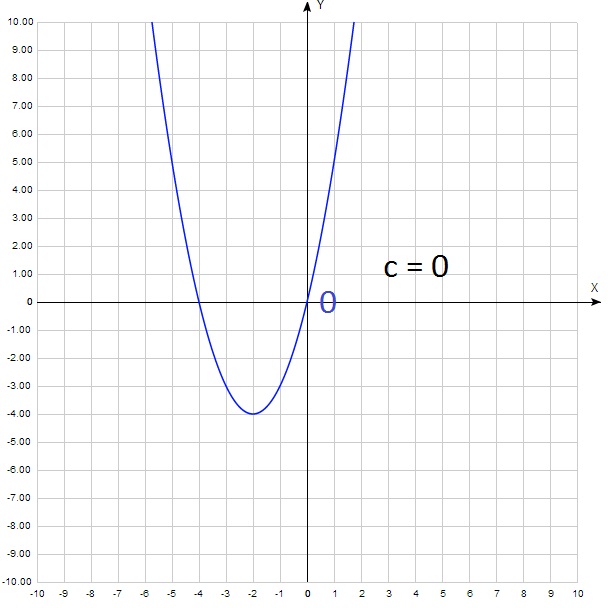
Соответственно, если с = 0, то парабола обязательно будет проходить через начало координат:
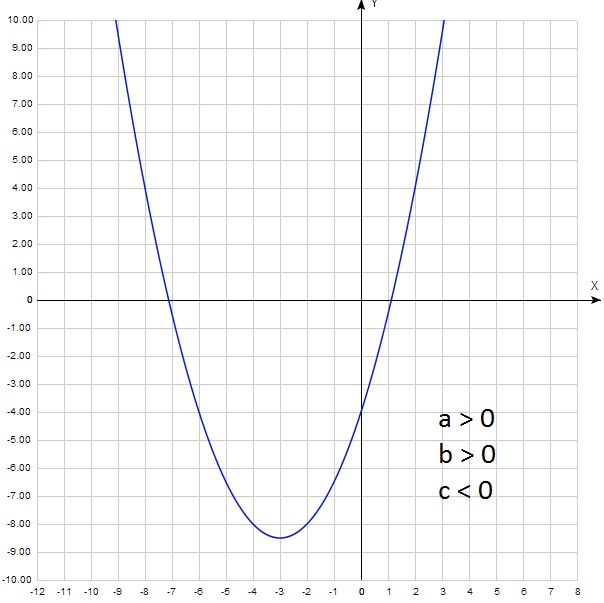
Ветви направлены вверх, значит а > 0, парабола пересекает ось у ниже нуля, значит с 0. Окончательно имеем: а > 0, b > 0, с 0)
тел. моб. (495) 642 42 50. Звонить можно до 23:00.
тел. моб. 8 (499) 723 68 84. Звонить можно до 23:00.
тел. дом. 8 (925) 642 42 50. Звонить можно до 23:00.
Парабола, график, вершина, нули.
теория по математике 📈 функции
Функция вида y=ax 2 +bx+c, где а, b, с – некоторые числа, причем, а ≠ 0 число, х – переменная, называется квадратичной функцией.
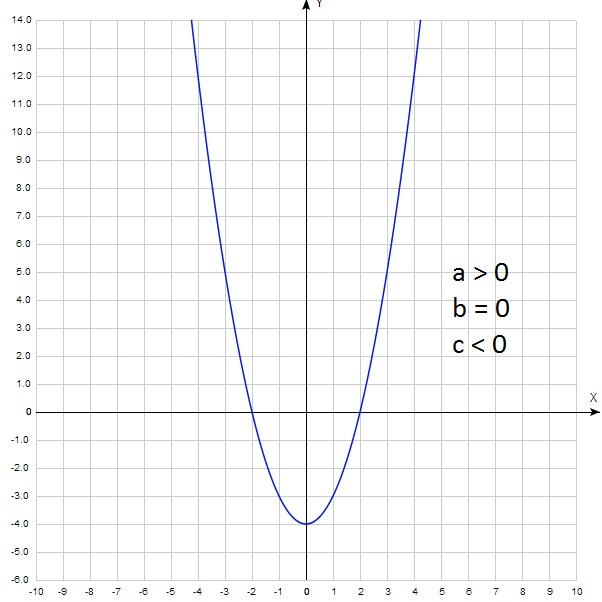
Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.
Чтобы найти координаты вершины параболы (х0; у0), надо воспользоваться формулой:
для нахождения у0 можно просто подставить значение х0 в формулу данной функции y0=ax 2 +bx+c вместо х.
Рассмотрим это на примере конкретно заданной функции.
Пример №1
Найти вершину параболы, заданной формулой у=2х 2 – 8х + 5.
Найдем, чему равны коэффициенты: а=2; b= – 8
Подставим их в формулу и вычислим значение х0:
Теперь в заданную по условию формулу вместо х подставим найденное значение у0=2 ∙ 2 2 – 8 ∙ 2 + 5=8 – 16 + 5= –3
Итак, мы нашли координаты вершины параболы: (2; –3).
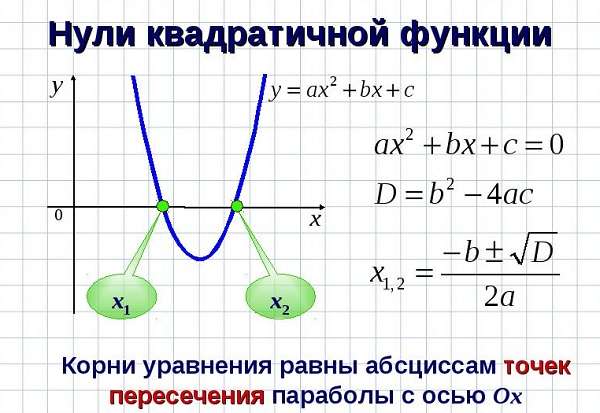
Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.
Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.
Пример №2
Найти нули функции у=х 2 +4х – 5
Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х 2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:
D=b 2 – 4ac=4 2 — 4 ∙ 1 ∙ ( − 5 ) = 36
Значит, нули функции равны –5 и 1
Примечание к заданию по нахождению нулей функции без графика
Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).
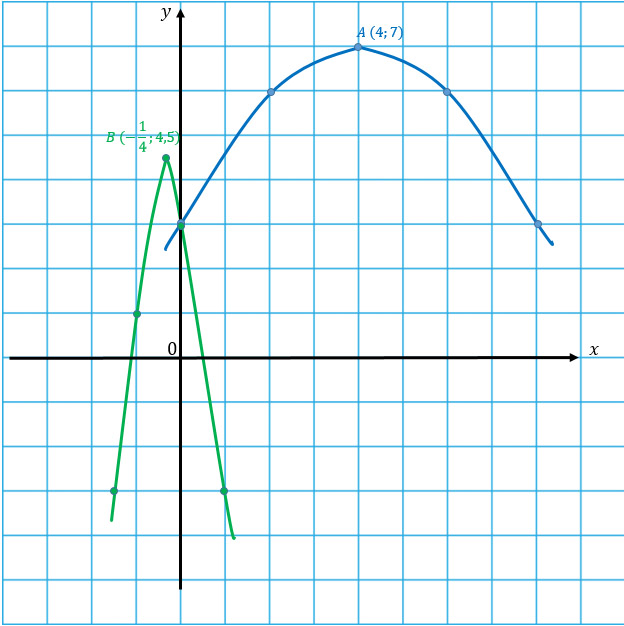
Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.
Пример №3
Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.
Теперь можно выполнить соответствие:
Пример №4
Рассмотрим еще пример на соответствие
В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х0.
Итак, найдем х0 для формулы «Б»:
Видим, что х0 отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.
А) a>0, с >0 Б) а 0 В) а>0, с
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a 0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с 0, с >0 — это график №1
Б) а 0 — это график №3
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х 2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3
pазбирался: Даниил Романович | обсудить разбор | оценить
На рисунках изображены графики функций вида
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
Из всего вышеперечисленного можно найти ответ:
pазбирался: Даниил Романович | обсудить разбор | оценить
Парабола свойства и график квадратичной функции
Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.
Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.
Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.
Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.
Что такое парабола и как она выглядит
Алгебра: под этим термином понимается график квадратичной функции.
Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:
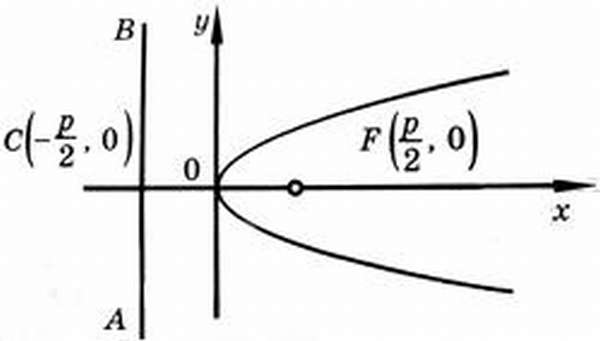
Каноническое уравнение параболы
На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.
Каноническое уравнение имеет вид:
где коэффициент p – фокальный параметр параболы (AF).
В алгебре оно запишется иначе:
y = a x2 + b x + c (узнаваемый шаблон: y = x2).
Свойства и график квадратичной функции
Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.
Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.
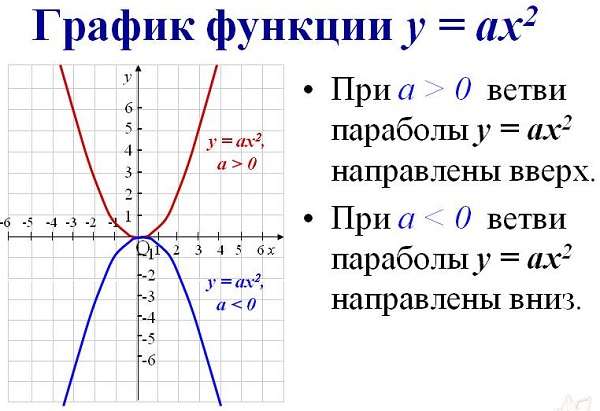
Как определить, куда направлены ветви параболы
Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.
Как найти вершину параболы по формуле
Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.
Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.
Формулы нахождения вершины:
Пример.
Имеется функция у = 4 * x2 + 16 * x – 25. Найдём вершины этой функции.
Смещение параболы
Классический случай, когда в квадратичной функции y = a x2 + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0, 0).
Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.
Пример.
Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 по оси ординат.
Как строить параболу по квадратному уравнению
Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.
Анализируя выражения и уравнения, можно увидеть следующее:
Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:
Для этого нужно приравнять выражение к нулю.
Наличие корней параболы зависит от результата:
Получаем алгоритм построения параболы:
Пример 1.
Дана функция у = х2 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:
По полученным точкам можно построить параболу.
Пример 2.
Для функции у = 3 * х2 2 * х 1 нужно построить параболу. Действуем по приведенному алгоритму:
По полученным точкам можно построить параболу.
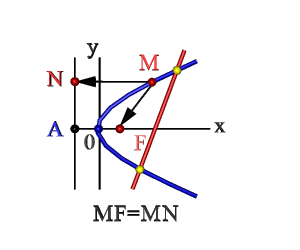
Директриса, эксцентриситет, фокус параболы
Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).
Эксцентриситет (константа) = 1.
Заключение
Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.