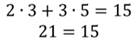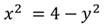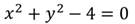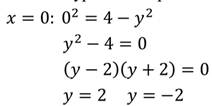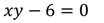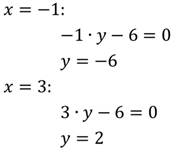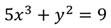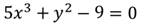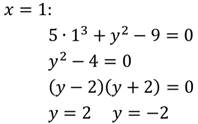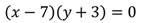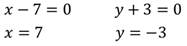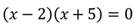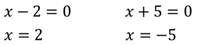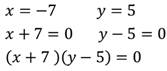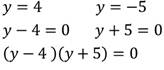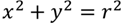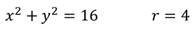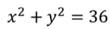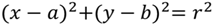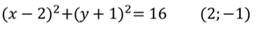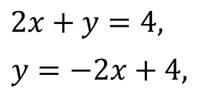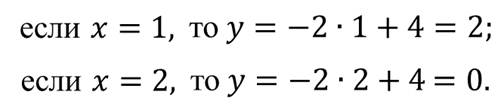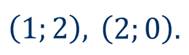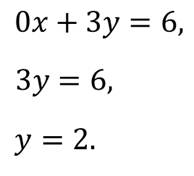Что такое график уравнения с двумя переменными

Уравнение с двумя переменными и его график

Урок 15. Алгебра 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Уравнение с двумя переменными и его график»

· уравнения с двумя переменными;

· решения уравнения с двумя переменными;

· степень уравнения с двумя переменными;

· график уравнения с двумя переменными.

Перед вами записаны уравнения:

Все они являются уравнениями с двумя переменными, так как в каждом из них есть две переменные. Возьмём, например, первое уравнение и подставим в него x=3 и y=5:

Получили неверное равенство. А если подставим x=3 и y=3, то получим верное числовое равенство.

Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное числовое равенство.

Пара чисел (3; 3) является решением данного уравнения. Но это не единственное решение.

Для определения степени уравнения с двумя переменными, нужно преобразовать его так, чтобы в левой части стоял многочлен стандартного вида, а справа ноль. Тогда степень уравнения считают равной степени данного многочлена.

Чтобы определить степень многочлена с двумя переменными, нужно определить степень каждого одночлена, входящего в состав многочлена, и выбрать из них наибольшую. Степень данного уравнения равна 1.

Определить степени уравнений и найти любых два решения.

1. Рассмотрим уравнение:

Степень данного уравнения равна 2.

Найдём два любых решения:

2. Решить уравнение:

Степень уравнения равна 2.

Найдём два решения уравнения:

3. Решить уравнение:

Степень данного уравнения равна 3.

Найдём любые два решения:

В ходе выполнения заданий стало понятно, что уравнения с двумя переменными имеют много решений. И указать все решения достаточно сложно. Если решением является пара значений, то его можно изобразить на координатной плоскости в виде точки. Так все решения и образуют график уравнения с двумя переменными.

Графиком уравнения с двумя переменными является множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.

1. Построить график уравнения:

Так как произведение равно нулю, то каждый из множителей также равен нулю. Решим каждое из полученных уравнений:

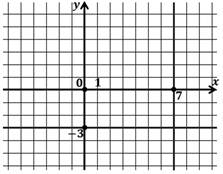
Изобразим график данного уравнения:

Решением являются две прямые: х=7 и у=-3.

2. Построить график уравнения:

Так как произведение равно нулю, то каждый из множителей также равен нулю. Решим каждое из полученных уравнений:

Изобразим график данного уравнения:

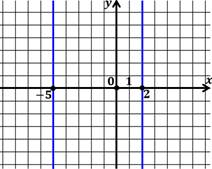
Решением являются две прямые: х=-5 и х=2.

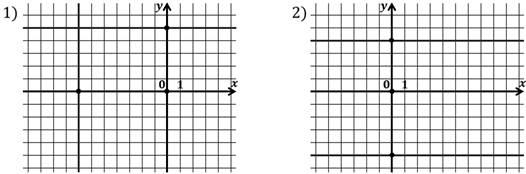
Составить уравнения, графиками которых являются пары прямых, изображённых на рисунках.

Посмотрим на первый рисунок:

Получили, что прямые являются графиком уравнения.

Обратимся ко второму случаю:

Получили, что эти прямые являются графиком уравнения.

Графиком уравнения является окружность с центром в точке начала координат и радиусом r.

Например, графиком уравнения:

является окружность с r=4.

Записать уравнение окружности с центром в точке начала координат и r=6.

Получим уравнение окружности:

Если центром окружности не является точка начала координат, то уравнение окружности будет выглядеть так:

Центр окружности имеет координаты (a; b).

Выполним обратное действие. Но для записи уравнения окружности уже не достаточно только координат центра, необходимо знать и радиус. Например:

Источник

Алгебра. 9 класс

Рассмотрим уравнение 3x 2 + y = 13.

Это уравнение является уравнением с двумя переменными x и y.

При подстановке вместо переменной x числа 2, а вместо переменной y числа 1 мы получим верное равенство.

Значит, пара чисел 2 и 1 является решением данного уравнения. Эту пару чисел записывают в круглых скобках, причём на первом месте записывают значение переменной x, а на втором – значение переменной y: (2; 1).

Итак, сформулируем определение решения уравнения с двумя переменными.

Решением уравнения с двумя переменными называется пара значений переменных, обращающая уравнение в верное равенство.

Если все эти пары чисел представить как координаты точек и изобразить на координатной плоскости, то получится график данного уравнения.

Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.

Вспомним, что является графиком линейного уравнения с двумя переменными.

Графиком этого уравнения является окружность с центром в точке с координатами (а; b) и радиусом r.

Все пары чисел, которые будут являться решением данного уравнения, при изображении их на координатной плоскости будут принадлежать окружности с центром в точке с координатами (1; 2) и радиусом, равным 3.

Источник

Тема урока: «Уравнение с двумя переменными и его график»

Разделы: Математика

ЦЕЛЬ:1) Познакомить учащихся с понятием «уравнение с двумя переменными»;

2) Научить определять степень уравнения с двумя переменными;

3) Научить определять по заданной функции, какая фигура является графиком

4) Рассмотреть преобразования графиков с двумя переменными;

5) Учить учащихся «читать» графики и выполнять построение графиков по

заданному уравнению с двумя переменными, используя программу Agrapher ;

6) Развивать логическое мышление учащихся.

(лекция проводится с использованием авторских слайдов; построение графиков выполнено в программе Agrapher)

У: При изучении линий возникают две задачи:

По геометрическим свойствам данной линии найти её уравнение;

Обратная задача: по заданному уравнению линии исследовать её геометрические свойства.

Первую задачу мы рассматривали в курсе геометрии применительно к окружности и прямой.

Сегодня мы будем рассматривать обратную задачу.

Рассмотрим уравнения вида:

– это примеры уравнений с двумя переменными.

Уравнения с двумя переменными х и у имеет вид f(x,y)= (x,y), где f и – выражения с переменными х и у.

Пара (-1; 3) значений переменных х и у является решением уравнения х(х-у)=4.

То есть решением уравнения с двумя переменными называют множество упорядоченных пар значений переменных, образующих это уравнение в верное равенство.

Уравнения с двумя переменными имеет, как правило, бесконечно много решений. Исключения составляют, например, такие уравнения, как х 2 +( у 2 — 4 ) 2 = 0 или

Уравнение х 4 + у 4 +3 = 0 вообще не имеет решений. Представляет интерес, когда значениями переменных в уравнении служат целые числа. Решая такие уравнения с двумя переменными, находят пары целых чисел. В таких случаях говорят, что уравнения решено в целых числах.

Степенью уравнения с двумя переменными, представленного в виде F(х, у) = 0, где F(х,у)-многочлен стандартного вида, называют степень многочлена F(х, у).

Если все решения уравнения с двумя переменными изобразить точками в координатной плоскости, то получится график уравнения с двумя переменными.

Графиком уравнения с двумя переменными называется множество точек, координаты которых служат решениями этого уравнения.

Так, график уравнения ax + by + c = 0 представляет собой прямую, если хотя бы один из коэффициентов a или b не равен нулю(рис.1). Если a = b = c = 0, то графиком этого уравнения является координатная плоскость(рис.2), если же a = b = 0, а c0, то графиком является пустое множество(рис.3).

График уравнения y = a х 2 + by + c представляет собой параболу(рис.4), график уравнения xy=k (k0 ) – гиперболу(рис.5). Графиком уравнения х 2 + у 2 = r, где x и y – переменные, r – положительное число, является окружность с центром в начале координат и радиусом равным r(рис.6). Графиком уравнения является эллипс, где a и b – большая и малая полуоси эллипса (рис.7).

Построение графиков некоторых уравнений облегчается использованием их преобразований. Рассмотрим преобразования графиков уравнений с двумя переменными и сформулируем правила, по которым выполняются простейшие преобразования графиков уравнений

1) График уравнения F (-x, y) = 0 получается из графика уравнения F (x, y) = 0 с помощью симметрии относительно оси у.

9) График уравнения F (x, y) = 0 в результате поворота около начала координат на угол 45 0 по часовой стрелке переходит в график уравнения F = 0, а против часовой стрелки – в график уравнения F = 0.

Из рассмотренных нами правил преобразования графиков уравнений с двумя переменными легко получаются правила преобразования графиков функций.

Пример 1. Покажем, что графиком уравнения х 2 + у 2 + 2х – 8у + 8 = 0 является окружность (рис.17).

Преобразуем уравнение следующим образом:

3) проанализируем, согласно правилам преобразования графиков уравнений с двумя переменными, уравнение (х + 1) 2 + (у – 4) 2 = 3 2 : графиком данного уравнения является окружность с центром в точке (-1; 4) и радиусом 3 единицы.

Пример 2. Построим график уравнения х 2 + 4у 2 = 9.

Начертим окружность с центром в начале координат и радиусом 3 единицы.

Уменьшим в 2 раза расстояние каждой её точки от оси Х, получим график уравнения

Мы получили фигуру с помощью сжатия окружности к одному из её диаметров(к диаметру, который лежит на на оси Х). Такую фигуру называют эллипсом (рис.18).

Воспользуемся формулой F= 0.

Подставим в данное уравнение вместо Х и вместо У, получим:

У: Что представляет собой график уравнения у = ?

Д: Графиком уравнения у = является гипербола.

Какая линия будет являться графиком данного уравнения?

У: Какие прямые являются асимптотами гиперболы у = .

Д: Асимптотами гиперболы у = являются прямые у = 0 и х = 0.

Пример 4 : Выясним, какой вид примет уравнение у = х 2 параболы при повороте около начала координат на угол 90 0 по часовой стрелке.

(учащимся выдаются «Карточки-инструкции» по выполнению построений графиков уравнений с двумя переменными в программе Agrapher (Приложение 2) и карточки «Практическое задание» (Приложение 3) с формулировкой заданий 1-8 Графики уравнений к заданиям 4-5 учитель демонстрирует на слайдах).

Ответ:

Решение: 1)Подставим вместо Х в заданное уравнение значение 3.

2)Получим квадратное уравнение относительно переменной У, имеющее вид:

4) Решим это уравнение:

Задание3. Определите степень уравнения:

Ответ: а) 3; б) 5; в) 4; г) 4.

Задание4. Какая фигура является графиком уравнения:

Ответ: а) прямая (рис.23а); б) парабола, ветви которой направлены вверх (рис.23б); в) парабола, ветви которой направлены вверх (рис.23в), г) две параллельные прямые х = 1,5 и х = 4 (рис.23г); д) гипербола (рис.23д); е) окружность, с центром в начале координат, радиусом равным 3 (рис.23е).

Проверьте с помощью программы Agrapher правильность выполнения задания.

а) от оси х в 2 раза; б) от оси у в 3 раза.

Проверьте с помощью программы Agrapher правильность выполнения задания.

Задание7. На рисунке (рис.29) изображен график уравнения с двумя переменными. Найдите по графику (приближенно) два решения:

б) с противоположными значениями у: у = 1, 2

Задание8. Сравните взаимное расположение данных прямых и определите, каким преобразованием плоскости график первой прямой переводится в график второй прямой.

а) 3х-7у = 5 и 3(х-1)-7у = 5

б) 3х-7у = 5 и 3(х-1)-7(у+3) =5

в) 3х-7у = 5 и 3х + 7у = 5

е) 3х-7у = 5 и 7х-3у = 5

Ответ: а) прямые параллельны, перемещение параллельно оси х на 1 единицу вправо (рис.26а);

б) прямые параллельны, перемещение параллельно оси х на 1 единицу вправо и параллельно оси у на 3 единицы вниз (рис.26б);

в) прямые пересекаются, симметричное отображение относительно оси х (рис.26в);

г) прямые пересекаются, симметричное отображение относительно оси у (рис.26г);

д) прямые параллельны, симметричное отображение относительно начала координат (рис.26д);

е) прямые пересекаются, поворот около начала координат на 90по часовой стрелке и симметричное отображение относительно оси х (рис.26е).

III. Самостоятельная работа обучающего характера.

(учащимся выдаются карточки «Самостоятельная работа» и «Отчётная таблица результатов самостоятельной работы», в которую учащиеся записывают свои ответы и после самопроверки, по предложенной схеме оценивают работу) Приложение 4..

1.Определите степень уравнения:

2. Является ли пара чисел (-2;3) решением уравнения:

3. Найдите множество решений уравнения:

4. Какой кривой (гиперболой, окружностью, параболой) является множество точек, если уравнение этой кривой имеет вид:

(проверьте с помощью программы Agrapher правильность выполнения задания)

5. Постройте, используя программуAgrapher, график уравнения:

Укажите координаты центра окружности и её радиус.

Проверьте свой ответ, выполнив графическое построение, используя программу Agrapher.

1.Определите степень уравнения:

2. Является ли пара чисел (-2;3) решением уравнения:

3. Найдите множество решений уравнения:

4. Какой кривой (гиперболой, окружностью, параболой) является множество точек, если уравнение этой кривой имеет вид:

(проверьте с помощью программы Agrapher правильность выполнения задания)

5. Постройте, используя программуAgrapher, график уравнения:

Источник

График линейного уравнения с двумя переменными

Урок 40. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «График линейного уравнения с двумя переменными»

· ввести понятие «график линейного уравнения с двумя переменными»;

· рассмотреть поведение графика в зависимости от значений коэффициентов перед переменными.

На прошлом уроке мы с вами познакомились с линейным уравнением с двумя переменным. Давайте, вспомним определение.

И сегодня на уроке мы будем вести речь о графике такого уравнения.

Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями этого уравнения.

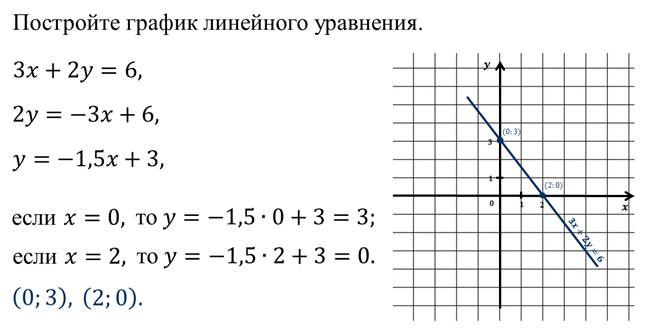
Обратите внимание, что полученная формула имеет вид линейной функции, графиком которой является прямая.

Так как прямая определяется двумя точками, то для построения графика нам достаточно указать две точки. Так:

Таким образом, получили две точки с координатами:

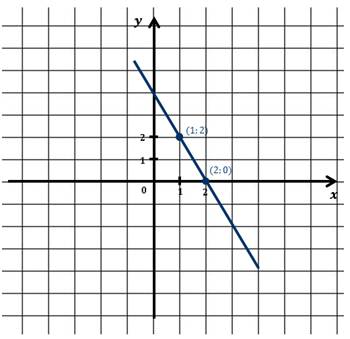
Теперь на координатной плоскости отметим эти точки и проведём через них линию.

Эта прямая является графиком исходного уравнения.

Все точки, принадлежащие графику, – это пары чисел, которые являются решениями нашего уравнения.

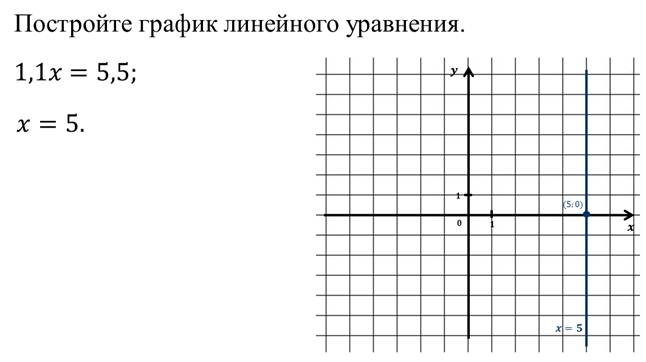
Теперь рассмотрим уравнение, в котором коэффициент при одной из переменных равен нулю.

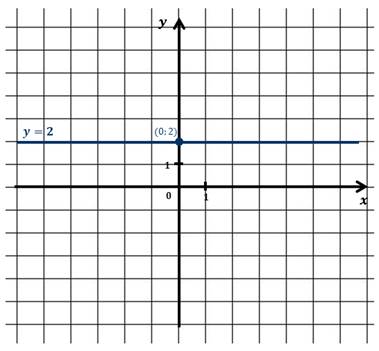
А это постоянная функция. С предыдущих уроков нам известно, что график такой функции – это прямая, которая проходит через точку с координатами (0; 2) и параллельна оси Ox.

Все точки, принадлежащие этой прямой, – это пары чисел, которые являются решениями данного уравнения. И таких решений бесконечно много.

Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.

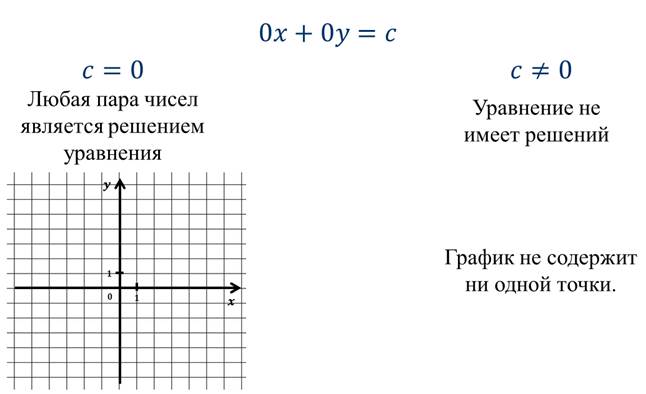
А теперь давайте рассмотрим случай, когда в линейном уравнении оба коэффициента при переменных равны нулю.

Давайте, рассмотрим примеры построения графиков линейных уравнений.

Итак, сегодня на уроке мы выяснили, что же представляет собой график линейного уравнения с двумя переменными и научились строить такие графики.

Источник