Что такое график зависимости

Урок 48 Бесплатно Графики

Человеком накоплено огромное множество разнообразной информации.

Различают информацию по доступности, по целям использования, по принадлежности к определённой области науки. Информация может быть истиной и ложной, динамической и статической, аналоговой и дискретной и др.

С полученной информацией человек совершает различные действия: передает, запоминает, записывает, сохраняет, преобразует и т.д.

Информация может быть представлена и передана разными способами: в виде текста (совокупности алфавитных, цифровых, специальных символов и знаков), в виде звуков и с помощью видеосигналов, а также графическим способом (схемы, рисунки, диаграммы, чертежи, таблицы, графики).

Узнаем, что представляют собой графики, определим область их применения.

Научимся читать графики и строить их по заданным значениям.

График и его основные элементы

В современном мире объем информации и научных знаний, которые получает человек, огромен.

Становится все труднее воспринимать и обрабатывать большие потоки информации, так чтобы информация оставалась точной, надежной, понятной и достоверной.

Важно уметь верно выбрать средства и способы передачи, обработки и представления информации.

Как известно, одну и туже информацию можно представить несколькими способами.

Например, дерево можно описать словом в текстовом виде, словом в звуковом варианте или с помощью графического изображения.

Особенно полно и точно представить информацию возможно в виде текста, но чаще всего такой способ представления информации очень объемный, что затрудняет восприятие и усвоение.

Графическое же изображение позволяет нам кратко, качественно и наглядно представить информацию.

С помощью различных видов графического способа представления информации легко устанавливать логические и причинно-следственные связи и отношения.

Необходимо уметь находить и выбирать наиболее выгодный способ обработки и представления информации.

Например, удобно и просто представлять информацию с помощью таблиц, но в тоже время восприятие громоздких и объемных таблиц уже оказывается затруднительным.

Таблица, содержащая большое количество столбцов и строк, даже если информация была подобрана достоверно и качественно, теряет наглядность и привлекательность.

Большой объем информации удобно представлять в виде диаграмм и графиков.

Уроком ранее вы уже познакомились с диаграммами и знаете, что это графический способ представления информации, изображение соотношения и зависимостей между величинами при помощи фигур, площади и размер которых пропорциональны исследуемым величинам.

Преимущества диаграмм, по сравнению с таблицами или текстовой информацией, заключается в наглядности, в возможности сравнивать и анализировать исследуемые величины друг с другом, компактно представлять большой объем информации.

Однако получить информацию с помощью таблицы и диаграммы можно только ту, которая была определена или измерена.

Родители мальчика каждый год с рождения до 7 лет измеряли его рост и заносили данные в таблицу.

Диаграмма изменения роста мальчика будет выглядеть так:

По таблице и диаграмме невозможно определить промежуточные значения.

Трудно определить рост мальчика, например, когда ему было 4 года 3 месяца.

Заносились показания роста один раз в начале каждого года. Понятно, что у мальчика рост менялся не скачками, а с течением времени плавно.

Непрерывность происходящего и исследуемого процесса можно изобразить с помощью графиков.

Такой вид графического изображения также имеет большое иллюстративное значение, доходчиво и понятно позволяет показать динамику изменения данных с течением времени или по упорядоченным категориям данных.

В Большом энциклопедическом словаре дается такое определение графика:

Чтобы построить график, необходимо изобразить координатную плоскость с прямоугольной системой координат.

Значение независимых величин обычно откладывают на горизонтальной оси (оси Ох— оси абсцисс).

Значение зависимых величин обычно откладывают на вертикальной оси (оси Оу— оси ординат).

Положительные значения величин откладываются обычно вправо и вверх от точки начала отсчета.

При изменении независимой величины зависимая величина меняется каким-либо образом.

Пройденный путь (зависимая величина) зависит от времени (независимая величина).

Таким образом, график показывает, как изменяется значение ординаты при изменении значений абсциссы.

На координатной оси графика наносятся шкалы, характеризующие числовое значение используемых величин.

Интервалы шкалы определяют масштаб графиков по координатным осям.

Цифровые значения располагают под горизонтальной шкалой и левее вертикальной.

Масштаб влияет на точность графика, он должен быть простым и понятным.

Размер графика должен соответствовать назначению.

Чем объемней и сложнее график, тем больше его размеры должны быть.

В сложных больших графиках изображают координатную сетку: горизонтальные и вертикальные линии, проведенные через каждое деление шкалы.

Зависимость величин изображается в виде линии, точек (меток) или в виде точек (меток) и линии.

Линию графика зависимости величин (это может быть прямая, кривая, ломаная) называют линией графического образа.

Точки на графике могут иметь различную форму и размер.

Проводить графический образ нужно как можно ближе к полученным точкам.

Если на графике изображают несколько различных зависимостей, то дается пояснение каждой линии вне поля графика.

Сами линии графического образа принято изображать линиями разного начертания или разного цвета.

Графики удобно изображать на миллиметровой бумаге для большей наглядности.

Примерный алгоритм построения графика.

Вернемся к таблице изменения роста мальчика, которую мы рассмотрели ранее.

Источник

Что такое график зависимости

Графическое представление равномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

Проекция перемещения тела численно равна площади прямоугольника АОВС под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.

Из графика видно, что проекция скорости равна:

Рассмотрев эту формулу, мы можем сказать, чем больше угол, тем быстрей движется тело и оно проходит больший путь за меньшее время.

Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.

Неравномерное прямолинейное движение.

Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.

Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным или переменным движением.

Для характеристики неравномерного движения вводится понятие средней скорости.

Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.

В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:

Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.

Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.

Различие между средней и мгновенной скоростями показано на рисунке.

Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.

Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:

V_x — Скорость тела при равноускоренном движении по прямой

V_x o — Начальная скорость тела

a_x — Ускорение тела

t — Время движения тела

Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.

Единица измерения ускорения в СИ [м/с 2 ].

Ускорение измеряют акселерометром

Уравнение скорости для равноускоренного движения: v_x = v_xo + a_xt

Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):

S_x — Перемещение тела при равноускоренном движении по прямой

V_x o — Начальная скорость тела

V_x — Скорость тела при равноускоренном движении по прямой

a_x — Ускорение тела

t — Время движения тела

Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:

— если известны начальная, конечная скорости движения и ускорение.

— если известны начальная, конечная скорости движения и время всего движения

Графическое представление неравномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости:

В координатах зависимость имеет вид:

Источник

График зависимости пути от времени

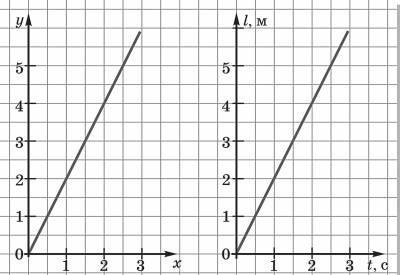
Во многих случаях движение тел удобно описывать с помощью графиков. Такой способ описания движения достаточно нагляден. В курсе математики уже изучались графики некоторых функций. Проанализируем графики движения и скорости: l = f (t) и v = f (t). Вспомним, как на уроках математики графически выражали зависимость одной величины от изменения другой. Для расчета пройденного с постоянной скоростью пути мы используем формулу l = vt. На уроках математики мы использовали уравнения y = kx.

График движения дает такое же полное описание движения, как и формула l = vt.

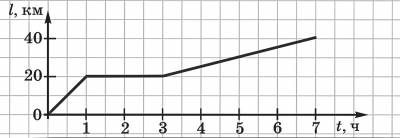
Например, пусть нам известен график равномерного движения тела.

С помощью этого графика мы можем получить определенные сведения о движении тела. За 1 час тело проехало 20 км, затем 2 часа тело стояло, а потом за 4 часа тело проехало еще 20 км. При этом по графику мы можем определить и скорость движения:

v 1 =20 км/час, v 2 =0, v 3 = 5 км/час.

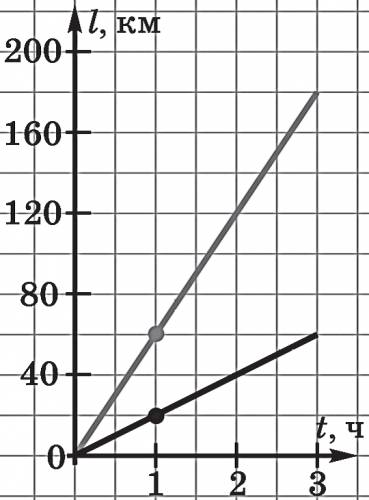
Рассмотрим теперь, чем отличаются графики зависимости пути от времени для тел, движущихся с различной скоростью.

Стоит обратить внимание учащихся на такой очень важный факт: чем больше скорость тела, тем больше угол между графиком зависимости пути от времени и осью времени. 2. Графики зависимости скорости от времени Наряду с графиками движения часто пользуются графиками скорости. Для построения графика скорости применяют прямоугольную систему координат, по горизонтальной оси которой откладывают в определенном масштабе времени, а по вертикальной — модуль скорости.

С этого графика можно определить, что скорость первого тела 25 м/с, а второго — 10 м/с.

Проверьте себя

1. Какой вид имеет график зависимости пути от времени при прямолинейном равномерном движении?

2. Чем отличаются графики зависимости пути от времени для двух тел, движущихся с различной скоростью?

3. Как по графику пути для двух тел сравнить скорости их движения?

4. Как по графику скорости определить пройденный телом путь?

Закрепление изученного материала

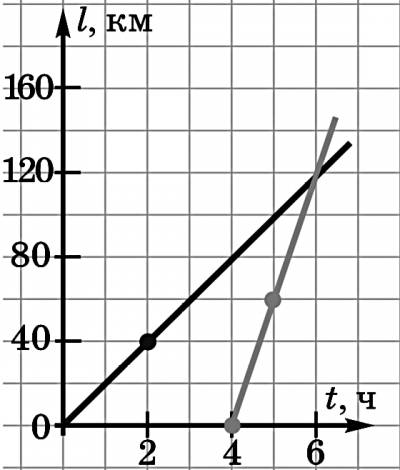
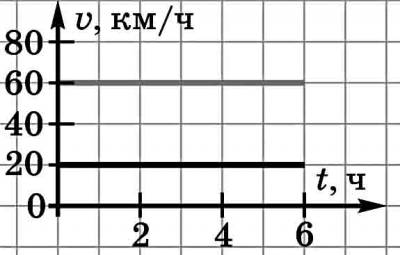
Из поселка выехал велосипедист со скоростью 20 км / ч, а через 4 часа после него — автомобиль со скоростью 60 км / ч. Через сколько часов после своего выезда автомобиль догонит велосипедиста? Решите задачу графически.

Решение. Графики пересекаются при t = 6 ч, считая с момента выезда велосипедиста, то есть через 2 часа после выезда автомобиля.

2. По графику определите скорость движения каждого тела. Какой путь прошли оба тела с 3 с? Постройте графики пути.

3. На рисунке приведены графики зависимости пути от времени для двух автомобилей. Скорость которого из автомобилей больше? Почему вы так считаете?

Источник

Что такое график зависимости

3.1. Равнопеременное движение по прямой.

3.1.1. Равнопеременное движение по прямой — движение по прямой с постоянным по модулю и направлению ускорением:

3.1.2. Ускорение () — физическая векторная величина, показывающая, на сколько изменится скорость за 1 с.

где — начальная скорость тела, — скорость тела в момент времени t.

В проекции на ось Ox:

где — проекция начальной скорости на ось Ox, — проекция скорости тела на ось Ox в момент времени t.

Знаки проекций зависят от направления векторов и оси Ox.

3.1.3. График проекции ускорения от времени.

При равнопеременном движении ускорение постоянно, поэтому будет представлять собой прямые линии, параллельные оси времени (см. рис.):

Значение ускорения: чем дальше от оси времени лежит прямая, тем больше модуль ускорения

3.1.4. Скорость при равнопеременном движении.

В проекции на ось Ox:

Для равноускоренного движения:

Для равнозамедленного движения:

3.1.5. График проекции скорости в зависимости от времени.

График проекции скорости от времени — прямая линия.

Направление движения: если график (или часть его) находятся над осью времени, то тело движется в положительном направлении оси Ox.

Значение ускорения: чем больше тангенс угла наклона (чем круче поднимается вверх или опускает вниз), тем больше модуль ускорения; где — изменение скорости за время

Пересечение с осью времени: если график пересекает ось времени, то до точки пересечения тело тормозило (равнозамедленное движение), а после точки пересечения начало разгоняться в противоположную сторону (равноускоренное движение).

3.1.6. Геометрический смысл площади под графиком в осях

Площадь под графиком, когда на оси Oy отложена скорость, а на оси Ox — время — это путь, пройденный телом.

На рис. 3.5 нарисован случай равноускоренного движения. Путь в данном случае будет равен площади трапеции:

(3.9)

3.1.7. Формулы для расчета пути

(3.10)

(3.12)

(3.11)

(3.13)

(3.14)

Все формулы, представленные в таблице, работают только при сохранении направления движения, то есть до пересечения прямой с осью времени на графике зависимости проекции скорости от времени.

Если же пересечение произошло, то движение проще разбить на два этапа:

до пересечения (торможение):

После пересечения (разгон, движение в обратную сторону)

В формулах выше — время от начала движения до пересечения с осью времени (время до остановки), — путь, который прошло тело от начала движения до пересечения с осью времени, — время, прошедшее с момента пересечения оси времени до данного момента t, — путь, который прошло тело в обратном направлении за время, прошедшее с момента пересечения оси времени до данного момента t, — модуль вектора перемещения за все время движения, L — путь, пройденный телом за все время движения.

За время тело пройдет путь:

За время тело пройдет путь:

За промежуток можно принимать любой отрезок времени. Чаще всего с.

Если то

Тогда за 1-ую секунду тело проходит путь:

Если внимательно посмотрим, то увидим, что и т. д.

Таким образом, приходим к формуле:

Словами: пути, проходимые телом за последовательные промежутки времени соотносятся между собой как ряд нечетных чисел, и это не зависит от того, с каким ускорением движется тело. Подчеркнем, что это соотношение справедливо при

3.1.9. Уравнение координаты тела при равнопеременном движении

Знаки проекций начальной скорости и ускорения зависят от взаимного расположения соответствующих векторов и оси Ox.

Для решения задач к уравнению необходимо добавлять уравнение изменения проекции скорости на ось:

3.2. Графики кинематических величин при прямолинейном движении

3.3. Свободное падение тела

Под свободным падением подразумевается следующая физическая модель:

1) Падение происходит под действием силы тяжести:

2) Сопротивление воздуха отсутствует (в задачах иногда пишут «сопротивлением воздуха пренебречь»);

3) Все тела, независимо от массы падают с одинаковым ускорением (иногда добавляют — «независимо от формы тела», но мы рассматриваем движение только материальной точки, поэтому форма тела уже не учитывается);

4) Ускорение свободного падения направлено строго вниз и на поверхности Земли равно (в задачах часто принимаем для удобства подсчетов);

3.3.1. Уравнения движения в проекции на ось Oy

В отличии от движения по горизонтальной прямой, когда далеко не всех задач происходит смена направления движения, при свободном падении лучше всего сразу пользоваться уравнениями, записанными в проекциях на ось Oy.

Уравнение координаты тела:

Уравнение проекции скорости:

Как правило, в задачах удобно выбрать ось Oy следующим образом:

Ось Oy направлена вертикально вверх;

Начало координат совпадает с уровнем Земли или самой нижней точкой траектории.

При таком выборе уравнения и перепишутся в следующем виде:

3.4. Движение в плоскости Oxy.

Мы рассмотрели движение тела с ускорением вдоль прямой. Однако этим равнопеременное движение не ограничивается. Например, тело, брошенное под углом к горизонту. В таких задачах необходимо учитывать движение сразу по двум осям:

Или в векторном виде:

И изменение проекции скорости на обе оси:

3.5. Применение понятия производной и интеграла

Мы не будем приводить здесь подробное определение производной и интеграла. Для решения задач нам понадобятся лишь небольшой набор формул.

где A, B и то есть постоянные величины.

Теперь посмотрим, как понятие производной и интеграла применимо к физическим величинам. В математике производная обозначается «’», в физике производная по времени обозначается «∙» над функцией.

то есть скорость является производной от радиус-вектора.

Для проекции скорости:

то есть ускорение является производной от скорости.

Для проекции ускорения:

Таким образом, если известен закон движения то легко можем найти и скорость и ускорение тела.

Теперь воспользуемся понятием интеграла.

то есть, скорость можно найти как интеграл по времени от ускорения.

то есть, радиус-вектор можно найти, взяв интеграл от функции скорости.

Таким образом, если известна функция то легко можем найти и скорость, и закон движения тела.

Константы в формулах определяются из начальных условий — значения и в момент времени

3.6. Треугольник скоростей и треугольник перемещений

3.6.1. Треугольник скоростей

В векторном виде при постоянном ускорении закон изменения скорости имеет вид (3.5):

Эта формула означает, что вектор равен векторной сумме векторов и Векторную сумму всегда можно изобразить на рисунке (см. рис.).

В каждой задаче, в зависимости от условий, треугольник скоростей будет иметь свой вид. Такое представление позволяет использовать при решении геометрические соображения, что часто упрощает решение задачи.

3.6.2. Треугольник перемещений

В векторном виде закон движения при постоянном ускорении имеет вид:

При решении задачи можно выбирать систему отсчета наиболее удобным образом, поэтому не теряя общности, можем выбрать систему отсчета так, что то есть начало системы координат помещаем в точку, где в начальный момент находится тело. Тогда

то есть вектор равен векторной сумме векторов и Изобразим на рисунке (см. рис.).

Как и в предыдущем случае в зависимости от условий треугольник перемещений будет иметь свой вид. Такое представление позволяет использовать при решении геометрические соображения, что часто упрощает решение задачи.

Источник