Что такое наибольшее двузначное число
Числа от 1 до 100. Состав числа. Круглые числа
Числа от 1 до 100
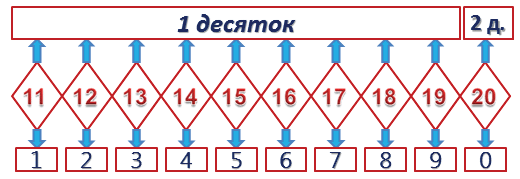
Предыдущее и последующее число
56 , 57
56, 57
Однозначные и двузначные числа
Вспомни, что каждая цифра в записи занимает определенное место.
Единицы стоят на первом месте справа.
Десятки стоят на втором месте справа.
Однозначные числа записываются ОДНОЙ цифрой: 5, 9, 2, 5.
Двузначные числа записываются ДВУМЯ цифрами: 54, 91, 42, 85.
Состав двузначного числа
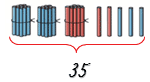
Всего на рисунке 35 палочкек.
35 = 30 + 5
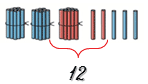
Красных палочек 12.
12 = 10 + 2
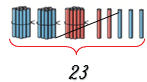
Синих палочек всего 23.
23 = 2 дес. 3 ед.
23 = 20 + 3
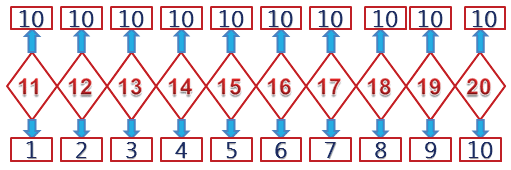
Теперь научимся представлять числа в виде суммы разрядных слагаемых.
Какие разряды выделяют в двузначных числах?
В двузначных числах выделяют разряд десятков и разряд единиц, то есть двузначное число можно представить следующим образом:
В числе 35 три десятка и 9 единиц:
Сравнение двузначных чисел
| Число | 42 | 24 |
| Количество десятков | 4 | 2 |
| Количество единиц | 2 | 4 |
1. Сравнение двузначных чисел всегда начинается с десятков.
2. Если количество десятков одинаково, тогда переходят к сравнению единиц.
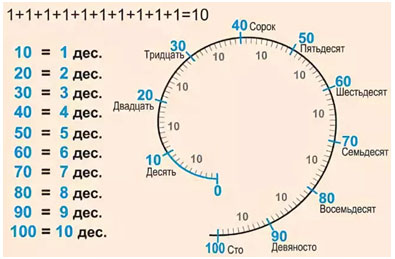
Круглые числа
10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
1 дес. + 4 дес. = 5 дес.
10 + 40 = 50
Счёт десятками
Десять любых предметов можно назвать – ОДИН ДЕСЯТОК.
Десятками можно считать:
Действия с десятками и единицами
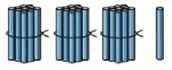
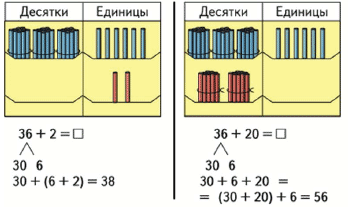
Как решить пример 34 + 25?
3 дес. и 4 ед. + 2 дес. и 5 ед. = 5 дес. 9 ед.
Можно записать короче:
Число 34 представляю в виде суммы разрядных слагаемых: 30 и 4, число 25 тоже представляю как 20 и 5. Теперь начинаю вычислять:
Сначала складываю единицы:
Теперь складываю десятки:
Запись решения выглядит так:
34 + 25 = (30 + 20) + (4 + 5) = 50 + 9 = 59
Десятки складываются с десятками.
Единицы складываются с единицами.
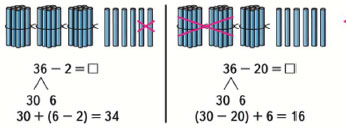
Можно рассуждать так:
Число 38 представим в виде суммы разрядных слагаемых 30 и 8, а число 16 представим так: 10 и 6. Удобно число 6 вычесть из числа 8, получим 2. Затем число 10 вычтем из числа 30, получим 20. Теперь 2 прибавим к числу 20. Получим 22.
Десятки вычитаются из десятков.
Единицы вычитаются из единиц.
Мы рассмотрели случаи устных вычислений с двузначными числами.
Познакомиться с письменными приема вычислений (сложением в столбик и вычитанием в столбик) можно в нашем справочнике.
Поделись с друзьями в социальных сетях:
Натуральные числа
Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и т. д.
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
Какие операции возможны над натуральными числами
Записывайтесь на курсы обучения математике для учеников с 1 по 11 классы!
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это примеры неправильной записи натуральных чисел, потому что ноль расположен слева. Число не может начинаться с нуля. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двузначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа самого на себя | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 × 8) |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами:
Какое самое большое двузначное число?
Вопрос конечно примитивный но..
Если смотреть с общепринятой, математической точки зрения то 99.
Потому что 9+9=18, а в сою очередь1+8=9, что выше девятки?
Но если посмотреть на двузначные числа с точки зрения
суфизма и др. то в этих областях есть свои особенный числа, с особыми значениями, выше которых только звезды, да и те подчиняются законам цифр и чисел.
Самым большим двузначным числом будет являться число состоящие из двух цифр девять и девять. Число записывается так 99 и читается девяноста девять. Слово девяноста пишется в им.п и вин.п. Д девяносто, а в остальных девяноста.
По своему значению больше, чем число «99» в арифметике не бывает. Ведь девятка самая большая цифра изо всех, поэтому число, составленное из двух девяток всегда больше любого двузначного числа. Добавишь хотя бы единичку к 99, уже получится трёхзначное число.
Девяноста девять тысяч девятьсот девяноста девять (99999)- если вопрос без подвоха. Ничего другого на ум не приходит (насколько я помню школьный курс математики, да и вообще рассуждая здраво, не претендуя на гениальность).
Это числа 1002 и 9999
наименьшее четырехзначное число равно 1000 чтобы число было кратным 3 сумма цифр этого числа должна делиться на 3 без остатка добавляем 2 получаем число 1002
наименьшее четырехзначное число кратное 3 равно 1002
наибольшее четырехзначное число равно 9999 это число кратно 3
Вряд ли существует такая статистика. Ответ, который активно минусуется пользователями проекта «Большой вопрос», скорее всего, действительно, нарушает Правила БВ. Пользователи у нас не зловредные, зря минусы не ставят, тем более, что сейчас каждый минус нужно обосновывать. Поэтому массово минусы ставятся за рекламу в ответах, за непристойности или оскорбления участников проекта или политических деятелей, за переход на личности и так далее. И в этом большинство участников «Большого вопроса» солидарны.
А слишком нехорошие ответы с большим количеством минусов модераторами удаляются, поэтому мы не можем сказать, сколько таких ответов было и сколько минусов имел самый отрицательный ответ.
Конечно, в деревне! Там что ни мужчина, тот брутал! А в городе кто? скоро одни метросексуалы будут с маникюром ))
Для этого не надо ни каких рисунков. Взрослые и так поймут, по описанию. Тут многое зависит от строения именно женского тела. Но можно рассматривать и усредненный вариант. Таких поз как минимум три, а остальные можно называть их вариантами.
Вот и все, собственно. Даже ничего рисовать не нужно.
Разряды и классы чисел
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Числа и цифры
Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.
Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.
Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определенное место — позицию.
Классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.
Названия классов многозначных чисел справа налево:
Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
А теперь прочитаем число единиц каждого класса слева направо:
Разряды чисел
От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.
Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще чтобы визуально разделить классы чисел.
Разрядные единицы обозначают так:
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Чтобы легче понимать математику — записывайтесь на наши курсы по математике!
Потренируемся
Пример 1. Записать цифрами число, в котором содержится:
Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.
Пример 2. Сколько сотен содержится в числе 6284?
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.
Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.
Значит, в данном числе содержится 62 сотни.
Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.
Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.
Напиши самое большое четное двузначное число?
Напиши самое большое четное двузначное число.
так как 99 на 2 не делится!
Значит пример решён верно!
На сколько самое большое двузначное число меньше самого маленького трехзначного числа?
На сколько самое большое двузначное число меньше самого маленького трехзначного числа.
На сколько самое маленькое двузначное число меньше самого большого трехзначного?
На сколько самое маленькое двузначное число меньше самого большого трехзначного?
Самое большое двузначное число уменьшили на самое маленькое двузначное число?
Самое большое двузначное число уменьшили на самое маленькое двузначное число.
Самое большое двузначное число кратное 7?
Самое большое двузначное число кратное 7.
Напиши самое большое двузначное число, составленное из разных нечетных цифр?
Напиши самое большое двузначное число, составленное из разных нечетных цифр.
Напиши самое маленькое двузначное число, составленное из разных четных цифр.
Самое большое четное двузначное число?
Самое большое четное двузначное число.
Напиши самое большое двузначное число, составленное из разных нечетных цифр?
Напиши самое большое двузначное число, составленное из разных нечетных цифр.
Напиши самоемаленькое двузначное число, составленное из разных четных цифр.
Сравни самое маленькое двузначное число с самым большим однозначным?
Сравни самое маленькое двузначное число с самым большим однозначным.
Самое большое чётное двузначное число?
Самое большое чётное двузначное число.
36 : 9 * 2 = 8 см ширина (36 + 8) * 2 = 94 см периметр 36 * 8 = 288 кв см площадь.
Это же 4 класс! Надо просто дробить на квадраты и треугольники, а потом складывать их площади. Как то так : Надеюсь правильно. Но точно я не знаю. ).
7, 8, 30, 9, 10, 38, 11, 12.
45 + 2 + 2 = 49 38 + 2 + 2 = 42 (49 + 42) * 2 = 182.