Что такое наибольший элемент множества
Частичный порядок
В математике частично упорядоченным множеством называется множество, на котором определено отношение частичного порядка. Неформально можно сказать, что это отношение вводит некую иерархию элементов множества, выстраивает зависимости между ними, показывает, какой элемент множества «больше», а какой «меньше». При этом такое отношение вовсе не обязано быть отношением линейного порядка, т.е. не все элементы «сравнимы».
Содержание
Формальное определение
Пары элементов, для которых не выполняется ни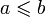 
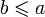
, ни 
, называются несравнимыми. В линейно упорядоченных множествах таких пар нет.
Примеры
Минимальный и наименьший элементы множества
В отличие от линейно упорядоченных множеств, для частично упорядоченных множеств различают понятия минимального и наименьшего элементов. Наименьшим элементом множества называется элемент, меньший всех остальных элементов. Минимальным элементом называется элемент, меньше которого во множестве нет. Наименьших элементов во множестве может быть не более одного, в то время как минимальных может быть много. Легко показать, что если во множестве есть наименьший элемент, он является и единственным минимальным. Если же минимальных элементов несколько, то все они несравнимы.
Аналогично вводятся понятия максимального и наибольшего элементов.
Пример 1. Для множества подмножеств <x, y, z> с отношением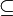 
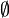
, изображённого на рисунке, единственным наименьшим и минимальным элементом является 
. Для множества непустых подмножеств наимешьшего нет, а минимальными будут <x>, <y>, <z>.
Пример 2. Для натуральных чисел с отношением делимости, единственным наименьшим и минимальным элементом является 1. Для натуральных чисел, больших 1, с тем же порядком, наименьшего элемента нет, а минимальными являются простые числа, т.к. они не делятся ни на какие другие элементы.
Строгий и нестрогий порядки
Иногда описанный здесь порядок называется нестрогим (или рефлексивным). В противовес ему существует понятие строгого (или иррефлексивного) частичного порядка — это отношение, удовлетворяющее только последним двум из приведённого списка аксиом.
Если R является нестрогим порядком, то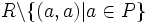 
— это соответствующий ему строгий порядок. Подобным образом и нестрогий порядок ставится в соответствие строгому.
Литература
Полезное
Смотреть что такое «Частичный порядок» в других словарях:
частичный порядок — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN partial order … Справочник технического переводчика
ЧАСТИЧНЫЙ ПОРЯДОК — см. Порядок … Математическая энциклопедия
Порядок Спорыньевые или Клавицепсовые (Саvicipitales) — Спорыньевые образуют перитеции в хорошо развитых стромах, состоящих только из гиф гриба. Стромы обычно мясистые, светло или яркоокрашенные, у некоторых представителей порядка темные. Их форма разнообразна, от распростертых но субстрату… … Биологическая энциклопедия
Порядок оплаты заказа — порядок расчетов, производимых туроператором со средством размещения, который включает полный или частичный авансовый платеж (предоплату); при этом окончательный расчет за предоставленные услуги производится по факту оказания данных услуг … Лексикон туриста
Полный порядок — В математике частично упорядоченным множеством называется множество, на котором определено отношение частичного порядка. Неформально можно сказать, что это отношение вводит некую иерархию элементов множества, выстраивает зависимости между ними,… … Википедия
Полный или частичный аванс — порядок оплаты, при котором туроператор перечисляет на счет средства размещения авансовый платеж за услуги, которые будут оказаны клиентам после получения аванса; аванс может составлять полную сумму стоимости услуг (полный аванс) или неполную… … Лексикон туриста
Упорядоченные и частично упорядоченные множества — (математичексие) множества, в которых каким либо способом установлен порядок следования их элементов или, соответственно, частичный порядок. Понятия порядка и частичного порядка следования элементов определяются следующим образом. Говорят … Большая советская энциклопедия
Теорема Шпильрайна — Теорема Шпильрайна одна из центральных теорем теории упорядоченных множеств, впервые сформулированная и доказанная польским математиком Эдвардом Шпильрайном в 1930 году. Содержание 1 Формулировка 2 Доказательство … Википедия
Упорядоченные и частично упорядоченные множества — В математике частично упорядоченным множеством называется множество, на котором определено отношение частичного порядка. Неформально можно сказать, что это отношение вводит некую иерархию элементов множества, выстраивает зависимости между ними,… … Википедия
ДОУПОРЯДОЧИВАЕМАЯ ГРУППА — группа, всякий частичный порядок в к рой может быть продолжен до линейного (см. Упорядочиваемая группа). Д. г. наз. также О* группами. Существует следующий критерий доупорядочиваемости группы. Пусть S(g) минимальная инвариантная подполугруппа… … Математическая энциклопедия
Упорядоченные множества
Каждому отношению порядка на множестве можно сопоставить следующие отношения.
Двойственный порядок
Отношение доминирования
Из определения следует, что отношение доминирования иррефлексивно, антисимметрично, но не транзитивно. Оно может быть и пусто. Например, легко видеть, что пустым будет отношение доминирования, если исходный порядок является плотным бинарным отношением на соответствующем множестве.
в. По отношению делимости на множестве натуральных чисел 15 доминирует над 3 и 5, но 20 не доминирует над 5, так как существует „промежуточный» элемент — 10, делитель 20, который делится на 5, но не равен ни 20, ни 5.
Упорядоченное подмножество
Упорядоченное множество, все элементы которого попарно сравнимы, называют линейно упорядоченным, а соответствующее отношение — отношением линейного порядка (или просто линейным порядком). Бели индуцированный порядок на подмножестве упорядоченного множества является линейным, то это линейно упорядоченное подмножество называют цепью. Любое подмножество попарно не сравнимых элементов данного упорядоченного множества называют антицепью.
Замечание 1.5. Обратим внимание на то, что термину «упорядоченное множество» (в смысле приведенного определения) отвечает термин «частично упорядоченное множество», а то, что мы называем линейно упорядоченным множеством, называется просто упорядоченным множеством. Терминология этого выпуска более принята в алгебраической литературе и литературе по дискретной математике. Употребление термина «частично упорядоченное множество» мотивировано желанием подчеркнуть, что в общем случае в упорядоченном множестве существуют не сравнимые элементы.
б. Отношение делимости (см. пример 1.13.г) на множестве и отношение включения на (см. пример 1.13,д) не являются линейными порядками, за исключением случая, когда — одноэлементное множество.
Наибольший, наименьший и максимальный, минимальный элементы множества
Замечание 1.6. Поскольку на одном и том же множестве могут быть определены разные отношения порядка (например, на множестве натуральных чисел — естественный числовой порядок и отношение делимости), то, когда это необходимо, мы будем говорить о наибольших, наименьших (соответственно максимальных и минимальных) элементах по данному отношению порядка, уточняя тем самым, о каком отношении порядка идет речь.
Следующие примеры показывают, что максимальных (минимальных) элементов может быть сколько угодно. Но заметим, что если у множества есть наибольший (соответственно наименьший) элемент, то он является единственным максимальным (соответственно минимальным) элементом данного множества.
Верхняя и нижняя грань множества
Множество всех верхних (нижних) граней множества называют верхним (нижним) конусом и обозначают (соответственно ).
Пример 1.18. а. Рассмотрим множество точек прямоугольника (рис. 1.11, б) с заданным в примере 1.17 отношением порядка. Точка является точной нижней гранью, а точка — точной верхней гранью этого множества. Обе точки принадлежат множеству.
Если рассмотреть множество (рис. 1.11, в) с тем же отношением порядка, то увидим, что точная нижняя грань (точка ) и точная верхняя грань (точка ) множества существуют, но не принадлежат множеству.
Вполне упорядоченные множества
Множество натуральных чисел с отношением естественного числового порядка вполне упорядоченное. Множество целых чисел не вполне упорядоченное, поскольку оно не имеет наименьшего элемента. Аналогично множества рациональных и действительных чисел не являются вполне упорядоченными.
Говорят также и о взаимно двойственных определениях: если в любом определении, связанном с упорядоченным множеством, произвести взаимные замены согласно принципу двойственности, то получится новое определение, называемое двойственным к исходному. Так, определение наибольшего (максимального) элемента множества двойственно к определению наименьшего (минимального) элемента, и наоборот. Часто употребляют оборот речи: «двойственным образом…» (или «двойственно…»), понимая под этим переход к утверждению или определению, которое двойственно к исходному.
Способы наглядного представления упорядоченных множеств
Рассмотрим теперь некоторые способы наглядного представления упорядоченных множеств.
На рис. 1.13 приведена диаграмма Хассе для упорядоченного множества всех подмножеств трехэлементного множества по отношению включения (см. пример 1.13.д).
Элемент а упорядоченного множества называют точной верхней гранью последовательности если он есть точная верхняя грань множества всех членов последовательности. Другими словами, точная верхняя грань последовательности есть точная верхняя грань области ее значений как функции натурального аргумента.
Точная нижняя грань последовательности
Двойственно определяется точная нижняя грань последовательности.
Упорядоченное множество называют индуктивным, если:
Например, множество всех подмножеств некоторого множества по отношению включения будет индуктивным. Наименьший элемент — пустое множество, а точной верхней гранью произвольной неубывающей последовательности множеств будет объединение всех членов этой последовательности (наименьшее по включению множество, содержащее в качестве подмножества любой член последовательности).
Теорема 1.6. Всякое непрерывное отображение одного индуктивного упорядоченного множества в другое монотонно.
В общем случае монотонное в смысле определения 1.6 отображение не является непрерывным в смысле определения 1.5. Приведем пример, показывающий, что утверждение, обратное теореме 1.6, неверно.
Пример 1.19. Рассмотрим множество всех точек отрезка числовой прямой с порядком, индуцированным естественным числовым порядком. Это множество индуктивно: его наименьший элемент — 0, а любая неубывающая последовательность элементов ограничена сверху и по признаку Вейерштрасса имеет предел, который и будет ее точной верхней гранью. Любая кусочно-непрерывная (но не непрерывная!) и монотонная в смысле обычных определений из курса математического анализа функция, отображающая этот отрезок на любой отрезок с порядком, индуцированным естественным числовым порядком, дает пример монотонного в смысле определения 1.6, но не непрерывного в смысле определения 1.5 отображения между индуктивными частично упорядоченными множествами. Например, пусть функция имеет вид
Не следует путать отображение, монотонное в смысле определения 1.6, с монотонными функциями из курса математического анализа. Функция будет монотонной в смысле определения 1.6 тогда и только тогда, когда она является неубывающей.
Для приложений особенно важны непрерывные отображения индуктивного упорядоченного множества в себя.