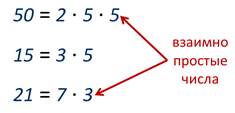
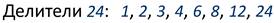Что такое наибольший общий делитель взаимно простые числа

Взаимно простые числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение взаимно простых чисел

Сначала определимся, что значит простое число.

Главное свойство простых чисел в том, что простое число делится только на единицу и на само себя.

Таких чисел немного, большинство все-таки можно разделить на другие числа. В простых числах самое важное — это деление нацело. Дробные частные и деление с остатком не рассматриваем.

Понятие взаимно простых чисел можно применить для двух целых чисел или для большего количества. Сформулируем, какие числа называются взаимно простыми.

Взаимно простые числа

Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице — то есть НОД (a, b) = 1.

Проще говоря, взаимно простые числа — это целые числа, у которых нет общих делителей, кроме единицы.

Наибольшим общим делителем двух чисел a и b называется наибольшее число, на которое a и b делятся без остатка. Для записи может использоваться аббревиатура НОД. Для двух чисел можно записать так: НОД (a, b).

Наибольший общий делитель взаимно простых чисел — это единица, что следует из определения взаимно простых чисел.

Приведем примеры взаимно простых чисел.

Заметим, что два простых числа всегда являются взаимно простыми. Однако, два числа не обязательно должны быть простыми, чтобы быть взаимно простыми. Вот такая математика в 5 классе. И еще раз: либо одно из них, либо они оба могут быть составными и при этом являться взаимно простыми. Приведем пример.

Делители 8: ±1, ±2, ±4, ±8.

На математике в 5 и 6 класса часто встречаются задания, в которых нужно доказать, что конкретные целые числа являются взаимно простыми. Из чего обычно состоит такое доказательство:

Перед вычислением НОД можно заглянуть в таблицу простых чисел и проверить, вдруг исходные целые числа можно назвать простыми. Тогда решение будет проще, так как мы знаем, что НОД простых чисел равен единице.

Повторим еще раз. Что значит взаимно простые числа? Это целые числа, у которых нет общих делителей, кроме единицы.

Пример 1

Доказать, что числа 84 и 275 являются взаимно простыми.

Сверяемся с таблицей простых чисел. 84 и 275 не являются простыми, поэтому нельзя сразу сказать об их взаимной простоте.

Вычислим НОД. Используем алгоритм Евклида для нахождения НОД:

Доказали, что числа 84 и 275 взаимно простые.

Определение взаимно простых чисел можно расширить для трех и большего количества чисел.

То есть если у некоторого набора целых чисел есть положительный общий делитель, отличный от единицы, то эти целые числа не являются взаимно простыми.

Любая совокупность простых чисел составляет набор взаимно простых чисел, например, 2, 3, 11, 19, 151, 293 и 677 — взаимно простые числа. А четыре числа 12, −9, 900 и −72 не являются взаимно простыми, так как у них есть положительный общий делитель 3. Числа 17, 85 и 187 тоже не взаимно простые, потому что каждое из них можно разделить на 17.

Как определить взаимно простые числа:

Пример 2

Являются ли числа 331, 463 и 733 взаимно простыми?

Заглянем в таблицу простых чисел. Видим, что 331, 463 и 733 — простые. Значит, у них есть единственный положительный общий делитель — единица. Поэтому, 331, 463 и 733 есть взаимно простые числа.

Пример 3

Доказать, что числа −14, 105, −2 107 и −91 не являются взаимно простыми.

Найдем НОД заданных чисел и убедимся, что он не равен единице.

Делители целых отрицательных чисел совпадают с делителями соответствующих противоположных чисел. Поэтому НОД (−14, 105, 2 107, −91) = НОД (14, 105, 2 107, 91). Посчитаем:

НОД (14, 105, 2 107, 91) = 7.

Мы получили, что наибольший общий делитель исходных чисел равен семи, поэтому эти числа не являются взаимно простыми. Доказали.

Свойства взаимно простых чисел

У взаимно простых чисел есть определенные свойства. Рассмотрим основные свойства взаимно простых чисел.

Свойство 1

Числа, которые получились при делении целых чисел a и b на их наибольший общий делитель, называются взаимно простыми. То есть, a : НОД (a, b) и b : НОД (a, b) — взаимно простые.

Это свойство взаимно простых чисел помогает находить пары взаимно простых чисел. Для этого достаточно взять два любых целых числа и разделить их на наибольший общий делитель. В результате получим взаимно простые числа.

Свойство 2

Докажем эту необходимость:

Пусть числа a и b взаимно простые. Тогда по определению взаимно простых чисел НОД (a, b) = 1. А из свойств НОД мы знаем, что для целых чисел a и b верно соотношение Безу au₀ + bv₀ = НОД (a, b). Следовательно, au₀ + bv₀ = 1.

Соотношение Безу — представление НОД целых чисел в виде их линейной комбинации с целыми коэффициентами.

Докажем достаточность:

Свойство 3

Если числа a и b взаимно простые, и произведение ac делится на b — значит c делится на b.

Действительно, так как a и b взаимно простые, то из предыдущего свойства у нас есть равенство au₀ + bv₀ = 1. Если умножть обе части этого равенства на c, получится acu₀ + bcv₀ = c.

Первое слагаемое суммы acu₀ + bcv₀ делится на b, так как ac делится на b по условию, второе слагаемое этой суммы также делится на b, так как один из множителей равен b. Можно сделать вывод, что вся сумма делится на b. А так как сумма acu₀ + bcv₀ равна c, то и c делится на b.

Свойство 4

Если числа a и b взаимно простые, то НОД (ac, b) = НОД (c, b).

Покажем, во-первых, что НОД (ac, b) делит НОД (c, b), а во-вторых, что НОД (c, b) делит НОД (ac, b), это и будет доказывать равенство НОД (ac, b) = НОД (c, b).

НОД (ac, b) делит и ac и b, а так как НОД (ac, b) делит b, то он также делит и bc. То есть, НОД (ac, b) делит и ac и bc, следовательно, в силу свойств наибольшего общего делителя он делит и НОД (ac, bc), который по свойствам НОД равен c * НОД (a, b) = c. Таким образом, НОД (ac, b) делит и b и c, следовательно, делит и НОД (c, b).

С другой стороны, НОД (c, b) делит и c и b, а так как он делит с, то также делит и ac. Поэтому НОД (c, b) делит и ac и b, следовательно, делит и НОД (ac, b).

Так мы показали, что НОД (ac, b) и НОД (c, b) взаимно делят друг друга, значит, они равны.

Свойство 5

Предыдущее свойство взаимно простых чисел поможет намзаписать ряд равенств вида:

Определение попарно простых чисел

Через взаимно простые числа можно дадим определение попарно простых чисел.

Приведем пример попарно простых чисел.

При этом, взаимно простые числа далеко не всегда могут быть попарно простыми. Подтвердим на примере. 8, 16, 5 и 15 не являются попарно простыми, так как числа 8 и 16 не взаимно простые. Однако, 8, 16, 5 и 15 — взаимно простые. Таким образом, 8, 16, 5 и 15 — взаимно простые, но не попарно простые.

Остановимся на понятии совокупности некоторого количества простых чисел. Эти числа всегда являются и взаимно простыми и попарно простыми. Например, 71, 443, 857, 991 — и попарно простые, и взаимно простые.

Когда речь идет о двух целых числах, то для них понятия «попарно простые» и «взаимно простые» совпадают.

Источник

Наибольший общий делитель (НОД), свойства и формулы

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие наибольшего общего делителя

Начнем с самого начала и вспомним, что такое общий делитель. У целого числа может быть несколько делителей. А сейчас нам особенно интересно, как обращаться с делителями сразу нескольких целых чисел.

Делитель натурального числа — это такое натуральное число, которое делит данное число без остатка. Если у натурального числа больше двух делителей, его называют составным.

Если b — делитель целого числа a, которое не равно нулю, то модуль числа b не может быть больше модуля числа a. Значит любое число, не равное 0, имеет конечное число делителей.

Наибольшим общим делителем двух чисел a и b называется наибольшее число, на которое a и b делятся без остатка. Для записи может использоваться аббревиатура НОД. Для двух чисел можно записать вот так: НОД (a, b).

Проверить результаты вычислений можно с помощью онлайн-калькулятора НОД и НОК.

Наибольшим общим делителем трех чисел и более будет самое большое целое число, которое будет делить все эти числа одновременно.

Взаимно простые числа — это натуральные числа, у которых только один общий делитель — единица. Их НОД равен 1.

Помимо НОД есть еще и НОК, что расшифровывается, как наименьшее общее кратное и означает наименьшее число, которое делится на каждое из исходных чисел без остатка.

Еще один пример. Рассчитаем НОД для 28 и 64.

Д (64) = 2 * 2 * 2 * 2 * 2 * 2

НОД (28; 64) = 2 * 2 = 4

Ответ: НОД (28; 64) = 4

Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.

Свойства наибольшего общего делителя

У наибольшего общего делителя есть ряд определенных свойств. Опишем их в виде теорем и сразу приведем доказательства.

Важно! Все свойства НОД будем формулировать для положительных целых чисел, при этом будем рассматривать делители только больше нуля.

Свойство 1. Наибольший общий делитель чисел а и b равен наибольшему общему делителю чисел b и а, то есть НОД (a, b) = НОД (b, a). Перемена мест чисел не влияет на конечный результат.

Доказывать свойство не имеет смысла, так как оно напрямую исходит из самого определения НОД.

Свойство 2. Если а делится на b, то множество общих делителей чисел а и b совпадает со множеством делителей числа b, поэтому НОД (a, b) = b.

Доказательство

Любой общий делитель чисел а и b является делителем каждого из этих чисел, в том числе и числа b. Так как а кратно b, то любой делитель числа b является делителем и числа а, благодаря свойствам делимости. Из этого следует, что любой делитель числа b является общим делителем чисел а и b.

Значит, если а делится на b, то совокупность делителей чисел а и b совпадает с совокупностью делителей одного числа b. А так как наибольшим делителем числа b является само число b, то наибольший общий делитель чисела и b также равен b, то есть НОД (а, b) = b.

В частности, если a = b, то НОД (a, b) = НОД (a, a) = НОД (b, b) = a = b.

Доказанное свойство наибольшего делителя можно использовать, чтобы найти НОД двух чисел, когда одно из них делится на другое. При этом НОД равен одному из этих чисел, на которое делится другое число.

Свойство 3. Если a = bq + c, где а, b, с и q — целые числа, то множество общих делителей чисел а и b совпадает со множеством общих делителей чисел b и с. Равенство НОД (a, b) = НОД (b, c) справедливо.

Доказательство

Существует равенство a = bq + c, значит всякий общий делитель чисел а и b делит также и с, исходя из свойств делимости. По этой же причине, всякий общий делитель чисел b и с делит а. Поэтому совокупность общих делителей чисел а и b совпадает с совокупностью общих делителей чисел b и c.

Поэтому должны совпадать и наибольшие из этих общих делителей, и равенство НОД (a, b) = НОД (b, c) можно считать справедливым.

Свойство 4. Если m — любое натуральное число, то НОД (mа, mb) = m * НОД(а, b).

Доказательство

Если умножить на m обе стороны каждого из равенств алгоритма Евклида, то получим, что НОД (mа, mb)= mr, где r — это НОД (а, b). На этом свойстве наибольшего общего делителя основан поиск НОД с помощью разложения на простые множители.

Свойство 5. Пусть р — любой общий делитель чисел а и b, тогда НОД (а : p, b : p) = НОД (а, b) : p. А именно, если p = НОД (a, b) имеем НОД (a : НОД (a, b), b: НОД (a, b)) = 1, то есть, числа a : НОД (a, b) и b : НОД (a, b) — взаимно простые.

Так как a = p(a : p) и b = p(b : p), и в силу предыдущего свойства, мы можем записать цепочку равенств вида НОД (a, b) = НОД (p(a : p), p(b : p)) = p * НОД (a : p, b : p), откуда и следует доказываемое равенство.

Способы нахождения наибольшего общего делителя

Найти наибольший общий делитель можно двумя способами. Рассмотрим оба, чтобы при решении задач выбирать самую оптимальную последовательность действий.

1. Разложение на множители

Чтобы найти НОД нескольких чисел, достаточно разложить их на простые множители и перемножить между собой общие множители для всех чисел.

Пример 1. Найти НОД (84, 90).

Ответ: НОД (84, 90) = 6.

Пример 2. Найти НОД (15, 28).

Ответ: НОД (15, 28) = 1.

Пример 3. Найти НОД для 24 и 18.

Ответ: НОД (24, 18) = 6

2. Алгоритм Евклида

Способ Евклида помогает найти НОД через последовательное деление. Сначала посмотрим, как работает этот способ с двумя числами, а затем применим его к трем и более.

Алгоритм Евклида заключается в следующем: если большее из двух чисел делится на меньшее — наименьшее число и будет их наибольшим общим делителем. Использовать метод Евклида можно легко по формуле нахождения наибольшего общего делителя.

Формула НОД: НОД (a, b) = НОД (b, с), где с — остаток от деления a на b.

Пример 1. Найти НОД для 24 и 8.

Так как 24 делится на 8 и 8 тоже делится на 8, значит, 8 — общий делитель этих чисел. Этот делитель является наибольшим, потому что 8 не может делиться ни на какое число, большее его самого. Поэтому: НОД (24, 8) = 8.

В остальных случаях для нахождения наибольшего общего делителя двух чисел нужно соблюдать такой порядок действий:

Пример 2. Найти наибольший общий делитель чисел 140 и 96:

Последний делитель равен 4 — это значит: НОД (140, 96) = 4.

Ответ: НОД (140, 96) = 4

Пошаговое деление можно записать столбиком:

Чтобы найти наибольший общий делитель трех и более чисел, делаем в такой последовательности:

Знакомство с темой наибольшего общего делителя начинается в 5 классе с теории и закрепляется в 6 классе на практике. В этой статье мы узнали все основные определения, свойства и их доказательства, а также как найти НОД.

Источник

Урок 6 Бесплатно Наибольший общий делитель. Взаимно простые числа

Сейчас мы научимся определять наибольший общий делитель для двух или трех чисел, познакомимся с алгоритмом Евклида и узнаем много всего интересного.

Наибольший общий делитель

Самое большое натуральное число, на которое делятся нацело два или более чисел, называется их наибольшим общим делителем (НОД).

При поиске НОД, например, 36 и 24, надо:

1. Записать их в виде разложения на простые множители

3. Вычислить произведение множителей, которые остались: \(\mathbf<2\cdot2\cdot3 = 12>\)

В итоге НОД чисел 36 и 24 равен 12.

Если при нахождении НОДа среди чисел есть одно, на которое делятся все остальные, то оно и будет тем самым НОДом.

Например, у чисел 12, 36 и 48 НОД = 12

Пример 1

Найдите все общие делители чисел:

А) 70, 105

Б) 18, 24

В) 45,75

Г) 324, 111, 432

Д) 320, 640, 960

Решение

Пример 2

На новогоднем утреннике дети получили пакеты с подарками. Всего во всех пакетах находилось 159 апельсинов и 106 яблок. Сколько детей было на новогодней ёлке? Сколько в каждом пакете было яблок и сколько апельсинов?

Решение

Ребят на елке было 53 человека. В каждом пакете подарка было по 3 апельсина и 2 яблока.

Пример 3

Для выезда на природу работникам предоставили несколько автобусов. В каждом автобусе равное число мест для сидения. 184 человека выехали в лес, а 138 отправились на озеро. Так вышло, что все места в автобусах были заняты, и, стоя, никто не ехал. Сколько автобусов было и сколько пассажиров ехало в каждом из них?

Решение

В каждом автобусе было по 23 места. В лес поехало 8 автобусов, а на озеро поехало 6 автобусов. Всего было 8 + 6 = 14 автобусов.

У меня есть дополнительная информация к этой части урока!

Всё достаточно просто: взять пару положительных чисел и получить по правилу новую пару, которая будет состоять из меньшего числа и разницы между большим и меньшим числом. Повторять алгоритм до тех пор, пока числа не получатся одинаковыми. Последнее число и будет НОДом первоначальной пары чисел.

Евклид предложил алгоритм только для натуральных чисел и геометрических величин (длин, площадей, объёмов). Однако в XIX веке он был обобщён на другие типы математических объектов, включая целые числа Гаусса и полиномы от одной переменной.

Пройти тест и получить оценку можно после входа или регистрации

Взаимно простые числа

Давайте разберёмся с некоторыми натуральными числами.

Число 15 имеет делители 1, 3, 5, а число 16 имеет делители 1, 2, 4, 8

Рассмотрев этот и другие примеры, не сложно догадаться, что натуральные числа, у которых НОД равен 1, называются взаимно простые.

Пример 1

Возьмем две пары чисел 12 и 18, 13 и 21. Выясним, есть ли среди них взаимно простые числа. Для этого каждое из чисел распишем по простым делителям.

12 имеет делители 1, 2, 3, 4, 6, 12

18 имеет делители 1, 2, 3, 6, 9, 18

Значит, числа 12 и 18 кроме единицы имеют общие делители 2, 3, 6, поэтому они не являются взаимно простыми числами. Повторим действия с другой парой чисел 13 и 21.

Число 13 делится нацело на 1, 13, а число 21 делится нацело на 1, 3, 7, 21.

Значит, вторая пара чисел состоит из взаимно простых.

Пример 2

Пусть у нас есть два числа 45 и 32, которые являются натуральными и составными.

Первое из них 45 имеет делители 1, 3, 5, 9, 15, 45, а натуральное число 32 имеет делители 1, 2, 4, 8, 16, 32

Оба числа из этой пары имеют единственный общий делитель- 1

Значит, числа 45 и 32 являются взаимно простыми. Запишем оба числа в виде разложения на простые множители

Числа из нашего примера, 45 и 32, в записи на множители не содержат равных чисел. Значит, разложения на простые множители двух и более взаимно простых чисел не включают одинаковых простых множителей.

Пример 3

Являются ли взаимно простыми числа:

А) 55 и 40

Б) 77 и 92

В) 14, 32 и 41

Г) 231 и 298

Д) 68 и 137

Решение:

Нет, не являются взаимно простыми числами

Да, являются взаимно простыми числами

Да, являются взаимно простыми числами

Да, являются взаимно простыми числами

Да, являются взаимно простыми числами

Пример 4

Найдите разложение на простые множители наибольшего общего делителя чисел a и b, если:

Решение

Признак делимости на произведение взаимно простых чисел: если данное натуральное число делится на каждое из взаимно простых чисел, то оно делится и на их произведение.

Рассмотрим этот признак на примере трех взаимно простых чисел.

Возьмем, например, 420.

Число 420 без остатка делится на 2, на 5 и на 7.

Числа 2, 5, 7 являются взаимно простыми (так как их НОД равен 1). Проверим, будет ли делиться 420 на произведение взаимно простых чисел 2, 5 и 7.

Очевидно, что 420 делится нацело на произведение чисел двух, пяти и семи.

Правило можно применять для любого количества множителей.

Пройти тест и получить оценку можно после входа или регистрации

Интересная информация

Алгоритм Евклида, который используется для нахождения НОДа и с которым мы познакомились выше, широко применяется при решении других математических задач. Например, он связан с цепными дробями и позволяет с их помощью уменьшать большие дроби до маленьких.

Кроме того, алгоритм используется при решении линейных диофантовых уравнений. Это такие уравнения, у которых могут быть несколько неизвестных целых величин, и все их нужно найти. Например, может быть такое уравнение:

Решением этого уравнения будет пара чисел

Могут быть и другие пары решений. Решение таких уравнений начинается обычно с нахождения НОДа чисел, стоящих перед неизвестными. В нашем случае мы бы находили \(\mathbf<НОД(2, 3)>\)

Не всегда данный алгоритм позволяет быстро решать задачи. Иногда можно потратить много времени, сделать много вычислений, прежде чем найти нужный результат. Это единственный большой минус одного из старейших численных алгоритмов.

Заключительный тест

Пройти тест и получить оценку можно после входа или регистрации

Источник

Наибольший общий делитель. Взаимно простые числа

Урок 6. Математика 6 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Наибольший общий делитель. Взаимно простые числа»

На данном уроке мы продолжим работу с делителями числа. Напомним, что делителем натурального числа а называют натуральное число, на которое а делится без остатка.

Рассмотрим простой случай. Саша и Маша решили украсить кабинет осенними букетами из сухих листьев. Саша собрал 12 кленовых листьев. Маша принесла 18 листьев каштана.

«А как нам узнать, какое количество букетов мы сможем составить, чтобы в каждом клиновых листьев было одинаковое количество, да и листьев каштана во всех букетах было поровну?» – спросил Саша.

«Каждое из чисел 12 и 18 должно делиться на число букетов» – ответила Маша. – «Поэтому выпишем все делители этих чисел».

Попробуем перевести эту задачу на математический язык.

Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем этих чисел.

Наибольший общий делитель двух чисел обозначается НОД (по первым буквам слов «Наибольший Общий Делитель»).

Наибольший общий делитель чисел 12 и 18 равен 6.

Теперь найдём НОД чисел 26 и 45.

Обратите внимание, что существуют числа, у которых только один общий делитель: единица. Такие числа называют взаимно простыми.

Таким образом, числа называются взаимно простыми, если у них нет общих делителей кроме единицы.

НОД взаимно простых чисел равен 1.

Чтобы находить наибольший общий делитель, не обязательно перебирать все делители чисел. В некоторых случаях это очень долгая и кропотливая работа. Существует другой способ.

Чтобы найти наибольший общий делитель двух чисел надо: разложить каждое из чисел на простые множители.

Обратите внимание, как интересно получается: сами числа составные, а вот между собой – взаимно простые.

Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем этих чисел.

Наибольший общий делитель двух чисел обозначается НОД по первым буквам слов «Наибольший Общий Делитель».

Если у нескольких чисел нет общих делителей кроме единицы, то эти числа называются взаимно простыми. НОД взаимно простых чисел равен 1.

Источник