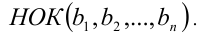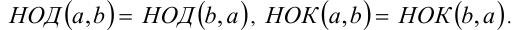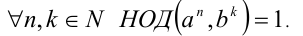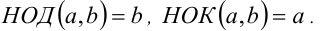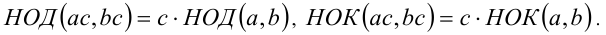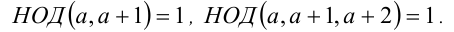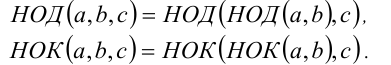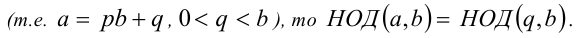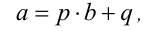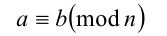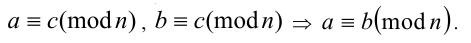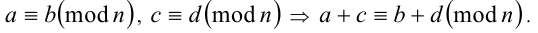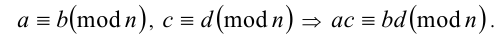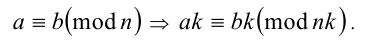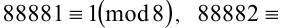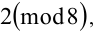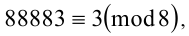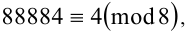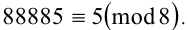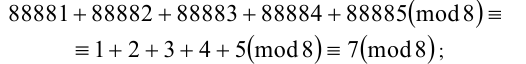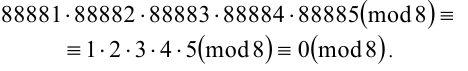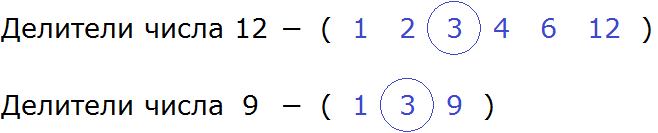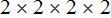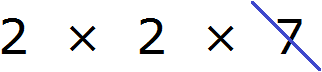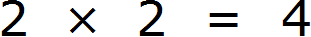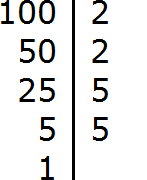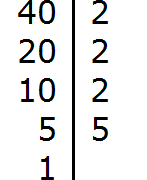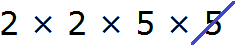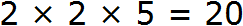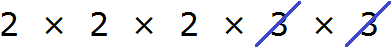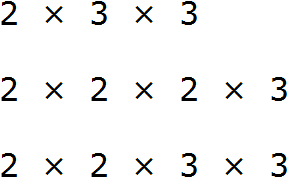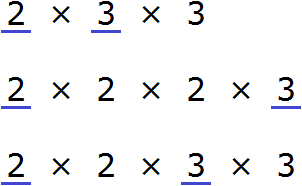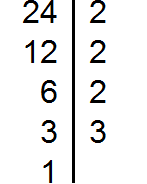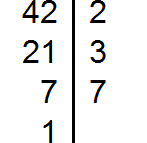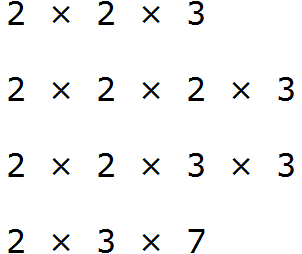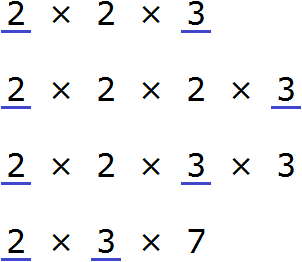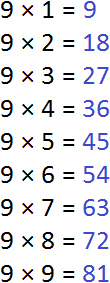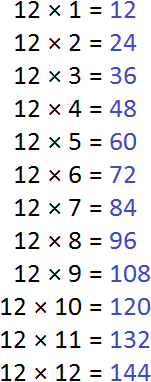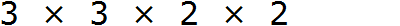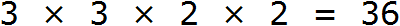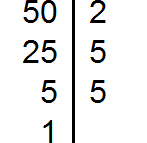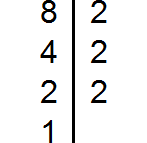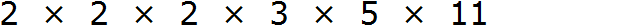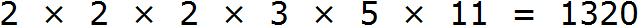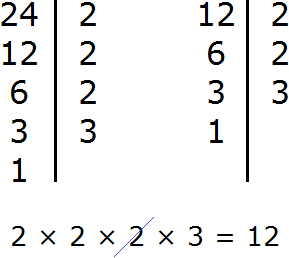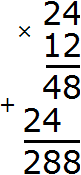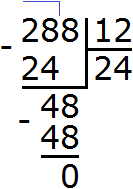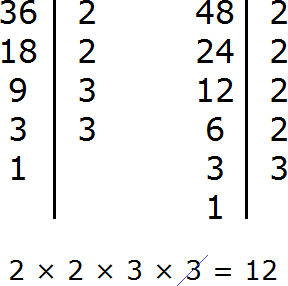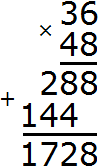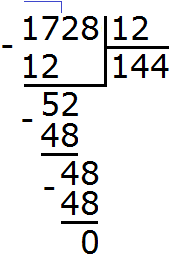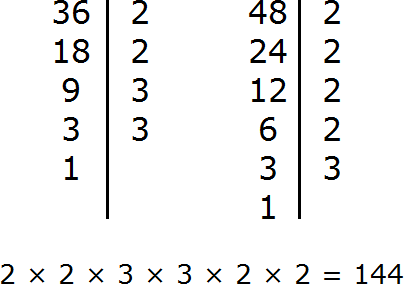Что такое наибольший общий кратное двух натуральных

Наибольший общий делитель, наименьшее общее кратное, алгоритмы их нахождения и свойства

Наибольший общий делитель, наименьшее общее кратное, алгоритмы их нахождения и свойства

Сформулируем несколько определений, имеющих отношение к понятиям наибольшего общего делителя и наименьшего общего кратного.

Если два или несколько натуральных чисел не имеют общих натуральных делителей, отличных от единицы, то эти числа называются взаимно простыми. При этом каждое из них в отдельности не обязательно должно быть простым. Например, числа 7 и 9 — взаимно простые; 4, 5 и 6 — взаимно простые.

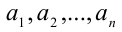
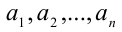
Так как числа могут иметь лишь конечное число общих натуральных делителей, то среди них всегда имеется наибольший, который называется наибольшим общим делителем и обозначается НОД. В случае взаимно простых чисел он равен единице.

Рассмотрим стандартный алгоритм нахождения НОД ()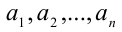

1) Разложим каждое из чисел 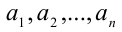на простые множители;

2) перебирая все различные простые множители, входящие хотя бы в одно из этих чисел, возьмём каждый из них в наименьшей степени, с которой он входит в числа ;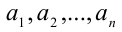

3) перемножим взятые множители (с наименьшими степенями вхождения). Полученное число и будет НОД( ).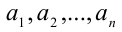

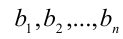
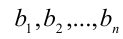
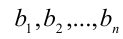
Если натуральное число а является кратным для каждого из чисел (т.е. делится на любое из этих чисел нацело), то а называется общим кратным чисел . В частности, произведение нескольких натуральных чисел всегда является их общим кратным. Среди всех общих кратных данных чисел(их бесконечно много) всегда имеется наименьшее; оно называется наименьшим общим кратным и обозначается

Стандартный алгоритм нахождения наименьшего общего кратного нескольких чисел состоит в следующем:

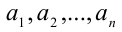
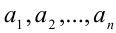
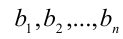
Можно определить понятия наибольшего общего делителя и наименьшего общего кратного для произвольных целых (ненулевых, но не обязательно натуральных) чисел. Так, наибольшим общим делителем целых чисел называется такой положительный общий делитель чисел , который делится на любой другой общий делитель этих чисел. Наименьшим общим кратным отличных от нуля целых чисел называется наименьшее положительное число, кратное всем этим числам.

Как уже отмечалось, отыскание НОД двух натуральных чисел а и b требует предварительного разложения этих чисел на простые множители. Это несложно сделать, если числа невелики, но разложить на множители многозначные числа бывает трудно. Существует способ отыскания НОД, требующий лишь умения делить с остатком (см. следующий пункт). Этот способ предложил в свое время Евклид, поэтому он называется алгоритмом Евклида и основан на следующих утверждениях.

Перечислим наиболее важные свойства НОД и НОК, позволяющие лучше изучить природу этих понятий.

Свойства НОД и НОК

Для любых натуральных a,b,C,d справедливы следующие свойства.

2. В частности, если то (свойство верно только для двух чисел а,b).

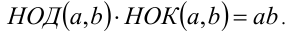
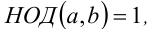
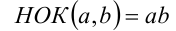
4. Если 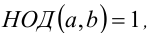то

5. Если 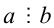, то

6.Общий множитель С можно выносить из-под знаков НОД и НОК:

7.Два (три) последовательных натуральных числа взаимно просты:

8.Пошаговое (,последовательное) вычисление НОД и НОК:

9.Если b > а , то НОД(а,Ь)= НОД(а,b- а).

10. Если при делении числа а на число b получается ненулевой остаток q

Знание указанных свойств позволяет на практике упрощать решение многих задач, в которых используются понятия НОД и НОК.

Деление с остатком

Пусть имеются два числа а и b 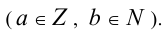Разделить целое число а на натуральное число b с остатком значит найти два целых числа р и q таких, что справедливо равенство

Сравнимость по модулю

и читают: « а равно b по модулю п ».

Можно доказать, например, что введённая таким образом операция сравнения обладает следующими свойствами.

1. Два числа, сравнимые с третьим по одному и тому же модулю, сравнимы между собой (по этому же модулю):

2. Сравнения по одному модулю можно складывать:

3.Сравнения по одному модулю можно почленно перемножать:

4. Обе части сравнения и модуль можно умножить на одно и то же целое число:

В следующей задаче эффективно используются некоторые из свойств операции сравнения по модулю.

Пример №1.

Найти остатки от деления на 8:

1) суммы 88881 + 88882 + 88883 + 88884 + 88885,

Решение:

1) Числа 88881,88882,88883,88884,88885 при делении на 8 дают соответственно остатки 1,2,3,4,5. То есть

Тогда по свойству 2 имеем

2) По свойству 3 имеем

Ответ: остаток от деления суммы на 8 равен 7; остаток от деления произведения на 8 равен 0.

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Как найти наименьшее общее кратное, НОК для двух и более чисел

Школьникам задают немало заданий по математике. Среди них очень часто встречаются задачи с такой формулировкой: имеются два значения. Как найти наименьшее общее кратное для заданных чисел? Необходимо уметь выполнять такие задания, поскольку полученные навыки применяют для работы с дробями при разных знаменателях. В статье разберем, как найти НОК и основные понятия.

Основные понятия

Прежде чем найти ответ на вопрос как находить НОК, нужно определиться с термином кратное. Чаще всего формулировка этого понятия звучит следующим образом: кратным некоторому значению А называют такое натуральное число, которое без остатка будет делиться на А. Так, для 4 кратными будут 8, 12, 16, 20 и так далее, до необходимого предела.

При этом количество делителей для конкретного значения может быть ограниченным, а кратных бесконечно много. Также есть такая же величина для натуральных значений. Это такой показатель, которое делится на них без остатка. Разобравшись с понятием самого меньшего значения для определенных показателей, перейдем к тому, как его находить.

Находим НОК

Наименьшее кратное двух или больше показателей является наименьшим натуральным числом, которое целиком делится на все указанные числа.

Существует несколько способов найти такое значение, рассмотрим следующие способы:

Теперь мы знаем, какова общая методика нахождения самого небольшого значения для двух, трех и более значений. Однако есть и частные методы, помогающие искать НОК, если предыдущие не помогают.

Как находить НОД и НОК.

Частные способы нахождения

Как и для любого математического раздела, имеются частные случаи нахождения НОК, которые помогают в специфических ситуациях:

Частные случаи встречаются реже, нежели стандартные примеры. Но благодаря им можно научиться работать с дробями различной степени сложности. Особенно это актуально для дробей, где имеются неодинаковые знаменатели.

Немного примеров

Разберем несколько примеров, благодаря которым можно понять принцип нахождения наименьшего кратного:

Благодаря примерам можно понять, как находится НОК, какие есть нюансы и в чем заключается смысл таких манипуляций.

Находит НОК гораздо проще, чем может показаться изначально. Для этого применяется как простое разложение, так и умножение простых значений друг на друга. Умение работать с данным разделом математики помогает при дальнейшем изучении математических тем, в особенности дробей разной степени сложности.

Не забывайте периодически решать примеры различными методами, это развивает логический аппарат и позволяет запомнить многочисленные термины. Изучайте методы нахождения такого показателя и вы сможете хорошо работать с остальными математическими разделами. Удачного изучения математики!

Видео

Это видео поможет вам понять и запомнить, как находить наименьшее общее кратное.

Источник

Наименьшее общее кратное

Общее кратное

Число может быть кратно не одному, а сразу нескольким числам, такое число называется общим кратным данных чисел.

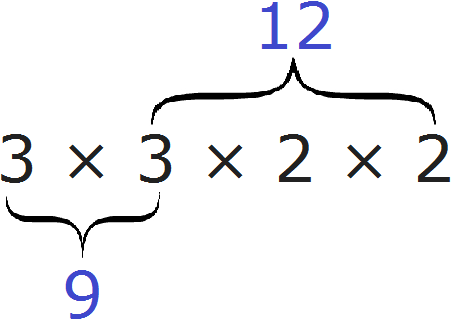
Числу 3 кратны числа: 6, 9, 12, 15 и т. д.

Числу 4 кратны числа: 8, 12, 16, 20 и т. д.

Можно заметить, что одно и тоже число (12) делится нацело сразу на оба числа 3 и 4. Следовательно, число 12 есть общее кратное чисел 3 и 4.

Общее кратное чисел — это любое число, которое делится без остатка на каждое из данных чисел.

Найти общее кратное нескольких натуральных чисел достаточно легко, можно просто перемножить данные числа, полученное произведение и будет их общим кратным.

Пример. Найти общее кратное для чисел 2, 3, 4, 6.

Число 144 — общее кратное чисел 2, 3, 4 и 6.

Для любого количества натуральных чисел существует бесконечно много кратных.

Пример. Для чисел 12 и 20 кратными будут числа: 60, 120, 180, 240 и т. д. Все они являются общими кратными для чисел 12 и 20.

Наименьшее общее кратное

Наименьшее общее кратное (НОК) нескольких чисел — это самое маленькое натуральное число, которое делится без остатка на каждое из этих чисел.

Пример. Наименьшим общим кратным чисел 3, 4 и 9 является число 36, никакое другое число меньше 36 не делится одновременно на 3, 4 и 9 без остатка.

Наименьшее общее кратное записывается так:

Числа в круглых скобках могут быть указаны в любом порядке.

Пример. Запишем наименьшее общее кратное чисел 3, 4 и 9:

Как найти НОК

Рассмотрим два способа нахождения наименьшего общего кратного: с помощью разложения чисел на простые множители и нахождение НОК через НОД.

С помощью разложения на простые множители

Чтобы найти НОК нескольких натуральных чисел, надо разложить эти числа на простые множители, затем взять из этих разложений каждый простой множитель с наибольшим показателем степени и перемножить эти множители между собой.

Пример. Найдите наименьшее общее кратное двух чисел 99 и 54.

Решение: разложим каждое из этих чисел на простые множители:

Наименьшее общее кратное должно делиться на 99, значит, в его состав должны входить все множители числа 99. Далее НОК должно делиться и на 54, т. е. в его состав должны входить множители и этого числа.

Выпишем из этих разложений каждый простой множитель с наибольшим показателем степени и перемножим эти множители между собой. Получим следующее произведение:

Это и есть наименьшее общее кратное данных чисел. Никакое другое число меньше 594 не делится нацело на 99 и 54.

Ответ: НОК (99, 54) = 594.

Так как взаимно простые числа не имеют одинаковых простых множителей, то их наименьшее общее кратное равно произведению этих чисел.

Пример. Найдите наименьшее общее кратное двух чисел 12 и 49.

Решение: разложим каждое из этих чисел на простые множители:

12 = 2 · 2 · 3 = 2 2 · 3,

Применяя к этому случаю правило, мы придём к заключению, что взаимно простые числа надо просто перемножить:

2 2 · 3 · 7 2 = 12 · 49 = 980.

Ответ: НОК (12, 49) = 980.

Таким же образом надо поступать, когда нужно найти наименьшее общее кратное простых чисел.

Пример. Найдите наименьшее общее кратное чисел 5, 7 и 13.

Решение: так как данные числа являются простыми, то просто перемножим их:

Ответ: НОК (5, 7, 13) = 455.

Если большее из данных чисел делится на все остальные числа, то это число и будет наименьшим общим кратным данных чисел.

Пример. Найдите наименьшее общее кратное чисел 24, 12 и 4.

Решение: разложим каждое из этих чисел на простые множители:

24 = 2 · 2 · 2 · 3 = 2 3 · 3,

12 = 2 · 2 · 3 = 2 2 · 3,

Можно заметить, что разложение большего числа содержит все множители остальных чисел, значит большее из этих чисел делится на все остальные числа (в том числе и само на себя) и является наименьшим общим кратным:

Ответ: НОК (24, 12, 4) = 24.

Нахождение НОК через НОД

НОК двух натуральных чисел равно произведению этих чисел, поделённого на их НОД.

Правило в общем виде:

Пример. Найдите наименьшее общее кратное двух чисел 99 и 54.

Теперь мы можем вычислить НОК этих чисел по формуле:

НОК (99, 54) = 99 · 54 : НОД (99, 54) = 5346 : 9 = 594.

Ответ: НОК (99, 54) = 594.

Чтобы найти НОК трёх или более чисел используется следующий порядок действий:

Пример. Найдите наименьшее общее кратное чисел 8, 12 и 9.

Решение: сначала находим наибольший общий делитель любых двух из этих чисел, например, 12 и 8:

Вычисляем их НОК по формуле:

НОК (12, 8) = 12 · 8 : НОД (12, 8) = 96 : 4 = 24.

Теперь найдём НОК числа 24 и оставшегося числа 9. Их НОД:

Вычисляем НОК по формуле:

НОК (24, 9) = 24 · 9 : НОД (24, 9) = 216 : 3 = 72.

Ответ: НОК (8, 12, 9) = 72.

Калькулятор НОК

Источник

НОД и НОК

Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.

НОД — это наибольший общий делитель.

НОК — это наименьшее общее кратное.

Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.

Наибольший общий делитель

Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.

Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:

Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.

Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.

Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.

Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.

Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.

Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.

12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)

12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)

12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)

12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)

12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)

12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)

12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)

12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)

12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)

12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)

12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)

12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)

Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9

9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)

9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)

9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)

9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)

9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)

9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)

9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)

9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)

9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)

Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:

Выписав делители, можно сразу определить какой является наибольшим и общим.

Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3

И число 12 и число 9 делятся на 3 без остатка:

Значит НОД (12 и 9) = 3

Второй способ нахождения НОД

Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.

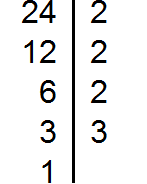
Пример 1. Найти НОД чисел 24 и 18

Сначала разложим оба числа на простые множители:

Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.

Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:

Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.

Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.

Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:

Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:

Значит НОД (24 и 18) = 6

Третий способ нахождения НОД

Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.

Пример 1. Найти НОД чисел 28 и 16.

В первую очередь, раскладываем числа 28 и 16 на простые множители:

Получили два разложения: 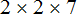и

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:

Теперь перемножаем оставшиеся множители и получаем НОД:

Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:

Пример 2. Найти НОД чисел 100 и 40

Раскладываем на множители число 100

Раскладываем на множители число 40

Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения

Перемножим оставшиеся числа:

Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:

Пример 3. Найти НОД чисел 72 и 128

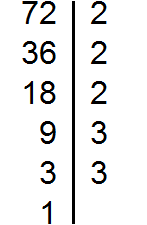
Раскладываем на множители число 72

Раскладываем на множители число 128

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:

Перемножим оставшиеся числа:

Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:

Нахождение НОД для нескольких чисел

Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.

Например, найдём НОД для чисел 18, 24 и 36

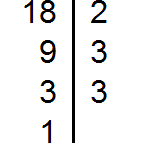
Разложим на множители число 18

Разложим на множители число 24

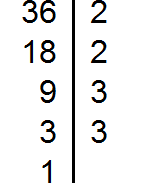
Разложим на множители число 36

Получили три разложения:

Теперь найдём и подчеркнём общие множители:

Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:

Пример 2. Найти НОД для чисел 12, 24, 36 и 42

Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.

Разложим на множители число 12

Разложим на множители число 24

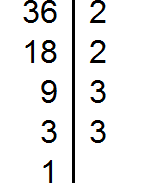
Разложим на множители число 36

Разложим на множители число 42

Получили четыре разложения:

Теперь найдём и подчеркнём общие множители:

Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:

Наименьшее общее кратное

Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.

Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.

Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.

Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:

Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.

Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.

Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.

В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.

Итак, начнём. Кратные будем выделять синим цветом:

Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:

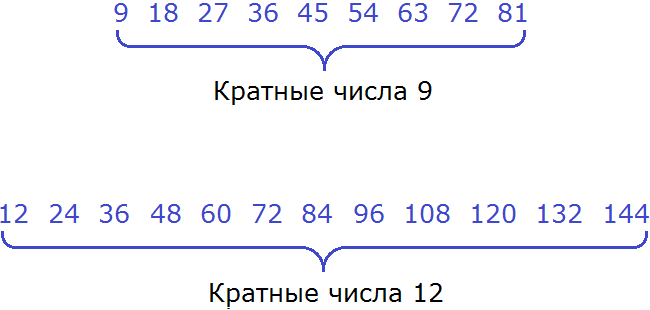
Теперь выпишем кратные обоих чисел:

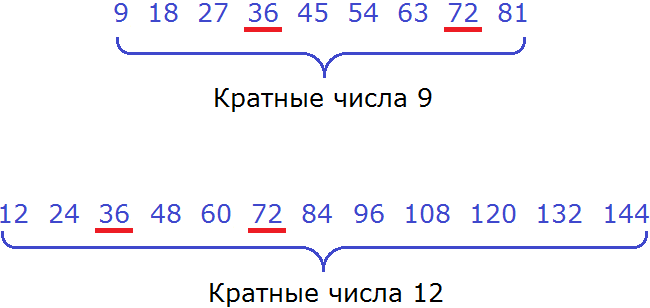
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:

Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.

Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

Второй способ нахождения НОК

Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.

Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.

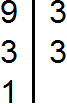
Разложим на множители число 9

Разложим на множители число 12

Выпишем первое разложение:

Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:

Теперь перемножаем эти множители:

Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.

Пример 2. Найти НОК чисел 50 и 180

Разложим на множители число 50

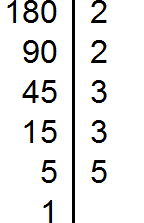
Разложим на множители число 180

Выпишем первое разложение:

Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:

Теперь перемножаем эти множители:

Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:

Пример 3. Найти НОК чисел 8, 15 и 33

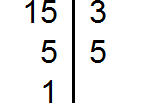
Разложим на множители число 8

Разложим на множители число 15

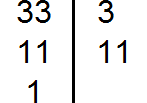
Разложим на множители число 33

Выпишем первое разложение:

Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:

Теперь перемножаем эти множители:

Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:

НОК (8, 15 и 33) = 1320

Третий способ нахождения НОК

Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.

Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.

К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:

Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.

Итак, перемножим числа 24 и 12

Разделим полученное число 288 на НОД чисел 24 и 12

Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24

Пример 2. Найти НОД и НОК чисел 36 и 48

Найдем НОД чисел 36 и 48

Перемножим числа 36 и 48

Разделим 1728 на НОД чисел 36 и 48

Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144

Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144

Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».

Источник