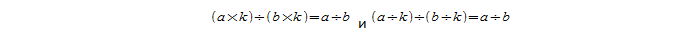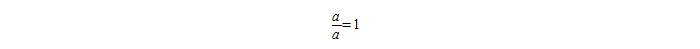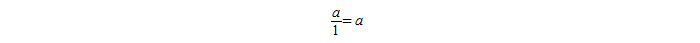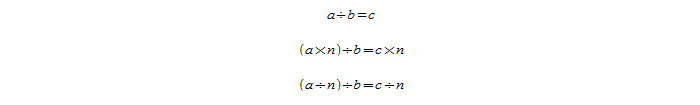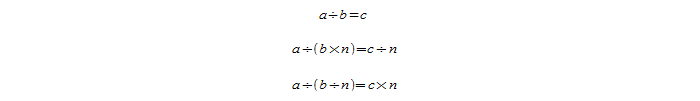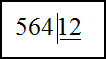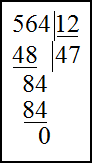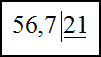Что такое наименьшее частное

Что такое частное в математике?

В каждом разделе научных или практических знаний используются собственные понятия и определения. Они нужны человеку для того, чтобы максимально упростить понимание и применение разных явлений и действий, которые описываются при помощи этих терминов. «Частное» является таким термином, этим словом описывают одну из четырёх простейших операций в математике.

В математической операции деления участвуют несколько чисел, каждому из них присвоено определённое название. «Частным» называют результат деления, другие задействованные в этой операции компоненты обозначают как «делимое» (число, на которое делят), «делитель» (количество единиц деления) и «остаток» (представляет собой произведение дробной части частного на делитель). К примеру, при целочисленном делении числа 34 на 6 к частному будет относиться 5, к делимому – 34, к делителю – 6, а остатком от деления будет являться число 4.

Если в операции присутствует одна или несколько переменных, то частное не всегда будет представлять из себя целое или дробное число, это может быть и просто математическое выражение. В целом, к частному можно отнести всё, что находится после знака равенства в тождестве, где левая часть – это операция деления. К примеру, в случае деления выражения 6*x?+12 на 3, частным будет являться выражение 2*x?+4.

Иногда термин «частное» заменяют обозначением «отношение». Т.е., теоретически, назвав результат деления 34 на 6 любым из данных двух определений, вы будете в обоих случаях правы. Однако всё-таки чаще всего термином «отношение» называют левую часть тождества, иначе говоря, ещё не осуществленную операцию деления, а термин «частное» применяют к правой части, т. е. к полученному результату.

Слово «частное» применяют не только в качестве математического термина, существуют и другие широко используемые понятия, обозначаемые точно также. Нередко это слово употребляют в виде прилагательного для подчёркивания противопоставления – к примеру, «частное мнение». В области юриспруденции слово «частное», по сути, аналогично понятию «негосударственное» – к примеру, «частная собственность».

Вместе со статьёй «Что такое частное в математике?» читают:

Источник

Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.

Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.

Основное свойство частного

Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.

По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.

Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:

10 — 2 — 2 — 2 — 2 — 2 = 0.

Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:

Частное чисел – это итог процесса деления одного значения на второе. Пример:

Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:

При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:

Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:

Увеличение или уменьшение делимого

Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.

Изложенное правило имеет такой вид:

12 ⁄ 2 = 6 и пусть n = 3.

Проведём увеличение и уменьшение делимого:

То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.

Увеличение или уменьшение делителя

Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:

Для примера требуется взять частное двух значений 54 и 6:

a / b = c и пусть n = 3.

Проведём увеличение и уменьшение делителя:

Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.

Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.

Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.

Источник

Что такое частное чисел

Определение частного чисел

Задание. Найти частное чисел:

Для нахождения частного больших чисел или десятичных дробей используют способ деления в столбик.

Что такое частное чисел не по зубам? Тебе ответит эксперт через 10 минут!

Задание. Найти частное чисел:

Решение. Для нахождения частного в первом примере выполним деление в столбик. Для этого запишем делимое и делитель следующим образом

Для нахождения частного во втором примере, сведем деление десятичных дробей к делению десятичной дроби на целое число. Для этого будем передвигать запятую вправо у делимого и делителя до тех пор, пока делимое не станет целым числом. Далее запишем полученные числа в столбик, как и в первом примере:

Частное рациональных дробей находится по правилу

Задание. Найти частное рациональных дробей:

Решение. 1) Воспользуемся правилом вычисления частного рациональных дробей:

Для вычисления частного во втором примере, сначала запишем дроби в виде неправильных дробей. Для этого целую часть умножим на знаменатель и прибавим к числителю. Затем применим правило вычисления частного рациональных дробей:

Источник

Деление натуральных чисел

Подобно тому, как вычитание является обратным действием для сложения, так и для умножения существует свое обратное арифметическое действие.

Рассмотрим задачу. В школьной столовой раздали 90 яблок по 3 яблока каждому ученику класса. Сколько учеников учатся в этом классе?

Если бы нам было известно количество учеников в классе и количество яблок, которое получил каждый из них, то общее число яблок мы узнали бы, умножив число учеников на число яблок, доставшееся каждому. То есть, количество учеников – это первый сомножитель, количество яблок – второй сомножитель, а сколько яблок раздали – это произведение.

Деление – это арифметическое действие, которое состоит в нахождении одного из сомножителей при помощи данного произведения и второго сомножителя.

Делимое – это число, которое мы делим на другое. Это то самое произведение, которое нам дано.

Делитель – это число, на которое мы делим делимое. Это данный нам один из множителей.

Частное – это результат действия деление, то есть, искомый нами второй сомножитель.

На записи действие деление обозначается: двоеточием ( \(\textcolor <:>\) ), знаком обелюс ( \(\textcolor <\div>\) ), горизонтальной чертой или косой чертой ( \(\textcolor \) ).

Так, решение нашей задачи можно записать следующими способами:

При записи от руки действие деление принято записывать в виде двоеточия, обелюс применяется в печатной литературе, косая черта, которая по-другому называется слеш, – при записи на компьютере, а горизонтальная черта используется при записи деления в виде обыкновенной дроби.

Итак, разделить число a на число b – это значит найти такое число c, которое при умножении его на число b дает в результате числа a.
То есть: \(\textcolor \) , если \(\textcolor \) .

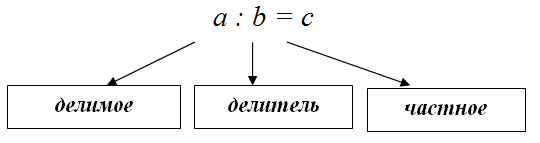
Компоненты действия деление:

Деление с остатком и неполное частное

К примеру, если мы захотим раздать все 37 яблок поровну между пятью детьми, то у нас это сделать не получится. Мы сможем раздать (использовать из всего количества яблок) только по 7 яблок каждому ( \(\textcolor <7\cdot 5=35>\) ), и у нас останется 2 яблока ( \(\textcolor <37-35=2>\) ).

Итак, деление с остатком – это нахождение такого наибольшего целого числа, умножив которое на делитель, мы получим число, максимально близкое к делимому, но не превосходящее его. Это искомое число называется неполное частное. Разница между делимым и неполным частным называется остаток.

Остаток всегда меньше делителя!

Связь деления с умножением, сложением и вычитанием

Когда мы выполняем находим произведение двух чисел, эти числа нам известны, а от нас требуется найти результат действия умножение. При делении (без остатка) нам известно произведение двух чисел, а найти нужно такое число, которое при умножении на известное данное число дает это самое произведение.

Следовательно, действие деление является обратным действию умножения.

Справедливо также и обратное, что действие умножение обратно действию деления. Таким образом:

Умножение и деление – это взаимно обратные действия.

Связь деления с умножением, а также со сложением и вычитанием прекрасно видна, если рассмотреть, как с помощью этих действий можно выполнить действие деление.

Деление двух чисел при помощи сложения

Деление двух чисел при помощи вычитания

То есть, 69 от 345 можно отнять 5 раз, поэтому \(\textcolor <349\div 69=5>\).

Деление двух чисел при помощи умножения

При помощи умножения узнать ответ на наш вопрос можно перебирая множитель числа 69 до тех пор, пока не получим заданное нам 345 :

Но эти три способа очень громоздки, особенно если частное представляет собой очень большое число. Их нужно знать только для того, чтобы понимать суть действия деления, суть тех задач, которые решаются посредством него.

Общий принцип деления в столбик

Если частное от деления двух чисел является многозначным числом, нахождение его происходит путем деления в столбик. Еще его называют деление уголком.

Прежде всего, нужно узнать количество цифр в частном и первое неполное делимое; как их находить, я подробно расписал в этой статье. В нашем случае первое неполное делимое равно 295 тысяч, а в частном будет 4 цифры.

Далее записываем известные компоненты деления следующим образом:

и начинаем вычисление:

1. Берем первое неполное делимое и пытаемся его разделить на делитель.

Вот тут нам и пригодится способ нахождения однозначного частного. Воспользовавшись им, находим, что в 295 тысячах делитель 34 содержится целиком 8 тысяч раз.

Записываем в частное первую найденную цифру разряда тысяч, а под неполным делимым пишем результат произведения неполного частного и делителя. И сразу же находим остаток от этого действия, т.е. вычитаем из неполного частного результат этого произведения.

В результате умножения первой найденной цифры частного на делитель у нас получилось \(\textcolor <8\cdot 37=272>\). Записываем его под 295 и находим разницу: \(\textcolor <295-272=23>\). Значит, 23 тысячи у нас остаются неразделенными.

В качестве еще одного действия самопроверки нужно сравнить полученную разницу с делителем. Если она меньше делителя, то мы на правильном пути, если же разница равна или больше делителя, то мы или неправильно нашли цифру частного, или допустили ошибку при умножении на делитель либо при нахождении остатка.

2. Оставшиеся неразделенные 23 тысячи представляют собой 230 сотен. Прибавляем к ним те 3 сотни, которые содержатся в делимом (говорят: сносим пять) и получаем второе неполное делимое 233 сотни.

3. 29 неразделенных сотен – это 290 десятков. Добавляем (сносим) к ним 8 десятков делимого, получаем третье неполное делимое 298 десятков.

4. И наконец, 26 десятков – это 260 простых единиц. Добавляем (сносим) к ним 3 единицы делимого и получаем четвертое неполное делимое 263 единицы.

Рассмотрим еще один пример. \(\textcolor <25326\div 63>\).

1 сотня = 10 десятков, добавляем (сносим) 2 десятка из делимого, получаем второе неполное делимое 12 десятков.

Итак, запомните, что каждое неполное делимое образует в частном одну цифру соответствующего разряда и что даже если неполное делимое меньше делителя, то в частном все равно нужно записать нулевой результат этого действия.

Итак, в общем виде алгоритм деления в столбик выглядит так:
1. Находим первое неполное делимое и количество цифр в частном.
2. Делим неполное делимое на делитель. Цифру, полученную в результате деления записываем ниже черты под делителем.
3. Умножаем полученную цифру на делитель, результат записываем под неполным делимым.
4. Ставим между ними знак минус и выполняем действие.
5. К полученной разнице сносим цифру следующего разряда (если она есть) и получаем второе неполное делимое.
6. Выполняем пункты 2-5 до тех пор, пока в делимом не останется ни одной неснесенной цифры.
7. Если неполное делимое невозможно разделить на делитель, то в частном ставится 0 и к этому неполному делимому сносится следующая цифра.

Деление на числа, заканчивающиеся нулями

Как и в случае с умножением, деление чисел облегчается, если делитель заканчивается одним или несколькими нулями. Рассмотрим два возможных случая:

Рассмотрим первый случай.

Деление на единицу с любым количеством нулей

Единица с любым количеством нулей – это не что иное как единица соответствующего разряда. Например, 10 – это 1 единица разряда десятков, 1000 – это одна единица разряда тысяч, 10000000 – 1 единица разряда десятков миллионов и т.д.

Запишите:
Чтобы разделить какое-нибудь число на единицу с любым количеством нулей, нужно отсчитать в делимом справа столько цифр, сколько нулей содержится в делителе; тогда все цифры, находящиеся слева от разделения, составят частное, а те, что справа – будут остатком.

Деление на число, оканчивающееся нулями

Рассмотрим на примере \(\textcolor <284556\div 2800>\).

Делитель здесь не что иное как 28 сотен. Логично предположить, что эти 28 сотен могут хотя бы один раз содержаться только в сотнях делимого. Значит, нам нужно определить, сколько в делимом всего единиц разряда сотен, и разделить их на 28 единиц разряда сотен делимого. А отброшенные цифры десятков и простых единиц добавятся к остатку.

Запишите:
Чтобы разделить какое-нибудь число на число, заканчивающееся нулями, нужно отбросить мысленно нули в делителе, в делимом тоже отбросить мысленно такое же количество цифр, как и нулей в делителе. Получившееся число в делимом разделить на получившееся число в делителе, а к остатку прибавить (снести) те цифры делимого, которые отбросили ранее.

Проверка деления

Так как делимое – это делитель, умноженный на частное и плюс остаток, что следует из определения деления, то результат выполнения деления можно проверить умножением.

Если в результате действия деления не получилось остатка, то деление можно проверить и делением. Действительно, если делимое – это произведение делителя и частного, то разделив делимое на частное (один из сомножителей), мы должны получить второй сомножитель, то есть, делитель.

Свойства деления

Свойства деления я представлю двумя группами:

Давайте рассмотрим каждую группу подробнее.

Действия деления с единицей и нулем

При делении числа на единицу получается то же самое число.

Действительно, разделить число на единицу означает узнать, сколько единиц содержится в данном числе. А количество единиц в числе – это не что иное, как само это число.

И ли вот, например, если 10 яблок нужно раздать одному человеку ( 10 поделить на 1 ), то ему все эти 10 яблок и достанутся, правда?

При деление одинаковых чисел (числа на равное число) в результате будет 1 (единица).

В самом деле, если все единицы какого-то числа разделить на количество частей, равное количеству единиц этого числа, то в каждая часть получит по 1 единице.

Например, если 20 яблок раздать 20 школьникам, то каждому достанется по 1 яблоку.

При делении нуля на любое число, отличное от нуля, в результате будет нуль.

Разделить нуль на число означает найти такое число, умножив которое на данный делитель, мы получим в результате нуль. А такое число только одно – это нуль.

На нуль делить нельзя, то есть, нуль не может выступать в роли делителя.

При делении каких угодно чисел делителем может быть любое число, кроме нуля.

Рассмотрим два случая: когда нулём является только делитель, и когда делимое и делитель оба нули.

Распределительные свойства деления

Чтобы найти частное от деления суммы на число, нужно поделить каждое слагаемое на это число, и найти сумму полученных частных.
\(\textcolor <(a+b+c)\div d=a\div d+b\div d+c\div d>\).
При этом подразумевается, что все действия деления получаются без остатка.

Чтобы найти частное от деления разности на число, нужно поделить на это число отдельно сперва уменьшаемое, а потом вычитаемое, после чего найти разность первого частного и второго.
\(\textcolor <(a-b)\div c=a\div c-b\div c>\)
При этом также предполагается, что при делениях уменьшаемого и вычитаемого на число не получается остатков.

Например: \[\textcolor <(36-24)\div 6=36\div 6-24\div 6=6-4=2>\] Число 36 состоит из 6 шестерок, а 24 – из 4 шестерок, а забрав у 6 шестерок 4 шестерки, получим 2 шестерки. Такой же итог будет и если мы сперва у 36 отнимем 24 единицы (останется 12 ), а потом найдем, сколько в этой разнице содержится шестерок: \(\textcolor <12\div 6=2>\).

Чтобы найти частное от деления произведения на число, нужно поделить на него только один из сомножителей, а результат умножить на неизмененные остальные.
\(\textcolor <(a\cdot b\cdot c)\div d=a\div d\cdot b\cdot c=b\div d\cdot a\cdot c=c\div d\cdot a\cdot b>\).

Чтобы найти частное от деления числа на произведение, нужно это число поделить на первый сомножитель, результат деления поделить на второй сомножитель, полученное частное – на третий и так далее.
\(\textcolor \).
При этом предполагается, что при всех этих делениях не получается остатков.

На рисунке наглядно видно, что в итоге после применения этого правила, число 30 получилось разделенным на 6 равных частей.

Изменение частного при изменении делимого и делителя

При рассмотрении изменений частного в результате изменений делимого и делителя предполагается, что действие деление происходит без остатка. В противном случае изменения могут быть не такими, о которых идет речь ниже.

При увеличении делимого в определенное количество раз, частное увеличится в это же количество раз, а при уменьшении – уменьшится.

Если мы в примере \(\textcolor <24\div 4=6>\) делимое увеличим, к примеру, в 3 раза, то мы можем переписать это выражение в виде \(\textcolor <(24+24+24)\div 4>\). Используя свойство деления суммы на число, мы увидим, что теперь нам нужно сложить три слагаемых, каждое из которых равно начальному выражению: \(\textcolor <24\div 4+24\div 4+24\div4>\). Отсюда очевидно, что результат будет больше начального в 3 раза.

Если мы в этом же примере \(\textcolor <24\div 6>\) уменьшим делимое в 3 раза, то есть, разделим его на три равные части, то очевидно, что результат деления одной части на 6 будет в 3 раза меньше, чем результат деления трех таких же частей. Посмотрите сами. Начальное выражение \(\textcolor <24\div 6>\) можно записать в виде: \(\textcolor <(8+8+8)\div 6=8\div 6+8\div 6+8\div 6>\), а уменьшенное в 3 раза делимое даст нам только одно из трех таких слагаемых: \(\textcolor <8\div 6>\).

При увеличении делителя в определенное количество раз, частное уменьшится в это же количество раз, а при уменьшении – увеличится.

Действительно, изменение делителя означает, что делимое необходимо разделить на большее или меньшее количество равных частей. Соответственно, если нужно разделить на большее число частей, то каждая часть будет меньше, чем изначально, а если делить на меньшее число частей, то каждая часть будет крупнее.

В случае одновременного изменения делимого и делителя, частное может вести себя по-разному, или же вообще оставаться без изменений. Если нужно узнать, станет оно больше или меньше, нужно сперва посмотреть, как частное изменится после изменения делимого, а потом – как изменится после изменения делителя.

При увеличении или уменьшении делимого и делителя в одинаковое количество раз, частное не меняется.

Попробуйте самостоятельно доказать справедливость этого утверждения. Пишите в комментариях, получилось это, или нет.

Источник

Что такое частное в математике?

Математика – уникальная наука, которая привлекает точностью и последовательностью. Каждый, кто начал изучать эту важную дисциплину, должен разобраться, что такое частное в математике.

Деление

В математике есть четыре простейших операции:

Если мы говорим о частном, то нас будет интересовать такая операция, как деление.

Деление всегда обратно умножению. Это математическая величина, которую мы получим, разделив одно число на другое. Есть ряд символов, которые обозначают его:

В учебных пособиях для учеников 1 – 5 классов есть простое и точное определение этого понятия. Деление – это операция, в результате которой мы получаем число, которое при умножении на делитель дает делимое. Число, о котором говорится в первой части определения, и есть частное.

Частное рассказывает, во сколько раз одно число больше другого.

Наглядные примеры

Чтобы лучше понять, что такое частное чисел в математике, следует обратиться к примерам. Они помогут разложить знания по полочкам в вашей голове. Решение примеров – это лучший тренажер для усвоения новых знаний. Приступим к их решению.

Итак, частное получается, если делимое поделить на делитель. При помощи символов эту операцию можно записать следующим образом:

Запишем простой пример из математики:

80:2=40

80 – делимое (оно делится)

2 – это делитель (на него разделяют)

Восемьдесят больше, чем сорок, в два раза.

Другой пример выглядит так:

120:2=60

Сто двадцать больше, чем шестьдесят, в два раза.

Проверка

Если вы провели операцию деления и сомневаетесь в результате, на помощь придет проверка. Для этого умножьте делитель на частное. Если в результате вы получили делимое, то пример решен верно:

Если после знака равно вы увидели знакомое вам делимое, то можете поставить себе твердую пятерку. Вы научились находить частное чисел и делать проверку. Это очень важно, чтобы в дальнейшем освоить более сложные понятия в алгебре и геометрии.

Частное – это основа математики. Если ученик не смог понять его суть, то двигаться дальше просто бессмысленно. Обратитесь к учителю, если это понятие так и осталось для вас туманным. Педагог разъяснит все ошибки и укажет на подводные камни.

Полное и неполное частное

В результате проведения математических подсчетов частное может быть двух видов:

100:2=50

50 – полное частное

51:2=25 (остаток 1)

25 – неполное частное

1 – остаток от деления

Если вы откроете учебник математики, то увидите, что частное в задачах обозначают при помощи различных символов (переменных). Для этого используют латинские буквы:

30:6=x

Чтобы найти частное, следует делимое разделить на делитель:

Ответ 5 – это частное в данном примере.

Абстрактные определения и туманные рассуждения плохо усваиваются мозгом школьника. Поэтому всегда держите под рукой задачник со списком упражнений по математике. Он поможет понять различные математические категории на практике. Конкретные цифры, записанные в тетради, станут главными помощниками.

Источник