Что такое наименьшее число в математике
Изучение точного предмета: натуральные числа это какие числа, примеры и свойства
В математике существует несколько различных множеств чисел: действительные, комплексные, целые, рациональные, иррациональные, дробные… В нашей повседневной жизни мы чаще всего используем натуральные числа, так как мы сталкиваемся с ними при счете и при поиске, обозначении количества предметов….
Какие числа называются натуральными
Из десяти цифр можно записать абсолютно любую существующую сумму классов и разрядов. Натуральными значениями считаются те, которые используются:
N значения всегда целые и положительные. Наибольшего N не существует, так как множество целых значений не ограничено.
Внимание! Натуральные числа получаются при счете предметов или при обозначении их количества.
Абсолютно любое число может быть разложено и представлено в виде разрядных слагаемых, например: 8.346.809=8 миллионов+346 тысяч+809 единиц.
Множество N
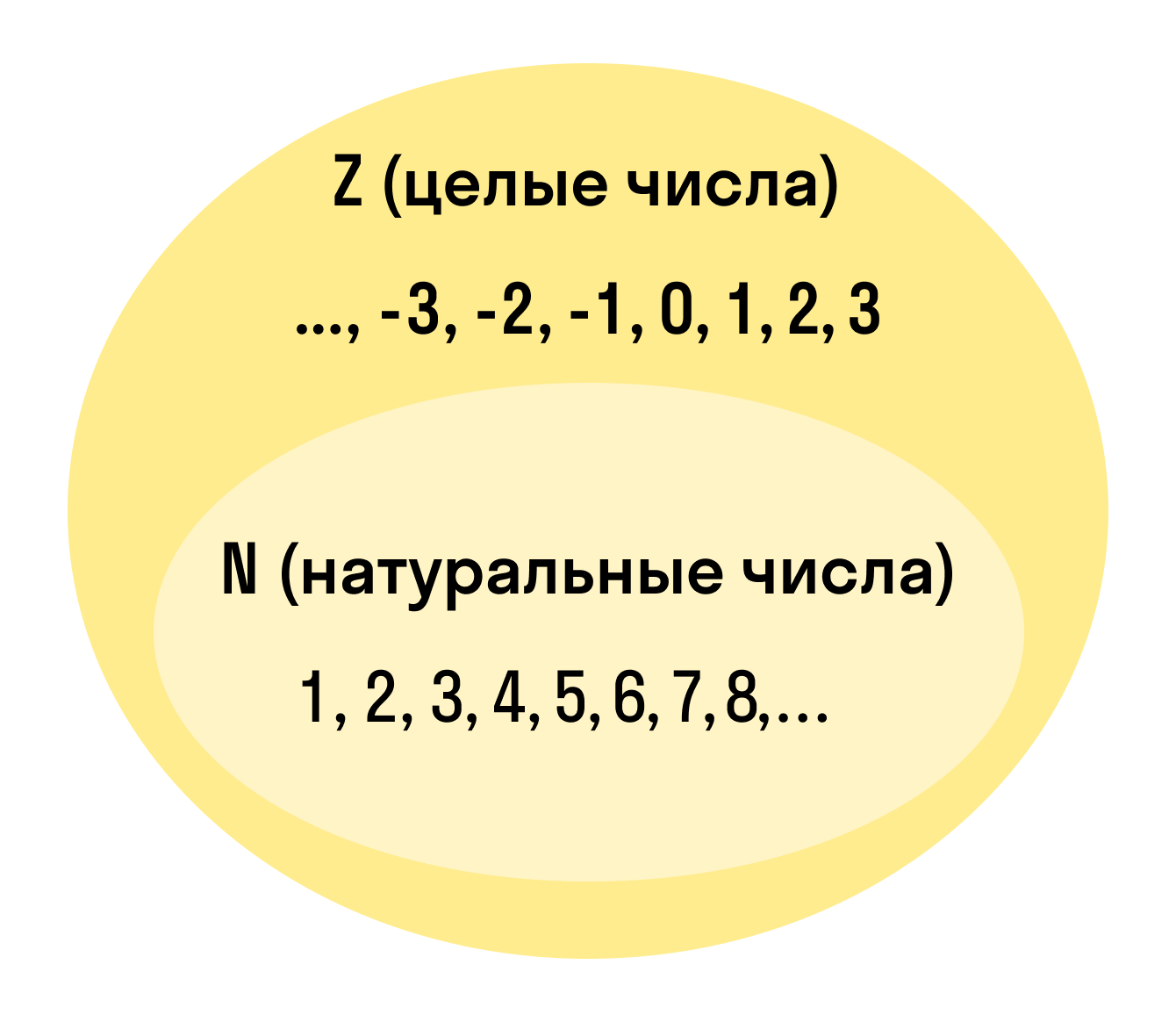
Множество N находится в множестве действительных, целых и положительных. На схеме множеств они бы находились друг в друге, так как множество натуральных является их частью.
Множество натуральных чисел обозначается буквой N. Это множество имеет начало, но не имеет конца.
Еще существует расширенное множество N, где включается нуль.
Наименьшее натуральное число
Но в иностранных математических школах, например во французской, нуль считается натуральным. Наличие в ряде нуля облегчает доказательство некоторых теорем.
Ряд значений N, включающий в себя нуль, называется расширенным и обозначается символом N0 (нулевой индекс).
Ряд натуральных чисел
N ряд – это последовательность всех N совокупностей цифр. Эта последовательность не имеет конца.
Особенность натурального ряда заключается в том, что последующее число будет отличаться на единицу от предыдущего, то есть возрастать. Но значения не могут быть отрицательными.
Внимание! Для удобства счета существуют классы и разряды:
Все N
Все N находятся во множестве действительных, целых, неотрицательных значений. Они являются их составной частью.
Эти значения уходят в бесконечность, они могут принадлежать классам миллионов, миллиардов, квинтиллионов и т.д.
Например:
Последовательность в N

от нуля до плюс бесконечности, включая концы, и от единицы до плюс бесконечности, включая концы, то есть все положительные целые ответы.
N совокупности цифр могут быть как четными, так и не четными. Рассмотрим понятие нечетности.
Нечетные (любые нечетные оканчиваются на цифры 1, 3, 5, 7, 9.) при делении на два имеют остаток. Например, 7:2=3,5, 11:2=5,5, 23:2=11,5.
Что значит четные N
Любые четные суммы классов оканчиваются на цифры: 0, 2, 4, 6, 8. При делении четных N на 2, остатка не будет, то есть в результате получается целый ответ. Например, 50:2=25, 100:2=50, 3456:2=1728.
Важно! Числовой ряд из N не может состоять только из четных или нечетных значений, так как они должны чередоваться: за четным всегда идет нечетное, за ним снова четное и т.д.
Свойства N
Как и все другие множества, N обладают своими собственными, особыми свойствами. Рассмотрим свойства N ряда (не расширенного).
Внимание! Все вышеперечисленные неравенства действительны и в обратном направлении.
Как называются компоненты умножения

Для того, чтобы быстро и правильно умножать и уметь решать обратные задачи, необходимо знать компоненты умножения.
15.10=150. В данном выражении 15 и 10 являются множителями, а 150 – произведением.
Умножение обладает свойствами, которые необходимы при решении задач, уравнений и неравенств:
Например: 15.Х=150. Разделим произведение на известный множитель. 150:15=10. Сделаем проверку. 15.10=150. По такому принципу решаются даже сложные линейные уравнения (если упростить их).
Важно! Произведение может состоять не только из двух множителей. Например: 840=2.5.7.3.4
Что такое натуральные числа в математике?
Разряды и классы натуральных чисел
Вывод
Подведем итоги. N используются при счете или обозначении количества предметов. Ряд натуральных совокупностей цифр бесконечен, но он включает в себя только целые и положительные суммы разрядов и классов. Умножение тоже необходимо для того, чтобы считать предметы, а также для решения задач, уравнений и различных неравенств.
Это интересно! Легкие правила округления чисел после запятой
Разряды и классы чисел
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Числа и цифры
Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.
Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.
Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определенное место — позицию.
Классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.
Названия классов многозначных чисел справа налево:
Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
А теперь прочитаем число единиц каждого класса слева направо:
Разряды чисел
От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.
Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще чтобы визуально разделить классы чисел.
Разрядные единицы обозначают так:
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Чтобы легче понимать математику — записывайтесь на наши курсы по математике!
Потренируемся
Пример 1. Записать цифрами число, в котором содержится:
Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.
Пример 2. Сколько сотен содержится в числе 6284?
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.
Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.
Значит, в данном числе содержится 62 сотни.
Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.
Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.
Натуральные числа
Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и т. д.
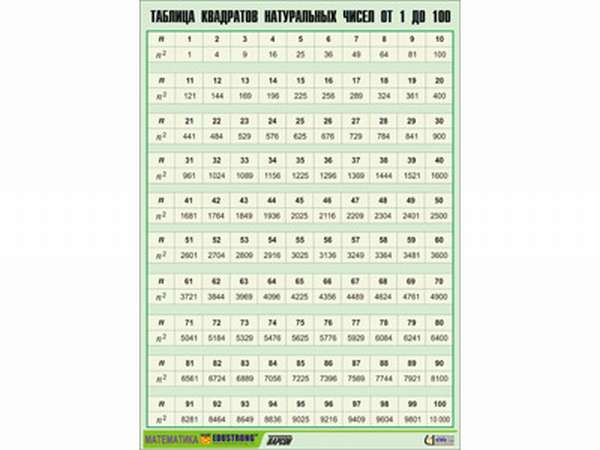
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
Какие операции возможны над натуральными числами
Записывайтесь на курсы обучения математике для учеников с 1 по 11 классы!
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это примеры неправильной записи натуральных чисел, потому что ноль расположен слева. Число не может начинаться с нуля. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двузначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа самого на себя | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 × 8) |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами:
Урок 9 Бесплатно Меньше или больше
Вы уже знаете, что такое натуральное число и как оно записывается.
Также Вам известно, что такое координатный луч.
Сегодня мы применим эти знания, чтобы сформулировать понятия “больше” и “меньше” для натуральных чисел, научимся отвечать на вопрос, как соотносятся два натуральных числа.
Узнаем, как сравнивать числа с помощью координатного луча, как сравнивать натуральные числа с одинаковым и разным количеством знаков, разберем понятие “сортировка” для чисел.
Определение
Вспомним, как выглядит натуральный ряд:
1, 2, 3, 4, 5, 6, 7, 8, 9 …
Из двух натуральных чисел больше то, которое при счете называют позже.
Из двух натуральных чисел меньше то, которое при счете называют раньше.
Данное определение достаточно просто и понятно, посмотрим на примерах.
Например, как соотносятся 3 и 5?
Если мы посмотрим на натуральный ряд, то увидим, что 3 названо раньше, чем 5, следовательно, 3 меньше 5-ти.
Другой пример, как соотносятся числа 9 и 6?
Опять же, надо посмотреть на натуральный ряд, тогда можно увидеть, что 9 названо позже, чем 6, значит, 9 больше 6-ти.
Каждый раз писать словами “больше” или “меньше” может быть неудобно, поэтому удобно использовать знаки.
Знак “ ” читается как “больше”.
Таким образом, чтобы кратко записать, что 3 меньше 5-ти, достаточно написать “\(\mathbf<3 6>\)”.
Запись с использование знаком “больше” или “меньше” называют неравенством.
Довольно часто вопрос про соотношение двух чисел может ставится так: “какой знак должен стоять в неравенстве на месте пропуска”, а дальше идет неравенство с пропущенным знаком, например, такое: “4 _ 6”.
В данном случае надо ответить на вопрос, больше ли 4 6-ти или меньше, и поставить соответствующий знак.
Здесь первое число меньше второго и нужно поставить знак “ 0”, “2 > 0”, “3 > 0” и так далее для каждого натурального числа.
Пройти тест и получить оценку можно после входа или регистрации
Какие числа называются целыми
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение целых чисел
Что важно знать о целых числах:
Целые числа на числовой оси выглядят так:
На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.
В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и отрицательные числа. Множество целых чисел обозначают Z.
Выглядит эти ребята вот так:
Последовательность целых чисел можно записать так:
Свойства целых чисел
Таблица содержит основные свойства сложения и умножения для любых целых a, b и c: