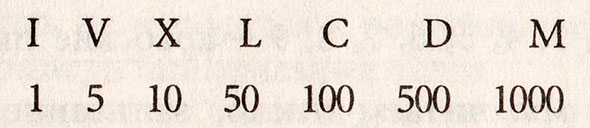Что такое натуральное значение в математике 6 класс
Натуральные числа
Натуральные числа — одно из старейших математических понятий.
В далёком прошлом люди не знали чисел и, когда им требовалось пересчитать предметы (животных, рыбу и т.д.), они делали это не так, как мы сейчас.
Количество предметов сравнивали с частями тела, например, с пальцами на руке и говорили: «У меня столько же орехов, сколько пальцев на руке».
Со временем люди поняли, что пять орехов, пять коз и пять зайцев обладают общим свойством — их количество равно пяти.
Наибольшего натурального числа не существует.
При счёте число ноль не используется. Поэтому ноль не считается натуральным числом.
Затем появились и особые знаки для обозначения чисел — предшественники современных цифр. Цифры, которыми мы пользуемся для записи чисел, родились в Индии примерно 1 500 лет назад. В Европу их привезли арабы, поэтому их называют арабскими цифрами.
Натуральный ряд — это последовательность всех натуральных чисел:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …
Натуральный ряд бесконечен, наибольшего натурального числа в нём не существует.
Десятичной потому, что 10 единиц каждого разряда образуют 1 единицу старшего разряда. Позиционной потому, что значение цифры зависит от её места в записи числа, то есть от разряда, в котором она записана.
Разряды и классы (включая класс миллионов) подробно разобраны на нашем сайте в материалах для начальной школы.
Класс миллиардов
Если взять десять сотен миллионов, то получим новую разрядную единицу — один миллиард или в записи цифрами.
1 000 миллионов = 1 000 000 000 = 1 млрд
Десять таких единиц — десять миллиардов, десять десятков миллиардов образуют следующую единицу — сто миллиардов.
Миллиарды, десятки миллиардов и сотни миллиардов образуют четвёртый класс — класс миллиардов.
Разряды и классы натурального числа
Рассмотрим натуральное число 783 502 197 048
| Название класса | Миллиарды | Миллионы | Тысячи | Единицы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Название разряда | Сотни миллиардов | Десятки миллиардов | Миллиарды | Сотни миллионов | Десятки миллионов | Миллионы | Сотни тысяч | Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
| Цифра (символ) | 7 | 8 | 3 | 5 | 0 | 2 | 1 | 9 | 7 | 0 | 4 | 8 |
| Название класса | Миллиарды | Миллионы | Тысячи | Единицы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Название разряда | Сотни миллиардов | Десятки миллиардов | Миллиарды | Сотни миллионов | Десятки миллионов | Миллионы | Сотни тысяч | Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
| Цифра (символ) | 7 | 8 | 3 | 5 | 0 | 2 | 1 | 9 | 7 | 0 | 4 | 8 |
C помощью таблицы разрядов прочитаем это число. Для этого надо слева направо по очереди называть количество единиц каждого класса и добавлять название класса.
Название класса единиц не произносят, также не произносят название класса, если все три цифры в его разрядах — нули.
Любое натуральное число можно записать в виде разрядных слагаемых.
Числа 1, 10, 100, 1000 … называются разрядными единицами. С их помощью натуральное число записывается в виде разрядных слагаемых. Так, например, число 307 898 будет выглядеть в виде разрядных слагаемых.
307 898 = 300 000 + 7 000 + 800 + 90 + 8
Проверить свои вычисления вы можете с помощью нашего калькулятора разложения числа на разряды онлайн.
Следующие за миллиардом классы названы в соответствии с латинскими наименованиями чисел. Каждая следующая единица содержит тысячу предыдущих.
Все числа пересчитать невозможно, поскольку за каждым числом следует число на единицу большее, но очень большие числа в повседневной жизни не нужны.
Однако, физики нашли число, которое превосходит количество всех атомов (мельчайших частиц вещества) во всей Вселенной.
Это число получило специальное название — гугол. Гугол — число, у которого 100 нулей.
Что такое Натуральное число
Определение натурального числа
Натуральные числа — это те числа, которые появились натуральным способом, когда считали сколько у человека есть предметов. Например: 1, 2, 3, 4, 5 и т. д.
Наибольшее натуральное число: не существует. Наименьшее натуральное число: 1.
Например, люди считали, сколько у них было фруктов: 1 яблоко, 3 апельсина, 2 дыни.
Нуль (0) не является натуральным числом, хотя некоторые области математики всё-таки считают 0 натуральным числом.
Отрицательные числа (–1, –3, –5. ) не являются натуральными числами («–3» яблок сложно посчитать физически).
Дроби (например, ⅓ или ⅖) тоже не являются натуральными числами.
Такие понятия, как отрицательные («–3»), дроби («⅓») и нуль («0») появились много позже.
Множество натуральных чисел
Множество натуральных чисел бесконечно и обозначается буквой N, т. е.:
Натуральные числа:
Натуральные числа с нулём:
Ряд натуральных чисел
Если записать все натуральные числа в порядке возрастания (каждое натуральное число отличается от предыдущего на 1), это будет ряд натуральных чисел. Но если какие-то числа будут отсутствовать, это уже не будет считаться рядом натуральных чисел. Например:
Наибольшего натурального числа не существует — натуральный ряд бесконечен.
Ненатуральные числа
Ненатуральные числа — это отрицательные и нецелые числа (обычно 0 тоже считается ненатуральным, но не всегда).
Отрицательные числа — это все те, которые ниже нуля, например: –1, –2, –3, –4, –5 и др.;
Свойства натуральных чисел
Натуральные числа обладают следующими свойствами:
Натуральные числа: что такое натуральное число в математике
Содержание:
В математике существует несколько видов чисел. Одними из самых известных и широко применяемых как профессиональными математиками, так и обычными людьми являются натуральные.
Определение
Натуральные числа – это те, которые принято использовать при обычном подсчете каких-либо материальных предметов, событий и вообще всего, что может быть воспринято органами чувств человека. С этим понятием мы сталкиваемся с детства, потому что этот вид чисел наиболее широко используется в обычной жизни. Люди не обращают внимание на то, как часто им приходится использовать натуральный ряд. Вот наглядный пример. Вряд ли кто задает себе вопрос: что такое натуральное число в математике, глядя на обычные часы, по которым мы определяем какое количество часов и минут прошло с момента начала текущих суток. Основная задача, которую выполняют такие числа, заключается в указании количества чего-либо.
Ряд натуральных чисел
Теперь, когда мы усвоили, что значит натуральное число, поговорим о конкретных примерах. Натуральный ряд начинается с числа 1, а для его обозначения используется буква N. Сам ряд представляет собой числовую последовательность, в которой каждое следующее число больше предыдущего на одну единицу.
Другими словами, натуральные числа — это хорошо знакомая нам последовательность. И какие числа в нее входят понять несложно, вот примеры таких чисел:
2, 31, 55, 74, 153, 1507.
А вот ряд, который образуют числа от 1 до 9:
Поговорим про ноль
Относится ли 0 к натуральным числам? Прежде чем ответить на этот вопрос, вернемся к началу нашего изложения и вспомним, что значит натуральное число в математике. При обычном подсчете число 0 не применяют. Ведь он означает отсутствие чего-либо. Когда приходится констатировать факт, что мы чего-то не обнаружили, то никогда не употребляем словосочетания типа: 0 автомобилей или 0 бутылок. Вместо этого более привычной будет следующая фраза: «нет ни одной бутылки». Исходя из этого ответ на вопрос: входит ли 0 в натуральные числа, отпадает сам по себе. Однозначно, таковым его называть нельзя.
О самом большом числе
Как долго продолжается натуральный ряд? Числа в нем могут быть как одно- и двухзначными, так и трех-, четырехзначными и больше. Поэтому самое большое натуральное число в математике отсутствует, а ряд считают бесконечным.
Натуральные числа с нолями
С одной стороны, мы выяснили, что 0 не относится к натуральным числам. Но вполне естественно выглядит вопрос: 10 – натуральное число или нет? Безусловно, это число и любое другое с неограниченным количеством нолей относят к этому виду, потому что они могут применяться при подсчете или перечислении.
Действия, которые могут выполняться над натуральными числами
Над натуральными числами можно выполнять различные математические операции.
Также существует степень натурального числа, а запись выглядит следующим образом: ab, где: а – основание степени, а b – показатель. Например, 3 2 = 9.
Разряды и натуральные числа
Разрядом называют место нахождения цифры в числе. Каждый разряд называется индивидуально, они располагаются по старшинству – справа налево и от младшего к старшему. Количество цифр числа совпадает с количеством разрядов.
Самым низшим из разрядов являются единицы, а самый старший всегда соответствует крайней левой цифре.
Например, число 5 469 содержит четыре разряда:
Более высокие разряды называют:
Разряды объединяют в классы, каждый из которых включает три разряда:
Между классами для удобства чтения принято делать пробел.
Что такое натуральные значения в математике? Это любые значения, выраженные с использованием чисел натурального ряда. Еще один пример: 184 345 567 100 – в этом числе четыре класса: единицы, тысячи, миллионы и миллиарды.
Изучение точного предмета: натуральные числа это какие числа, примеры и свойства
В математике существует несколько различных множеств чисел: действительные, комплексные, целые, рациональные, иррациональные, дробные… В нашей повседневной жизни мы чаще всего используем натуральные числа, так как мы сталкиваемся с ними при счете и при поиске, обозначении количества предметов….
Какие числа называются натуральными
Из десяти цифр можно записать абсолютно любую существующую сумму классов и разрядов. Натуральными значениями считаются те, которые используются:
N значения всегда целые и положительные. Наибольшего N не существует, так как множество целых значений не ограничено.
Внимание! Натуральные числа получаются при счете предметов или при обозначении их количества.
Абсолютно любое число может быть разложено и представлено в виде разрядных слагаемых, например: 8.346.809=8 миллионов+346 тысяч+809 единиц.
Множество N
Множество N находится в множестве действительных, целых и положительных. На схеме множеств они бы находились друг в друге, так как множество натуральных является их частью.
Множество натуральных чисел обозначается буквой N. Это множество имеет начало, но не имеет конца.
Еще существует расширенное множество N, где включается нуль.
Наименьшее натуральное число
Но в иностранных математических школах, например во французской, нуль считается натуральным. Наличие в ряде нуля облегчает доказательство некоторых теорем.
Ряд значений N, включающий в себя нуль, называется расширенным и обозначается символом N0 (нулевой индекс).
Ряд натуральных чисел
N ряд – это последовательность всех N совокупностей цифр. Эта последовательность не имеет конца.
Особенность натурального ряда заключается в том, что последующее число будет отличаться на единицу от предыдущего, то есть возрастать. Но значения не могут быть отрицательными.
Внимание! Для удобства счета существуют классы и разряды:
Все N
Все N находятся во множестве действительных, целых, неотрицательных значений. Они являются их составной частью.
Эти значения уходят в бесконечность, они могут принадлежать классам миллионов, миллиардов, квинтиллионов и т.д.
Например:
Последовательность в N

от нуля до плюс бесконечности, включая концы, и от единицы до плюс бесконечности, включая концы, то есть все положительные целые ответы.
N совокупности цифр могут быть как четными, так и не четными. Рассмотрим понятие нечетности.
Нечетные (любые нечетные оканчиваются на цифры 1, 3, 5, 7, 9.) при делении на два имеют остаток. Например, 7:2=3,5, 11:2=5,5, 23:2=11,5.
Что значит четные N
Любые четные суммы классов оканчиваются на цифры: 0, 2, 4, 6, 8. При делении четных N на 2, остатка не будет, то есть в результате получается целый ответ. Например, 50:2=25, 100:2=50, 3456:2=1728.
Важно! Числовой ряд из N не может состоять только из четных или нечетных значений, так как они должны чередоваться: за четным всегда идет нечетное, за ним снова четное и т.д.
Свойства N
Как и все другие множества, N обладают своими собственными, особыми свойствами. Рассмотрим свойства N ряда (не расширенного).
Внимание! Все вышеперечисленные неравенства действительны и в обратном направлении.
Как называются компоненты умножения

Для того, чтобы быстро и правильно умножать и уметь решать обратные задачи, необходимо знать компоненты умножения.
15.10=150. В данном выражении 15 и 10 являются множителями, а 150 – произведением.
Умножение обладает свойствами, которые необходимы при решении задач, уравнений и неравенств:
Например: 15.Х=150. Разделим произведение на известный множитель. 150:15=10. Сделаем проверку. 15.10=150. По такому принципу решаются даже сложные линейные уравнения (если упростить их).
Важно! Произведение может состоять не только из двух множителей. Например: 840=2.5.7.3.4
Что такое натуральные числа в математике?
Разряды и классы натуральных чисел
Вывод
Подведем итоги. N используются при счете или обозначении количества предметов. Ряд натуральных совокупностей цифр бесконечен, но он включает в себя только целые и положительные суммы разрядов и классов. Умножение тоже необходимо для того, чтобы считать предметы, а также для решения задач, уравнений и различных неравенств.
Это интересно! Легкие правила округления чисел после запятой
Что такое натуральные числа
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое НАТУРАЛЬНЫЕ ЧИСЛА.
С ними человек встречается с самого рождения. Например, когда считает пальцы на руке – 1, 2, 3, 4, 5. Или отмечает праздники – 8 марта, 23 февраля, 9 мая, 31 декабря.
Натуральные числа — это.
Натуральные числа – это те числа, которые возникают при подсчете чего-либо. Например, одно яблоко, два яблока, пять яблок десять яблок и так далее.
Лучше даже представить, что вы подсчитываете людей, ибо их нельзя поделить на части, как большинство предметов (например, разрезов яблоко пополам).
Само слово «naturalis» в переводе с латинского означает «естественный».
Если число не является ни дробным, ни отрицательным, то его можно назвать натуральным.
Натуральными числами люди пользуются уже много тысячелетий. Просто у разных народов были разные системы исчисления. Например, римляне для счета использовали палочки. Так и появились знаменитые римские цифры – I, V, X, L, C, D и M.
А вот в Древнем Вавилоне использовали шестеричную систему. И до наших дней она дошла в виде часов, в которых 1 час равен 60 минутам, а 1 минута равна 60 секундам.
И наконец, современное обозначение цифр (0, 1, 2, 3, 4, 5 и так далее) принадлежит арабам, хотя за основу они взяли индийскую десятеричную систему и добавили к ней «ноль».
Натуральный ряд
Если расположить натуральные числа в порядке возрастания, то полученная цепочка будет называться натуральным рядом.
Он всегда появляется, когда нам нужно что-то посчитать поштучно. Например, в магазине мы обычно так делаем с овощами или фруктами, берем 5 морковок или 3 яблока. А уже только потом взвешиваем их, так как цены указаны за килограмм.
И конечно, именно так учатся считать школьники в первом классе. Например, если в задачке нарисовано пять флажков и вопрос звучит «сколько?», то любой ребенок будет считать «пальцем», отмечая каждый флажок и озвучивая натуральный ряд «один, два, три, четыре, пять».
Ну и тут же будет важным упомянуть, что количество натуральных чисел бесконечно. А значит, и натуральный ряд является бесконечным.
Это записано в основном законе натуральных чисел:
Каким бы большим не было натуральное число N, всегда найдется натуральное число N+1, которое будет больше.
Ноль — это натуральное число или нет
Натуральный ряд можно построить двумя способами:
Вы спросите, в чем разница? Во втором случае возможен вариант, когда нужного предмета может и не быть вовсе. И тогда его количество равно нулю.
То есть натуральный ряд начинается не с единицы, а с ноля. И выглядит вот так: 0, 1, 2, 3, 4, 5 и так далее.
Соответственно, в первом случае ноль нельзя считать натуральным числом. А во втором – можно. Интересно, что споры, какой подход более правильный, у математиков идут до сих пор. И сторонников обеих теорий примерно поровну.
Но у российских школьников проблем с выбором нет. В нашей стране придерживаются той версии, что ноль – это натуральное число.
Операции с натуральными числами
Школьники в младших классах на уроках математики имеют дело только с натуральными числами. Помимо самих цифр учатся и самым простым действиям:
Вот и все, что мы хотели рассказать о натуральных числах.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
А стоит ли себе забивать голову, какое число натуральное, а какое нет? Мир от этого не станет, ни проще, ни сложнее. Да и что неестественного в отрицательных числах? Если человеку не хватает денег, чтобы рассчитаться с долгами, то его имущество как раз уйдет в минус, отдал за долги всё, что было, но остался должен, значит необходимо ещё заработать, чтоб из минуса выйти в ноль.