Что такое натуральные числа 5 класс видеоурок
Натуральные числа
Урок 1. Подготовка к ОГЭ по математике 9 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Натуральные числа»
· повторить, какие числа входят в множество натуральных чисел;
· повторить классы и разряды натуральных чисел;
· повторить правила округления и сравнения натуральных чисел;
· повторить порядок выполнения действий над натуральными числами;
· повторить понятия делителя и кратного, основные признаки делимости;
· повторить алгоритмы вычисления наименьшего общего кратного и наибольшего общего делителя.
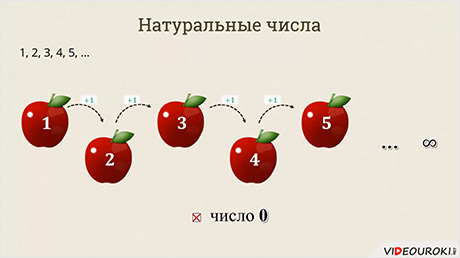
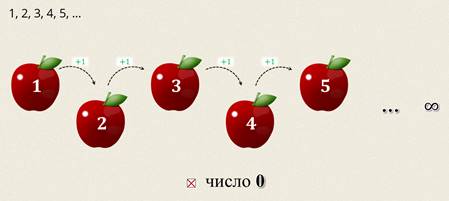
Ещё в самом раннем возрасте вы впервые познакомились с числами. Это были числа, которые можно использовать для счёта. Множество таких чисел называют множеством натуральных чисел.
Обратите внимание на то, что число 0 не входит в это множество.
Начиная со второго, каждое число натурального ряда на единицу больше предыдущего. Не трудно заметить, что этот ряд бесконечен. Причём есть наименьшее число, оно равно единице, а вот наибольшего числа нет.
Понятно, что с ростом чисел будут получаться двузначные, трёхзначные и так далее.
Сейчас напомним классы и разряды натуральных чисел.
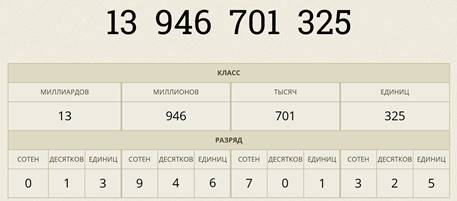
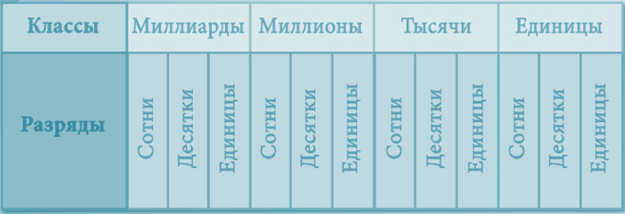
Рассмотрим такое число. Объединим цифры этого числа в тройки, начиная с конца. Так мы выделили классы числа. Крайний справа — класс единиц, далее — класс тысяч, класс миллионов и класс миллиардов.
К слову названия классов можно и продолжить: триллионы, квадриллионы, квинтиллионы, секстиллионы и септиллионы. Но на практике с такими большими числами мы не сталкиваемся, поэтому запоминать их названия не имеет никакого смысла.
Интересно то, что самое большое число назвать нельзя, но представить возможно. Сосчитав примерное количество частиц известной нам Вселенной, ученые показали, что оно представляет собой единицу с нулями в количестве от семидесяти девяти до восьмидесяти двух. Оно однозначно меньше единицы с сотней нулей. А вот это число имеет неофициальное название гугол. Оно то и позволит вам представить невообразимо большое число.
Вернёмся к нашему одиннадцатизначному числу. Чтобы прочитать его, поочерёдно будем называть числа, записанные в классах.
В данном случае это 13 миллиардов 946 миллионов 701 тысяча и 325 единиц.
Каждый класс имеет 3 разряда: разряд единиц, разряд десятков и разряд сотен.
Стоит напомнить, что числа 1, 10, 100 и так далее называются разрядными единицами.
С их помощью любое натуральное число можно записать в виде суммы разрядных слагаемых.
А сейчас поговорим об округлении натуральных чисел. Округлять натуральные числа можно до десятков, сотен, тысяч и так далее.
Повторим правило округления на конкретных примерах.
Далее давайте вспомним правила сравнение натуральных чисел.
Для этого могут быть использованы знаки больше, меньше либо равно.
Выражения, полученные в первых четырёх случаях, называют числовыми неравенствами.
А выражения, содержащие знак равно, называют числовыми равенствами.
Далее вспомним, какие действия можно выполнять над натуральными числами.
Вспомним определения делителя и кратного.
Среди всех натуральных чисел выделяют простые и составные.
Простыми называют натуральные числа, которые делятся на единицу и на само себя.
Приведём примеры простых чисел: 2, 3, 5, 7, 11, 13, 17, 19 и т.д.
Стоит отметить, что среди простых чисел есть только одно чётное — это число 2. И существует таблица простых чисел.
Все остальные числа называют составными. Они имеют более двух делителей.
Обратите внимание, что число 1 не относится ни к одной из групп. Ведь оно имеет только один делитель.
И вам уже известны некоторые признаки делимости, которые относительно быстро позволяют определять, является ли данное число кратным тому или иному.
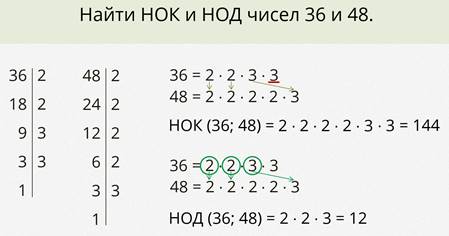
Понятно, что многие числа имеют общие кратные и общие делители, и часто при решении задач нужно находить наименьшее общее кратное (НОК) и наибольший общий делитель (НОД) двух и более чисел. Вспомним алгоритмы, которые помогут это сделать.
Но для начала напомним, как можно разложить число на простые множители.
Вот так мы с вами повторили все о натуральных числах.
А именно: какие числа входят в множество N натуральных чисел; классы и разряды натуральных чисел; правила их округления и сравнения; а также порядок выполнения действий над натуральными числами. Мы вспомнили понятия делителя и кратного, повторили основные признаки делимости и алгоритмы вычисления наименьшего общего кратного и наибольшего общего делителя.
Что такое натуральные числа 5 класс видеоурок
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке Вы познакомитесь с натуральными числами, научитесь их записывать, читать и классифицировать.
Натуральные числа — это числа, которые мы используем при счете предметов. Например, 1 — это первое натуральное число, 10, 23, 120 и т.д.
Натуральные числа, записанные последовательно, т.е. по порядку одно за другим, называют натуральным рядом или множеством натуральных чисел.
В натуральном ряду каждое следующее число на единицу больше предыдущего. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 и так далее.
Натуральный ряд бесконечен, наибольшего числа в нем нет. Самое маленькое натуральное число – это 1, а вот 0 не является натуральным числом, так как им мы не пользуемся при счете.
В общем виде множество натуральных чисел обозначают заглавной латинской буквой N. Записывают таким образом:
И читают как: множество натуральных чисел — это 1; 2; 3; 4 и так далее.
Все натуральные числа можно записать с помощью десяти цифр: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.
Такую запись чисел называют десятичной.
Если натуральное число состоит из одного знака – одной цифры, то его называют однозначным, например, числа 3, 5, 9 – однозначные.
Так же по числу знаков в данном числе дают названия и другим числам. Например: 145, 809 – это трехзначные числа.
Существуют четырехзначные, пятизначные числа и так далее.
Двузначные, трехзначные и так далее числа называют многозначными.
Для чтения многозначное натуральное число разбивают справа налево на группы по три цифры в каждом (самая левая группа может состоять из одной или двух цифр). Эти группы называют классами. Каждая из трех цифр класса обозначает разряд: разряд единиц, разряд десятков, разряд сотен.
Классификация начинается справа. Три первые цифры справа составляют класс единиц, три следующие – класс тысяч, далее идет класс миллионов, затем – миллиардов. (см. Рис.). Так как ряд натуральных чисел бесконечен, то за миллиардами идут триллионы, за триллионами — триллиарды и т.д.
Миллион – это тысяча тысяч, его записывают с помощью единицы и шести нулей.
Миллиард – это тысяча миллионов. Его записывают с помощью единицы и 9 нулей.
Как же правильно прочитать многозначное число? Начинают читать многозначное число слева направо, по очереди называют число единиц каждого класса и добавляют название класса. При этом название класса единиц не называют, как и класса, в котором все три цифры — нули.
Например, вот это число (42 135 308) разбивают на классы так: оно имеет 308 единиц, 135 единиц в классе тысяч, 42 единицы в классе миллионов. Поэтому читают его так: 42 миллиона 135 тысяч 308.
Любое натуральное число можно представить в виде суммы разрядных единиц.
32 537 = 30 000 + 2 000 + 500 + 30 + 7
Таким образом, в этом уроке Вы познакомились с понятием натурального числа и натурального ряда, научились читать и классифицировать натуральные многозначные числа, а также раскладывать их по разрядам.
Натуральные числа и нуль
Видеоурок по этой теме можно посмотреть по ссылке: Натуральные числа и ноль.
Пройти тест по теме «Натуральные числа и действия над ними» можно по ссылке. Проверьте свои знания!
Нас повсюду окружают предметы. Так было раньше, и так будет всегда. И очень часто необходимо знать, сколько у нас или где-то еще есть тех или иных предметов: яблок, машин, людей, денег и т.д.
Еще в очень глубокой древности, когда не было не только науки математики, но и даже такого понятия как число, древние люди проводили подсчет при помощи наиболее близких для них инструментов – собственных частей тела: «Там столько буйволов, сколько на моих руках пальцев», или: «Мы поймали рыбы столько, сколько пальцев на руках у меня и тебя».
Со временем они заметили, что десять буйволов, десять рыб, десять врагов и т.д. объединяет то, что рассказывая об этом, люди употребляют одинаковое описание: «сколько на моих руках пальцев». То есть, они обнаружили, что группы разных предметов обладают одним схожим свойством – количеством, и что удобнее назвать одинаковое количество чего-либо обобщенным названием, которое будет определять эту величину. И вместо: «Мы поймали столько рыбы, сколько пальцев на моих руках» люди начали говорить: «Мы поймали десять рыб». Так появились числа, которые впоследствии были названы натуральными. Подробнее об истории возникновения чисел можно почитать по ссылке.
Натуральные числа – это те числа, при помощи которых мы осуществляем счет предметов: 1, 2, 3, 4, 5 и т.д
Число 1 (один) имеет еще одно название: единица.
Если к единице приложить еще единицу, к получившемуся результату еще одну, потом еще, и еще и т.д., то мы получим ряд натуральных чисел или просто натуральный ряд: один, два, три, четыре, пять и т.д.
Любое натуральное число можно представить в виде единицы или собрания нескольких единиц.
Начинается натуральный ряд чисел с единицы, то есть, с числа 1 (один).
Каждое последующее число ряда отличается от предыдущего на единицу.
Любое натуральное число больше нуля.
Нуль не относится к натуральному ряду чисел. В некоторых англоязычных странах его включают в этот ряд, но в отечественной математике принято по-другому. Действительно, нуль означает отсутствие чего-либо, «ни одной единицы», «ни одного», «ничего». А поскольку ряд натуральных чисел состоит из единицы и совокупности сложений единиц, то число «ни одной единицы» не может находиться в этом ряду.
Нуль обладает такими свойствами:
Математика. 5 класс
Простые и составные числа
Поиск простых чисел
Необходимо запомнить
По тому, на какие числа можно разделить натуральные числа, их можно классифицировать на простые и составные.
Натуральные числа – это 1, а также множество простых и составных чисел.
1 – это не простое и не составное число.
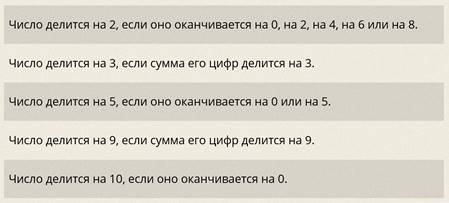
Если число оканчивается цифрой 0, то оно делится на 10.
Если сумма цифр делится на 3, то и само число делится на 3.
Если сумма цифр делится на 9, то и само число делится на 9.
Если число оканчивается одной из цифр: 0, 2, 4, 6, 8, – то оно делится на 2.
Если число оканчивается одной из цифр: 0 или 5, – то оно делится на 5.
Решето Эратосфена
Простые числа учёные пытались найти ещё в Древней Греции. Так, во II веке до н.э. Эратосфен придумал способ получения ряда простых чисел. Этот алгоритм назвали «решето Эратосфена». Суть заключается в том, что путём отсеивания составных чисел определяются простые. Опишем этот алгоритм для нахождения простых чисел от 1 до 100.
Для начала запишем все числа от 1 до 100.
1 вычеркнем, т.к. это число не простое и не составное. Выделим 2 – это первое простое число – и далее вычеркнем все кратные ему числа до ста (4,6,8 и т. д., то есть каждое второе число). Далее отметим следующее простое число – это 3. Вычеркнем все кратные ему числа до ста (6,9,12 и т.д., то есть каждое третье число).
Повторяем все шаги пока возможно с остальными простыми числами. В результате получается искомая таблица простых чисел.
Видеоурок по математике «Умножение натуральных чисел» для 5 класса
В этом уроке Вы увидите как можно умножать два натуральных числа. Все примеры представлены визуально, урок построен очень интересно.
Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями!
 | Минпросвещения планирует обновить федеральный перечень учебников |
 | «Молодые профессионалы»: среднее профессиональное образование должно стать востребованным |
 | Сергей Кравцов рассказал о проекте по обновлению правил русского языка |
 | В Министерстве просвещения разработали меморандум по воспитательной работе в школах |
 | Поздравляем с наступающим Днём учителя! |
Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала.
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьими лицами.
Администрация сайта готова оказать поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены