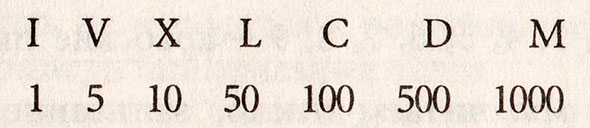Что такое натуральные числа в математике 2 класс примеры правило
Что такое натуральные числа
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое НАТУРАЛЬНЫЕ ЧИСЛА.
С ними человек встречается с самого рождения. Например, когда считает пальцы на руке – 1, 2, 3, 4, 5. Или отмечает праздники – 8 марта, 23 февраля, 9 мая, 31 декабря.
Натуральные числа — это.
Натуральные числа – это те числа, которые возникают при подсчете чего-либо. Например, одно яблоко, два яблока, пять яблок десять яблок и так далее.
Лучше даже представить, что вы подсчитываете людей, ибо их нельзя поделить на части, как большинство предметов (например, разрезов яблоко пополам).
Само слово «naturalis» в переводе с латинского означает «естественный».
Если число не является ни дробным, ни отрицательным, то его можно назвать натуральным.
Натуральными числами люди пользуются уже много тысячелетий. Просто у разных народов были разные системы исчисления. Например, римляне для счета использовали палочки. Так и появились знаменитые римские цифры – I, V, X, L, C, D и M.
А вот в Древнем Вавилоне использовали шестеричную систему. И до наших дней она дошла в виде часов, в которых 1 час равен 60 минутам, а 1 минута равна 60 секундам.
И наконец, современное обозначение цифр (0, 1, 2, 3, 4, 5 и так далее) принадлежит арабам, хотя за основу они взяли индийскую десятеричную систему и добавили к ней «ноль».
Натуральный ряд
Если расположить натуральные числа в порядке возрастания, то полученная цепочка будет называться натуральным рядом.
Он всегда появляется, когда нам нужно что-то посчитать поштучно. Например, в магазине мы обычно так делаем с овощами или фруктами, берем 5 морковок или 3 яблока. А уже только потом взвешиваем их, так как цены указаны за килограмм.
И конечно, именно так учатся считать школьники в первом классе. Например, если в задачке нарисовано пять флажков и вопрос звучит «сколько?», то любой ребенок будет считать «пальцем», отмечая каждый флажок и озвучивая натуральный ряд «один, два, три, четыре, пять».
Ну и тут же будет важным упомянуть, что количество натуральных чисел бесконечно. А значит, и натуральный ряд является бесконечным.
Это записано в основном законе натуральных чисел:
Каким бы большим не было натуральное число N, всегда найдется натуральное число N+1, которое будет больше.
Ноль — это натуральное число или нет
Натуральный ряд можно построить двумя способами:
Вы спросите, в чем разница? Во втором случае возможен вариант, когда нужного предмета может и не быть вовсе. И тогда его количество равно нулю.
То есть натуральный ряд начинается не с единицы, а с ноля. И выглядит вот так: 0, 1, 2, 3, 4, 5 и так далее.
Соответственно, в первом случае ноль нельзя считать натуральным числом. А во втором – можно. Интересно, что споры, какой подход более правильный, у математиков идут до сих пор. И сторонников обеих теорий примерно поровну.
Но у российских школьников проблем с выбором нет. В нашей стране придерживаются той версии, что ноль – это натуральное число.
Операции с натуральными числами
Школьники в младших классах на уроках математики имеют дело только с натуральными числами. Помимо самих цифр учатся и самым простым действиям:
Вот и все, что мы хотели рассказать о натуральных числах.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
А стоит ли себе забивать голову, какое число натуральное, а какое нет? Мир от этого не станет, ни проще, ни сложнее. Да и что неестественного в отрицательных числах? Если человеку не хватает денег, чтобы рассчитаться с долгами, то его имущество как раз уйдет в минус, отдал за долги всё, что было, но остался должен, значит необходимо ещё заработать, чтоб из минуса выйти в ноль.
Числа. Натуральные числа.
Простейшее число — это натуральное число. Их используют в повседневной жизни для подсчета предметов, т.е. для вычисления их количества и порядка.
Что такое натуральное число: натуральными числами называют числа, которые используются для подсчета предметов либо для указывания порядкового номера любого предмета из всех однородных предметов.
В натуральном ряду каждое число больше предыдущего на единицу.
Сколько чисел в натуральном ряду? Натуральный ряд бесконечен, самого большого натурального числа не существует.
Десятичной так как 10 единиц всякого разряда образуют 1 единицу старшего разряда. Позиционной так как значение цифры зависит от её места в числе, т.е. от разряда, где она записана.
Для подсчета времени в градусной мере углов существует шестидесятеричная система счисления (основа число 60). В 1 часе — 60 минут, в 1 минуте — 60 секунд; в 1 угловом градусе — 60 минут, в 1 угловой минуте — 60 секунд.
Всякое натуральное число легко записать в виде разрядных слагаемых.
Числа 1, 10, 100, 1000. – это разрядные единицы. При их помощи натуральные числа записывают как разрядные слагаемые. Таким образом, число 307 898 в виде разрядных слагаемых записывается так:
307 898 = 300 000 + 7 000 + 800 + 90 + 8
Обозначение натуральных чисел: Множество натуральных чисел обозначают символом N.
Классы натуральных чисел.
Всякое натуральное число возможно написать при помощи 10-ти арабских цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Сравнение натуральных чисел.
Таблица разрядов и классов чисел.
1-й разряд единицы тысяч
2-й разряд десятки тысяч
3-й разряд сотни тысяч
1-й разряд единицы миллионов
2-й разряд десятки миллионов
3-й разряд сотни миллионов
4-й класс миллиарды
1-й разряд единицы миллиардов
2-й разряд десятки миллиардов
3-й разряд сотни миллиардов
Числа от 5-го класса и выше относятся к большим числам. Единицы 5-го класса — триллионы, 6-го класса — квадриллионы, 7-го класса — квинтиллионы, 8-го класса — секстиллионы, 9-го класса — ептиллионы.
Основные свойства натуральных чисел.
Действия над натуральными числами.
1. Сложение натуральных чисел результат: сумма натуральных чисел.
Формулы для сложения:
В основном, сложение натуральных чисел выполняется « столбиком ».
2. Вычитание натуральных чисел – операция, обратная сложению: разница натуральных чисел.
Формулы для вычитания:
Вычитание натуральных чисел удобно производить « столбиком ».
3. Умножение натуральных чисел : произведение натуральных чисел.
Формулы для умножения:
(а + b) ∙ с= а ∙ с + b ∙ с
(а – b) ∙ с = а ∙ с – b ∙ с
4. Деление натуральных чисел – операция, обратная операции умножения.
Формулы для деления:
Числовые выражения и числовые равенства.
Запись, где числа соединяются знаками действий, является числовым выражением.
Записи, где знаком равенства объединены 2 числовых выражения, является числовыми равенствами. У равенства есть левая и правая части.
Порядок выполнения арифметических действий.
Когда числовое выражение состоит из действий только одной степени, то их выполняют последовательно слева направо.
Когда в выражении есть скобки – сначала выполняют действия в скобках.
Например, 36:(10-4)+3∙5= 36:6+15 = 6+15 = 21.
Натуральные числа в математике — определение, свойства, примеры
В данной статье мы рассмотрим натуральные числа и все, что с ними связано. Сначала узнаем, какие из них можно называть таковыми, каковы их признаки. Далее поговорим о различных классах данного вида, общих и специфических свойствах. Обязательно затронем сравнение натуральных чисел и неравенства с их участием, а также алгоритм выполнения арифметических преобразований.
Понятие
Данное понятие появилось в математике одним из первых. В древности люди перечисляли предметы на пальцах, и им вполне этого хватало. Но с бурным развитием торговли и ростом количества продукции на рынках одних пальцев для счета стало не хватать. Поэтому древние люди придумали символы, обозначающие количество чего-либо, которые они использовали для перечисления скота, различных вещей и т.д. Чуть позже числа вошли в науку математику, где стали активно применяться в качестве материала для многочисленных алгебраических преобразований.
Натуральные числа — все символы, используемые при счете каких-либо предметов, тем самым вычисляя их последовательность и количество. Все отрицательные и дробные числа не являются натуральными.
Важно! Нуль не входит в натуральное множество, то есть не является одним из них, потому мы и не применяем его при счете.
Соответственно — наименьшей является единица. Наибольшего натурального числа не существует, так как счет можно продолжать до бесконечности.

Вернемся в древние времена. Тогда числа записывали чаще с помощью палочек или любых других примитивных знаков:
Но когда палочек приходилось писать слишком много (100, 1000), люди задумались над более емкой системой записи количества предметов. Так, арабы придумали и завезли в Европу свои цифры, которые на континенте назвали арабскими. Мы прекрасно знаем все эти цифры:
0 1 2 3 4 5 6 7 8 9 (10 штук).
Из данных цифр можно составить абсолютно все натуральные числа.
Их множество обозначается знаком N.
Натуральный ряд
Разберем еще одно понятие, связанное с главной темой.
Натуральный ряд — последовательная запись всех натуральных символов. Как мы уже выяснили, высшего натурального числа не существует, поэтому данный ряд представляет собой последовательность, которая не заканчивается.
Каждый последующий символ натурального ряда больше предыдущего ровно на единицу.
Разряды и классы
Для начала скажем, что при счете мы обычно применяем десятичную систему исчисления. Она подразумевает то, что 10 единиц низшего разряда образуют 1 единицу более старшего, и данная закономерность сохраняется до конца счета.
Разрядные единицы — это такие символы, которые обозначают начало определенного разряда.
Пример : 1, 10, 100 и т.д.
Благодаря разрядным единицам, можно сделать запись менее длинной и более упрощенной.
Пример: Записать 298 481 в виде суммы разрядных слагаемых.
Решение: 200 000 + 90 000 + 8 000 + 400 + 80 + 1.
Важно! 12-ти разрядные числа называются большими и редко употребляются в алгебраических вычислениях.
Если число состоит из одного знака, то оно называется однозначным. Соответственно — различают двузначные, трехзначные, четырехзначные и т.д.
Теперь стоит немного рассказать и о натуральных классах.
При чтении определенного числа его разделяют на классы, включающие по три разряда. Первые три единицы представляют собой класс единиц, следующие три — класс тысяч. Далее идут довольно крупные группы — классы миллионов, миллиардов и другие. Помните, что каждая цифра любого класса является разрядом, то есть классы состоят из разрядов.
Сравнивать их можно через классы или разряды. Соответственно — то число, где количество старших разрядов преобладает, является более крупным по значению.
Главные свойства
Рассмотрим основные свойства, которые характерны для всех натуральных чисел. Они применимы всегда и везде, так как способствуют упрощению некоторых выражений различных типов. Их используют при различных вычислениях и преобразованиях.
Свойство 1
От перемены места слагаемых сумма не меняется.
Пример: 2 + 1 = 1 + 2 = 3. Как бы мы не переставляли слагаемые, сумма все равно останется такой же.
Свойство 2
От перемены места множителей произведение не меняется.
Пример: 2 х 1 = 1 х 2 = 2. Аналогичное правило есть и в умножении. Значение произведения в итоге остается тем же.
Свойство 3
Чтобы прибавить к числу сумму двух других чисел, можно сначала произвести сложение одного числа, а затем — второго.
Пример : 2 + (3 + 10) = 3 + (2 + 10) = 15. Данное правило еще называется сочетательным свойством.
Свойство 4
Чтобы умножить на число произведение двух других чисел, можно сначала произвести умножение одного числа, а затем — второго.
Пример: 5 х (6 х 4) = (5 х 6) х 4 = 120. Правило, аналогичное предыдущему, только здесь используется другой вид арифметических действий. Принцип остается тем же.
Свойство 5
Для того, чтобы умножить сумму натуральных чисел на другое число, нужно умножить это число на каждую из представленных слагаемых, а затем сложить полученные произведения чисел.
Пример: 5 х (4 + 3) = 5 х 4 + 5 х 3 = 35. Это правило умножения числа относительно сложения двух других. Часто применяется в решении заданий по преобразованию каких-либо выражений.
Мы выяснили и разобрали на примерах самые главные свойства натуральных чисел. Если вы их не знали раньше, то советуем вам обратить на них особое внимание. А теперь перейдем к изучению наиболее распространенных и часто используемых операций.
Характерные операции и взаимодействия
Конечно, с данным видом чисел можно выполнять очень много различных действий. Однако мы разберем те основные операции, которые не выводят конечный результат из натурального множества.
Сложение
Один из наиболее простейших видов взаимодействий. Здесь мы берем две части (два слагаемых) и соединяем (складываем) их, образуя конечный результат — сумму.
Пример: 6 + 2 = 8. Восемь в данном случае будет являться суммой двух слагаемых — шести и двух.
Вычитание
Вид операций, противоположный предыдущему. В данном случае имеем уже три составляющих. То выражение, из которого мы вычитаем определенное количество, называется уменьшаемым. Количество. которое уже отделено от первоначального, называется вычитаемым. А конечный результат, соответственно, именуется разностью, то есть подразумевается разность между двумя количествами.
Пример : 8 — 2 = 6. Восемь — уменьшаемое, два — вычитаемое, шесть — разность.
Умножение
Вид операций, при которой одно число берется такое количество раз, которое равно второму. Оба исходных числа называются множителями. Результат взаимодействия именуется произведением.
Пример: 6 х 5 = 30. Шесть и пять — множители, тридцать — произведение чисел.
Деление
Вид операций, противоположный умножению. Число, подвергаемое делению, носит название делимого, а то, на которое делят именуется делителем. Результат деления называется частным.
Существует деление с остатком. После такого деления остается небольшой остаток, который уже не делится на исходный делитель. Так как мы разбираем натуральный вид, то и ответ должен получиться натуральным, поэтому в данном случае мы лишь приписываем остаток к ответу.
Пример: 6 : 2 = 3. Шесть — делимое, 2 — делитель, 3 — частное.
Пример деления с остатком: 7 : 3 = 2 (1) — ответ записываем в виде натурального числа. Один — остаток. Остальное по аналогии с предыдущим примером.
Возведение в степень
Такой вид арифметических операций, при котором число умножается на себя количество раз, равное указанной степени. Здесь мы имеем три элемента: исходное число, степень и ответ.
Пример : 6 3 = 6 х 6 х 6 = 216.
Порядок решения — пример
Итак, после подробного разбора основных арифметических операций рассмотрим алгоритм выполнения всех указанных действий в одном равенстве. Возьмем какой-нибудь пример, включающий в себя большинство всех представленных выше взаимодействий.
(36 + 76) х (85 — 80) + 96 ÷ 3 =
Сначала необходимо выполнить те действия, которые расположены в скобках, то есть требуется раскрыть скобки слева направо. Раскроем скобки в нашем примере и получим следующее выражение:
Далее также слева направо выполняем все действия умножения и деления, соответственно — мы получим следующую сумму:
Наконец, производим финальное действие — сложение:
592 — конечный результат.
Таким образом, мы узнали, что натуральные числа — это все целые и положительные числа, нуль не является таковым. Вникли в небольшую предысторию данных символов и поняли их важное значение в математике. Произвели разбор основных свойств и арифметических действий, производимых с ними. Также рассмотрели алгоритм действий, необходимых для вычисления ответа.
Чтобы проверить свои знания по изученной теме, рекомендуем вам пройти тест, представленный ниже, а также посмотреть видео, где вы найдете еще больше примеров решения различных уравнений с натуральными числами.
Натуральные числа
Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и т. д.
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
Какие операции возможны над натуральными числами
Записывайтесь на курсы обучения математике для учеников с 1 по 11 классы!
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это примеры неправильной записи натуральных чисел, потому что ноль расположен слева. Число не может начинаться с нуля. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двузначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа самого на себя | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 × 8) |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами: