Что такое нечеткие высказывания
Что такое нечеткие высказывания
Нечеткие высказывания со степенью истины 0,5 называются индифферентностью, поскольку оно истинно в той же мере, что и ложно. Пример.
Определение. Отрицанием нечеткого высказывания А является высказывание 
степень истинности которого определяется выражением 
. Из этого определения следует, что степень ложности 
совпадает со степенью истинности для 
.
Определение. Конъюнкцией нечетких высказываний А и В, называется нечеткое высказывание 
степень истинности которого совпадает со степенью истинности менее истинного высказывания.
Определение. Дизъюнкцией нечетких высказываний А и 
называется нечеткое высказывание 
степень истинности которого совпадает со степенью истинности более истинного высказывания 
Определение. Импликацией нечетких высказываний А и 
называется нечеткое высказывание 
степень истинности которого 
Истинность импликации не меньше чем степень ложности ее посылки или степень истинности ее следствия. Пример.
Пусть нечеткое высказывание А имеет степень истинности 0,3; нечеткое высказывание 
. Импликация этих высказываний 
будет иметь степень истинности 
.
Степень импликации тем выше, чем меньше степень истинности посылки или больше степень истинности следствия.
Определение. Эквивалентностью нечетких высказываний 
и 
называется нечеткое высказывание
Истинность эквивалентности совпадает со степенью истинности менее истинной из импликаций 
и 
Если степень истинности высказываний 0 или 1, то все определения соответствуют логическим операциям над четкими высказываниями.
Определение. Два высказывания 
и 
называются нечетко близкими, если степень истинности 
больше или равна 0,5. В последнем случае будем называть 
и 
взаимно нечетко индифферентными.
Порядок выполнения операций над нечеткими высказываниями
Вычислим степень истинности составного нечеткого высказывания
Нечеткие лингвистические высказывания
Нечетким лингвистическим высказыванием будем называть высказывания следующих видов:
1. Высказывание «b есть а», где
b – наименование лингвистической переменной,
а – ее значение, которому соответствует отдельный лингвистический терм из базового терм-множества Т лингвистической переменной b.
2. Высказывание «b есть Va», где V — модификатор, соответствующий таким словам, как: «ОЧЕНЬ», «БОЛЕЕ ИЛИ МЕНЕЕ», «МНОГО БОЛЬШЕ» и другим, которые могут быть получены с использованием процедур операций концентрации и растяжения данной лингвистической переменной.
3. Составные высказывания, образованные из высказываний видов 1 и 2 и нечетких логических операций в форме связок: «И», «ИЛИ», «ЕСЛИ-ТО», «НЕ».
Пример. Рассмотрим некоторые примеры нечетких высказываний. Первое из них — «скорость автомобиля высокая» представляет собой нечеткое высказывание первого вида, в рамках которого лингвистической переменной «скорость автомобиля» присваивается значение «высокая».
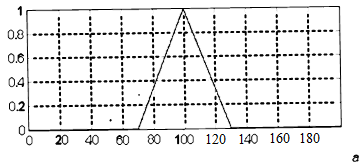
При этом предполагается, что на универсальном множестве Х переменной «скорость автомобиля» определен соответствующий лингвистический терм «высокая», который задается в форме функции принадлежности некоторого нечеткого множества (например, рис. а).
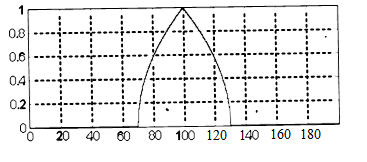
Нечеткое высказывание второго вида «скорость автомобиля очень высокая» означает, что лингвистической переменной «скорость автомобиля» присваивается значение «высокая» с модификатором «ОЧЕНЬ», который изменяет значение соответствующего лингвистического терма «высокая» на основе использования некоторой расчетной формулы, например формулы для операции концентрации CON(A) нечеткого множества A для терма «высокая».
Нечеткое высказывание второго вида «скорость автомобиля более или менее высокая» означает, что лингвистической переменной «скорость автомобиля» присваивается значение «высокая» с модификатором «БОЛЕЕ ИЛИ МЕНЕЕ», который изменяет значение соответствующего лингвистического терма «высокая» на основе использования некоторой расчетной формулы, например формулы для операции растяжения DIL(A) нечеткого множества A для терма «высокая».
Наконец, нечеткое высказывание третьего вида «скорость автомобиля высокая и расстояние до перекрестка близкое» означает, что одной лингвистической переменной «скорость автомобиля» присваивается значение «высокая», а другой лингвистической переменной «расстояние до перекрестка» присваивается значение «близкое». Эти нечеткие высказывания первого вида соединены логической операцией нечеткая конъюнкция (операцией нечеткое «И»).
Правила нечетких продукций
Продукционная нечеткая система представляет собой некоторое согласованное множество отдельных правил нечетких продукций в форме: «ЕСЛИ А ТО В», где А и В— нечеткие лингвистические высказывания вида 1, 2 или 3.
Простейший вариант правила нечеткой продукции, который наиболее часто используется в системах нечеткого вывода, может быть записан в форме:
1. ПРАВИЛО 1: ЕСЛИ «b1 есть а1», ТО «b2 есть а2». (7.1)
Здесь нечеткое высказывание «b1 есть а1» представляет собой условие данного правила нечеткой продукции, а нечеткое высказывание «b2 есть а2» – нечеткое заключение данного правила.
Часто ситуация может соответствовать более сложному случаю, когда высказывания, относящиеся к разным лингвистическим переменным соединены нечеткими логическими операциями в условии правила нечеткой продукции.
Этот вариант правил нечетких продукций может быть записан в следующей общей форме:
2. ПРАВИЛО 2: ЕСЛИ «b1 есть а1» И (ИЛИ) «b2 есть а2» ТО «b3 есть v» (7.2)
Здесь нечеткие высказывания: («b1 есть а1» И «b2 есть а2«), («b1 есть а1» ИЛИ «b2 есть а2«) представляют собой условия правил нечетких продукций, а нечеткое высказывание » b3 есть v » — заключение правил.
Каждое из нечетких высказываний «b1 есть а1«, «b2 есть а2» называют подусловиями данных правил нечетких продукций.
Наконец, нечеткими логическими операциями могут быть соединены нечеткие высказывания, относящиеся к разным лингвистическим переменным в заключении правила нечеткой продукции.
Этот вариант правил нечетких продукций может быть записан в следующей общей форме:
3. ПРАВИЛО 3: ЕСЛИ «b1 есть a1‘» ТО «b2 есть а2» И (ИЛИ) «b3 есть v» (7.3)
Здесь нечеткое высказывание «b1 есть а» представляет собой условие правил нечетких продукций, а нечеткие высказывания: («b2 есть a2» И «b3 есть v»), («b2 есть a2» ИЛИ «b3 есть v») — заключения данных правил.
Каждое из нечетких высказываний «b2 есть a2«, «b3 есть v» называют подзаключениями данного правила нечеткой продукции.
Что такое нечеткие высказывания
Логическое отрицание нечеткого высказывания A обозначается ¬ A – это унарная (т.е. производимая над одним аргументом) логическая операция, результат которой является нечетким высказыванием «не A », «неверно, что A », значение истинности которого:
Помимо приведенного выше исторически принятого основного определения нечеткого логического отрицания (нечеткого «НЕ»), введенного Заде, могут использоваться следующие альтернативные формулы:
Логическая конъюнкция нечетких высказываний A и B обозначается A ∩ B – это бинарная (т.е. производимая над двумя аргументами) логическая операция, результат которой является нечетким высказыванием « A и B », значение истинности которого:
Помимо приведенного выше исторически принятого основного определения логической конъюнкции (нечеткого «И»), введенного Заде, могут использоваться следующие альтернативные формулы:
T A ∩ B = T A T B – в базисе Бандлера-Кохоута;
T A ∩ B = max T A + T B − 1 ; 0 – в базисе Лукашевича-Гилеса;
Логическая дизъюнкция нечетких высказываний A и B обозначается A ∪ B – это бинарная логическая операция, результат которой является нечетким высказыванием « A или B », значение истинности которого:
Помимо приведенного выше исторически принятого основного определения логической дизъюнкции (нечеткого «ИЛИ»), введенного Заде, могут использоваться следующие альтернативные формулы:
T A ∪ B = T A + T B − T A T B – в базисе Бандлера-Кохоута;
T A ∪ B = min T A + T B ; 1 – в базисе Лукашевича-Гилеса;
Помимо приведенного выше исторически принятого основного определения нечеткой импликации, введенного Заде, могут использоваться следующие альтернативные определения нечеткой импликации, предложенные различными исследователями в области теории нечетких множеств:
T A ⊃ B = max 1 − T A ; T B – Гедель;
T A ⊃ B = min T A ; T B – Мамдани;
T A ⊃ B = min 1 ; 1 − T A + T B – Лукашевич;
T A ⊃ B = min T A + T B ; 1 – Лукашевич-Гилес;
T A ⊃ B = T A T B – Бандлер-Кохоут;
T A ⊃ B = max T A T B ; 1 − T A – Вади;
Общее число введенных определений нечеткой импликации не ограничивается приведенными выше. Большое количество работ по изучению различных вариантов нечеткой импликации обусловлено тем, что понятие нечеткой импликации является ключевым при нечетких выводах и принятии решений в нечетких условиях. Наибольшее применение при решении прикладных задач нечеткого управления находит нечеткая импликация Заде.
Нечеткая эквивалентность нечетких высказываний A и B обозначается A ≡ B – это бинарная логическая операция, результат которой является нечетким высказыванием « A эквивалентно B », значение истинности которого:
Так же, как в классической бинарной логике, в нечеткой логике с помощью рассмотренных выше логических связок можно формировать достаточно сложные логические высказывания.
Прямой нечеткий логический вывод
Введение
В 1965 г. в журнале «Information and Control» была опубликована работа Л.Заде под названием «Fuzzy sets». Это название переведено на русский язык как нечеткие множества. Побудительным мотивом стала необходимость описания таких явлений и понятий, которые имеют многозначным и неточный характер. Известные до этого математические методы, использовавшие классическую теорию множеств и двузначную логику, не позволяли решать проблемы этого типа.
При помощи нечетких множеств можно формально определить неточные и многозначные понятия, такие как «высокая температура» или «большой город». Для формулирования определения нечеткого множества необходимо задать так называемую област рассуждений. Например, когда мы оцениваем скорость автомобиля, мы ограничимся диапазоном X = [0, Vmax], где Vmax — максимальная скорость, которую может развить автомобиль. Необходимо помнить, что X — четкое множество.
Основные понятия
Нечетким множеством A в некотором непустом пространстве X называется множество пар 
где
— функция принадлежности нечеткого множества A. Эта функция приписывает каждому элементу x степень его принадлежности нечеткому множеству A.
Продолжив предыдущий пример, рассмотрим три неточные формулировки:
— «Малая скорость автомобиля»;
— «Средняя скорость автомобиля»;
— «Большая скорость автомобиля».
На рисунке представлены нечеткие множества, соответствующие приведенным формулировкам, с помощью функций принадлежности.
В фиксированной точке X=40км/ч. функция принадлежности нечеткого множества «малая скорость автомобиля» принимает значением 0,5. Такое же значение принимает функция принадлежностинечеткого множества «средняя скорость автомобиля», тогда как для множества «большая скорость автомобиля» значение функции в этой точке равно 0.
Однако, в отличие от традиционной логики, главным инструментом нечеткой логики будет не правило modus ponens, а так называемое композиционное правило вывода, весьма частным случаем которого является правило modus ponens.
Предположим, что имеется кривая y=f(x) и задано значение x=a. Тогда из того, что y=f(x) и x=a, мы можем заключить, что y=b=f(a).
Обобщим теперь этот процесс, предположив, что a — интервал, а f(x) — функция, значения которой суть интервалы. В этом случае, чтобы найти интервал y=b, соответствующий интервалу a, мы сначала построим множество a’ с основанием a и найдем его пересечение I с кривой, значения которой суть интервалы. Затем спроектируем это пересечение на ось OY и получим желаемое значение y в виде интервала b. Таким образом, из того, что y=f(x) и x=A — нечеткое подмножество оси OX, мы получаем значение y в виде нечеткого подмножества B оси OY.
Пусть U и V — два универсальных множества с базовыми переменными u и v, соответственно. Пусть A и F — нечеткие подмножества множеств U и U x V. Тогда композиционное правило вывода утверждает, что из нечетких множеств A и F следует нечеткое множество B = A * F.
Реализация
Входные данные будут содержать знания (нечеткие множества) и правила (импликации), например:
A = <(x1, 0.0), (x2, 0.2), (x3, 0.7), (x4, 1.0)>.
B = <(x1, 0.7), (x2, 0.4), (x3, 1.0), (x4, 0.1)>.
A => B.
Импликация будет представлена в виде декартовой матрицы, каждый элемент которой рассчитывается с помощью выбранного оператора импликации (в данном примере — функции Гёделя):
Для данных выше это будет:
Conclusion:
A => B.
x1 x2 x3 x4
x1 1.0 1.0 1.0 1.0
x2 1.0 1.0 1.0 0.1
x3 1.0 0.4 1.0 0.1
x4 0.7 0.4 1.0 0.1
Далее в результате вывода получается новое множество:
Презентация была опубликована 8 лет назад пользователемМаргарита Карпова
Похожие презентации
2 Высказывания на множестве значений фиксированной ЛП Значения ЛП соответствуют нечетким множествам одного и того же универса Х Модификатор (связка) Операции над НМ оченьCON недополнение И ИЛИ Пример: ЛП «толщина изделия» Х = [10, 80] T= <"малая", "средняя", "большая">A 1 A 2 A 3 ВысказываниеНМ
НМ на универсе X x Y c функцией принадлежности: исходное высказывание новая ЛП значение новой ЛП 2)Правило преобразования дизъюнктивной формы: =>» title=»Правила преобразования нечетких высказываний вида 3 1)Правило преобразования конъюнктивной формы: => НМ на универсе X x Y c функцией принадлежности: исходное высказывание новая ЛП значение новой ЛП 2)Правило преобразования дизъюнктивной формы: =>» > 4 Правила преобразования нечетких высказываний вида 3 1)Правило преобразования конъюнктивной формы: => НМ на универсе X x Y c функцией принадлежности: исходное высказывание новая ЛП значение новой ЛП 2)Правило преобразования дизъюнктивной формы: => НМ на универсе X x Y c функцией принадлежности: исходное высказывание новая ЛП значение новой ЛП 2)Правило преобразования дизъюнктивной формы: =>»> НМ на универсе X x Y c функцией принадлежности: исходное высказывание новая ЛП значение новой ЛП 2)Правило преобразования дизъюнктивной формы: =>»> НМ на универсе X x Y c функцией принадлежности: исходное высказывание новая ЛП значение новой ЛП 2)Правило преобразования дизъюнктивной формы: =>» title=»Правила преобразования нечетких высказываний вида 3 1)Правило преобразования конъюнктивной формы: => НМ на универсе X x Y c функцией принадлежности: исходное высказывание новая ЛП значение новой ЛП 2)Правило преобразования дизъюнктивной формы: =>»>
b’)> новая ЛП значение новой ЛП Нечеткое отношение xRy c функцией принадлежности: НМ AНМ B Правило Мамдани» title=»3)Правило преобразования импликативной формы: => b’)> новая ЛП значение новой ЛП Нечеткое отношение xRy c функцией принадлежности: НМ AНМ B Правило Мамдани» > 5 3)Правило преобразования импликативной формы: => b’)> новая ЛП значение новой ЛП Нечеткое отношение xRy c функцией принадлежности: НМ AНМ B Правило Мамдани b’)> новая ЛП значение новой ЛП Нечеткое отношение xRy c функцией принадлежности: НМ AНМ B Правило Мамдани»> b’)> новая ЛП значение новой ЛП Нечеткое отношение xRy c функцией принадлежности: НМ AНМ B Правило Мамдани»> b’)> новая ЛП значение новой ЛП Нечеткое отношение xRy c функцией принадлежности: НМ AНМ B Правило Мамдани» title=»3)Правило преобразования импликативной формы: => b’)> новая ЛП значение новой ЛП Нечеткое отношение xRy c функцией принадлежности: НМ AНМ B Правило Мамдани»>