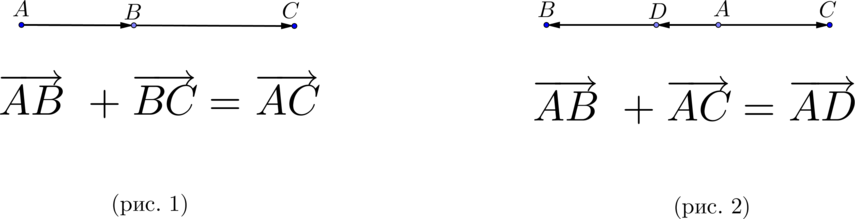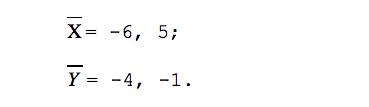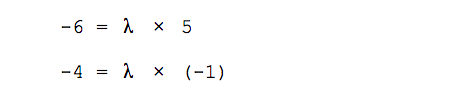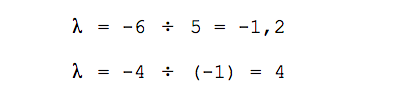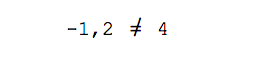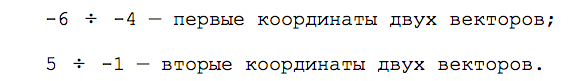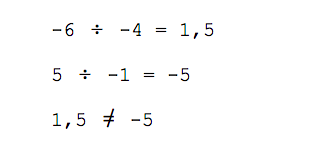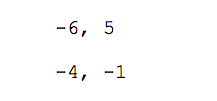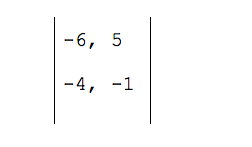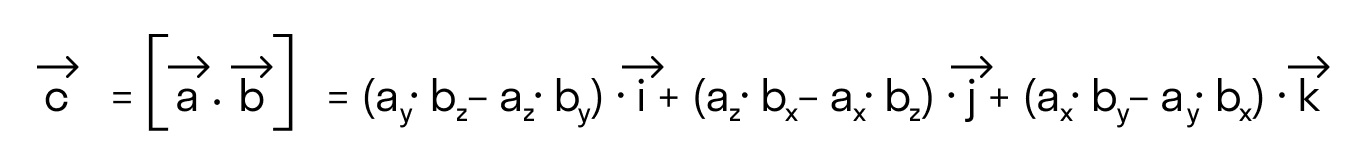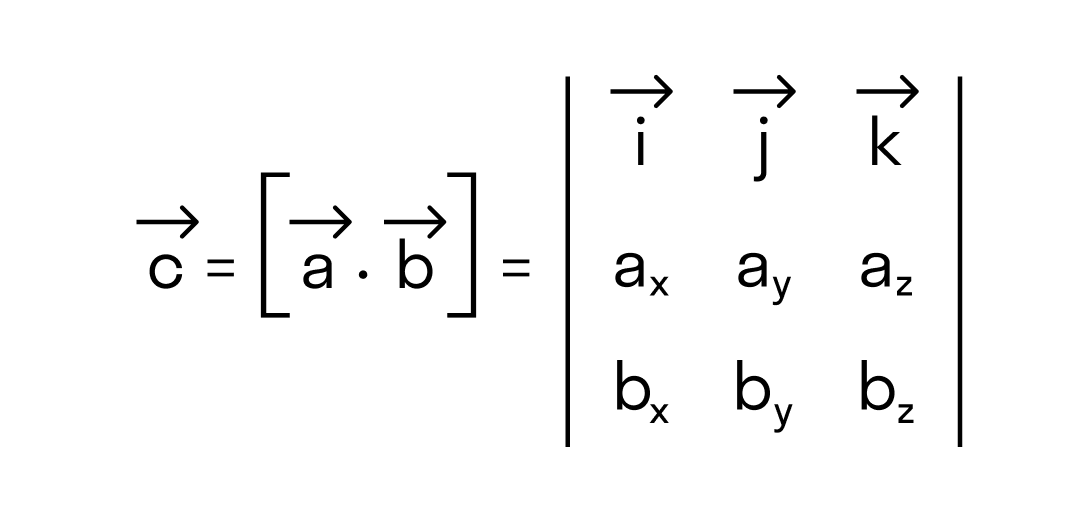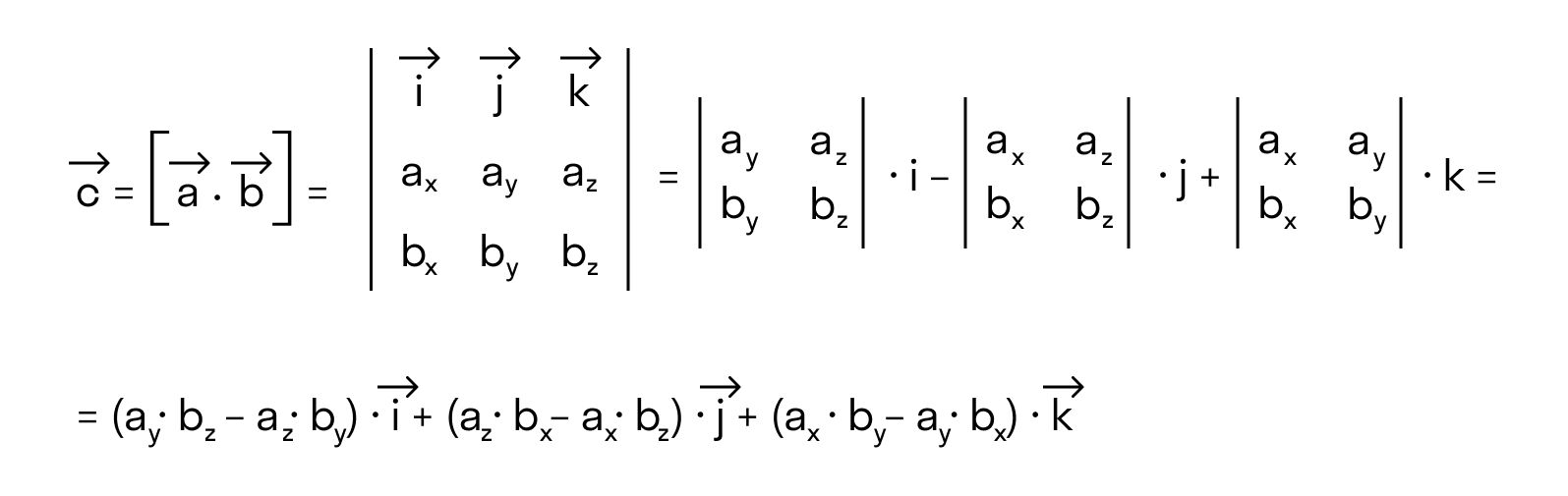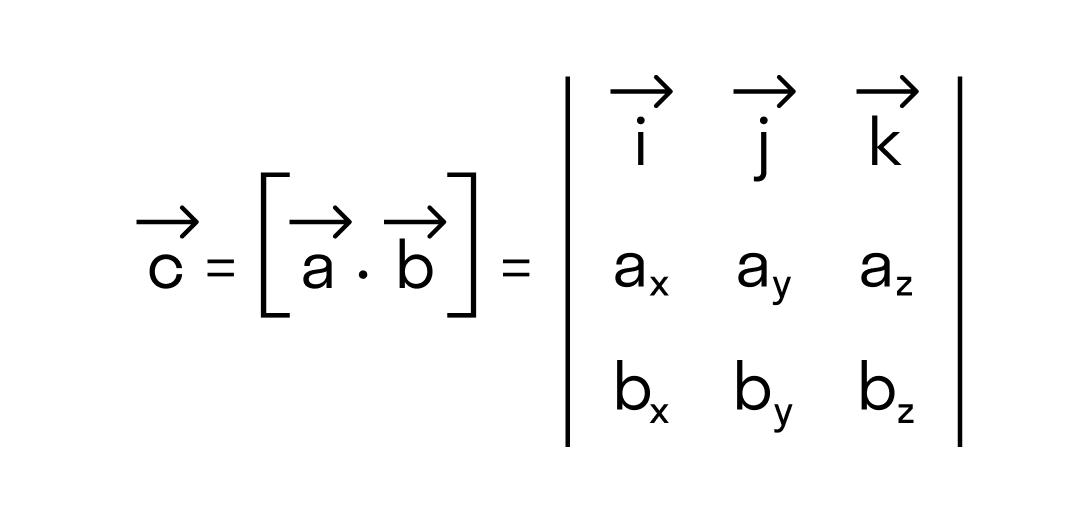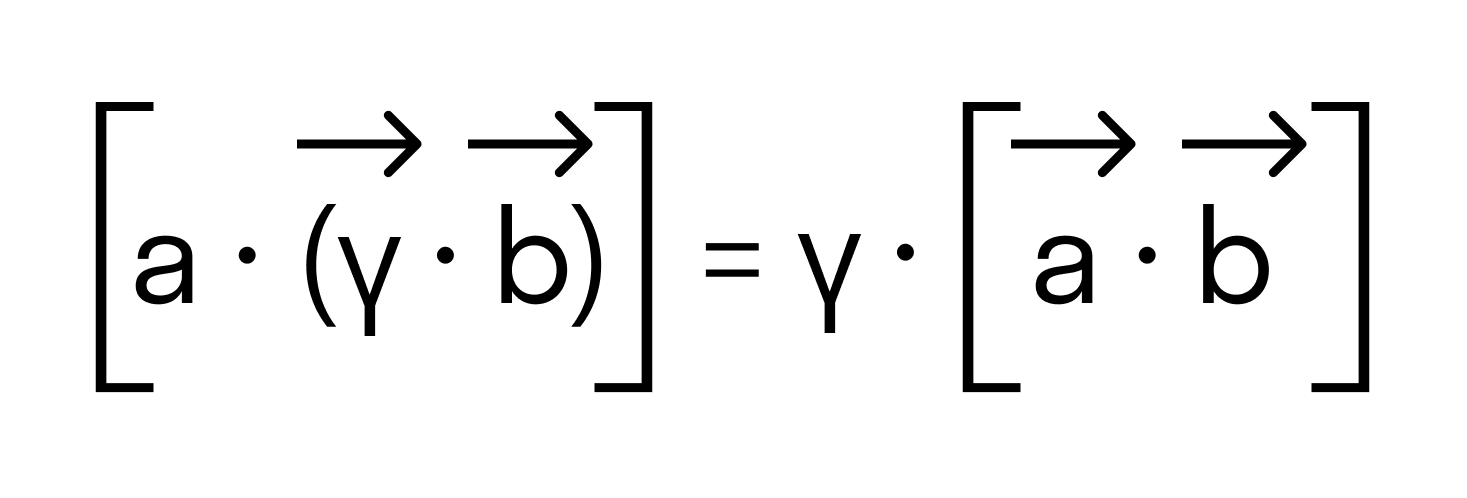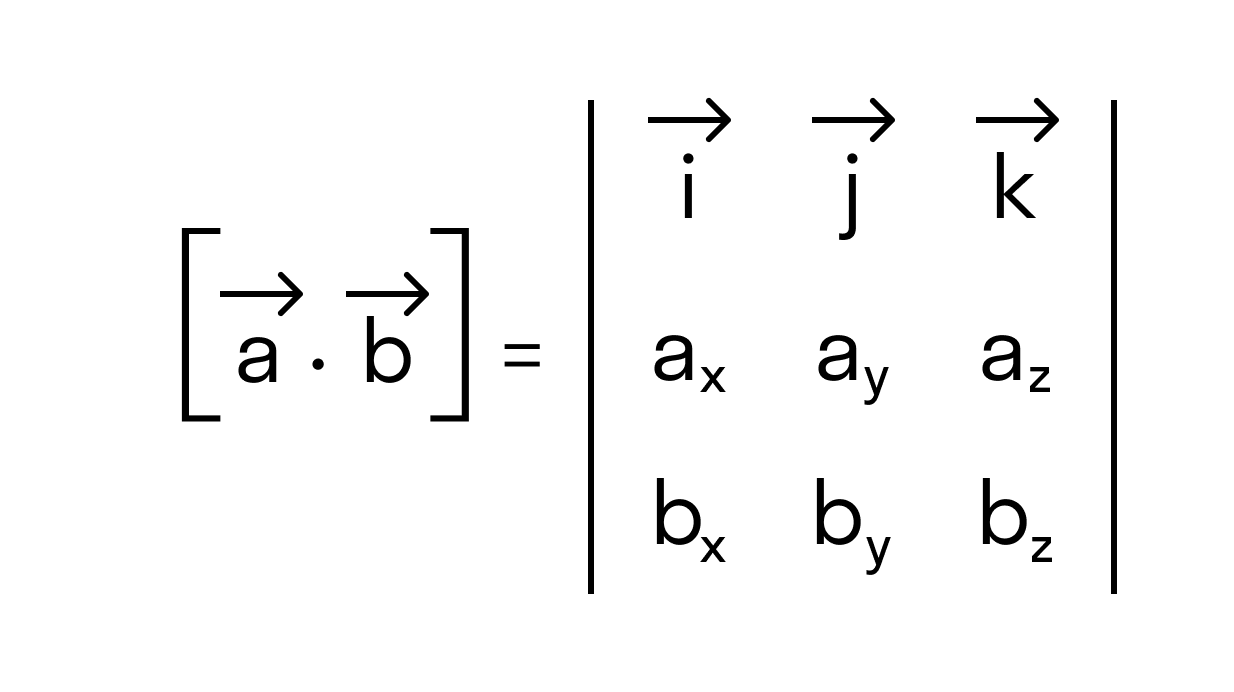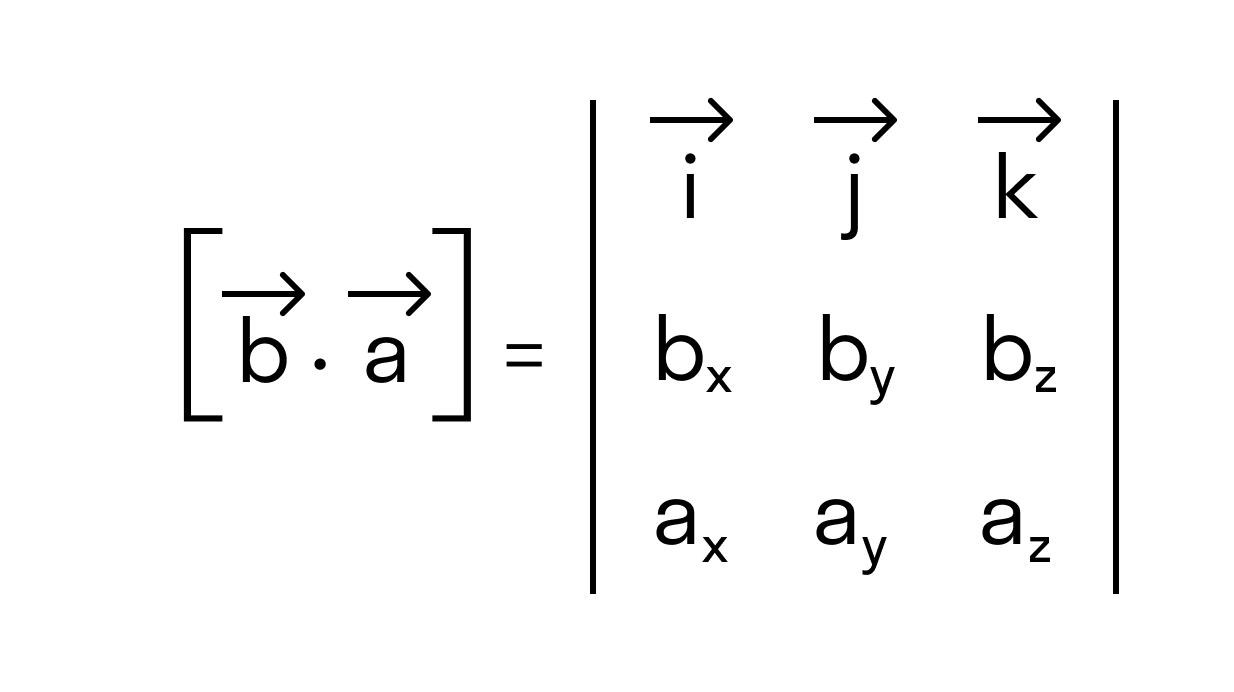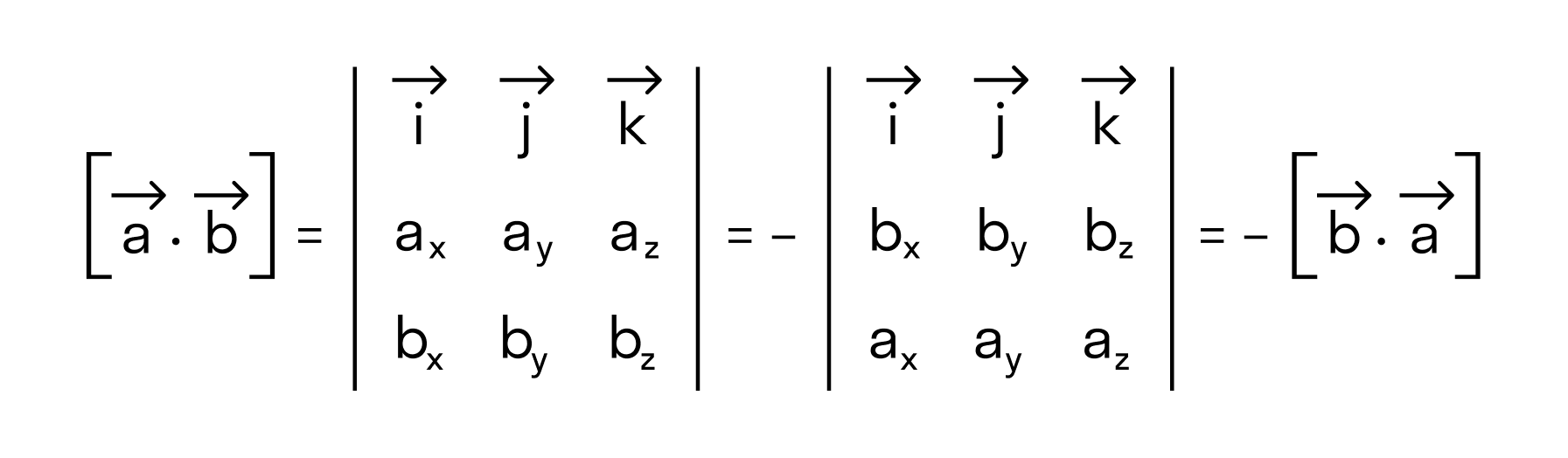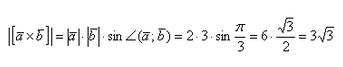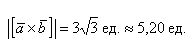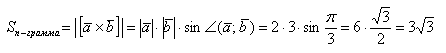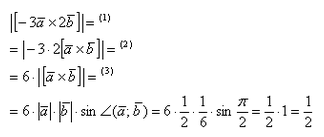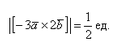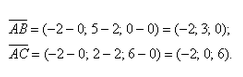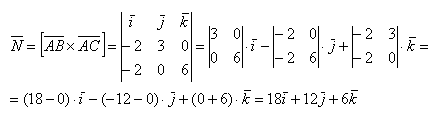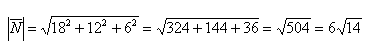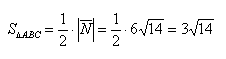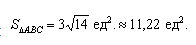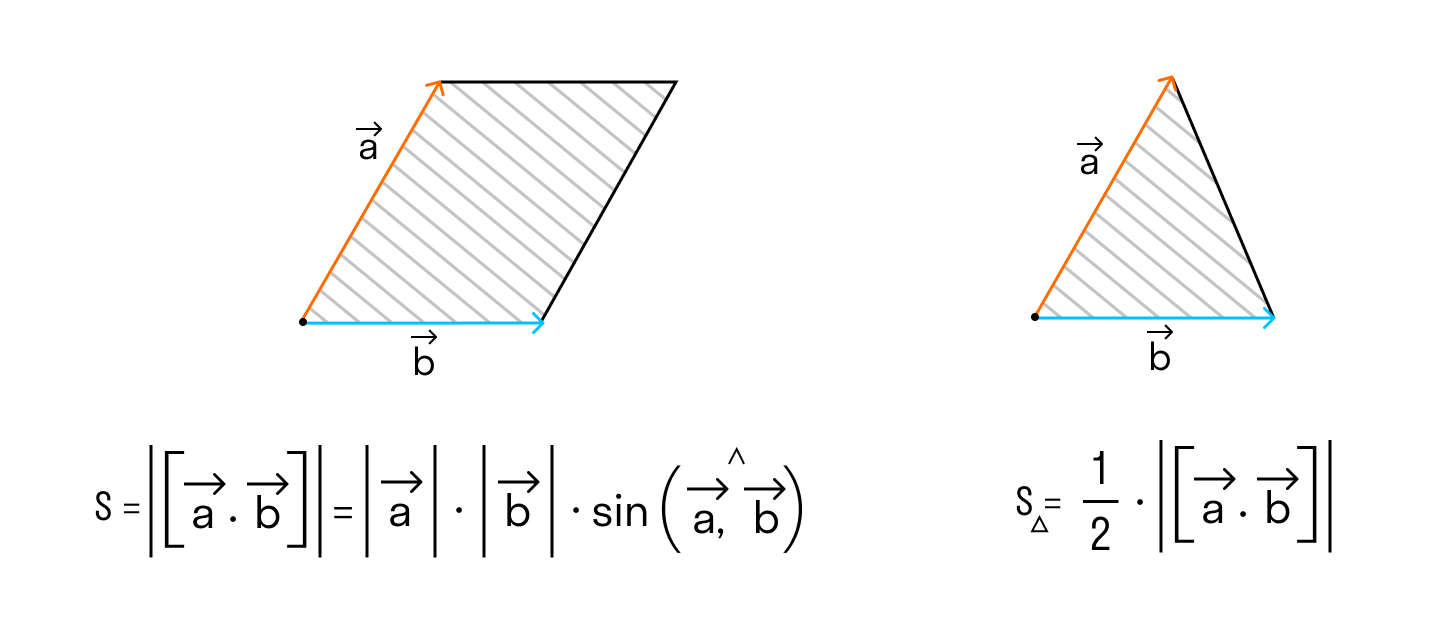Что такое неколлинеарный вектор в геометрии

Определение вектора

В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.

Для начала дадим определение:

Вектор – это направленный отрезок прямой.

Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.

Нулевой вектор

Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.

Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.

Длина вектора

Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.

Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.

Коллинеарность векторов

Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.

Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.

Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.

Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.

Направление векторов

Считается, что нулевой вектор является сонаправленым к любым другим векторам.

Равные и противоположные векторы

Равными называются сонаправленные вектора, у которых длины равны.

Противопожными называются противоположно направленные вектора, у которых их длины равны.

Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.

Углы между векторами

Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .

Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.

Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).

Источник

Векторы. Начальные сведения

Определения

Если длина вектора равна нулю (совпадают начало и конец), то такой вектор называют нулевым.

Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых ( \(\overrightarrow a, \overrightarrow b\) и \(\overrightarrow c\) ).

В противном случае векторы называются неколлинеарными (например, \(\overrightarrow a\) и \(\overrightarrow d\) ).

Векторы называются равными, если они сонаправлены и их длины равны.

Правила сложения коллинеарных векторов:

\(\blacktriangleright\) Для того, чтобы сложить два сонаправленных вектора, можно отложить второй вектор от конца первого. Тогда их сумма – вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго (рис. 1).

\(\blacktriangleright\) Для того, чтобы сложить два противоположно направленных вектора, можно отложить второй вектор от начала первого. Тогда их сумма – вектор, начало которого совпадает с началом обоих векторов, длина равна разности длин векторов, направление совпадает с направлением большего по длине вектора (рис. 2).

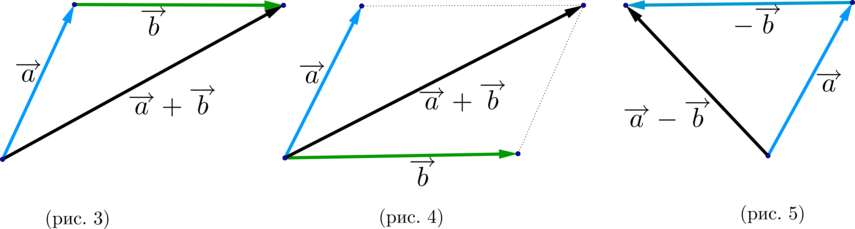
Правила сложения неколлинеарных векторов \(\overrightarrow \) и \(\overrightarrow\) :

\(\blacktriangleright\) Правило треугольника (рис. 3).

\(\blacktriangleright\) Правило параллелограмма (рис. 4).

Определение

Вектор \(\overrightarrow <-b>\) – это вектор, противоположно направленный с вектором \(\overrightarrow \) и совпадающий с ним по длине.

Свойства сложения векторов

Замечание

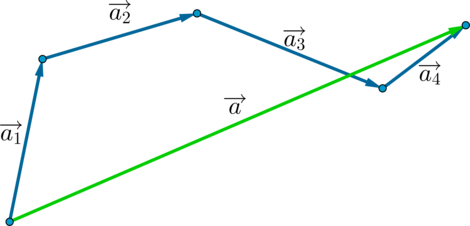
Для того, чтобы сложить несколько вектором, можно отложить их последовательно: каждый следующий от конца предыдущего. Тогда суммой этих векторов будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего: \[\overrightarrow +\overrightarrow +\overrightarrow + \overrightarrow =\overrightarrow \]

Определение

Свойства произведения вектора на число

1. Сочетательный закон: \(k(\lambda\overrightarrow )=(k\lambda)\overrightarrow \) ;

Теорема

Источник

Векторы: третий уровень сложности

Знакомимся с коллинеарностью.

Для большинства людей искусственный интеллект — это нечто сложное и таинственное. А для математиков это синоним фразы «перемножение матриц». С точки зрения человека, который владеет линейной алгеброй, в искусственном интеллекте нет ничего загадочного.

Мы хотим, чтобы вы тоже смогли понять искусственный интеллект на уровне математики. Для этого у нас идёт цикл статей про линейную алгебру:

Сама тема несложная, но конкретно этот шаг вам ничего не даст в практическом смысле. Но если вам хватит терпения, на базе этих знаний мы уже перейдём к матрицам.

Что за коллинеарность

Представьте два вектора, которые находятся в одной плоскости и располагаются параллельно друг другу. При этом у них может быть разная длина. Такое расположение делает связку векторов коллинеарными, или, по-простому, линейно зависимыми.

И наоборот: если вектора находятся в одной плоскости и располагаются не параллельно друг относительно друга, то их считают линейно независимыми — неколлинеарными. Пока что ничего сложного.

Коллинеарные векторы Неколлинеарные векторы

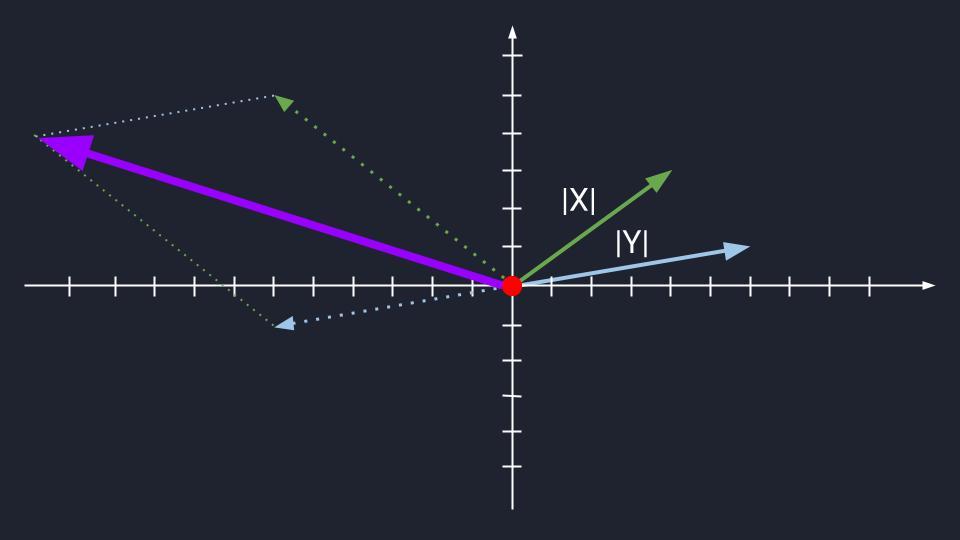
Сложение коллинеарных и неколлинеарных векторов

Очевидно, что сложить два коллинеарных вектора очень легко: откладываем второй вектор от начала первого, получится новый вектор. Он будет коллинеарным своим слагаемым, они все будут лежать, грубо говоря, на одной линии.

Можно представить, что вы идёте прямо: каждый ваш шаг — это вектор. Каждый новый шаг — новый вектор. Но если все их сложить, получится один большой прямой вектор длиной как все ваши шаги.

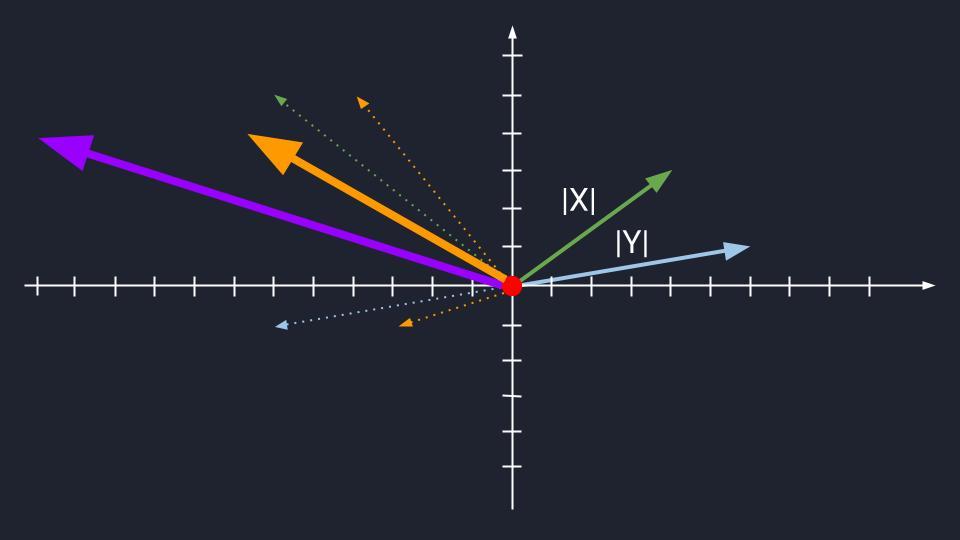
Теперь попробуем сложить пару неколлинеарных векторов. Это как если бы мы сначала сделали шаг немного правее, а потом сделали бы шаг влево. Шага два, но если соединить начало и конец пути, он не будет совпадать с траекториями наших шагов. Появится какой-то новый вектор, с новым направлением, и он будет неколлинеарным по отношению к своим слагаемым.

Также пару неколлинеарных векторов из одной плоскости можно растянуть и развернуть в пространстве. Если их сложить, также появится новый вектор.

У математиков такой вектор называют базисом. Когда базис находится на плоскости или в пространстве, то он может единственным образом превращаться обратно в пару неколлинеарных векторов, которые его сформировали.

Правило работает, когда мы масштабируем и меняем расположение векторов в пространстве. Если мы изменим направление исходных векторов, то получим новый базис.

Базис — понятие из высшей математики, поэтому, если сейчас сложно, не отчаивайтесь. Студенты-математики когда-то тоже отчаивались.

Мы изменили пару неколлинеарных векторов и сформировали из них базис — получили новый фиолетовый вектор с собственной системой координат Теперь мы изменили исходные неколлинеарные векторы и получили новый базис — это оранжевый вектор

Как определять неколлинеарность

Когда мы работаем с короткими векторами, всё очевидно: нарисовали систему координат, отложили на ней векторы, они либо совпали, либо не совпали. Если совпали — коллинеарные, если нет — неколлинеарные.

А теперь представьте, что вектора настолько огромные, что мы физически не можем их нарисовать и сопоставить. Например,

Как такое нарисовать? Как проверить коллинеарность? Вот тут начинается магия алгебры.

Есть три способа проверки линейной зависимости векторов. Для простоты вычислений проверим эти три способа на вот этих всё ещё простых векторах:

По этим координатам ответим на два вопроса: являются ли предложенные вектора линейно зависимыми (то есть коллинеарными) и можно ли их раскладывать по базису.

Первый способ. Запишем простую систему уравнений: возьмём первую координату каждого вектора и приравняем её ко второй координате каждого вектора, умноженной на неизвестное число λ. Вычислим λ и сравним результаты.

👉 Знак λ здесь по традиции и для удобства. На самом деле это просто некое неизвестное число. Вместо этой буквы могли быть X, Y, Z или N, но так как у нас вектора уже называются X и Y, а N в математике используется для других целей, возьмём λ — это греческая буква «лямбда», давний предок нашей русской буквы «Л».

Составляем систему уравнений:

Вычисляем значение λ:

Сравниваем результат и делаем вывод:

Мы получили разное значение для неизвестного числа λ и поэтому наши векторы будут считаться линейно независимыми. Из них можно получить базис.

Если бы значение λ совпало, то мы бы имели дело с линейно зависимыми векторами.

Второй способ. Проверяем координаты векторов на пропорциональность: берём первую координату первого вектора, делим её на первую координату второго вектора. Повторяем это же действие со вторыми координатами: берём вторую координату первого вектора и делим её на вторую координату второго вектора.

Получаем такую пропорцию:

Считаем значение и сравниваем результат:

Равенство не выполняется, и поэтому между векторами нет зависимости.

Третий способ. Используем четыре элемента наших координат для поиска определителя — скалярной величины, с которой мы подробно познакомимся в следующих статьях во время решения матричных уравнений. Сейчас нам не нужны подробности, и для проверки линейной зависимости достаточно формулы.

Записываем в две строки координаты наших векторов:

Переводим координаты векторов в определитель — добавляем с двух сторон вертикальную черту и получаем простую квадратную матрицу размером 2 на 2:

В полученной матрице две диагонали. Числа −6 и −1 образуют главную диагональ; числа −4 и 5 — вторую диагональ. Чтобы найти определитель, нам нужно умножить числа главной и второй диагонали, а затем вычесть их разницу.

Если из координат вектора мы получили определитель и он не равен нулю, то векторы считаются линейно независимыми и подходят для разложения по базису.

И наоборот: нулевой определитель указывает на линейную зависимость векторов.

Что из этого нужно запомнить

Что дальше

Следующий шаг — матрицы. Это те самые, которые лежат в основе всех нейронок и искусственного интеллекта. Матрица — это таблица чисел, с которыми можно проводить различные вычисления.

Источник

Векторное произведение векторов

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Определение векторного произведения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

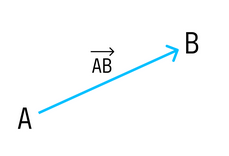
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.

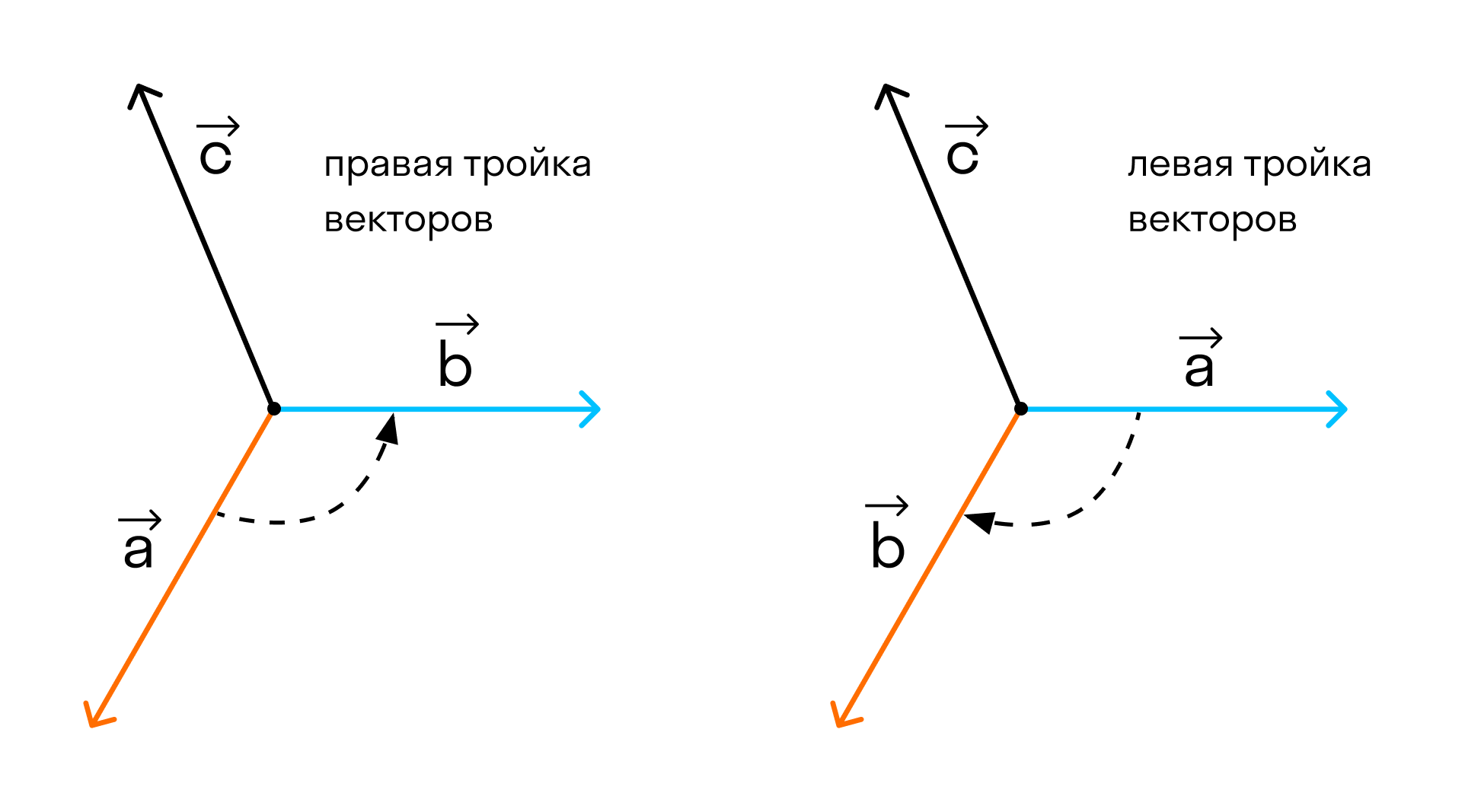
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.

Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.

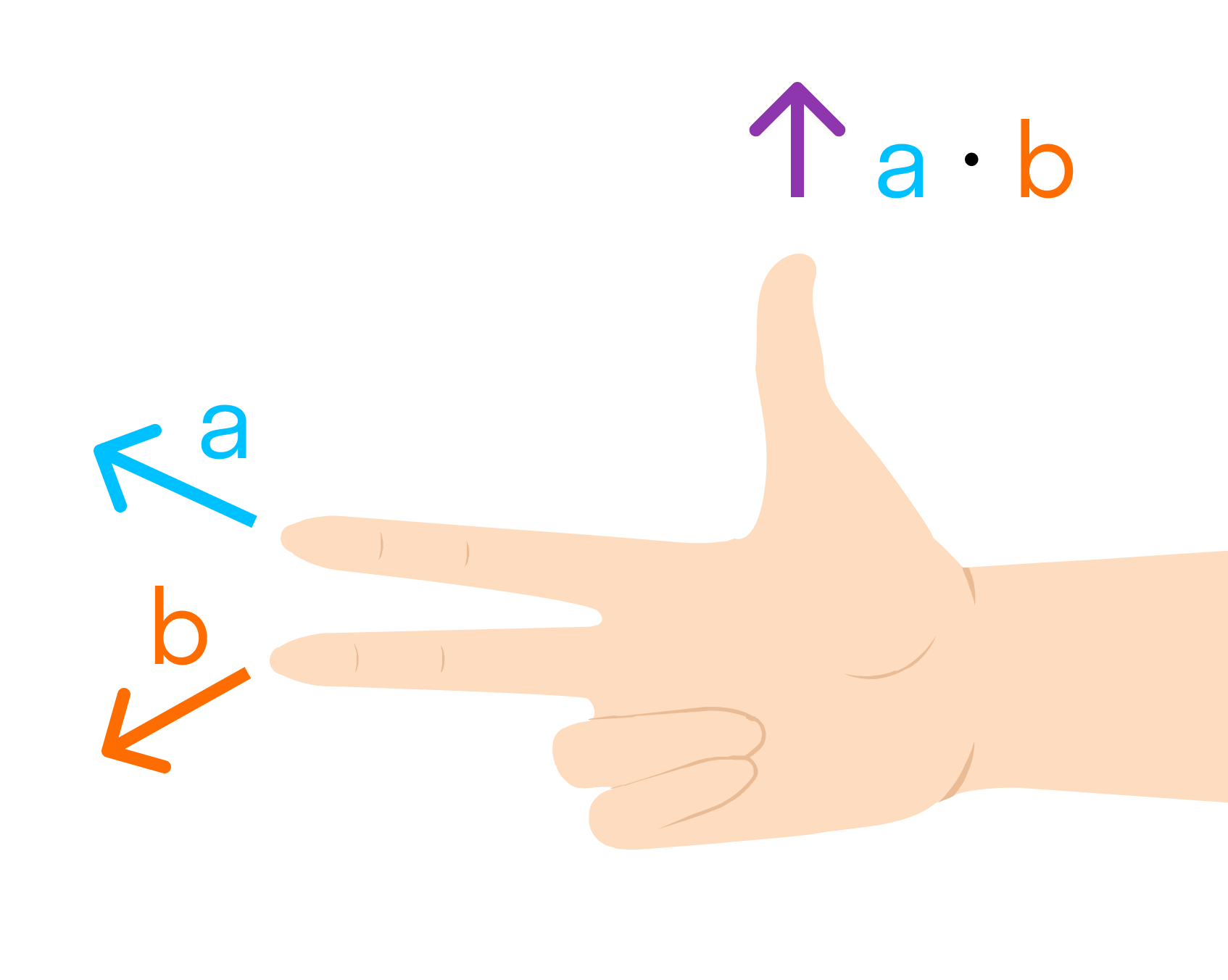
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.

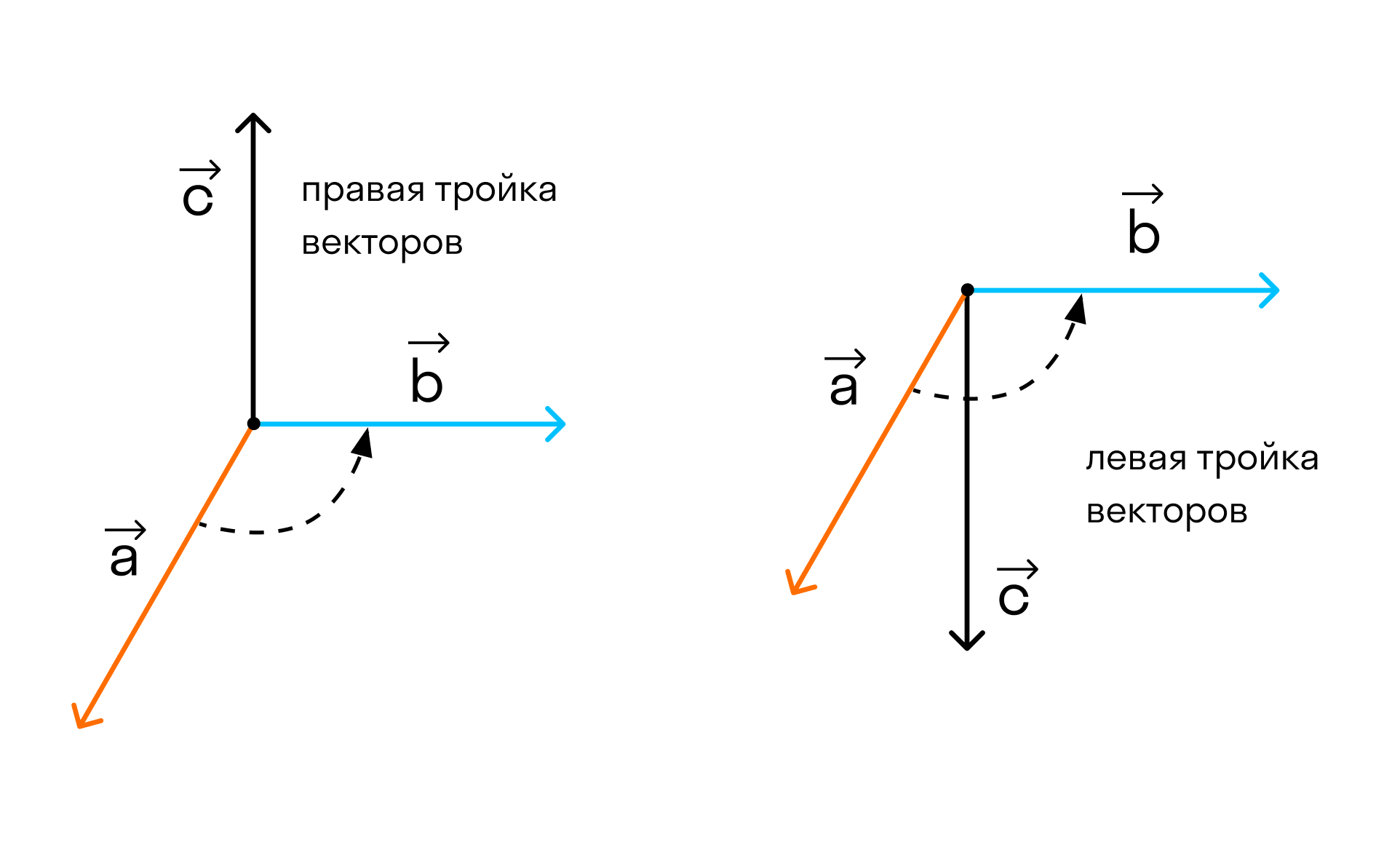
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.

Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.

В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.

И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.

Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!

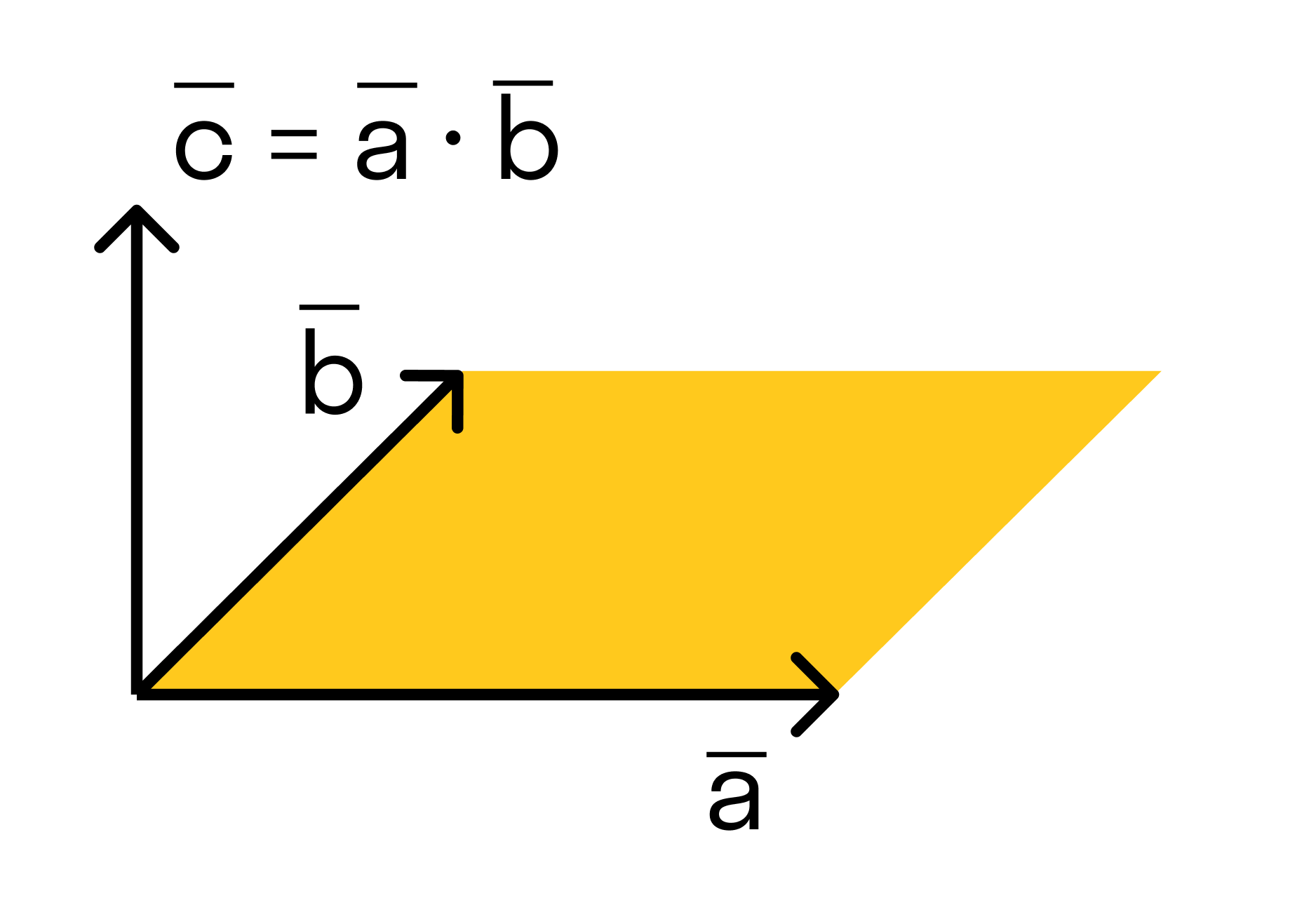
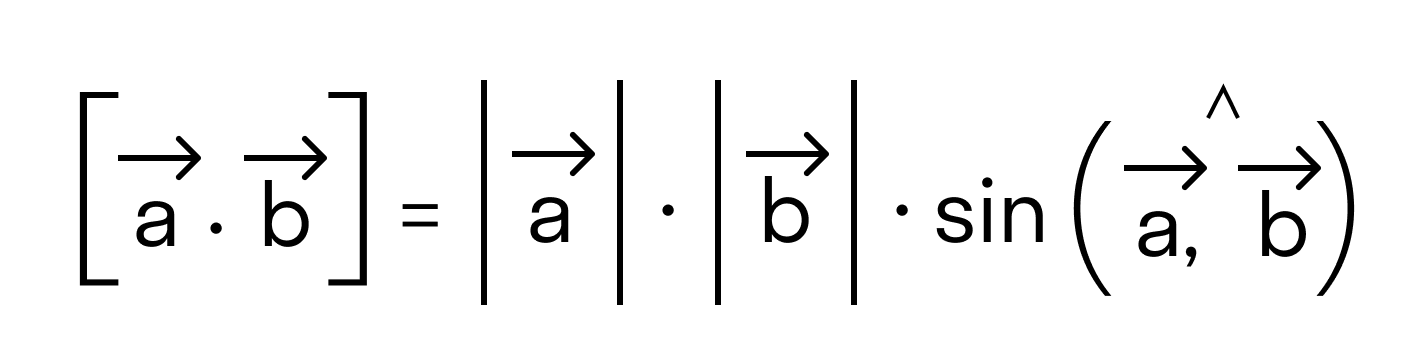
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:

Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.

Векторное произведение двух векторов a = и b = в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:

Векторное произведение векторов →a и →b обозначается как [→a • →b].

Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.

Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.

Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:

Координаты векторного произведения

Рассмотрим векторное произведение векторов в координатах.

Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.

В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор

→i, →j, →k — координатные векторы.

Это определение показывает нам векторное произведение в координатной форме.

Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:

Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:

Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.

Свойства векторного произведения

Векторное произведение в координатах представляется в виде определителя матрицы:

На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:

, где λ произвольное действительное число.

Для большей ясности докажем свойство антикоммутативности векторного произведения.

Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому

что доказывает свойство антикоммутативности векторного произведения.

Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.

Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).

Примеры решения задач

Пример 1

а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.

б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.

а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:

Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.

б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:

Пример 2

Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.

По условию снова нужно найти длину векторного произведения. Используем нашу формулу:

Согласно ассоциативным законам, выносим константы за переделы векторного произведения.

Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.

Пример 3

Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.

Сначала найдём векторы:

Затем векторное произведение:

Вычислим его длину:

Подставим данные в формулы площадей параллелограмма и треугольника:

Геометрический смысл векторного произведения

По определению длина векторного произведения векторов равна

А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.

Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.

Физический смысл векторного произведения

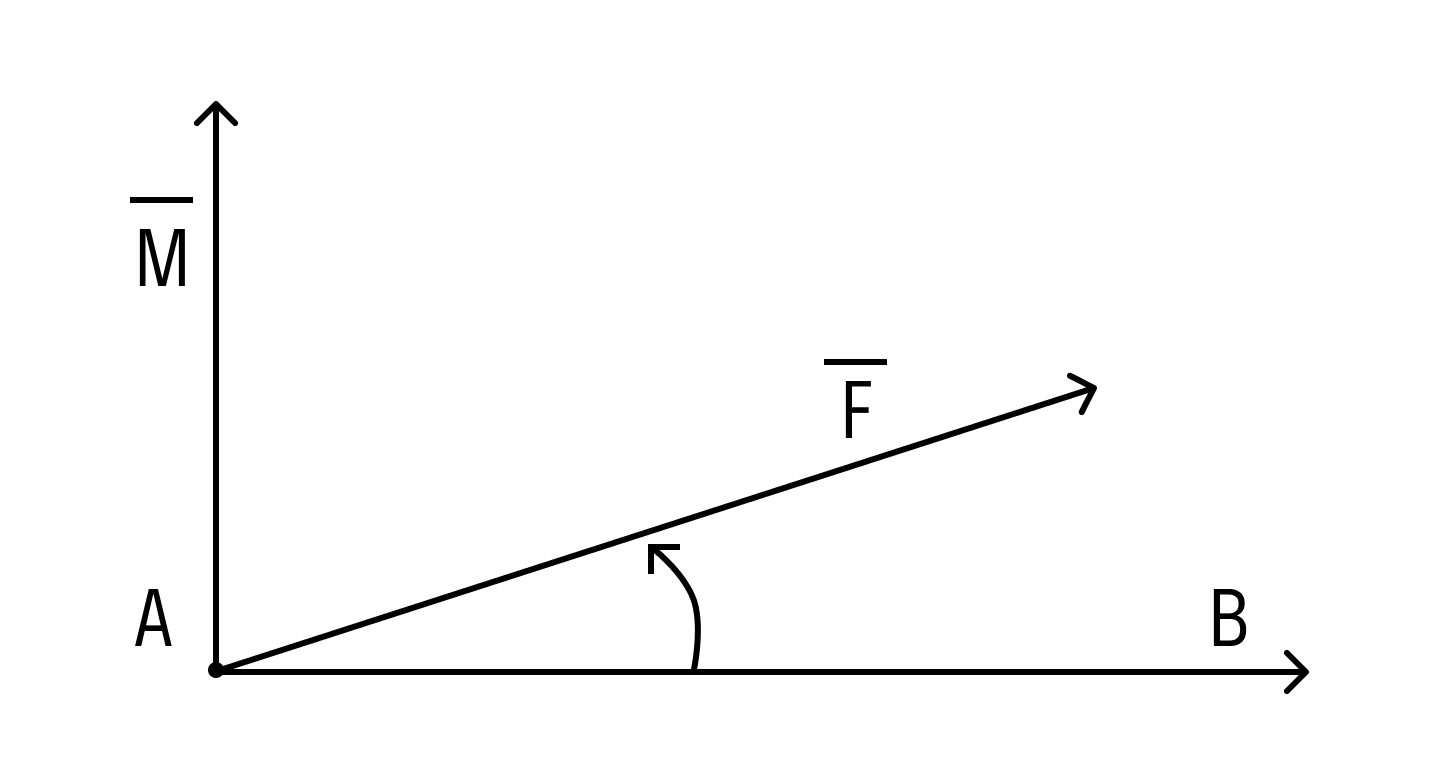
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.

Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].

Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.

Источник