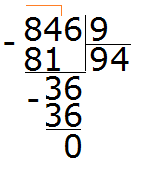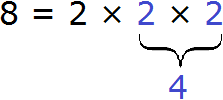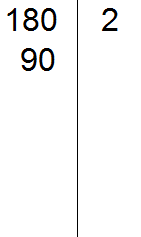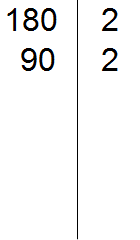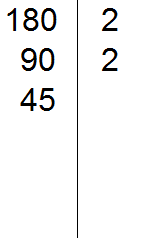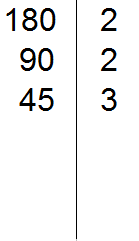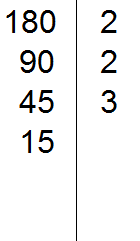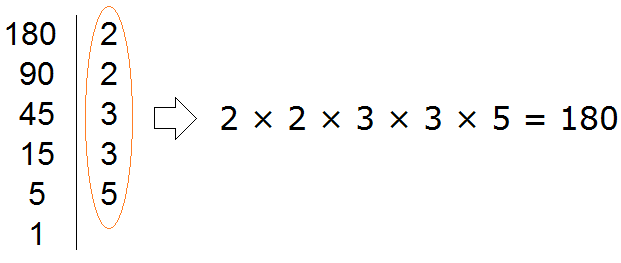Что такое некратное число в математике 6 класс

Делитель и кратное в математике

Что такое делители и кратные числа

Деление — математическое действие, которое определяет, сколько раз одно число содержится в другом. Обратной операцией является умножение.

Выделяют следующие компоненты деления:

Делимое — число, которое делят на несколько частей.

Делитель — число, которое показывает, на сколько частей нужно разделить делимое.

Частное — число, которое является результатом деления.

Умножение частного на делитель дает делимое.

Чтобы получить делитель, нужно делимое разделить на частное.

Д е л и м о е = ч а с т н о е * д е л и т е л ь Д е л и т е л ь = д е л и м о е / ч а с т н о е

Например, нужно поровну разделить 16 мандаринов между двумя детьми. Для этого 16:2=8. Таким образом, каждый ребенок получит по 8 мандаринов.

16 в этом примере является делимым, 2 — делителем, 8 — частным. Шестнадцать поделили на две части, по восемь в каждой. Или восемь содержится в 16 два раза. Или 2 содержится в 16 восемь раз. Деление прошло без остатка — нацело. Тогда число 2 является делителем числа 16.

Делителем числа a называется такое число b, на которое a делится нацело.

Например, 9 : 4 = 2 (остаток 5 ).

В примере 9 — делимое, 4 — делитель, 2 — неполное частное, 5 — остаток.

Остаток от деления — число, которое меньше делителя. Образуется при делении с остатком. Значит, в примере 9 : 4 = 2 (остаток 5 ) — число 4 не является делителем числа 9.

Задание: найдите такую пару делителей числа 144, если один из делителей равен 2.

Пусть неизвестный делитель равен x. Чтобы найти еще один делитель, если какой-то известен, нужно данное нам число разделить на известный делитель.

Тогда представим решение данной задачи в виде уравнения:

72 — целое число, без остатка.

Произведение делителей должно дать в результате 144:

72 * 2 = 144 — верно, значит, 72 — корень уравнения и делитель 144.

Ответ: числа 2 и 72 — делители 144.

Число называют кратным, если оно делится на данное число нацело, без остатка.

Например, 15:3 нацело.

Тогда число 15 является кратным 3.

Слово «кратно» синонимично слову «делится».

Фразу «15 кратно 3» можно в уме заменить на «15 делится на 3 нацело».

Основные понятия и определения

Делитель — это число, на которое данное число делится нацело. Делитель всегда меньше или равен числу.

Делится нацело = без остатка.

Наименьшим делителем любого числа является единица.

Наибольшим делителем числа является само число.

Делителем нуля будет любое число, но сам 0 делителем не будет.

При делении нуля на любое число получаем 0. А делить на ноль нельзя.

У единицы только один делитель — единица.

Другие числа, кроме 1, имеют не меньше двух делителей.

Кратное — число, которое делится на данное число нацело. Всегда больше или равно числу.

Наименьшее кратное числа является равным самому числу.

Наибольшее кратное подобрать нельзя, потому что ряд натуральных чисел бесконечен. У любого натурального числа бесконечное множество кратных.

Ноль является кратным для любого числа. При умножении на ноль всегда получается ноль.

Когда одно число делится нацело на другое, то первое число — кратное второго, а второе — делитель первого.

Чем отличаются друг от друга, как найти

Делитель отличается от кратного тем, что:

Чтобы найти делители числа, нужно данное число разложить на множители.

Разложить на множители — представить число в виде произведения целых чисел.

Чтобы проверить, является ли одно число делителем другого, нужно разделить число на данное нам.

Для нахождения кратного числа заданному числу, нужно это число последовательно умножать на натуральные числа. Каждое полученное число будет кратно — будет делиться — заданному.

Делители и кратные связаны между собой. Например, делителем числа 15 является 3 и число, кратное 3, равно 15.

Примеры решения задач

Необходимо найти делители числа 14.

Решить задание можно двумя способами.

Последовательно делим 14 на натуральные числа от 1 до 14. Помним, что делитель всегда меньше или равен заданному числу.

Выбираем такие числа в качестве делителя, при делении на которые мы не получили остаток: 1, 2, 7, 14.

Ответ: делители числа 14: 1, 2, 7, 14.

Представим 14 в виде произведения чисел:

Делителями будут множители, так как можем разделить 14 нацело на каждый из них.

Ответ: делители 14: 1, 2, 7, 14.

Найдите три числа, кратных 7.

Чтобы найти число, кратное данному, нужно это число умножить на любое натуральное число.

7 * 1 = 7 — семь кратно семи;

7 * 2 = 14 — 14 кратно 7;

7 * 3 = 21 — 21 кратно 7.

Ответ: числа, кратные 7: 7, 14, 21.

Самостоятельно проверьте, 225 кратно 3 или нет.

Чтобы проверить, кратно ли одно число другому, нужно разделить числа друг на друга.

75 — целое число, при делении нет остатка. Тогда 225 кратно 3.

Найдите любое число, делителями которого являются числа 7 и 8.

Самый простой способ, если в задании не оговорены еще какие-либо условия, просто перемножить эти делители:

Источник

Что такое кратное число

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, что такое КРАТНЫЕ ЧИСЛА.

Эту тему каждый школьник в России проходит в 6 классе, когда подробно изучают деление.

Хотя с самой этой математической функцией дети знакомятся гораздо раньше – уже во 2 классе.

Деление – это математическая операция, благодаря которой можно узнать, сколько частей чего-то одного содержится в другом. Или, другими словами, заменяет многократное вычитание из одного числа другое.

Операция деления в математике может обозначаться разными значками. Это двоеточие (:), косая черта (/), горизонтальная черта (-) или специальным значком под названием «обелюс» (÷).

А у чисел, которые участвуют в делении, есть определенные названия:

Частное, которое получается полным или не полным. Первый вариант, это когда число-делимое, было полностью поделено на делитель. Например, 12 / 3 = 4. Но бывают варианты и с неполным частным, когда появляется некий остаток. Например, 14 / 3 = 4 (2), где 4 – это неполное частное, а 2 – остаток.

Почему мы так подробно рассказали о делении? Это имеет непосредственное отношение к теме статьи.

Одно число называется кратным другому, если его можно на него поделить без остатка.

Но речь идет только о натуральных числах. То есть тех, которые мы используем для счета в обычной жизни. Например, 1, 2, 5, 10, 35, 100 и так далее. При этом дробные числа (например, 2/5 или 0,5) к натуральным не относятся, а значит, в отношении них понятие «кратности» не применяется.

Например, возьмем число 12. Оно может быть кратно сразу нескольким числам.

12 / 3 = 4
12 / 4 = 3
12 / 6 = 2
12 / 2 = 6

Таким образом, можно сказать, что 12 – кратное число 2, 3, 4 и 6. И точно так же можно разложить по кратности любое число.

Внимательный читатель мог бы возразить, что есть еще два числа, на которые можно поделить 12 без остатка. Во-первых, это само 12. А во-вторых, это единица. Что ж, это абсолютная правда, и ее можно даже записать в одном математическом правиле:

Любое натуральное число всегда кратно само себе и единице. В первом случае получается единица, а во втором само число.

Таблицы чисел кратных 2,3,4,5,6,7,9

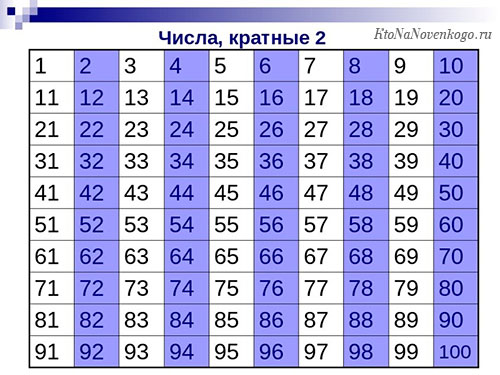
В первую очередь рассмотрим самый простой вариант. Это числа, которые являются кратными двум. Определить их совсем просто, так как к ним относятся все четные числа. Вот, например, как выглядит таблица от 1 до 100.

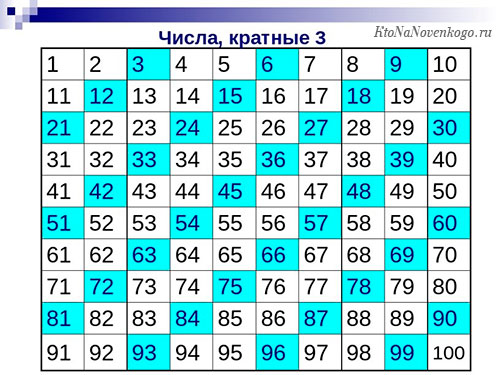
А вот так будет выглядеть таблица чисел кратных трем. Обратите внимание, что все они в результате располагаются по диагонали. Получается весьма красиво.

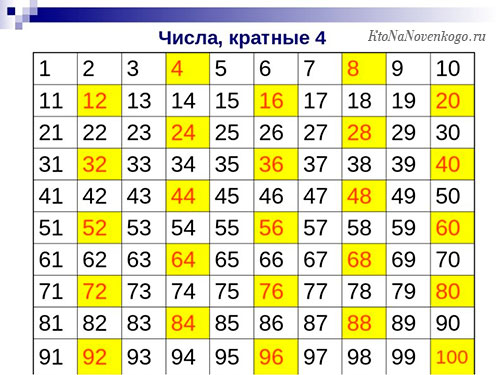
Теперь покажем таблицу чисел, которые можно поделить без остатка на 4. Как можно заметить, это только четные цифры.

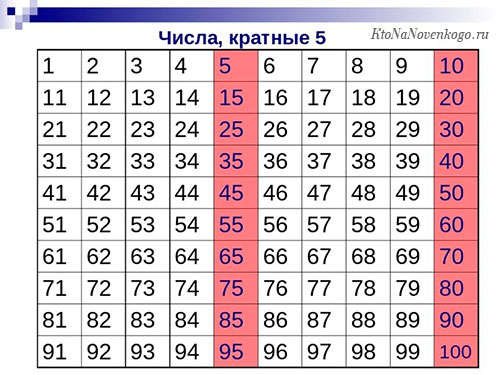
А вот так выглядит таблица чисел, которые кратны пяти. Запомнить их очень просто. Числа, кратные пяти, должны оканчиваться или на 5, или на 0. Других вариантов быть просто не может.

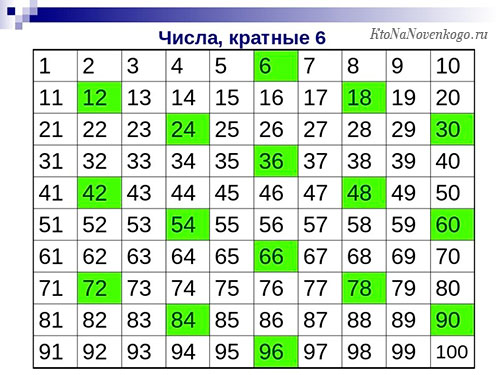
А если взглянуть на таблицу чисел, которые кратны числу 6, то можно сделать интересный вывод. Есть числа, которые никогда не попадут в эту категорию. Они оканчиваются на 1, 3, 5, 7 и 9. Другими словами, только четные числа могут быть кратными 6. Но при этом не все четные числа таковыми являются.

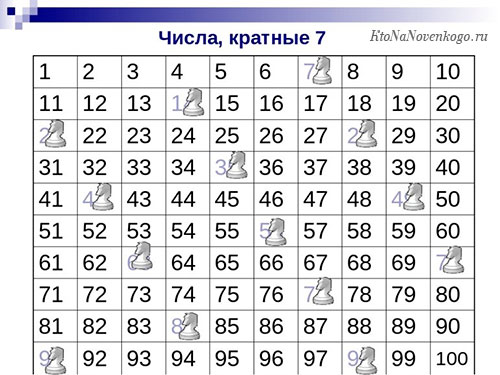
Интересно будет посмотреть и таблицу чисел, которые являются кратными 7. Чтобы определить их, нужно ходить по таблице вниз, как ходить шахматная фигура «конь». В народе это называется «буквой Г», в нашем случае это «шаг влево и два шага вниз».

И наконец, интересно рассмотреть числа, которые кратны 9. Их очень легко определить, это своеобразный математический лайфхак.

Надо просто сложить все цифры в числе, и если в сумме получится 9, то тогда число кратно девятке.

Да, тут указаны еще и числа 18 и 27. Но они при повторном сложении также дадут девятку.

Вместо заключения

А знаете, что есть число, которое можно назвать кратным всем другим натуральным числам? Это ноль. Ведь если ноль поделить на любое число, то получится опять же ноль. И никакого остатка. А значит, это утверждение верно.

Вот и все, что мы хотели рассказать о КРАТНЫХ ЧИСЛАХ.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Тут надо запомнить всего лишь одно, то что число должно делиться без остатка, а дальше все будет просто и для этого даже никакой таблицы не надо.

Но кстати за таблицы все равно спасибо. Сейчас моя как раз в школе проходит, и распечатал ей, чтобы было просто понятнее. Не знаю, нас как то лучше обучали что ли. У меня эта тема вообще в школе трудностей никаких не вызвала, а современные школьники вообще не понимают что это такое.

Источник

Публикации: Математика, алгебра

Совокупность всех этапов развития любой науки представляет собой длительную последовательность эвристических догадок, которые не являются знанием в полном смысле этого понятия, а всего лишь образуют в нашем воображении некоторое приближенное представление о реальной действительности.

Новые представления об окружающей нас действительности не может вывести логически ни одна наука. Только эвристические догадки позволяют получать новые представления об окружающем нас материальном мире. Каждое новое представление полученное с помощью эвристических догадок заведомо не соответствует реальной действительности.

• Mathematics, Solution of topical problems of number theory, article [word], Mykhaylo Khusid, 13.01.2021
It is known that an even number can be represented by the sum of six, four
simple. In this work, the author proves by equating these
the sum that they are equivalent, the sum of four and two primes, which allows us to solve the binary Goldbach-Euler hypothesis, and that
solves the second problem of infinity of twin primes.
The author is grateful to those who studied his article and pointed out errors.

Автор предлагает решение проблемы. Считает, что нашёл упрощённое решение. Признателен специалистам, заинтересовавшимися данной работой и высказавшим своё независимое мнение.

Автор предлагает алгебраическое решение широко известной теоремы Ферма. Он использует методы доступные широкому кругу
читателей. Будет признателен рецензиям специалистов.

Автор нашёл алгебраическое решение одной из популярнейших
задач в теории чисел теоремы Ферма. Автор использует методы,
доступные самому широкому кругу читателей. Будет признателен,откликнувшимся на статью.

Автор считает,что нашёл алгебраический вариант доказательства.Автор использует методы элементарной математики,что может быть доступно самому широкому кругу читателей. Автор будет признателен специалистам,откликнувшимся
на статью.

where on the left is the sum of three odd primes

In this article, the author gives a proof of Theorem 1 using

Goldbach’s problem is that

where on the right sum of four prime numbers, at the left any even number,

since 12, by method of mathematical induction.

Keywords: and on this basis decides topical number theory problems.

известно, что окончательно решена слабая проблема
Гольдбаха. p1 + p2 + p3 = 2N+1 [1]
где слева сумма трёх простых чисел, справа нечётные числа, начиная с 9
В данной работе автор приводит доказательство теоремы1, опираясь на решение слабой проблемы Гольдбаха, что: p1 + p2 + p3 + p4 = 2N [2]
где справа сумма четырёх простых чисел, слева любое чётное число,
начиная с 12,
методом математической индукции.

В статье приведены результаты эмпирических исследований составных чисел Мерсенна: определены наименьшие простые делители составных чисел Мерсенна; дана оценка относительного числа составных чисел Мерсенна, простые делители которых определены. Общее число рассмотренных чисел Мерсенна составляет 400.

Аннотация: Представлено теоретическое и экспериментальное обоснование использования метода остаточного расширения для оценки статической прочности цилиндрических стальных баллонов. Используются единая кривая деформирования и деформационная теория пластичности. Приведена возможность обоснованного назначения предельно-допустимого коэффициента остаточного расширения, используемого при периодической инспекции баллонов.
Ключевые слова: стальные баллоны, гидроиспытания внутренним давлением, изменение объема, запас прочности, периодическая проверка.

В статье приведены результаты эмпирических исследований составных чисел Мерсенна: определены наименьшие простые делители составных чисел Мерсенна; дана оценка относительного
числа составных чисел Мерсенна, простые делители которых определены. Общее число рассмотренных чисел Мерсенна составляет 400.

В статье приведено описание метода факторизации чисел Мерсенна. Метод разработан на основе алгебраических операций
умножения и деления на множестве Bp. Элементы множества имеют
вид 2pn+1, n=1,2,3. где p-индекс числа Мерсенна Mp.

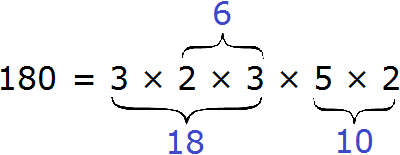
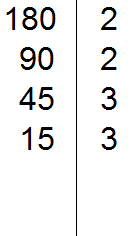
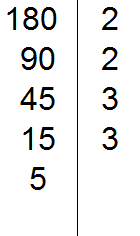
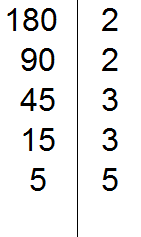
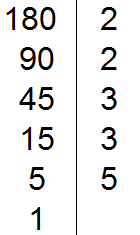
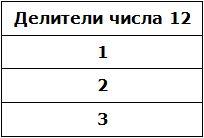
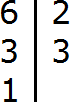
В статье приведено описание метода факторизации чисел Мерсенна. Разработан на основе алгебраических операций
умножения и деления на множестве
Bp=

В статье приведено описание метода факторизации чисел
Мерсенна, разработанного на основе алгебраических операций
умножения и деления на множестве Bp=

Число 2 выглядит белой вороной среди простых чисел. 2 – единственное чётное простое число, все остальные простые числа нечётны. Но ведь и 3 – единственное простое число кратное трём, все остальные не кратны 3-м. Более того, все простые, кроме 2 и 3, некратны 2 и 3.

Источник

Делители и кратные

В данном уроке мы рассмотрим такие понятия как делители и кратные.

Что такое делитель?

Мы знаем, что делитель это число, показывающее на сколько частей нужно разделить делимое. Например, в выражении 8 : 2 = 4, делителем является число 2. Это число показывает на сколько частей нужно разделить число 8. После разделения получается ответ 4. Как видно из примера, число 8 делится на число 2 без остатка. Говорят, что число 2 является делителем числа 8.

Пример 1. Число 2 является делителем числа 8, поскольку 8 делится на 2 без остатка:

Пример 2. Число 3 является делителем числа 9, поскольку 9 делится на 3 без остатка:

Пример 3. Число 4 не является делителем числа 10 поскольку 10 не делится на 4 без остатка:

10 : 4 = 2 (2 в остатке)

Определение. Делителем числа а называется число, на которое число а делится без остатка.

Делителем числа 12 называется число, на которое 12 делится без остатка.

Попробуем перечислить эти числа:

Все эти числа являются делителями числа 12, поскольку число 12 делится на них без остатка. Покажем это:

12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 12 = 1

Кратные числа

Если какое-нибудь число без остатка разделилось на другое, то его называют кратным этого числа. Например, 6 без остатка делится на 3. Поэтому 6 является кратным числа 3

Определение. Кратным числа а называется число, которое делится без остатка на а.

Кратным числа 5 называется число, которое делится без остатка на 5 .

У любого числа бесконечно много кратных. Например, первыми кратными числа 5, являются числа 5, 10, 15, 20, 25. Все они кратны 5, поскольку делятся на 5 без остатка:

5 : 5 = 1
10 : 5 = 2
15 : 5 = 3
20 : 5 = 4
25 : 5 = 5

Признаки делимости чисел

Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.

Признак делимости на 10

Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.

Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.

В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.

Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.

Признак делимости на 5 и на 2

Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.

Признак делимости на 5

Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.

Признак делимости на 3

Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:

Признак делимости на 9

Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9

Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:

Чётные и нечётные числа

Чётным называется число, которое делится без остатка на 2. Например, число 20 является четным, поскольку оно делится без остатка на 2:

Нечётным называется число, если при его делении на 2, остаётся остаток 1. Например число 21 является нечетным, поскольку после его деления на 2 остается остаток 1:

21 : 2 = 10 (1 в остатке)

Как распознать чётное число от нечетного, не выполняя деления на 2? Очень просто. Из однозначных чисел чётными являются числа 0, 2, 4, 6, 8, а нечетными являются 1, 3, 5, 7, 9. Если число оканчивается чётной цифрой, то это число является чётным. Если число оканчивается нечетной цифрой, то это число является нечетным.

Например, число 308 чётно, поскольку оно оканчивается чётной цифрой. Число 1024 тоже четно, поскольку оканчивается четной цифрой.

А числа 305 и 1027 являются нечётными, поскольку они оканчиваются нечётными цифрами.

Простые и составные числа

Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:

Значит, число 5 является простым числом.

Составным же называется число, которое имеет два и более делителя. Например, число 4 составное, поскольку у него два и более делителя: 4, 2 и 1

Значит, число 4 является составным числом.

Разложение составного числа на простые множители

Любое составное число можно разложить на простые множители. Чем-то похожим мы занимались в уроке замены в выражениях. Из этого урока мы узнали, что любое число, входящее в выражение, можно заменить на то же самое, но записанное в другом виде.

Суть разложения числа на простые множители заключается в том, чтобы представить это число в виде произведения нескольких простых множителей.

Разложим число 4 на простые множители. Для этого соберем данное число из других чисел, при этом соединим их знаком умножения (×). Число 4 состоит из чисел 2 и 2. Эти два числа и являются простыми множителями, из которых состоит число 4

Разложим на множители число 6. Число 6 можно собрать из чисел 2 и 3. Эти два числа и являются простыми множителями, из которых состоит число 6

Большие числа раскладываются таким же образом. Сначала их раскладывают на большие множители, затем эти большие множители раскладывают на маленькие. И так до тех пор, пока каждый множитель не станет простым числом.

Например, разложим число 180 на простые множители. Число 180 это два множителя 18 и 10

Теперь раскладываем множители 18 и 10 на другие множители:

Теперь раскладываем выделенную синюю шестерку. Это последний большой множитель, который можно разложить на простые множители:

Теперь собираем все простые множители вместе:

На множители можно разложить только составное число. Простое число на множители не раскладывается. Именно поэтому, когда разложение доходит до простых чисел, мы эти простые числа дальше не раскладываем.

Есть и второй способ разложения на простые множители. Он проще и хорошо подходит для больших чисел. Суть этого способа заключается в том, что сначала проводится вертикальная линия. Затем слева от этой линии записываются делимые, а справа — делители, которые впоследствии собирают во множители.

При разложении числа этим способом, используют признаки делимости, такие как: признаки делимости на 2, на 3, на 5 и другие.

Например, разложим предыдущее число 180 этим способом.

Проводим вертикальную линию и слева записываем первое делимое 180

Теперь применяем признаки делимости. В первую очередь проверяем делится ли 180 на 2. Если делится, то нужно записать эту двойку справа от вертикальной линии.

180 делится на 2, поскольку 180 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 180 на 2 и получаем второе делимое 90. Записываем это делимое слева от вертикальной линии:

Теперь делим 90. Снова применяем признаки делимости. Проверяем делится ли 90 на 2.

90 делится на 2, поскольку 90 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 90 на 2, получаем третье делимое 45. Записываем это делимое слева от вертикальной линии:

Теперь делим 45. Снова применяем признаки делимости. Проверяем делится ли 45 на 2.

45 на 2 не делится. Тогда проверяем делится ли 45 на 3.

45 делится на 3, поскольку сумма цифр 4 и 5 делится на 3. Записываем тройку справа от вертикальной линии:

Делим 45 на 3, получаем четвёртое делимое 15. Записываем это делимое слева от вертикальной линии:

Теперь делим 15. Проверяем делится ли 15 на 2.

15 не делится на 2. Тогда проверяем делится ли 15 на 3.

15 на 3 делится, поскольку сумма цифр 1 и 5 делится на 3. Записываем тройку справа от вертикальной линии:

Делим 15 на 3, получаем пятое делимое 5. Записываем пятёрку слева от вертикальной линии:

Теперь делим 5. Проверяем делится ли 5 на 2.

5 не делится на 2. Тогда проверяем делится ли 5 на 3.

5 не делится на 3. Тогда проверяем делится ли 5 на 5.

5 делится на 5. Записываем эту пятёрку справа от вертикальной линии:

Делим 5 на 5, получаем шестое делимое 1. Записываем эту единицу слева от вертикальной линии:

На этом деление завершается, поскольку мы достигли единицы. Делители, которые записывают справа от вертикальной линии должны быть простыми числами. Поэтому, когда делимое 5 не разделилось на 2, а затем не разделилось на 3, мы попробовали разделить его на 5, не пробуя разделить на 4, поскольку 4 является не простым, а составным числом.

Теперь переписываем в один ряд все делители, которые записаны справа от вертикальной линии. Они и будут разложением числа 180 на простые множители. Желательно записывать их, начиная с самых малых. Это позволяет упорядочить их по возрастанию:

Не расстраивайтесь, если будете испытывать затруднения при разложении чисел на простые множители. Эта тема требует немного практики. Для тренировки можете разложить на простые множители следующие числа: 256, 378, 512.

Нахождение делителей числа

В начале данного урока было сказано, что делителем называется число, на которое другое число делится без остатка.

Например, число 2 является делителем числа 6, поскольку число 6 можно без остатка разделить на 2

6 : 2 = 3

Ещё делителем числа 6 является число 3

6 : 3 = 2

Ещё делителем числа 6 является число 1

6 : 1 = 6

Наконец, делителем числа 6 является само это число

6 : 6 = 1

Перечислим все делители числа 6

1, 2, 3, 6

Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим несколько примеров.

Пример 1. Найти делители числа 12

Во-первых, единица является делителем любого числа. Пусть и у нас первым делителем числа 12 будет 1

Теперь раскладываем число 12 на простые множители:

Получили разложение 2 × 2 × 3.

В процессе разложения числа 12 на простые множители, мы делили его на числа 2 и 3. На них число 12 разделилось без остатка, значит они тоже являются делителями числа 12. Внесём эти два числа в нашу таблицу делителей:

Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой. Получаемые в результате ответы и будут остальными делителями числа 12.

Число 12 мы разложили на простые множители 2 × 2 × 3. Найдём все возможные произведения этих простых множителей между собой. Первое произведение это 2 × 2. Это произведение равно 4

Занесём число 4 в нашу таблицу делителей

Следующее возможное произведение из простых множителей числа 12 это произведение 2 × 3. Данное произведение равно 6. Занесём число 6 в нашу таблицу делителей:

Последнее возможное произведение из простых множителей числа 12 это произведение из всех его множителей, а именно 2 × 2 × 3. Это произведение равно 12. Занесём число 12 в нашу таблицу делителей:

Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.

На основании приведённого примера можно сформировать правило для нахождения делителей числа:

Чтобы найти делители числа, нужно:

Пример 2. Найти делители числа 6

Первым делителем числа 6 запишем единицу:

Теперь разложим число 6 на простые множители:

Выпишем из полученного разложения те множители, которые являются делителями числа 6. Видим, что это множители 2 и 3. Они будут следующими делителями числа 6. Допишем их к нашим делителям:

1, 2, 3

1, 2, 3, 6

Источник