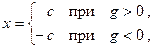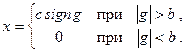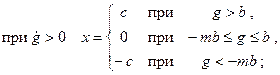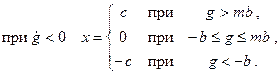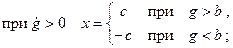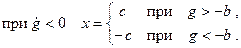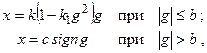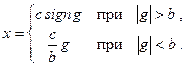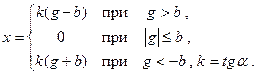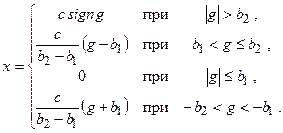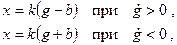Что такое нелинейная система

Нелинейная система

Нелинейная система — динамическая система, в которой протекают процессы, описываемые нелинейными дифференциальными уравнениями.

Свойства и характеристики нелинейных систем зависят от их состояния. Некоторые виды нелинейных звеньев:

В отличие от линейной системы не обладает свойствами суперпозиции, частота выходного сигнала зависит от его амплитуды и др.

Многие нелинейные системы в области малых изменений параметров поддаются линеаризации.

Примеры

См. также

Полезное

Смотреть что такое «Нелинейная система» в других словарях:

нелинейная система — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] нелинейная система Система, которая характеризуется тем, что все или некоторые преобразования, связывающие входные … Справочник технического переводчика

Нелинейная система — [nonli­ne­ar system] система, которая характеризуется тем, что все или некоторые преобразования, связывающие входные величины, параметры состояний и выходные величины, являются нелинейными, т.е. не удовлетворяют условиям линейности (см. Линейная… … Экономико-математический словарь

нелинейная система — netiesinė sistema statusas T sritis automatika atitikmenys: angl. non linear system vok. nichtlineares System, n rus. нелинейная система, f pranc. système non linéaire, m … Automatikos terminų žodynas

нелинейная система — netiesinė sistema statusas T sritis fizika atitikmenys: angl. non linear system vok. nichtlineares System, n rus. нелинейная система, f pranc. système non linéaire, m … Fizikos terminų žodynas

геометрически нелинейная система — Система, у которой нелинейная зависимость между перемещениями и силами обусловлена только характером взаимного расположения и соединения элементов. [Сборник рекомендуемых терминов. Выпуск 82. Строительная механика. Академия наук СССР. Комитет… … Справочник технического переводчика

физически нелинейная система — Система, у которой нелинейная зависимость между перемещениями и силами обусловлена нелинейной зависимостью между деформациями и напряжениями материала. [Сборник рекомендуемых терминов. Выпуск 82. Строительная механика. Академия наук СССР. Комитет … Справочник технического переводчика

Геометрически нелинейная система — Геометрически нелинейная система – система, у которой нелинейная зависимость между перемещениями и силами обусловлена только характером взаимного расположения и соединения элементов. [Отраслевой руководящий документ. Техническая… … Энциклопедия терминов, определений и пояснений строительных материалов

система — Группа взаимодействующих объектов, выполняющих общую функциональную задачу. В ее основе лежит некоторый механизм связи. [ГОСТ Р МЭК 61850 5 2011] система Набор элементов, которые взаимодействуют в соответствии с проектом, в котором элементом… … Справочник технического переводчика

Система — [system] множество элементов, находящихся в отношениях и связях друг с другом, которое образует определенную целостность, единство. Следует отметить, что это определение (взятое нами из Большой Советской Энциклопедии) не является ни единственным … Экономико-математический словарь

НЕЛИНЕЙНАЯ ОПТИКА — раздел оптики, охватывающий исследования распространения мощных световых пучков в тв. телах, жидкостях и газах и их вз ствия с в вом. Сильное световое поле изменяет оптич. хар ки среды (показатель преломления, коэфф. поглощения), к рые становятся … Физическая энциклопедия

Источник

Общие понятия и особенности нелинейных систем

Строго говоря, линейных систем в природе не существует, так как характеристики реальных устройств нелинейные и некоторые из них не могут быть линеаризованы, например, характеристика логического элемента. Кроме того, есть системы, например, релейные, адаптивные, в которых принципиально необходимо учитывать нелинейности.

Нелинейной системой называется такая система, в состав которой входит хотя бы одно звено, описываемое нелинейным уравнением. Такое звено называется нелинейным звеном или нелинейным элементом.

Уравнение является нелинейным, если некоторые координаты или их производные по времени входят в уравнение в виде произведений или степени, отличной от первой, а также если коэффициенты уравнения являются функциями некоторых координат или их производных.

При составлении дифференциальных уравнений нелинейных систем сначала составляют дифференциальные уравнения для каждого устройства системы. При этом характеристики устройств, допускающих линеаризацию, линеаризуются. В результате получают систему дифференциальных уравнений, в которой одно или несколько уравнений нелинейные. Устройства, допускающие линеаризацию, образуют линейную часть системы, а устройства, которые не могут быть линеаризованы, составляют нелинейную часть.

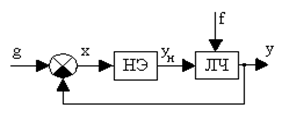
Путем эквивалентного преобразования структурных схем и нелинейных звеньев большое число нелинейных систем можно представить в виде замкнутого контура с последовательным включением нелинейного элемента (НЭ) и линейной части (ЛЧ), как показано на рис. 2.1.

Рис. 2.1. Функциональная схема нелинейной системы:

Классификация нелинейных элементов и систем. Нелинейные звенья классифицируются по различным признакам. Наибольшее распространение получила классификация по статическим и динамическим характеристикам, так как в системах чаще всего нелинейности приходится учитывать в виде характеристик. Эти характеристики могут быть как однозначными, так и двузначными (петлевыми), симметричными и несимметричными относительно начала координат.

Различают следующие основные типы нелинейных звеньев.

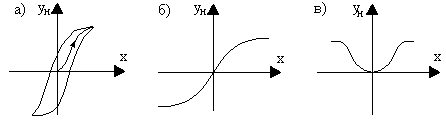
Нелинейные звенья с гладкими криволинейными характеристиками. Примеры таких характеристик приведены на рис. 2.2.

Рис. 2.2. Гладкие криволинейные характеристики:

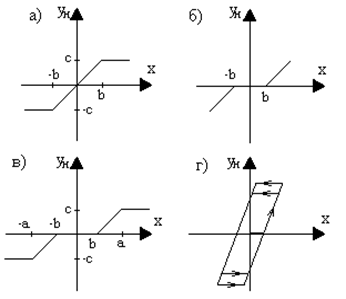
Нелинейные звенья с кусочно-линейными характеристиками. Некоторые из таких характеристик представлены на рис. 2.3.

Рис. 2.3. Кусочно-линейные характеристики:

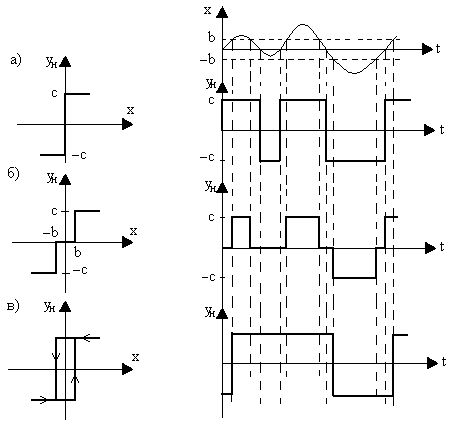
Рис. 2.4. Релейные характеристики:

Кроме того, на рис. 2.4 показано прохождение непрерывного сигнала через соответствующие типы реле. Откуда следует, что коэффициент передачи реле зависит от величины входного воздействия.

Для улучшения динамических свойств систем специально созданы нелинейные звенья с опережающими двузначными статическими характеристиками.

Часто встречаются элементы с несимметричными относительно начала координат статическими характеристиками.

Нелинейные вычислительные звенья, например, множительное, логическое звено и другие.

Нелинейные системы обычно классифицируются в соответствии с видом входящих в них нелинейных звеньев.

Особенности нелинейных систем. Поведение нелинейных систем, при наличии существенных нелинейностей, значительно отличается от поведения их линейных моделей [10].

1. Выходная величина нелинейной системы непропорциональна входному воздействию; форма реакции системы зависит от величины входного воздействия.

2. Характер процессов в нелинейной системе зависит от величины начального отклонения, вызванного возмущением. В связи с этим для нелинейных систем существуют понятия об устойчивости “в малом”, “в большом”, “в целом”.

Система устойчива “в малом”, если она устойчива при малых (бесконечно малых) начальных отклонениях. Система устойчива “в большом”, если она устойчива при больших (конечных по величине) начальных отклонениях. Система устойчива “в целом”, если она устойчива при любых больших (неограниченных по величине) начальных отклонениях.

3. Для нелинейных систем характерен режим незатухающих периодических колебаний с постоянной амплитудой и частотой (автоколебаний), возникающий в системах при отсутствии периодических внешних воздействий.

4. При затухающих колебаниях переходного процесса в нелинейных системах происходит изменение периода колебаний.

Основные задачи исследования нелинейных систем. Методы исследования. Задачами исследования нелинейных систем являются:

1) отыскание возможных состояний равновесия системы и исследование их устойчивости;

2) определение автоколебаний и анализ их устойчивости;

3) исследование процессов перехода системы к тому или иному установившемуся состоянию при различных начальных отклонениях.

Начало исследования нелинейных систем обычно связано с рассмотрением устойчивости и определением автоколебаний.

В настоящее время не создано общей теории анализа нелинейных систем. Разработанные методы позволяют решать лишь отдельные нелинейные задачи.

Все инженерные методы исследования нелинейных систем разделяются на две основные группы.

Точные методы, например, метод А.М.Ляпунова, метод фазовой плоскости, метод точечных преобразований, частотный метод В.М.Попова, основаны на точном решении нелинейного дифференциального уравнения, может быть и упрощенного.

Приближенные методы, такие как метод гармонической линеаризации, метод статистической линеаризации, основаны на линеаризации нелинейного уравнения системы.

Мощным и эффективным методом исследования нелинейных систем является моделирование, инструментарием которого служит компьютер. В настоящее время многие сложные для аналитического решения теоретические и практические вопросы сравнительно легко могут быть решены с помощью вычислительной техники.

Источник

Общая характеристика нелинейных систем

1. Определение нелинейной системы

К нелинейным системам относятся все системы, которые не могут быть описаны линейными дифференциальными уравнениями. Нелинейные системы очень многообразны, поэтому практически нельзя говорить о едином “классе” нелинейных систем, противостоящем классу линейных систем. Исследование нелинейных систем связано с преодолением значительных математических трудностей. Основная трудность состоит в том, что не существует единого точного метода решения нелинейных уравнений и для каждого вида нелинейности приходится изыскивать специфический частный метод.

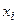
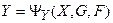
Для описания системы автоматического управления могут быть всегда выбраны такие n координат состояния объекта , при которых уравнения, описывающие процессы в системе, принимают вид

, (22.1)

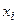
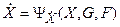
где вектор состояния X с координатами задается системой дифференциальных уравнений первого порядка в матричной форме

(22.2)

Здесь вектор Y выражает m управляемых переменных, вектор G выражает l задающих воздействий, а вектор F – соответственно k внешних воздействий.

Если рассматривать систему при детерминированных воздействиях, то есть внешние воздействия G и F являются известными функциями времени t, то в этом случае уравнения (22.1) и (22.2) примут вид:

, (22.3)

. (22.4)

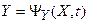
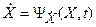
Уравнение (22.4) – это матричная запись n нелинейных дифференциальных уравнений первого порядка рассматриваемой системы порядка n:

. (22.5)

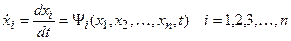
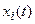
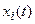
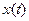
В матричном описании САУ весьма существенен рациональный выбор координат состояния, описывающих систему. Обычно руководствуются соображениями простоты уравнения (22.3), выражающего управляемую величину через координаты состояния и стремлением не иметь разрывов в функциях . Решение системы уравнений (22.5) при заданных начальных условиях дает возможность для каждой координаты состояния определить описывающую ее функцию времени , а процесс, наблюдаемый в системе, изобразить в виде линии в n – мерном пространстве координат состояния, для которого время t является параметром точки кривой, соответствующей уравнению .

Изображение процесса в пространстве состояний дает возможность наглядно проследить изменение всех координат состояния на любом интервале t от 0 до ¥.

Уравнения (22.5) охватывают широкий класс систем, хотя, конечно, и не исчерпывают всего их многообразия. Существенный интерес представляет класс систем, когда система уравнения состоит из ряда линейных элементов и связей, объединенных в одну линейную часть (ЛЧ) и одного нелинейного элемента. В этом случае дифференциальные уравнения системы могут быть записаны следующим образом:

(22.6)

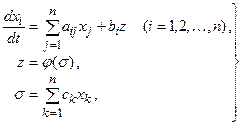
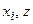
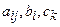
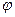
где — координаты;

— постоянные вещественные коэффициенты;

— нелинейная функция.

Система (22.6) интересна тем, что целый ряд практических систем управления одной величины может быть сведен к данной схеме. В дальнейшем ограничимся рассмотрением в основном нелинейных систем, уравнения которых могут быть приведены к виду (22.5) и к виду (22.6). Для этих систем характерно то, что исходная система уравнений может быть разрешена относительно первых производных всех координат по времени и, таким образом, приведена к виду, где под знаком нелинейной функции стоят только сами переменные, но не их производные.

Математический аппарат анализа нелинейных систем связан с необходимостью исследования нелинейных дифференциальных уравнений, теория которых содержит множество индивидуальных методов, присущих различным видам уравнений, описывающих систему. Сложность решения нелинейных дифференциальных уравнений вызывает необходимость создания ряда приближенных методов, позволяющих судить о характере процессов, наблюдаемых в системе. При этом нелинейные характеристики реальных элементов системы заменяют некоторыми идеализированными приближенными характеристиками, которые обусловлены как характером нелинейного элемента, так и принятым методом анализа системы.

Методы анализа и синтеза нелинейных САУ весьма разнообразны и выбор того или иного метода зависит от постановки задачи исследования, вида нелинейности и порядка дифференциального уравнения, описывающего систему.

Для решения нелинейных уравнений, кроме аналитических и графических методов, широко применяют методы моделирования с помощью аналоговой вычислительной техники (АВМ) и численного решения задач с помощью цифровых вычислительных машин (ЦВМ).

Простота моделирования нелинейных звеньев, наглядность получаемых решений фиксируемых обычно на осциллографе или самопишущих приборах, легкость изменения различных параметров моделируемой системы – все это обеспечило массовое применение АВМ для анализа и синтеза нелинейных систем управления.

Несмотря на большие трудности исследования нелинейных систем, интерес к ним за последнее время резко возрос. Это объясняется в частности, тем, что по показателям качества процесса регулирования (быстродействие, точность) нелинейные системы очень часто превосходят соответствующие линейные системы. Это относится к таким системам, в которые целенаправленно вводятся специальные нелинейности, определяющие эффективность динамических процессов.

Выдающаяся роль в создании и развитии методов исследования нелинейных систем принадлежит русским ученым. Наиболее важный вклад в эту область бал сделан А.М.Ляпуновым, опубликовавшим в 1892 году свою работу “Общая задача об устойчивости движения”. В этой работе было впервые дано определение понятия устойчивости движения и разработаны методы решения этой задачи. До настоящего времени методы, предложенные А.М.Ляпуновым, являются наиболее строгими при исследовании динамики нелинейных систем.

В 1937 году были опубликованы фундаментальные работы А.А.Андронова и С.Э.Хайкина “Теория колебаний”, а также Н.М.Крылова и Н.Н.Боголюбова “Введение в нелинейную механику”. Эти работы, получившие мировую известность, послужили основой для решения важных исследований нелинейных систем.

2.Типовые нелинейные характеристики и особенности процессов в нелинейных САУ

Нелинейности, встречающиеся в системах автоматического управления, могут иметь различный характер. Некоторые нелинейности вводится специально для получения требуемых динамических характеристик регулирования или из-за экономических соображений, т.е. тогда, когда проектируемая с преднамеренно вводимой нелинейностью система имеет выигрыш в весе, стоимости, размерах. При этом предполагается, что рабочие характеристики такой системы должны удовлетворять заданным требованиям.

Другие звенья с нелинейными характеристиками, встречающиеся в системах автоматического управления, нежелательны, и их появление объясняется физическими свойствами отдельных элементов системы. Например, кулоновское трение, прилипание, люфт, насыщение определяют нелинейные участки характеристик звеньев, которые необходимо учитывать при исследовании соответствующих систем.

Нелинейные характеристики в зависимости от вида могут быть разделены на две группы: аналитические и неаналитические. Аналитические характеристики нелинейных звеньев имеют вид плавных однозначных кривых или семейства плавных кривых.

Эти характеристики, как правило, можно описать достаточно простым уравнением. Характеристики неаналитические обычно представляются прерывными или неоднозначными с резкими перегибами.

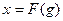
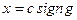
На рис. 22.1 показаны различные формы характеристики реле. Очевидно, такие характеристики невозможно линеаризовать. Идеальная характеристика реле без среднего положения (рис. 22.1,а) может быть представлена так:

,

где символ sign обозначает знак входного сигнала.

Релейные характеристики реле отличаются от рассмотренной выше. Релейная характеристика реле с зоной нечувствительности показана на рис. 22.1,б. Эта характеристика может быть описана следующим образом:

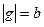
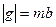
На рис. 22.1,в показана характеристика реле с зоной нечувствительности и петлей гистерезисного типа. Петля характеристики определяется тем, что входной сигнал срабатывания реле больше, чем сигнал отпускания , где m – коэффициент возврата. Аналитическая запись такой характеристики имеет вид:

Рис. 22.1. Релейные характеристики нелинейных элементов

Характеристика реле без среднего положения, имеющая только петлю гистерезисного типа, показана на рис. 22.1,г. Она может быть описана так:

Если реле работает в режиме включения входной цепи одной полярности, то соответствующая характеристика будет иметь несимметричный характер (рис. 22.1, д, е).

Выше рассмотрены были характеристики реле, которые имеют существенно нелинейный характер, однако характеристики и все другие релейных звеньев систем автоматического регулирования в той или иной мере отличаются от идеальной прямой линии. И только для ограниченного интервала изменения входного сигнала некоторые из этих характеристик приближенно можно считать линейными.

На рис. 22.2 показаны нелинейные характеристики некоторых других звеньев систем автоматического регулирования. Характеристика нелинейного элемента (рис. 22.2, а) может быть приближенно описана следующим образом:

где , .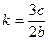

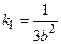
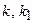
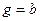
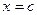
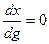
Коэффициенты найдены из условия при , и .

Как видно из рис. 22.2,а, эта характеристика имеет линейную зону и участки насыщения. Под зоной понимается участок характеристики, охватывающий начало координат.

Характеристика элемента с ограничением выходной координаты (рис. 22.2,б) может быть описана так:

Как и предыдущая, характеристика с ограничением выходной координаты имеет зону линейности и участки насыщения.

На рис. 22.2,в показана характеристика звена с зоной нечувствительности и линейными участками. Эта характеристика имеет следующую зависимость выходной координаты от входного сигнала:

Характеристика, изображенная на рис. 22.2,г, по сравнению с предыдущей имеет еще и участки насыщения. Поэтому уравнения для этой характеристики будут иметь вид:

На рис. 22.2,д показана нелинейная характеристика в виде гистерезисной петли. Такая характеристика, имеющая зону неоднозначности, становится особенно сложной, когда ее форма зависит от величины входного сигнала.

Нелинейная характеристика, учитывающая зазор соединений, изображена на рис. 22.2,е. Как и для предыдущего случая, определяющим участком этой характеристики является зона неоднозначности. Соответствующие уравнения имеют вид:

где .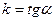

На рис. 22.2,ж показана характеристика нелинейного элемента, имеющего переменный коэффициент усиления.

Рис. 22.2. Характеристики нелинейных элементов

На примере рассмотренных характеристик нелинейных элементов (рис. 22.1, рис. 22.2) можно сделать вывод о том, что наиболее характерными участками этих характеристик являются зоны нечувствительности, зоны и участки линейности, зоны неоднозначности и участки насыщения.

Исследование нелинейных систем является весьма актуальной и важной задачей. Этому вопросу посвящено большое количество работ. Полученные результаты, однако, не являются универсальными и могут быть успешно использованы лишь для решения определенного класса задач.

3. Методы линеаризации нелинейных моделей

При проектировании нелинейных систем автоматического регулирования возникает необходимость в исследовании влияния нелинейных звеньев системы на динамические процессы при всевозможных режимах работы. Для такого рода исследований существует достаточно много различных методов, которые, однако, не могут рассматриваться как универсальные и успешно решают поставленную задачу лишь для определенного типа нелинейности.

Наиболее широкое распространение получили следующие методы анализа нелинейных систем:

— линейной аппроксимации (линеаризации);

Метод линейной аппроксимации. Этот метод применим для анализа таких нелинейных систем, характеристики которых могут быть представлены аналитическими функциями. В этом случае нелинейные функции могут быть разложены в ряд Тейлора. Примерами нелинейных характеристик такого типа являются кривые намагничивания из ферромагнитных материалов. В этом случае, когда нелинейная характеристика имеет резкие перегибы и разрывы, она не может быть описана аналитической функцией. Поэтому исследование таких нелинейностей, как люфт, трение и др., с помощью линейной аппроксимации не представляется возможным.

Если характер нелинейности известен и допускает линеаризацию, приступают к аппроксимации нелинейной характеристики в окрестности предполагаемой рабочей точки. При этом, обычно, используется два способа: метод касательных (разложение в ряд Тейлора) и метод наименьших квадратов. Метод касательных учитывает только первый член ряда Тейлора, поэтому он очень прост и легко может быть применен к характеристикам, заданным как аналитически, так и графически. Метод наименьших квадратов дает лучшую аппроксимацию по критерию минимума среднеквадратической ошибки. Этот метод целесообразно применять в том случае, если рабочая область нелинейной характеристики достаточно велика.

Основное преимущество линейной аппроксимации заключается в том, что в дальнейшем используется линейная методика исследования, что особенно важно при анализе сложных систем автоматического регулирования. Полученные результаты будут справедливы лишь в том случае, если величина входного воздействия нелинейного элемента не выходит за допустимые пределы, поэтому теоретические расчеты должны проверяться экспериментом.

Метод кусочно-линейной аппроксимации. Этот метод предназначен для случая больших вариаций возмущающих воздействий. При этом нелинейные характеристики могут иметь изломы и скачки. Вся характеристика разбивается на прямолинейные участки. Для каждого из этих участков составляются линейные дифференциальные уравнения. Решение этих уравнений производится для определенного диапазона изменения возмущающих сигналов и начальных условий. Рассматриваемый способ может дать очень точные результаты, но для этого потребуется выполнить большой объем вычислительной работы. Объем работы особенно возрастает при исследовании систем высокого порядка и в случае, когда нелинейная характеристика при аппроксимации разбивается на большое число отрезков.

Численные методы. Численные методы интегрирования позволяют решать нелинейные дифференциальные уравнения высокого порядка при больших вариациях возмущающих воздействий относительно рабочей точки. Основной недостаток этих методов заключается в том, что каждый полученный результат характеризует только данную конкретную задачу и не может быть использован при исследовании других нелинейных систем. Каждый из численных методов имеет свои особенности, поэтому задача исследователя заключается в выборе такого численного метода, который наиболее удобен при решении данной конкретной задачи.

Метод фазового пространства (фазовой плоскости). Этот метод является наиболее совершенным аппаратом исследования нелинейных систем, который позволяет получить полную картину возможного поведения системы для различных начальных условий и возмущающих воздействий в виде ступенчатого или линейно-возрастающего сигнала. Метод фазовой плоскости применим для исследования систем с нелинейными элементами с любыми характеристиками. Применяя графическое интегрирование, на основе этого метода можно получить динамические характеристики систем во временной области.

Основной недостаток этого метода заключается в том, что он полностью применим лишь для систем второго порядка. Применение этого метода даже для систем третьего порядка связано с очень большими вычислительными трудностями.

Метод гармонической линеаризации. Этот метод позволяет использовать обычный аппарат частотных характеристик, хорошо известный в линейном анализе. При этом нелинейному элементу приводится в соответствие линейный элемент с эквивалентным комплексным коэффициентом передачи (усиления), который можно рассматривать как своеобразный аналог передаточной функции. Эквивалентный комплексный коэффициент усиления может быть получен в предположении, что входной сигнал нелинейного элемента синусоидален, а выходная координата может быть представлена основной гармоникой ее разложения в ряд Фурье.

Метод гармонической линеаризации достаточно прост и особенно удобен для определения параметров автоколебаний в системе, причем точность этого метода возрастает с увеличением порядка системы. Это объясняется тем, что с увеличением порядка системы возрастают ее фильтрующие свойства, то есть способность подавлять высокочастотные составляющие сигнала. Недостатками этого метода являются малая точность при анализе простых систем, ограничение количества исследуемых нелинейностей и весьма приближенная оценка переходного процесса.

Моделирование. Использование моделирующей установки позволяет исследовать сложные системы со многими нелинейностями при широких вариациях как начальных условий, так и возмущающих воздействий. Такой подход является обязательным на заключительном этапе проектирования, когда объективная оценка системы становится особенно важной. Моделирование нашло применение и при выявлении влияния разброса отдельных параметров на динамические характеристики процесса регулирования.

Дата добавления: 2015-12-11 ; просмотров: 4284 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник