Что такое неопределенность знания об исходе какого либо события

ГДЗ Информатика 10 класс Семакин параграф 4

1. Что такое неопределенность знания об исходе некоторого события?

Неопределенность знания — это количество возможных вариантов ответа на интересовавший вас вопрос. Еще можно сказать: возможных исходов события.

2. Как определяется единица измерения количества информации в рамках содержательного подхода?

В содержательном подходе количество информации, заключенное в сообщении, определяется объемом знаний, который это сообщение несет получающему его человеку. Вспомним, что с «человеческой» точки зрения информация — это знания, которые мы получаем из внешнего мира. Количество информации, заключенное в сообщении, должно быть тем больше, чем больше оно пополняет наши знания. В теории информации для бита дается следующее определение: Сообщение, уменьшающее неопределенность знания в два раза, несет 1 бит информации.

3. Придумайте несколько ситуаций, при которых сообщение несет 1 бит информации.

1. Монета после подбрасывания легла гербом вверх 2. Лампа не горит 3. Телевизор включен 4. Поезд пришел вовремя 5. Можно идти ужинать!

4. В каких случаях и по какой формуле можно вычислить количество информации, содержащейся в сообщении, используя содержательный подход?

5. Сколько битов информации несет сообщение о том, что из колоды в 32 карты достали «даму пик»?

6. При угадывании методом половинного деления целого числа из диапазона от 1 до N был получен 1 байт информации. Чему равно N?

1 байт = 8 бит N = 2^8 = 256

7. Проводятся две лотереи: «4 из 32» и «5 из 64». Сообщение о результатах какой из лотерей несет больше информации?

8. Используя формулу Хартли и электронные таблицы, определите количество информации в сообщениях о равновероятных событиях:

а) на шестигранном игральном кубике выпала цифра 3;

б) в следующем году ремонт в школе начнется в феврале;

в) я приобрел абонемент в бассейн на среду;

г) из 30 учеников класса дежурить в школьной столовой назначили Дениса Скворцова.

Формула Хартли: i = log2N A) Шанс выпадения одной из 6 граней на кубике равен 1/6 i = Iog2 6 = 3 бита Б) В году 12 месяцев, выбор одного уменьшает неопределенность в 12 раз i = Iog2 12 — 4 бита B) В неделе 7 дней, выбор одного дня уменьшает неопределенность в 7 раз i = Iog 27 = 3 бита Г) Выбор одного ученика из 30 снижает неопределенность в 30 раз i = Iog2 30 = 5 бит

9. Используя закон аддитивности количества информации, решите задачу о билете в кинотеатр со следующим дополнительным условием: в кинотеатре 4 зала. В билете указан номер зала, номер ряда и номер места. Какое количество информации заключено в билете?

Источник

«Неопределенность знаний и количество информации»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Кустол Оксана Анатольевна

МБОУ «Раздольненская школа-лицей №1»

Тема: Неопределенность знания и количество информации

образовательная: сформировать представлений об информации, как мере уменьшения неопределенности знания, формировать практические навыки по определению количества информации.

развивающая: развивать умения и навыки решения информационных задач, развить познавательный интерес, информационную культуру, расширять словарный запас по теме « Количество информации как мера уменьшения неопределенности знания »

воспитательная: формировать интерес к предмету, воспитывать настойчивость в преодолении трудностей в учебной работе, воспитать стремление к саморазвитию

Тип урока: изучение нового материала

Форма урока: синтетическая .

Место урока в учебной теме: первичный

Методы и методические приемы:

Материалы и оборудование: презентация, раздаточный материал, проектор, ноутбук

Основные понятия и термины: информация, объем

I. Организационный момент

Приветствие, проверка присутствующих. Объяснение хода урока.

II . Актуализация знаний

сведения, разъяснения, изложение

сведения об окружающем мире и протекающих в нем процессах, воспринимаемые человеком или специальными устройствами

Итак, мы с вами ведем речь об информации и способах измерения информации. Тема нашего урока: «Неопределенность знания и количество информации»

III . Изучение нового материала

Человек всегда стремиться к количественному измерению различных величин. Получая ту или иную информацию, мы понимаем, что не всегда ее бывает достаточно для того, чтобы решить какие-либо проблемы. И как оценить информационный объем книги или статьи?

Содержательный подход позволяет оценить количество информации с точки зрения уменьшения неопределенности наших знаний об объекте.

Рассмотрим, как можно измерить количество информации на примере подбрасывания монеты. Будем считать, то наша монета идеальная: не зависает в воздухе, не падает на ребро и не пропадает момент бросания. Сколько возможных положений может занять монета после подбрасывания?

Ответ учащихся: Два положения: «орел» или «решка».

Неопределенность знания о результате некоторого события — это число возможных результатов события.

Как происходит уменьшение неопределенности знаний

Рассмотрим пример. На книжном стеллаже 8 полок. Сколько информации содержит сообщение о том, где находится книга?

Рассмотрим более сложную задачу. В классе 8 учеников. Учитель хочет узнать, кто дежурный и для этого предлагает детям ответить на предложенные вопросы.

Дежурный сидит на последних двух партах?

Ответ учащихся: Нет.

Дежурный сидит на правом ряду?

Дежурный сидит на первой парте?

Ответ учащихся: Нет

Давайте посмотрим на полученную таблицу. Какова начальная неопределенность?

Какое общее количество информации мы получили?

Ответ учащихся: 3 бита.

Посмотрите на эти числа: 8, 2 и 3. Как они связаны между собой?

Ответ учащихся: 8 равно 2 в кубе.

Следующие соотношения единиц измерения количества информации следует запомнить:

Давайте теперь, используя формулу Хартли, рассчитаем количество информации в различных случаях. Использовать раздаточный материал.

Задача2. В рулетке общее количество лунок равно 128. Какое количество информации мы получим в зрительном сообщении об остановке шарика в одной из лунок.

Задача 3. При угадывании целого числа в диапазоне от 1 до N было получено 9 бит информации. Чему равно N?

Задача4. Загадано слово из 10 букв. Вы просите открыть пятую букву. Вам ее открыли. Сколько информации вы получили?

Эти задачи мы решали коллективно. А теперь я предлагаю вам самостоятельно решить следующую задачу.

В колоде 32 карты. Определите количество информации, содержащейся в сообщениях.

Проверка решения задачи

V . Проверка уровня усвоения материала. Самостоятельная работа.

1. Самостоятельная работа

Источник

Неопределенность знания и количество информации

Содержательный подход к измерению информации отталкивается от определения информации как содержания сообщения, получаемого человеком. Сущность содержательного подхода заключается в следующем: сообщение, информирующее об исходе какого-то события, снимает неопределенность знания человека об этом событии.

Чем больше первоначальная неопределенность знания, тем больше информации несет сообщение, снимающее эту неопределенность.

Приведем примеры, иллюстрирующие данное утверждение.

Ситуация 1. В ваш класс назначен новый учитель информатики; на вопрос «Это мужчина или женщина?» вам ответили: «Мужчина».

Ситуация 2. На чемпионате страны по футболу играли команды «Динамо» и «Зенит». Из спортивных новостей по радио вы узнаете, что игра закончилась победой «Зенита».

Ситуация 3. На выборах мэра города было представлено четыре кандидата. После подведения итогов голосования вы узнали, что избран Н. Н. Никитин.

Вопрос: в какой из трех ситуаций полученное сообщение несет больше информации?

Неопределенность знания — это количество возможных вариантов ответа на интересовавший вас вопрос. Еще можно сказать: возможных исходов события. Здесь событие — например, выборы мэра; исход — выбор, например, Н. Н. Никитина.

В первой ситуации 2 варианта ответа: мужчина, женщина; во второй ситуации 3 варианта: выиграл «Зенит», ничья, выиграло «Динамо»; в третьей ситуации — 4 варианта: 4 кандидата на пост мэра.

Согласно данному выше определению, наибольшее количество информации несет сообщение в третьей ситуации, поскольку неопределенность знания об исходе события в этом случае была наибольшей.

В 40-х годах XX века проблема измерения информации была решена американским ученым Клодом Шенноном — основателем теории информации. Согласно Шеннону, информация — это снятая неопределенность знания человека об исходе какого-то события.

В теории информации единица измерения информации определяется следующим образом.

Сообщение, уменьшающее неопределенность знания об исходе некоторого события в два раза, несет 1 бит информации.

Согласно этому определению, сообщение в первой из описанных ситуаций несет 1 бит информации, поскольку из двух возможных вариантов ответа был выбран один.

Следовательно, количество информации, полученное во второй и в третьей ситуациях, больше, чем один бит. Но как измерить это количество?

Рассмотрим еще один пример.

Ученик написал контрольную по информатике и спрашивает учителя о полученной оценке. Оценка может оказаться любой: от 2 до 5. На что учитель отвечает: «Угадай оценку за два вопроса, ответом на которые может быть только «да» или «нет»». Подумав, ученик задал первый вопрос: «Оценка выше тройки?». «Да», — ответил учитель. Второй вопрос: «Это пятерка?». «Нет», — ответил учитель. Ученик понял, что он получил четверку. Какая бы ни была оценка, таким способом она будет угадана!

Первоначально неопределенность знания (количество возможных оценок) была равна четырем. С ответом на каждый вопрос неопределенность знания уменьшалась в 2 раза и, следовательно, согласно данному выше определению, передавался 1 бит информации.

Узнав оценку (одну из четырех возможных), ученик получил 2 бита информации.

Рассмотрим еще один частный пример, а затем выведем общее правило.

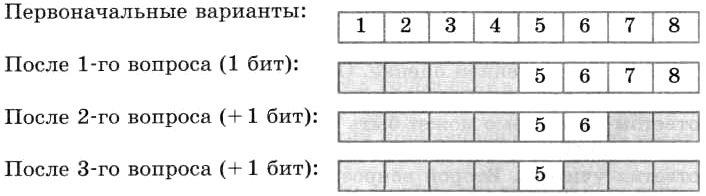
Вы едете на электропоезде, в котором 8 вагонов, а на вокзале вас встречает товарищ. Товарищ позвонил вам по мобильному телефону и спросил, в каком вагоне вы едете. Вы предлагаете угадать номер вагона, задав наименьшее количество вопросов, ответами на которые могут быть только слова «да» или «нет».

Немного подумав, товарищ стал спрашивать:

— Номер вагона больше четырех?— Да.— Номер вагона больше шести?— Нет.— Это шестой вагон?— Нет.— Ну теперь все ясно! Ты едешь в пятом вагоне!

Схематически поиск номера вагона выглядит так:

Каждый ответ уменьшал неопределенность знания в два раза. Всего было задано три вопроса. Значит, в сумме набрано 3 бита информации. То есть сообщение о том, что вы едете в пятом вагоне, несет 3 бита информации.

Способ решения проблемы, примененный в примерах с оценками и вагонами, называется методом половинного деления: ответ на каждый вопрос уменьшает неопределенность знания, имеющуюся перед ответом на этот вопрос, наполовину. Каждый такой ответ несет 1 бит информации.

Заметим, что решение подобных проблем методом половинного деления наиболее рационально. Таким способом всегда можно угадать, например, любой из восьми вариантов за 3 вопроса. Если бы поиск производился последовательным перебором: «Ты едешь в первом вагоне?» «Нет», «Во втором вагоне?» «Нет» и т. д., то про пятый вагон вы смогли бы узнать после пяти вопросов, а про восьмой — после восьми.

«Главная формула» информатики

Сформулируем одно очень важное условие, относящееся к рассмотренным примерам. Во всех ситуациях предполагается, что все возможные исходы события равновероятны. Равновероятно, что учитель может быть мужчиной или женщиной; равновероятен любой исход футбольного матча, равновероятен выбор одного из четырех кандидатов в мэры города. То же относится и к примерам с оценками и вагонами.

Тогда полученные нами результаты описываются следующими формулировками:

• сообщение об одном из двух равновероятных исходов некоторого события несет 1 бит информации;
• сообщение об одном из четырех равновероятных исходов некоторого события несет 2 бита информации;
• сообщение об одном из восьми равновероятных исходов некоторого события несет 3 бита информации.

Обозначим буквой N количество возможных исходов события, или, как мы это еще называли, — неопределенность знания. Буквой i будем обозначать количество информации в сообщении об одном из N результатов.

В примере с учителем: N = 2, i = 1 бит;в примере с оценками: N = 4, i = 2 бита;в примере с вагонами: N = 8, i = 3 бита.

Нетрудно заметить, что связь между этими величинами выражается следующей формулой:

2 i = N.

Действительно: 2 1 = 2 ; 2 2 = 4 ; 2 3 = 8.

С полученной формулой вы уже знакомы из курса информатики для 7 класса и еще не однажды с ней встретитесь. Значение этой формулы столь велико, что мы назвали ее главной формулой информатики. Если величина N известна, a i неизвестно, то данная формула становится уравнением для определения i. В математике такое уравнение называется показательным уравнением.

Пример. Вернемся к рассмотренному выше примеру с вагонами. Пусть в поезде не 8, а 16 вагонов. Чтобы ответить на вопрос, какое количество информации содержится в сообщении о номере искомого вагона, нужно решить уравнение:

2 i = 16.

Количество информации i, содержащееся в сообщении об одном из N равновероятных исходов некоторого события, определяется из решения показательного уравнения:

2 i = N.

Пример. В кинозале 16 рядов, в каждом ряду 32 места. Какое количество информации несет сообщение о том, что вам купили билет на 12-й ряд, 10-е место?

Но эту же задачу можно решать иначе. Сообщение о номере ряда несет 4 бита информации, так как 2 4 = 16. Сообщение о номере места несет 5 битов информации, так как 2 5 = 32. В целом сообщение про ряд и место несет: 4 + 5 = 9 битов информации.

Данный пример иллюстрирует выполнение закона аддитивностиколичества информации (правило сложения): количество информации в сообщении одновременно о нескольких результатах независимых друг от друга событий равно сумме количеств информации о каждом событии отдельно.

Сделаем одно важное замечание. С формулой 2 i = N мы уже встречались, обсуждая алфавитный подход к измерению информации (см. § 3. Измерение информации. Алфавитный подход). В этом случае N рассматривалось как мощность алфавита, а i — как информационный вес каждого символа алфавита. Если допустить, что все символы алфавита появляются в тексте с одинаковой частотой, т. е. равновероятно, то информационный вес символа i тождественен количеству информации в сообщении о появлении любого символа в тексте. При этом N — неопределенность знания о том, какой именно символ алфавита должен стоять в данной позиции текста. Данный факт демонстрирует связь между алфавитным и содержательным подходами к измерению информации.

Формула Хартли

Если значение N равно целой степени двойки (4, 8, 16, 32, 64 и т. д.), то показательное уравнение легко решить в уме, поскольку i будет целым числом. А чему равно количество информации в сообщении о результате матча «Динамо»-«Зенит»? В этой ситуации N = 3. Можно догадаться, что решение уравнения

2 i = 3.

будет дробным числом, лежащим между 1 и 2, поскольку 2 1 = 2 2 = 4 > 3. А как точнее узнать это число?

В математике существует функция, с помощью которой решается показательное уравнение. Эта функция называется логарифмом, и решение нашего уравнения записывается следующим образом:

Читается это так: «логарифм от N по основанию 2». Смысл очень простой: логарифм по основанию 2 от А — это степень, в которую нужно возвести 2, чтобы получить N. Например, вычисление уже известных вам значений можно представить так:

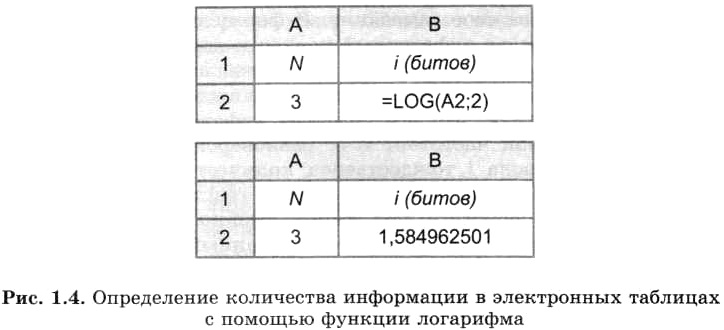
Значения логарифмов находятся с помощью специальных логарифмических таблиц. Также можно использовать инженерный калькулятор или табличный процессор. Определим количество информации, полученной из сообщения об одном исходе события из трех равновероятных, с помощью электронной таблицы. На рисунке 1.4 представлены два режима электронной таблицы: режим отображения формул и режим отображения значений.

В табличном процессоре Microsoft Excel функция логарифма имеет следующий вид: LOG(apryмент; основание). Аргумент — значение N находится в ячейке А2, а основание логарифма равно 2. В результате получаем с точностью до девяти знаков после запятой: i = log₂3 = 1,584962501 (бита).

Формула для измерения количества информации: i = log₂N была предложена американским ученым Ральфом Хартли — одним из основоположников теории информации.

Формула Хартли: i = log₂ N
Здесь i — количество информации, содержащееся в сообщении об одном из N равновероятных исходов события.

Данный пример показал, что количество информации, определяемое с использованием содержательного подхода, может быть дробной величиной, в то время как информационный объем, вычисляемый путем применения алфавитного подхода, может иметь только целочисленное значение.

Источник

Что такое неопределенность знания об исходе некоторого события?

Обсуждение вопроса:

Неопределенность знаний о некотором событии – это количество возможных результатов события (бросания монеты, кубика; вытаскивание жребия).

Это количество возможных исходов в данном событии.

Неопределенность знаний об исходе некоторого события равна количеству возможных исходов в этом событии. Но сама неопределенность не есть количество.

Неопределенность — это состояние, обратное определенности.

Информация — это снятая неопределенность. Величина неопределенности некоторого события — это количество возможных результатов (исходов) данного события.

Допустим, вы подбрасываете монету, загадывая, что выпадет: «орел» или «решка». Перед подбрасыванием монеты неопределенность знания о результате равна двум. Действительно, есть всего два возможных результата этого события (бросания монеты). Эти результаты мы считаем равновероятными, т. к. ни один из них не имеет преимущества перед другим.

В ваш класс назначен новый учитель информатики; на вопрос: «Это мужчина или женщина», вам ответили: «Мужчина». (2 варианта)

На чемпионате страны по футболу играли команды Динамо и Зенит. Из спортивных новостей по радио вы узнаете, что игра закончилась победой Зенита. (3 варианта)

На выборах мера города было четыре кандидата. После подведения итогов голосования вы узнали, что избран Никитин Н.Н. (4 варианта)

Источник

Неопределенность знания о результате какого либо события. Понятие энтропии

Чем больше первоначальная неопределенность знания, тем больше информации несет сообщение, снимающее эту неопределенность.

Приведем примеры, иллюстрирующие данное утверждение.

Ситуация 1. В ваш класс назначен новый учитель информатики; на вопрос «Это мужчина или женщина?» вам ответили: «Мужчина».

Ситуация 2. На чемпионате страны по футболу играли команды «Динамо» и «Зенит». Из спортивных новостей по радио вы узнаете, что игра закончилась победой «Зенита».

Ситуация 3. На выборах мэра города было представлено четыре кандидата. После подведения итогов голосования вы узнали, что избран Н. Н. Никитин.

Вопрос: в какой из трех ситуаций полученное сообщение несет больше информации?

Согласно данному выше определению, наибольшее количество информации несет сообщение в третьей ситуации, поскольку неопределенность знания об исходе события в этом случае была наибольшей.

В теории информации единица измерения информации определяется следующим образом.

Согласно этому определению, сообщение в первой из описанных ситуаций несет 1 бит информации, поскольку из двух возможных вариантов ответа был выбран один.

Следовательно, количество информации, полученное во второй и в третьей ситуациях, больше, чем один бит. Но как измерить это количество?

Рассмотрим еще один пример.

Первоначально неопределенность знания (количество возможных оценок) была равна четырем. С ответом на каждый вопрос неопределенность знания уменьшалась в 2 раза и, следовательно, согласно данному выше определению, передавался 1 бит информации.

Узнав оценку (одну из четырех возможных), ученик получил 2 бита информации.

Рассмотрим еще один частный пример, а затем выведем общее правило.

Вы едете на электропоезде, в котором 8 вагонов, а на вокзале вас встречает товарищ. Товарищ позвонил вам по мобильному телефону и спросил, в каком вагоне вы едете. Вы предлагаете угадать номер вагона, задав наименьшее количество вопросов, ответами на которые могут быть только слова «да» или «нет».

Немного подумав, товарищ стал спрашивать:

Номер вагона больше четырех?

Номер вагона больше шести?

Ну теперь все ясно! Ты едешь в пятом вагоне!

Схематически поиск номера вагона выглядит так:

Каждый ответ уменьшал неопределенность знания в два раза. Всего было задано три вопроса. Значит, в сумме набрано 3 бита информации. То есть сообщение о том, что вы едете в пятом вагоне, несет 3 бита информации.

Способ решения проблемы, примененный в примерах с оценками и вагонами, называется методом половинного деления: ответ на каждый вопрос уменьшает неопределенность знания, имеющуюся перед ответом на этот вопрос, наполовину. Каждый такой ответ несет 1 бит информации.

«Главная формула» информатики

Сформулируем одно очень важное условие, относящееся к рассмотренным примерам. Во всех ситуациях предполагается, что все возможные исходы события равновероятны. Равновероятно, что учитель может быть мужчиной или женщиной; равновероятен любой исход футбольного матча, равновероятен выбор одного из четырех кандидатов в мэры города. То же относится и к примерам с оценками и вагонами.

Тогда полученные нами результаты описываются следующими формулировками:

В примере с учителем: N = 2, i = 1 бит;

в примере с оценками: N = 4, i = 2 бита;

в примере с вагонами: N = 8, i = 3 бита.

Нетрудно заметить, что связь между этими величинами выражается следующей формулой:

2 i = N. Действительно: 2 1 = 2 ; 2 2 = 4 ; 2 3 = 8.

С полученной формулой вы уже знакомы из курса информатики для 7 класса и еще не однажды с ней встретитесь. Значение этой формулы столь велико, что мы назвали ее главной формулой информатики. Если величина N известна, a i неизвестно, то данная формула становится уравнением для определения i. В математике такое уравнение называется показательным уравнением.

Пример. Вернемся к рассмотренному выше примеру с вагонами. Пусть в поезде не 8, а 16 вагонов. Чтобы ответить на вопрос, какое количество информации содержится в сообщении о номере искомого вагона, нужно решить уравнение:

Пример. В кинозале 16 рядов, в каждом ряду 32 места. Какое количество информации несет сообщение о том, что вам купили билет на 12-й ряд, 10-е место?

Решение задачи: в кинозале всего 16 32 = 512 мест. Сообщение о купленном билете однозначно определяет выбор одного из этих мест. Из уравнения 2 i = 512 = 29 получаем: i = 9 битов.

Но эту же задачу можно решать иначе. Сообщение о номере ряда несет 4 бита информации, так как 2 4 = 16. Сообщение о номере места несет 5 битов информации, так как 2 5 = 32. В целом сообщение про ряд и место несет: 4 + 5 = 9 битов информации.

Данный пример иллюстрирует выполнение закона аддитивности количества информации (правило сложения): количество информации в сообщении одновременно о нескольких результатах независимых друг от друга событий равно сумме количеств информации о каждом событии отдельно.

Формула Хартли

Если значение N равно целой степени двойки (4, 8, 16, 32, 64 и т. д.), то показательное уравнение легко решить в уме, поскольку i будет целым числом. А чему равно количество информации в сообщении о результате матча «Динамо»-«Зенит»? В этой ситуации N = 3. Можно догадаться, что решение уравнения

будет дробным числом, лежащим между 1 и 2, поскольку 2 1 = 2 3. А как точнее узнать это число?

В математике существует функция, с помощью которой решается показательное уравнение. Эта функция называется логарифмом, и решение нашего уравнения записывается следующим образом:

log 2 2 = 1, log 2 4 = 2, log 2 8 = 3.

Значения логарифмов находятся с помощью специальных логарифмических таблиц. Также можно использовать инженерный калькулятор или табличный процессор. Определим количество информации, полученной из сообщения об одном исходе события из трех равновероятных, с помощью электронной таблицы. На рисунке 1.4 представлены два режима электронной таблицы: режим отображения формул и режим отображения значений.

Рис. 1.4. Определение количества информации в электронных таблицах с помощью функции логарифма

Данный пример показал, что количество информации, определяемое с использованием содержательного подхода, может быть дробной величиной, в то время как информационный объем, вычисляемый путем применения алфавитного подхода, может иметь только целочисленное значение.

Система основных понятий

Вопросы и задания

а) на шестигранном игральном кубике выпала цифра 3;

б) в следующем году ремонт в школе начнется в феврале;

в) я приобрел абонемент в бассейн на среду;

г) из 30 учеников класса дежурить в школьной столовой назначили Дениса Скворцова.

Энтропия (H ) – мера неопределенности, выраженная в битах. Так же энтропию можно рассматривать как меру равномерности распределения случайной величины.

Максимального значения энтропия достигает в данном случае тогда, когда обе вероятности равны между собой и равны ½, нулевое значение энтропии соответствует случаям (p 0 =0, p 1 =1) и (p 0 =1, p 1 =0).

Случайные события могут быть описаны с использованием понятия «вероятность». Соотношения теории вероятностей позволяют найти (вычислить) вероятности как одиночных случайных событий, так и сложных опытов, объединяющих несколько независимых или связанных между собой событий. Однако описать случайные события можно не только в терминах вероятностей.

То, что событие случайно, означает отсутствие полной уверенности в его наступлении, что, в свою очередь, создает неопределенность в исходах опытов, связанных с данным событием. Безусловно, степень неопределенности различна для разных ситуаций.

Например, если опыт состоит в определении возраста случайно выбранного студента 1-го курса дневного отделения вуза, то с большой долей уверенности можно утверждать, что он окажется менее 30 лет; хотя по положению на дневном отделении могут обучаться лица в возрасте до 35 лет, чаще всего очно учатся выпускники школ ближайших нескольких выпусков. Гораздо меньшую определенность имеет аналогичный опыт, если проверяется, будет ли возраст произвольно выбранного студента меньше 18 лет. Для практики важно иметь возможность произвести численную оценку неопределенности разных опытов. Попробуем ввести такую количественную меру неопределенности.

Начнем с простой ситуации, когда опыт имеет %%n%% равновероятных исходов. Очевидно, что неопределенность каждого из них зависит от n, т.е.

Мера неопределенности является функцией числа исходов %%f(n)%%.

Можно указать некоторые свойства этой функции:

$$f(n_α \cdot n_β)=f(n_α)+f(n_β)

Теперь задумаемся о том, каким может быть явный вид функции %%f(n)%%, чтобы он удовлетворял свойствам (1) и (2) и соотношению (2.1)? Легко увидеть, что такому набору свойств удовлетворяет функция %%log(n)%%, причем можно доказать, что она единственная из всех существующих классов функций. Таким образом:

За меру неопределенности опыта с n равновероятными исходами можно принять число %%log(n)%%.

Следует заметить, что выбор основания логарифма в данном случае значения не имеет, поскольку в силу известной формулы преобразования логарифма от одного основания к другому.

переход к другому основанию состоит во введении одинакового для обеих частей выражения (2.1) постоянного множителя %%log_b а%%, что равносильно изменению масштаба (т.е. размера единицы) измерения неопределенности. Поскольку это так, имеется возможность выбрать удобное (из каких-то дополнительных соображений) основание логарифма. Таким удобным основанием оказывается 2, поскольку в этом случае за единицу измерения принимается неопределенность, содержащаяся в опыте, имеющем лишь два равновероятных исхода, которые можно обозначить, например, ИСТИНА (True) и ЛОЖЬ (False) и использовать для анализа таких событий аппарат математической логики.

Название бит происходит от английского binary digit, что в дословном переводе означает «двоичный разряд» или «двоичная единица».

Таким образом, нами установлен явный вид функции, описывающей меру неопределенности опыта, имеющего %%n%% равновероятных исходов:

Вновь рассмотрим опыт с %%n%% равновероятными исходами. Поскольку каждый исход случаен, он вносит свой вклад в неопределенность всего опыта, но так как все %%n%% исходов равнозначны, разумно допустить, что и их неопределенности одинаковы. Из свойства аддитивности неопределенности, а также того, что согласно (2.2) общая неопределенность равна %%log_2 n%%, следует, что неопределенность, вносимая одним исходом составляет

Таким образом, неопределенность, вносимая каждым из равновероятных исходов, равна:

Теперь попробуем обобщить формулу (2.3) на ситуацию, когда исходы опытов неравновероятны, например, %%p(A_1)%% и %%p(A_2)%%. Тогда:

$$H=H_1+H_2=-p(А_1) \cdot log_2 р(А_1)-p(А_2) \cdot log_2 р(А_2)$$

Обобщая это выражение на ситуацию, когда опыт %%α%% имеет %%n%% неравновероятных исходов %%А_1, А_2. А_n%%, получим:

Введенная таким образом величина, как уже было сказано, называется энтропией опыта. Используя формулу для среднего значения дискретных случайных величин, можно записать:

Энтропия является мерой неопределенности опыта, в котором проявляются случайные события, и равна средней неопределенности всех возможных его исходов.

Для практики формула (2.4) важна тем, что позволяет сравнить неопределенности различных опытов со случайными исходами.

Согласно (2.4) находим энтропии обоих опытов:

%%Н_β > Н_α%%, т.е. неопределенность результата в опыте β выше и, следовательно, предсказать его можно с меньшей долей уверенности, чем результат α.

КОЛИЧЕСТВЕННАЯ МЕРА НЕОПРЕДЕЛЁННОСТИ

Для сравнения неопределённостей, рассмотрим следующие примеры или опыты a, b и g, содержащие неопределённости H(a), H(b) и H(g) соответственно:

1. Определить очередного чемпиона мира по шахматам (опыт a).

2. Определить номер лотерейного билета, на который выпадет наибольший выигрыш в предстоящем тираже лотереи (опыт b).

3. Определить следующего президента РФ (опыт g).

Очевидно, степень неопределённости каждого опыта отличается от двух других, причём скорее всего имеют место неравенства

При k= 1 H(a) = 0, а при возрастании k H(a) также возрастает, т.е.

Таким образом, в качестве функции f можно выбрать логарифмическую функцию и считать, что

Это есть формула Хартли и она представляет собой меру неопределённости относительно опыта a, содержащимся в опыте a и имеющим два равновероятных исхода (например,»да» или «нет»). Другими словами, H(a) это то количество информации (за единицей измерения количества информации считается бит), с помощью которого неопределённость опыта a превращается в достоверность.

Так, например, для угадывания задуманного числа в диапазоне от 1 до 8 необходимо максимум 3 бит информации, т.е. необходимо задать три вопроса.

3.1.1. Доказать, что H(ab) = H(a) + H(b).

3.1.2. Сколько вопросов необходимо задать студентам академической группы преподавателю, чтобы определить старосту этой группы (ответы на вопросы преподавателя могут быть либо «да» либо «нет»).

3.1.3. Рассмотреть задачу 3.1.2. в случае одного вопроса.

3.1.4. Пусть х- элемент множества М мощности m. Какое количество

информации необходимо для определения элемента х?

3.1.6. Пусть имеется 27 золотых монет, из которых одна фальшивая (легче настоящих), и весы с чашками. Сколько взвешиваний необходимо произвести, чтобы определить фальшивую монету?

3.1.7. Доказать, что любого опыта a H(a) ³ 0, причём H(a) = 0 тогда и только тогда, когда одна из вероятностей равна 1, а остальные равны 0.

а если же a и b зависимы, то

Имеет место также равенство

что можно трактовать примерно так: от всего, чему учат в университете, вреда не будет, а в худшем случае просто не будет пользы.

3.2.1. Доказать, что если a и b произвольные опыты, то;

3.2.5. (О городах лжецов и честных людей). Пусть известно, что жители некоторого города А всегда говорят правду, а жители соседнего города Б всегда обманывают. Наблюдатель Н знает, что он находится в одном из этих двух городов, но не знает, в каком именно. Путём опроса встречного ему требуется определить, в каком городе он находится, или в каком городе живёт его собеседник (жители А могут заходить в Б и обратно), или то и другое вместе. Спрашивается, каково наименьшее число вопросов, которые должен задать Н (на все вопросы Н встречный отвечает лишь «да» или «нет»).

Ещё раз вернёмся к общей схеме передачи информации, рассматривая реальные сообщения как некоторые опыты с соответствующими таблицами распределения вероятностей в них отдельных букв или сочетания букв.

где Н(х), Н(х») энтропии сообщений х и х» соответственно.

называется пропускной способностью канала, т.е. она характеризует максимальное количество информации, которое может быть передано через канал за один такт времени. А в самом деле, пропускная способность канала является верхней границей скорости R надёжной передачи информации, причём к этой границе можно подойти сколь угодно близко.

В то же время всякий способ передачи информации со скоростью, большей пропускной способности, приводит к тому, что вероятность ошибки будет больше некоторой фиксированной величины.

Теорема 2. (обращение теоремы кодирования). Если величина R превосходит пропускную способность канала С, то найдётся константа e 0 (зависящая от R и C) такая, что при любом способе блоковой передачи информации со скоростью, не меньшей R, выполнено неравенство

Обозначим через I(a i) количество информации, содержащееся в символе a i и определим его как:

Если же текст сообщений записан на некотором естественном языке

а избыточность С L соответственно как

Очевидно, что 0 ≤ С L ≤ 1, следовательно, при оптимальном кодировании часть текста можно без ущерба для понимания опустить.

Так, например, С L = 0.5 для литературного английского языка, а избыточность других языков несколько меньше.

3.3.1. Определить пропускную способность ДСК.

3.3.3. Определить избыточность и неопределённость русского языка.

3.3.4. Определить количество информации букв английского языка.

3.3.5. Доказать теоремы Шеннона для блочных кодов.

3.3.6. Восстановить текст:

Осипян Валерий Осипович

ЭЛЕМЕНТЫ ТЕОРИИ ПЕРЕДАЧИ ИНФОРМАЦИИ

Технический редактор И.А. Зиновская

Корректор М.Е. Шулепова

ЛР № 200378 от 22.01.97

Подписано в печать 29.01.97.

Формат 60´84 1 /16. Бумага тип. № 3.

Печать трафаретная. Усл. печ. л. 2,75.

Уч.-изд. л. 2,7. Тираж 300 экз. Заказ №

Кубанский государственный университет

Случайность и неопределенность

Комбинаторика — это раздел математики, изучаю­щий сочетания, перестановки, размещения и перечис­ления элементов множества.

Что такое неопределенность?

Неопределенность — это недостаток или отсутст­вие информации о чем-либо.

Случайность — это категория для обозначения свя­зей между такими явлениями реального мира, кото­рые в одних условиях могут осуществиться, а в дру­гих — нет. Случайность события заключается в том, что реализация того или иного исхода имеет некото­рую степень неопределенности.

Случайность проявляется практически во всех об­ластях деятельности человека.

Событие — это явление, произошедшее в результа­те действий. События обычно обозначаются большими латинскими буквами: А, В, С и т. д.

Случайное событие — это событие, которое может как произойти, так и не произойти.

Суммой событий Ай В называется событие С, кото­рое состоит в появлении события А или события В или обоих событий сразу:

Произведением событий А и В называется событие С, которое состоит в совместном появлении событий А и В (их совмещении):

Вероятность события — это мера объективной воз­можности появления события.

Событие А называется независимым от события В, если вероятность события А не зависит от того, насту­пило событие В или нет. Иначе событие А называется зависимым от события В.

Несовместными называются события, которые не могут наступить одновременно: наступление одного исключает появление другого.

Алгоритмы генерации псевдослучайных последовательностей периодичны.

Примеры. 1. Определить вероятность появления грани игрального кубика с числом 6.

В этом случае количество общих исходов равно 6, поскольку в игральном кубике 6 граней. Однако благоприятный исход только один, так как у кубика только одна грань с цифрой 6, поэтому

Пример 2. Сгенерировать список чисел от 1 до N, рас­положенный в случайном порядке.

Если позиция элемента содержит «О», можно помещать элемент.

Если позиция не «О», то генерируется случайный номер для элемента.

Присваиваем элементам списка нулевые значения.

Помещаем элемент в последовательность.

Если позиция не «0», то проверяем все последующие, пока не найдём «0».

Присваиваем элементам списка нулевые значения.

Помещаем элемент в последовательность.

Если позиция элемента содержит «0», можно помещать элемент.

Источник