Что такое непересекающиеся множества
Система непересекающихся множеств и её применения
Добрый день, Хабрахабр. Это еще один пост в рамках моей программы по обогащению базы данных крупнейшего IT-ресурса информацией по алгоритмам и структурам данных. Как показывает практика, этой информации многим не хватает, а необходимость встречается в самых разнообразных сферах программистской жизни.
Я продолжаю преимущественно выбирать те алгоритмы/структуры, которые легко понимаются и для которых не требуется много кода — а вот практическое значение сложно недооценить. В прошлый раз это было декартово дерево. В этот раз — система непересекающихся множеств. Она же известна под названиями disjoint set union (DSU) или Union-Find.
Условие
Поставим перед собой следующую задачу. Пускай мы оперируем элементами N видов (для простоты, здесь и далее — числами от 0 до N-1). Некоторые группы чисел объединены в множества. Также мы можем добавить в структуру новый элемент, он тем самым образует множество размера 1 из самого себя. И наконец, периодически некоторые два множества нам потребуется сливать в одно.
Формализируем задачу: создать быструю структуру, которая поддерживает следующие операции:
На рисунке я продемонстрирую работу такой гипотетической структуры.
Реализация
Классическая реализация DSU была предложена Bernard Galler и Michael Fischer в 1964 году, однако исследована (включая временную оценку сложности) Робертом Тарьяном уже в 1975. Тарьяну же принадлежат некоторые результаты, улучшения и применения, о которых мы сегодня ещё поговорим.
Хранить структуру данных будем в виде леса, то есть превратим DSU в систему непересекающихся деревьев. Все элементы одного множества лежат в одном соответствующем дереве, представитель дерева — его корень, слияние множеств суть просто объединение двух деревьев в одно. Как мы увидим, такая идея вкупе с двумя небольшими эвристиками ведет к поразительно высокому быстродействию получившейся структуры.
Для начала нам потребуется массив p, хранящий для каждой вершины дерева её непосредственного предка (а для корня дерева X — его самого). С помощью одного только этого массива можно эффективно реализовать две первые операции DSU:
MakeSet(X)
Чтобы создать новое дерево из элемента X, достаточно указать, что он является корнем собственного дерева, и предка не имеет.
Find(X)
Представителем дерева будем считать его корень. Тогда для нахождения этого представителя достаточно подняться вверх по родительским ссылкам до тех пор, пока не наткнемся на корень.
Но это еще не все: такая наивная реализация в случае вырожденного (вытянутого в линию) дерева может работать за O(N), что недопустимо. Можно было бы попытаться ускорить поиск. Например, хранить не только непосредственного предка, а большие таблицы логарифмического подъема вверх, но это требует много памяти. Или хранить вместо ссылки на предка ссылку на собственно корень — однако тогда при слиянии деревьев (Unite) придется менять эти ссылки всем элементам одного из деревьев, а это опять-таки временные затраты порядка O(N).
Мы пойдем другим путём: вместо ускорения реализации будем просто пытаться не допускать чрезмерно длинных веток в дереве. Это первая эвристика DSU, она называется сжатие путей (path compression). Суть эвристики: после того, как представитель таки будет найден, мы для каждой вершины по пути от X к корню изменим предка на этого самого представителя. То есть фактически переподвесим все эти вершины вместо длинной ветви непосредственно к корню. Таким образом, реализация операции Find становится двухпроходной.
На рисунке показано дерево до и после выполнения операции Find(3). Красные ребра — те, по которым мы прошлись по пути к корню. Теперь они перенаправлены. Заметьте, как после этого кардинально уменьшилась высота дерева.
Исходный код в рекурсивной форме написать достаточно просто:
Unite(X, Y)
Со слиянием двух деревьев придется чуть повозиться. Найдем для начала корни обоих сливаемых деревьев с помощью уже написанной функции Find. Теперь, помня, что наша реализация хранит только ссылки на непосредственных родителей, для слияния деревьев достаточно было бы просто подвесить один из корней (а с ним и все дерево) сыном к другому. Таким образом все элементы этого дерева автоматически станут принадлежать другому — и процедура поиска представителя будет возвращать корень нового дерева.
Встает вопрос: какое дерево к какому подвешивать? Всегда выбирать какое-то одно, скажем, дерево X, не годится: легко подобрать пример, на котором после N объединений мы получим вырожденное дерево — одну ветку из N элементов. И тут в ход вступает вторая эвристика DSU, направленная на уменьшение высоты деревьев.
Будем хранить помимо предков еще один массив Rank. В нем для каждого дерева будет храниться верхняя граница его высоты — то есть длиннейшей ветви в нем. Заметьте, не сама высота — в процессе выполнения Find длиннейшая ветвь может самоуничтожиться, а тратить еще итерации на нахождение новой длиннейшей ветви слишком дорого. Поэтому для каждого корня в массиве Rank будет записано число, гарантированно больше или равное высоте его дерева.
Теперь легко принять решении о слиянии: чтобы не допустить слишком длинных ветвей в DSU, будем подвешивать более низкое дерево к более высокому. Если их высоты равны — не играет роли, кого подвешивать к кому. Но в последнем случае новоиспеченному корню надо не забыть увеличить Rank.
Вот так производится типичный Unite (например, с параметрами 8 и 19):
Однако на практике оказывается, что можно и не тратить дополнительные O(N) памяти на махинации с рангами. Достаточно выбирать корень для переподвешивания случайным образом — как ни удивительно, но такое решение дает на практике скорость, вполне сравнимую с оригинальной ранговой реализацией. Автор данной статьи всю жизнь пользуется именно рандомизированным DSU, и еще не было случая, когда тот бы подвёл.
Быстродействие
В силу применения двух эвристик скорость работы каждой операции сильно зависит от структуры дерева, а структура дерева — от списка выполненных до того операций. Исключение составляет только MakeSet — её время работы очевидно O(1) 🙂 Для остальных двух скорость очень неочевидна.
Итак, имеем:
MakeSet(X) — O(1).
Find(X) — O(1) амортизированно.
Unite(X, Y) — O(1) амортизированно.
Расход памяти — O(N).
Практические применения
Для DSU известно большое число различных использований. Большинство связано с решением некоторой задачи в режиме оффлайн — то есть когда список запросов касательно структуры, которые поступают программе, известен заранее. Я приведу здесь несколько таких задач вместе с краткими идеями решений.
Остов минимального веса
Дан неориентированный связный граф со взвешенными ребрами. Выкинуть из него некоторые ребра так, чтобы в итоге получилось дерево, причем суммарный вес ребер этого дерева должен быть наименьшим.
Одно из известных мест, где встает эта задача (хотя и решается иначе) — блокирование избыточных связей в Ethernet-сети для избегания возможных циклов пакетов. Протоколы, созданные с этой целью, широко известны, причем половина серьезных модификаций в них сделана Cisco. Более подробно см. Spanning Tree Protocol.
На рисунке показан взвешенный граф с выделенным минимальным остовом.
Алгоритм Краскала для решения этой задачи: отсортируем все ребра по возрастанию веса и будем поддерживать текущий лес минимального веса с помощью DSU. Изначально DSU состоит из N деревьев, по одной вершине в каждом. Идем по ребрам в порядке возврастания; если текущее ребро объединяет разные компоненты — сливаем их в одну и запоминаем ребро как элемент остова. Как только количество компонент достигнет единицы — мы построили искомое дерево.
Алгоритм Тарьяна для поиска LCA оффлайн
Дано дерево и набор запросов вида: для данных вершин u и v вернуть их ближайшего общего предка (least common ancestor, LCA). Весь набор запросов известен заранее, т.е. задача сформулирована в режиме оффлайн.
Компоненты связности в мультиграфе
Дан мультиграф (граф, в котором пара вершин может быть соединена более чем одним непосредственным ребром), к которому поступают запросы вида «удалить некоторое ребро» и «а сколько сейчас в графе компонент связности?» Весь список запросов известен заранее.
Решение банально. Выполним сначала все запросы на удаление, посчитаем количество компонент в итоговом графе, запомним его. Получившийся граф запихнем в DSU. Теперь будем идти по запросам удаления в обратном порядке: каждое удаление ребра из старого графа означает возможное слияние двух компонент в нашем «flashback-графе», хранящемся в DSU; в таком случае текущее количество компонент связности уменьшается на единичку.
Сегментирование изображений
Рассмотрим некоторое изображение — прямоугольный массив пикселей. Его можно представить как сетчатый граф: каждая вершина-пиксель непосредственно связана ребрами со своими четырьмя ближайшими соседями. Задача заключается в том, чтобы выделить на изображении одинаковые смысловые зоны, например, похожего цвета, и уметь для двух пикселей быстро определять, находятся ли они в одной зоне. Так, например, раскрашиваются старые черно-белые фильмы: для начала нужно выделить области с примерно одинаковыми оттенками серого.
Есть два подхода к решению этой проблемы, оба в конечном итоге используют DSU. В первом варианте мы проводим ребро не между каждой парой соседних пикселей, а только между теми, которые достаточно близки по цвету. После этого обычный прямоугольный обход графа заполнит DSU, и мы получим набор компонент связности — они же однотонные области изображения.
Второй вариант более гибкий. Не будем полностью убирать ребра, а присвоим каждому из них вес, рассчитанный на основании разности цветов и еще каких-то дополнительных факторов — своих для каждой конкретной задачи сегментирования. В полученном графе достаточно найти какой-нибудь лес минимального веса, например, тем же алгоритмом Краскала. На практике в DSU записывают не любое текущее соединяющее ребро, а только те, для которых на данный момент две компоненты не сильно отличаются по меркам другой специальной весовой функции.
Генерация лабиринтов
Задача: сгенерировать лабиринт с одним входом и одним выходом.
Алгоритм решения:
Начнем с состояния, когда установлены все стены, за исключением входа и выхода.
На каждом шаге алгоритма выберем случайную стену. Если ячейки, между которыми она стоит, еще никак не соединены (лежат в разных компонентах DSU), то уничтожаем её (сливаем компоненты).
Продолжаем процесс до некоторого состояния сходимости: например, когда вход и выход соединены; либо, когда осталась одна компонента.
Однопроходные алгоритмы
Существуют варианты реализации Find(X), которые требуют одного прохода до корня, а не двух, однако сохраняют ту же или почти ту же степень быстродействия. Они реализуют другие стратегии сокращения высоты дерева, в отличие от path compression.
Вариант №1: path splitting. По пути от вершины Х до корня перенаправить родительскую связь каждой вершины с её предка на предка предка (дедушку).
Вариант №2: path halving. Взять идею path splitting, однако перенаправлять связи не всех вершин по пути, а только тех, на которых делаем перенаправления — то есть «дедушек».
На рисунке взято все то же дерево, в нем выполняется запрос Find(3). По центру показан результат с применением path splitting, справа — path halving.
Функциональная реализация
У системы непересекающихся множеств есть один большой недостаток: она не поддерживает ни в какой форме операцию Undo, потому что реализована насквозь в императивном стиле. Гораздо удобнее была бы реализация DSU в функциональном стиле, когда каждая операция не изменяет структуру на месте, а возвращает слегка модифицированную новую структуру, в которой произведены требуемые изменения (при этом большая часть памяти у старой и новой структур общая). Такие структуры данных в английской терминологии носят название persistent, они широко применяются в чистом функциональном программировании, где доминирует идея неизменяемости данных.
В силу чисто императивной идеи алгоритмов DSU её функциональная реализация с сохранением быстродействия долгое время казалась немыслимой. Тем не менее, в 2007 году Sylvain Conchon и Jean-Christophe Filliâtre представили в своей работе искомый функциональный вариант, в котором операция Unite возвращает измененную структуру. Если говорить честно, он не совсем функциональный, он использует императивные присваивания, однако они надежно скрыты внутри реализации, а интерфейс persistent DSU — чисто функциональный.
Основная идея реализации — использование структур данных, реализующих «персистентные массивы»: они поддерживают те же операции, что и массивы, однако все так же не модифицируют память, а возвращают измененную структуру. Такой массив можно легко реализовать с помощью какого-нибудь дерева, однако в таком случае операции с ним будут занимать O(log2 N) времени, а для DSU такая оценка оказывается уже чрезмерно большой.
За дальнейшими техническими подробностями отсылаю читателей к оригинальной статье.
Литература
Системы непересекающихся множеств в объеме данной статьи обсуждаются в знаменитой книге — Кормен, Лейзерсон, Ривест, Штайн «Алгоритмы: построение и анализ». Там же можно найти и доказательство того, что выполнение операций занимает порядка α(N) времени.
На сайте Максима Иванова можно найти полную реализацию DSU на C++.
В статье Wait-free Parallel Algorithms for the Union-Find Problem обсуждается парралельная версия реализации DSU. В ней отсутствуют блокировки потоков.
Система непересекающихся множеств
В данной статье рассматривается структура данных «система непересекающихся множеств» (на английском «disjoint-set-union», или просто «DSU»).
Эта структура данных предоставляет следующие возможности. Изначально имеется несколько элементов, каждый из которых находится в отдельном (своём собственном) множестве. За одну операцию можно объединить два каких-либо множества, а также можно запросить, в каком множестве сейчас находится указанный элемент. Также, в классическом варианте, вводится ещё одна операция — создание нового элемента, который помещается в отдельное множество.
Таким образом, базовый интерфейс данной структуры данных состоит всего из трёх операций:
Например, если вызов 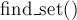
Описываемая ниже структура данных позволяет делать каждую из этих операций почти за 
Также в одном из подразделов статьи описан альтернативный вариант реализации DSU, позволяющий добиться асимптотики 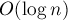



Построение эффективной структуры данных
Определимся сначала, в каком виде мы будем хранить всю информацию.
Множества элементов мы будем хранить в виде деревьев: одно дерево соответствует одному множеству. Корень дерева — это представитель (лидер) множества.
При реализации это означает, что мы заводим массив 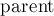
Наивная реализация
Мы уже можем написать первую реализацию системы непересекающихся множеств. Она будет довольно неэффективной, но затем мы улучшим её с помощью двух приёмов, получив в итоге почти константное время работы.
Итак, вся информация о множествах элементов хранится у нас с помощью массива 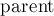
Чтобы создать новый элемент (операция 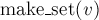

Чтобы объединить два множества (операция 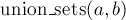




Наконец, реализация операции поиска лидера (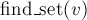

Впрочем, такая реализация системы непересекающихся множеств весьма неэффективна. Легко построить пример, когда после нескольких объединений множеств получится ситуация, что множество — это дерево, выродившееся в длинную цепочку. В результате каждый вызов 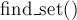

Это весьма далеко от той асимптотики, которую мы собирались получить (константное время работы). Поэтому рассмотрим две оптимизации, которые позволят (даже применённые по отдельности) значительно ускорить работу.
Эвристика сжатия пути
Эта эвристика предназначена для ускорения работы 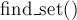
Она заключается в том, что когда после вызова 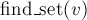



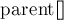

Таким образом, у массива предков 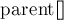
С другой стороны, понятно, что нельзя сделать, чтобы эти указатели 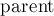
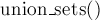

Таким образом, к массиву 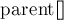
Новая реализация операции 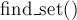
Такая простая реализация делает всё, что задумывалось: сначала путём рекурсивных вызовов находится лидера множества, а затем, в процессе раскрутки стека, этот лидер присваивается ссылкам 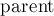
Реализовать эту операцию можно и нерекурсивно, но тогда придётся осуществлять два прохода по дереву: первый найдёт искомого лидера, второй — проставит его всем вершинам пути. Впрочем, на практике нерекурсивная реализация не даёт существенного выигрыша.
Оценка асимптотики при применении эвристики сжатия пути
Покажем, что применение одной эвристики сжатия пути позволяет достичь логарифмическую асимптотику: 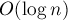
Заметим, что, поскольку операция 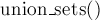
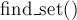

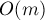
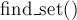
Назовём весом 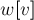

Назовём размахом ребра 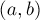
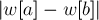
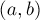
Кроме того, разобьём рёбра на классы: будем говорить, что ребро имеет класс 
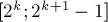
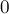
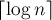
Зафиксируем теперь произвольную вершину 



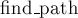

Рассмотрим работу некоторого вызова операции 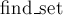
Рассмотрим этот путь и исключим из рассмотрения последнее ребро каждого класса (т.е. не более чем по одному ребру из класса 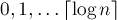
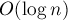
Рассмотрим теперь все остальные рёбра этого пути. Для каждого такого ребра, если оно имеет класс 


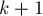
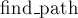
Отсюда мы окончательно получаем асимптотику работы 
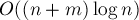
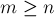
Эвристика объединения по рангу
Рассмотрим здесь другую эвристику, которая сама по себе способна ускорить время работы алгоритма, а в сочетании с эвристикой сжатия путей и вовсе способна достигнуть практически константного времени работы на один запрос в среднем.
Эта эвристика заключается в небольшом изменении работы 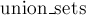
Есть два варианта ранговой эвристики: в одном варианте рангом дерева называется количество вершин в нём, в другом — глубина дерева (точнее, верхняя граница на глубину дерева, поскольку при совместном применении эвристики сжатия путей реальная глубина дерева может уменьшаться).
В обоих вариантах суть эвристики одна и та же: при выполнении 
Приведём реализацию ранговой эвристики на основе размеров деревьев:
Приведём реализацию ранговой эвристики на основе глубины деревьев:
Оба варианта ранговой эвристики являются эквивалентными с точки зрения асимптотики, поэтому на практике можно применять любую из них.
Оценка асимптотики при применении ранговой эвристики
Покажем, что асимптотика работы системы непересекающихся множеств при использовании только ранговой эвристики, без эвристики сжатия путей, будет логарифмической на один запрос в среднем: 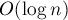
Здесь мы покажем, что при любом из двух вариантов ранговой эвристики глубина каждого дерева будет величиной 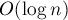
Рассмотрим ранговую эвристику по глубине дерева. Покажем, что если ранг дерева равен 
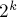
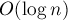
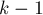

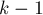
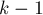

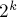
Рассмотрим теперь ранговую эвристику по размерам деревьев. Покажем, что если размер дерева равен 
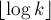
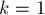
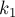
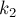
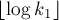
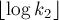
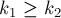
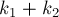
Чтобы завершить доказательство, надо показать, что:
что есть почти очевидное неравенство, поскольку 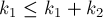
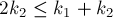
Объединение эвристик: сжатие пути плюс ранговая эвристика
Как уже упоминалось выше, совместное применение этих эвристик даёт особенно наилучший результат, в итоге достигая практически константного времени работы.
Мы не будем приводить здесь доказательства асимптотики, поскольку оно весьма объёмно (см., например, Кормен, Лейзерсон, Ривест, Штайн «Алгоритмы. Построение и анализ»). Впервые это доказательство было проведено Тарьяном (1975 г.).
Окончательный результат таков: при совместном применении эвристик сжатия пути и объединения по рангу время работы на один запрос получается 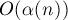
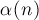

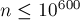
Именно поэтому про асимптотику работы системы непересекающихся множеств уместно говорить «почти константное время работы».
Приведём здесь итоговую реализацию системы непересекающихся множеств, реализующую обе указанные эвристики (используется ранговая эвристика относительно глубин деревьев):
Применения в задачах и различных улучшения
В этом разделе мы рассмотрим несколько применений структуры данных «система непересекающихся множеств», как тривиальных, так и использующих некоторые улучшения структуры данных.
Поддержка компонент связности графа
Это одно из очевидных приложений структуры данных «система непересекающихся множеств», которое, по всей видимости, и стимулировало изучение этой структуры.
Формально задачу можно сформулировать таким образом: изначально дан пустой граф, постепенно в этот граф могут добавляться вершины и неориентированные рёбра, а также поступают запросы 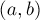


Непосредственно применяя здесь описанную выше структуру данных, мы получаем решение, которое обрабатывает один запрос на добавление вершины/ребра или запрос на проверку двух вершин — за почти константное время в среднем.
Учитывая, что практически в точности такая же задача ставится при использовании алгоритма Крускала нахождения минимального остовного дерева, мы сразу же получаем улучшенную версию этого алгоритма, работающую практически за линейное время.
Иногда на практике встречается инвертированная версия этой задачи: изначально есть граф с какими-то вершинами и рёбрами, и поступают запросы на удаление рёбер. Если задача дана в оффлайн, т.е. мы заранее можем узнать все запросы, то решать эту задачу можно следующим образом: перевернём задачу задом наперёд: будем считать, что у нас есть пустой граф, в который могут добавляться рёбра (сначала добавим ребро последнего запроса, затем предпоследнего, и т.д.). Тем самым в результате инвертирования этой задачи мы пришли к обычной задаче, решение которой описывалось выше.
Поиск компонент связности на изображении
Одно из лежащих на поверхности применений DSU заключается в решении следующей задачи: имеется изображение 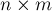
Для решения мы просто перебираем все белые клетки изображения, для каждой клетки перебираем её четырёх соседей, и если сосед тоже белый — то вызываем 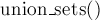
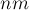
Данную задачу можно решить проще с использованием обхода в глубину (или обхода в ширину), однако у описанного здесь метода есть определённое преимущество: оно может обрабатывать матрицу построчно (оперируя только с текущей строкой, предыдущей строкой и системой непересекающихся множеств, построенной для элементов одной строки), т.е. используя порядка 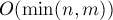
Поддержка дополнительной информации для каждого множества
«Система непересекающихся множеств» позволяет легко хранить любую дополнительную информацию, относящуюся ко множествам.
Простой пример — это размеры множеств: как их хранить, было описано при описании ранговой эвристики (информация там записывалась для текущего лидера множества).
Таким образом, вместе с лидером каждого множества можно хранить любую дополнительную требуемую в конкретной задаче информацию.
Применение DSU для сжатия «прыжков» по отрезку. Задача о покраске подотрезков в оффлайне
Одно из распространённых применений DSU заключается в том, что если есть набор элементов, и из каждого элемента выходит по одному ребру, то мы можем быстро (за почти константное время) находить конечную точку, в которую мы попадём, если будем двигаться вдоль рёбер из заданной начальной точки.
Наглядным примером этого применения является задача о покраске подотрезков: есть отрезок длины 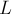

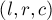
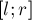

Для решения мы можем завести DSU-структуру, которая для каждой клетки будет хранить ссылку на ближайшую справа непокрашенную клетку. Таким образом, изначально каждая клетка указывает на саму себя, а после покраски первого подотрезка — клетка перед началом подотрезка будет указывать на клетку после конца подотрезка.
Теперь, чтобы решить задачу, мы рассматриваем запросы перекраски в обратном порядке: от последнего к первому. Для выполнения запроса мы просто каждый раз с помощью нашего DSU находим самую левую непокрашенную клетку внутри отрезка, перекрашиваем её, и перебрасываем указатель из неё на следующую справа пустую клетку.
Таким образом, мы здесь фактически используем DSU с эвристикой сжатия путей, но без ранговой эвристики (т.к. нам важно, кто станет лидером после объединения). Следовательно, итоговая асимптотика составит 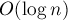
Впрочем, можно реализовать это решение с ранговой эвристикой: будем хранить для каждого множества в некотором массиве 
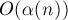
Поддержка расстояний до лидера
Иногда в конкретных приложениях системы непересекающихся множеств всплывает требование поддерживать расстояние до лидера (т.е. длину пути в рёбрах в дереве от текущей вершины до корня дерева).
Если бы не было эвристики сжатия путей, то никаких сложностей бы не возникало — расстояние до корня просто равнялось бы числу рекурсивных вызовов, которые сделала функция 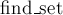
Однако в результате сжатия путей несколько рёбер пути могли сжаться в одно ребро. Таким образом, вместе с каждой вершиной придётся хранить дополнительную информацию: длину текущего ребра из вершины в предка.
При реализации удобно представлять, что массив 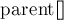
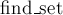
Поддержка чётности длины пути и задача о проверке двудольности графа в онлайн
По аналогии с длиной пути до лидера, так же можно поддерживать чётность длины пути до него. Почему же это применение было выделено в отдельный пункт?
Дело в том, что обычно требование хранение чётности пути всплывает в связи со следующей задачей: изначально дан пустой граф, в него могут добавляться рёбра, а также поступать запросы вида «является ли компонента связности, содержащая данную вершину, двудольной?».
Для решения этой задачи мы можем завести систему непересекающихся множеств для хранения компонент связности, и хранить у каждой вершины чётность длины пути до её лидера. Тем самым, мы можем быстро проверять, приведёт ли добавление указанного ребра к нарушению двудольности графа или нет: а именно, если концы ребра лежат в одной и той же компоненте связности, и при этом имеют одинаковые чётности длины пути до лидера, то добавление этого ребра приведёт к образованию цикла нечётной длины и превращению текущей компоненты в недвудольную.
Главная сложность, с которой мы сталкиваемся при этом, — это то, что мы должны аккуратно, с учётом чётностей, производить объединение двух деревьев в функции 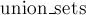
Если мы добавляем ребро 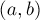


Выведём формулу, по которой должна получаться эта чётность, выставляемая лидеру одного множества при присоединении его к лидеру другого множества. Обозначим через 



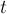





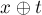
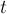
решая которое, находим:
Таким образом, независимо от того, какое множество присоединяется к какому, надо использовать указанную формулу для задания чётности ребра, проводимого из одного лидера к другому.
Приведём реализацию DSU с поддержкой чётностей. Как и в предыдущем пункте, в целях удобства мы используем пары для хранения предков и результата операции 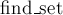
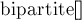
Алгоритм нахождения RMQ (минимум на отрезке) за  в среднем в оффлайне
в среднем в оффлайне
Формально задача ставится следующим образом: нужно реализовать структуру данных, которая поддерживает два вида запросов: добавление указанного числа 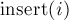
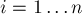
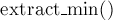
Кроме того, считаем, что вся последовательность запросов известна нам заранее, т.е. задача — в оффлайне.
Идея решения следующая. Вместо того, чтобы по очереди отвечать на каждый запрос, переберём число 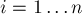
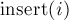

Таким образом, здесь получается идея, похожая на задачу о покраске отрезков.
Можно получить решение за 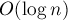
Также можно получить решение и за 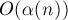
Алгоритм нахождения LCA (наименьшего общего предка в дереве) за  в среднем в оффлайне
в среднем в оффлайне
Алгоритм Тарьяна нахождения LCA за 
Хранение DSU в виде явного списка множеств. Применение этой идеи при слиянии различных структур данных
Одним из альтернативных способов хранения DSU является сохранение каждого множества в виде явно хранящегося списка его элементов. При этом, у каждого элемента также сохраняется ссылка на представителя (лидера) его множества.
На первый взгляд кажется, что это неэффективная структура данных: при объединении двух множеств мы должны будем добавить один список в конец другого, а также обновить лидера у всех элементов одного из двух списков.
Однако, как оказывается, применение весовой эвристики, аналогичной описанной выше, позволяет существенно снизить асимптотику работы: до 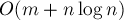


Под весовой эвристикой подразумевается, что мы всегда будем добавлять меньшее из двух множеств в большее. Добавление 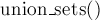
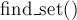

Докажем асимптотику 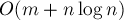



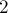

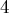

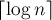
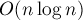

Приведём пример реализации:
Также эту идею добавления элементов меньшего множества в большее можно использовать и вне рамок DSU, при решении других задач.
Например, рассмотрим следующую задачу: дано дерево, каждому листу которого приписано какое-либо число (одно и то же число может встречаться несколько раз у разных листьев). Требуется для каждой вершины дерева узнать количество различных чисел в её поддереве.
Применив в этой задаче эту же идею, можно получить такое решение: пустим обход в глубину по дереву, который будет возвращать указатель на 
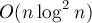
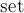
Хранение DSU с сохранением явной структуры деревьев. Переподвешивание. Алгоритм поиска мостов в графе за  в среднем в онлайне
в среднем в онлайне
Одно из мощных применений структуры данных «системы непересекающихся множеств» заключается в том, что она позволяет хранить одновременно как сжатую, так и несжатую структуру деревьев. Сжатая структура может использоваться для быстрого объединения деревьев и проверки на принадлежность двух вершин одному дереву, а несжатая — например, для поиска пути между двумя заданными вершинами, или прочих обходов структуры дерева.
При реализации это означает, что помимо обычного для DSU массива сжатых предков 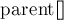
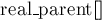
С другой стороны, при применении на практике нередко требуется научиться соединять два дерева указанным ребром, не обязательно выходящим из их корней. Это означает, что у нас нет другого выхода, кроме как переподвесить одно из деревьев за указанную вершину, чтобы затем мы смогли присоединить это дерево к другому, сделав корень этого дерева дочерней вершиной ко второму концу добавляемого ребра.
На первый взгляд кажется, что операция переподвешивания — очень затратна и сильно ухудшит асимптотику. Действительно, для переподвешивания дерева за вершину 
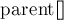
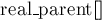
Однако на самом деле всё не так плохо: достаточно лишь переподвешивать то из двух деревьев, которое меньше, чтобы получить асимпотику одного объединения, равную 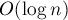
Более подробно (включая доказательства асимптотики) см. алгоритм поиска мостов в графе за 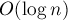
Историческая ретроспектива
Структура данных «система непересекающихся множеств» была известна сравнительно давно.
Способ хранения этой структуры в виде леса деревьев был, по всей видимости, впервые описан Галлером и Фишером в 1964 г. (Galler, Fisher «An Improved Equivalence Algorithm»), однако полный анализ асимптотики был проведён гораздо позже.
Эвристики сжатия путей и объединения по рангу, по-видимому, разработали МакИлрой (McIlroy) и Моррис (Morris), и, независимо от них, Триттер (Tritter).
Некоторое время была известна лишь оценка 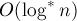
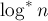
Впервые оценку 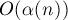
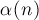
Наконец, Фредман и Сакс в 1989 г. доказали, что в принятой модели вычислений любой алгоритм для системы непересекающихся множеств должен работать как минимум за 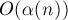
Впрочем, следует также отметить, что есть несколько статей, оспаривающих эту временную оценку и утверждающих, что система непересекающихся множеств с эвристиками сжатия пути и объединения по рангу работает за 
Задачи в online judges
Список задач, которые можно решить с помощью системы непересекающихся множеств:

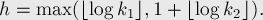
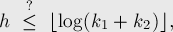
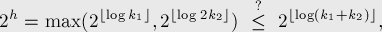
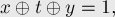
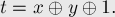
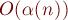 в среднем в оффлайне
в среднем в оффлайне