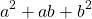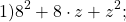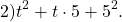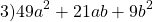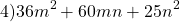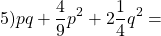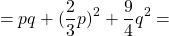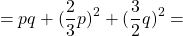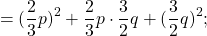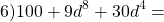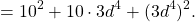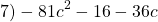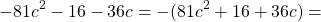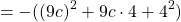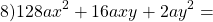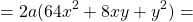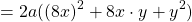Что такое неполный квадрат
Неполный квадрат разности
Неполный квадрат разности в алгебре важен в качестве составной части формулы суммы кубов. В процессе изучения формул сокращенного умножения важно научиться видеть формулы полных и неполных квадратов и различать их между собой.
Неполный квадрат разности — это сумма трех слагаемых, два из которых — квадраты некоторых выражений, а третье равно произведению этих выражений (со знаком «минус» перед ним).
В отличие от полного квадрата разности, произведение выражений не удваивается.
С помощью букв неполный квадрат разности можно записать так:
С помощью схемы — так:
Примеры неполных квадратов разности:
На практике неполный квадрат, как правило, свернут, поэтому, чтобы понять, является ли выражение неполным квадратом разности, его нужно проанализировать.
На этапе изучения новой темы есть смысл выражения подробно расписывать.
Как определить, является ли выражение неполным квадратом разности?
Признаки неполного квадрата разности
1) Выражение состоит ровно из трех слагаемых.
2) Два положительных слагаемых представляют собой квадраты некоторых выражений.
3) Третье слагаемое со знаком «минус» перед ним равно произведению этих выражений.
16x²=(4x)², 81y²=(9y)². Проверяем, равно ли третье слагаемое произведению 4x и 9y: 4x∙9y=36xy — да, равно. Следовательно, это выражение — неполный квадрат разности.
С помощью схемы это можно записать так:
100c²=(10c)², d² — уже представлен как квадрат, но 10c∙d≠20cd, поэтому выражение неполным квадратом разности не является (так как 20cd=2∙10c∙d, это выражение — полный квадрат разности).
Слагаемые могут стоять в произвольном порядке.
В некоторых случаях выражение, не являющееся неполным квадратом разности, может быть к нему приведено.
Здесь два слагаемых отрицательны, значит, неполным квадратом разности это выражение быть не может. Но если знак «минус» вынести за скобки, все знаки в скобках изменятся на противоположные:
В скобках — неполный квадрат разности.
В алгебре очень важно уметь раскладывать многочлены на множители и преобразовывать выражения (в том числе, по формуле суммы кубов, частью которой является неполный квадрат разности).
Неполный квадрат суммы
Неполный квадрат суммы в алгебре встречается в качестве составной части формулы разности кубов. Важно при преобразовании многочленов научиться видеть неполный квадрат и не путать его с полным квадратом суммы.
Неполный квадрат суммы — это сумма трех слагаемых, два из которых являются квадратами некоторых выражений, а третье равно произведению этих выражений.
У неполного квадрата суммы, в отличие от полного, произведение выражений не удваивается.
С помощью букв неполный квадрат суммы можно записать так:
Примеры неполных квадратов —
На практике квадраты и произведение записаны в свернутом виде, поэтому, чтобы понять, является ли выражение полным либо неполным квадратом суммы, его надо проанализировать. На первых шагах изучения темы формулы имеет смысл подробно расписывать, в дальнейшем — делать это устно.
Как определить, является ли некоторое выражение неполным квадратом суммы?
Признаки неполного квадрата суммы
1) Выражение состоит ровно из трех положительных слагаемых.
2) Два слагаемых представляют собой квадраты некоторых выражений.
3) Третье слагаемое равно произведению этих двух выражений.
49y²=(7y)², 9b²=(3b)². Проверяем, равно ли третье слагаемое произведению 7y и 3b: 7y∙3b=21ab — да, равно. Значит, это выражение является неполным квадратом суммы.
С помощью схемы это можно записать так:
36m²=(6m)², 25n²=(5n)². Проверяем, равно ли третье слагаемое произведению 6m и 5n: 6m∙5n=30mn≠60mn. Значит, это выражение не является неполным квадратом суммы (60mn=2∙6m∙5n, то есть здесь есть полный квадрат суммы).
Слагаемые в выражении могут стоять в произвольном порядке (не обязательно в соответствии с формулой).
Иногда выражение, не являющееся неполным квадратом суммы, может быть к нему приведено. Например,
Здесь все три слагаемые — с «-«, то есть это выражение квадратом суммы быть не может. А что, если вынести «минус» за скобки? При этом знак каждого слагаемого в скобках изменится на противоположный:
В этом случае в скобках получили неполный квадрат суммы.
В скобках получили неполный квадрат суммы.
Умение раскладывать многочлены на множители и преобразовывать выражения, в том числе, содержащие разность кубов, в алгебре — обязательно.
Формулы сокращенного умножения: таблица, примеры использования
Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.
В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.
Формулы сокращенного умножения. Таблица
Впервые тема ФСУ рассматривается в рамках курса «Алгебра» за 7 класс. Приведем ниже 7 основных формул.
Формулы сокращенного умножения
Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.
Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.
Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.
Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.
При решении практических примеров часто используют формулы сокращенного умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители.
Дополнительные формулы сокращенного умножения
Не будем ограничиваться курсом 7 класса по алгебре и добавим в нашу таблицу ФСУ еще несколько формул.
Во-первых, рассмотрим формулу бинома Ньютона.
Но что, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два? Полезной будет формула квадрата суммы трех, четырех и более слагаемых.
Как читать эту формулу? Квадрат суммы n слагаемых равен сумме квадратов всех слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Для четных показателей 2m:
Для нечетных показателей 2m+1:
Как читать формулы сокращенного умножения?
Дадим соответствующие формулировки для каждой формулы, но сначала разберемся с принципом чтения формул. Удобнее всего делать это на примере. Возьмем самую первую формулу квадрата суммы двух чисел.
Говорят: квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения выражений и квадрата второго выражения.
квадрат разности двух выражений a и b равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражения.
С учетом этого, формулы суммы и разности кубов прочитаются так:
Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.
Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.
Доказательство ФСУ
Доказать ФСУ довольно просто. Основываясь на свойствах умножения, проведем умножение частей формул в скобках.
Для примера рассмотрим формулу квадрата разности.
Чтобы возвести выражение во вторую степень нужно это выражение умножить само на себя.
Формула доказана. Остальные ФСУ доказываются аналогично.
Примеры применения ФСУ
Применим формулу суммы квадратов и получим:
Сокращаем и получаем:
Казалось бы, сложное вычисление проведено быстро всего лишь с использованием формул сокращенного умножения и таблицы умножения.
Формулы сокращённого умножения
При выполнении преобразований разных выражений часто встречаются некоторые частные случаи умножения. Равенства, выражающие эти случаи, называются формулами сокращённого умножения.
Формулы сокращённого умножения — это выражения, в которых пропущены промежуточные вычисления, поэтому их и называют сокращёнными.
Обратите внимание, что a и b в формулах сокращённого умножения могут быть как числами, так и выражениями.
Разложение формул сокращенного умножения
Рассмотрим каждую формулу подробнее и приведём доказательство верности формул сокращённого умножения.
Сумма квадратов двух чисел равна разности квадрата суммы этих чисел и их удвоенного произведения:
Доказательство: выполним преобразование правой части формулы, приведём подобные члены и получим левую часть формулы:
Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
Квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа:
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
Сумма кубов двух чисел равна произведению суммы первого и второго числа на неполных квадрат разности этих чисел:
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
Разность кубов двух чисел равна произведению разности первого и второго числа на неполный квадрат суммы этих чисел:
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
Куб суммы двух чисел равен сумме четырёх слагаемых: куб первого числа, утроенное произведение квадрата первого числа на второе число, утроенное произведение первого числа на квадрат второго и куб второго числа:
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе число, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
Неполный квадрат суммы
это квадрат суммы, которое также называется полным квадратом суммы, относительно выражения:
которое называется неполным квадратом суммы. Неполный квадрат суммы — это сумма квадратов двух чисел и их произведения. Неполный квадрат суммы отличается от полного только произведением чисел, которое не удваивается.
Неполный квадрат разности
это квадрат разности, который также называется полным квадратом разности относительно выражения:
которое называется неполным квадратом разности. Неполный квадрат разности двух чисел равен квадрату первого числа, минус произведение первого числа на второе, плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.
Формулы сокращённого умножения
Продолжаем изучать многочлены. В данном уроке мы научимся перемножать многочлены с помощью формул сокращённого умножения.
Квадрат суммы двух выражений
Выражение (2x + 3y) 2 это перемножение двух многочленов, каждый из которых равен (2x + 3y)
Получили умножение многочлена на многочлен. Выполним его:
То есть выражение (2x + 3y) 2 равно 4x 2 + 12xy + 9y 2
Решим аналогичный пример, который попроще:
Выражение (a + b) 2 это перемножение двух многочленов, каждый из которых равен (a + b)
Выполним это умножение:
То есть выражение (a + b) 2 равно a 2 + 2ab + b 2
Тождество (a + b) 2 = a 2 + 2ab + b 2 называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Первый способ:
Второй способ:
(2 + 3) 2 = 2 2 + 2 × 2 × 3 + 3 2 = 4 + 12 + 9 = 25
Пример 2. Преобразовать выражение (5a + 3) 2 в многочлен.
Воспользуемся формулой квадрата суммы двух выражений:
(5a + 3) 2 = (5a) 2 + 2 × 5a × 3 + 3 2 = 25a 2 + 30a + 9
Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:
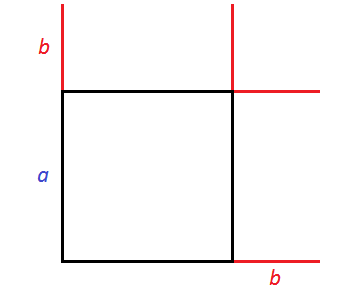
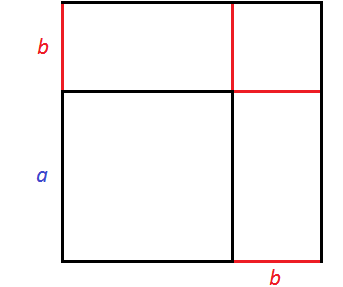
Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.
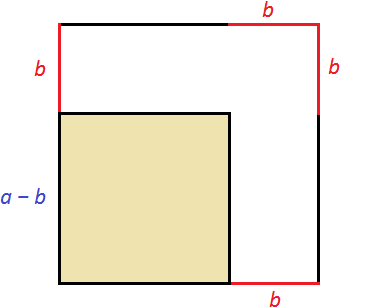
Рассмотрим следующий рисунок:
Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:
Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.
В результате получается следующая сумма площадей:
Квадрат разности двух выражений
Формула квадрата разности двух выражений выглядит следующим образом:
Эту формулу можно прочитать так:
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Формула квадрата разности двух выражений выводится таким же образом, как и формула квадрата суммы двух выражений. Выражение (a − b) 2 представляет собой произведение двух многочленов, каждый из которых равен (a − b)
Если выполнить это умножение, то получится многочлен a 2 − 2ab + b 2
Пример 1. Преобразовать выражение (7x − 5) 2 в многочлен.
Воспользуемся формулой квадрата разности двух выражений:
(7x − 5) 2 = (7x) 2 − 2 × 7x × 5 + 5 2 = 49x 2 − 70x + 25
Попробуем решить данный пример, не пользуясь формулой квадрата разности. У нас должен получиться тот же результат:
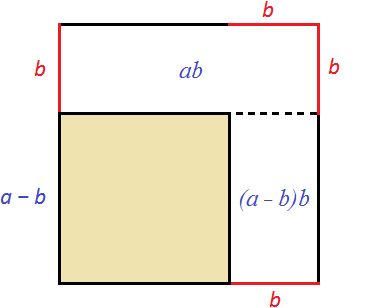
Рассмотрим следующий рисунок:
Тогда можно написать следующее выражение: старая площадь a 2 минус площадь ab минус площадь (a − b)b
Раскроем скобки в выражении (a − b)b
Приведем подобные слагаемые:
Формулы квадрата суммы и квадрата разности в общем называют формулами сокращённого умножения. Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.
Ранее мы говорили, что рассматривая член многочлена по отдельности, его нужно рассматривать вместе со знаком, который перед ним располагается.
Но применяя формулы сокращённого умножения, знак исходного многочлена не следует рассматривать в качестве знака самого этого члена.
и в таком случае нужно применять не формулу квадрата разности, а формулу квадрата суммы:
Куб суммы и куб разности
Формулы куба суммы двух выражений и куба разности двух выражений выглядят следующим образом:
Формулу куба суммы двух выражений можно прочитать так:
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
А формулу куба разности двух выражений можно прочитать так:
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
При решении задач желательно знать эти формулы наизусть. Если не запомнили — не беда! Их можно выводить самостоятельно. Мы это уже умеем.
Выведем формулу куба суммы самостоятельно:
Выражение (a + b) 3 представляет собой произведение из трёх многочленов, каждый из которых равен (a + b)
Но выражение (a + b) 3 также может быть записано как (a + b)(a + b) 2
А это есть умножение многочлена на многочлен. Выполним его:
Аналогично можно вывести формулу куба разности двух выражений:
Пример 1. Преобразуйте выражение (x + 1) 3 в многочлен.
Воспользуемся формулой куба суммы двух выражений:
(x + 1) 3 = x 3 + 3 × x 2 × 1 + 3 × x × 1 2 + 1 3 = x 3 + 3x 2 + 3x + 1
Попробуем решить данный пример, не используя формулу куба суммы двух выражений. У нас получится тот же результат, но решение станет длиннее:
Пример 2. Преобразовать выражение (6a 2 + 3b 3 ) 3 в многочлен.
Воспользуемся формулой куба суммы двух выражений:
(6a 2 + 3b 3 ) 3 = (6a 2 ) 3 + 3 × (6a 2 ) 2 × 3b 3 + 3 × 6a 2 × (3b 3 ) 2 + (3b 3 ) 3 = 216a 6 + 3 × 36a 4 × 3b 3 + 3 × 6a 2 × 9b 6 + 27b 9
Пример 3. Преобразовать выражение (n 2 − 3) 3 в многочлен.
Воспользуемся формулой куба разности двух выражений:
(n 2 − 3) 3 = (n 2 ) 3 − 3 × (n 2 ) 2 × 3 + 3 × n 2 × 3 2 − 3 3 = n 6 − 9n 4 + 27n 2 − 27
Пример 4. Преобразовать выражение (2x 2 − x 3 ) 3 в многочлен.
Воспользуемся формулой куба разности двух выражений:
Умножение разности двух выражений на их сумму
Встречаются задачи, в которых требуется умножить разность двух выражений на их сумму. Например:
В этом выражении разность двух выражений a и b умножена на сумму этих же двух выражений. Выполним данное умножение:
То есть выражение (a − b)(a + b) равно a 2 − b 2
Видим, что при умножении разности двух выражений на их сумму, получается разность квадратов этих выражений.
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Пример 1. Выполнить умножение (2x − 5)(2x + 5)
В этом примере разность выражений 2x и 5 умножена на сумму этих же выражений. Тогда согласно формуле (a − b)(a + b) = a 2 − b 2 имеем:
Вычислим правую часть, получим 4x 2 − 25
Пример 2. Выполнить умножение (4x − 5y)(4x + 5y)
Воспользуемся формулой умножения разности двух выражений на их сумму:
Пример 3. Выполнить умножение (2a + 3b)(2a − 3b)
Воспользуемся формулой умножения разности двух выражений на их сумму:
В данном примере сумма членов 2a и 3b располагалась раньше, чем разность этих членов. А в формуле (a − b)(a + b) = a 2 − b 2 разность располагается раньше.
Пример 3. Выполнить умножение (7 + 3x)(3x − 7)
Воспользуемся формулой умножения разности двух выражений на их сумму:
Пример 4. Выполнить умножение (x 2 − y 3 )(x 2 + y 3 )
Пример 5. Выполнить умножение (−5x − 3y)(5x − 3y)
Произведение (5x + 3y)(5x − 3y) заменим на разность квадратов:
Далее вычисляем выражение в скобках:
Теперь умножим −1 на выражение в скобках и получим окончательный результат:
Умножение разности двух выражений на неполный квадрат их суммы
Встречаются задачи, в которых требуется умножить разность двух выражений на неполный квадрат их суммы. Выглядит это произведение следующим образом:
Первый многочлен (a − b) является разностью двух выражений, а второй многочлен (a 2 + ab + b 2 ) является неполным квадратом суммы этих двух выражений.
Итак, умножим разность (a − b) на неполный квадрат суммы a 2 + ab + b 2
Это тождество называют формулой умножения разности двух выражений на неполный квадрат их суммы. Эту формулу можно прочитать так:
Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений.
Пример 1. Выполнить умножение (2x − 3y)(4x 2 + 6xy + 9y 2 )
Пример 2. Выполнить умножение (3 − x)(9 + 3x + x 2 )
Первый многочлен (3 − x) является разностью двух выражений, а второй многочлен является неполным квадратом суммы этих двух выражений. Это позволяет воспользоваться формулой (a − b)(a 2 + ab + b 2 ) = a 3 − b 3
Умножение суммы двух выражений на неполный квадрат их разности
Встречаются задачи, в которых требуется умножить сумму двух выражений на неполный квадрат их разности. Выглядит это произведение следующим образом:
Первый многочлен (a + b) является суммой двух выражений, а второй многочлен (a 2 − ab + b 2 ) является неполным квадратом разности этих двух выражений.
Вернёмся к изначальному примеру. Умножим сумму a + b на неполный квадрат разности a 2 − ab + b 2
Это тождество называют формулой умножения суммы двух выражений на неполный квадрат их разности. Эту формулу можно прочитать так:
Произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений.
Пример 1. Выполнить умножение (2x + 3y)(4x 2 − 6xy + 9y 2 )
Пример 2. Выполнить умножение (2x + y)(4x 2 − 2xy + y 2 )
Первый многочлен (2x + y) является суммой двух выражений, а второй многочлен (4x 2 − 2xy + y 2 ) является неполным квадратом разности этих выражений. Это позволяет воспользоваться формулой (a + b)(a 2 − ab + b 2 ) = a 3 + b 3