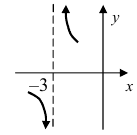
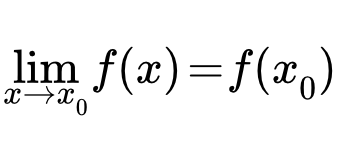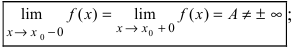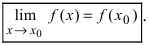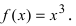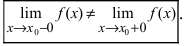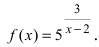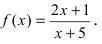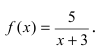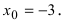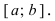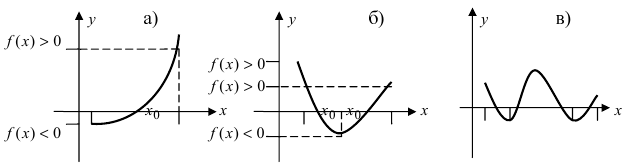Что такое непрерывная функция определение
Непрерывность функций – теоремы и свойства
Определение непрерывности функции
Определение непрерывности справа (слева)
Функция f ( x ) называется непрерывной справа (слева) в точке x 0 , если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x 0 равен значению функции в x 0 :
.
Свойства непрерывных в точке функций
Свойство непрерывности слева и справа
Функция непрерывна в точке тогда и только тогда, когда она непрерывна в справа и слева.
Доказательства свойств приводятся на странице «Свойства непрерывных в точке функций».
Непрерывность сложной функции
Предел сложной функции
Точки разрыва
Определение точки разрыва 1-го рода
Точка называется точкой разрыва первого рода, если является точкой разрыва и существуют конечные односторонние пределы слева и справа :
.
Определение скачка функции
Скачком Δ функции в точке называется разность пределов справа и слева
.
Таким образом, точка устранимого разрыва – это точка разрыва 1-го рода, в которой скачек функции равен нулю.
Определение точки разрыва 2-го рода
Точка называется точкой разрыва второго рода, если она не является точкой разрыва 1-го рода. То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.
Свойства функций, непрерывных на отрезке
Вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции
Непрерывная на отрезке функция достигает на нем своих верхней и нижней граней или, что тоже самое, достигает на отрезке своего максимума и минимума.
Обратные функции
Аналогичным образом можно сформулировать теорему о существовании и непрерывности обратной функции на полуинтервале.
Свойства и непрерывность элементарных функций
Элементарные функции и обратные к ним непрерывны на своей области определения. Далее мы приводим формулировки соответствующих теорем и даем ссылки на их доказательства.
Показательная функция
Логарифм
Экспонента и натуральный логарифм
Степенная функция
Тригонометрические функции
Теорема о непрерывности тригонометрических функций
Тригонометрические функции: синус ( sin x ), косинус ( cos x ), тангенс ( tg x ) и котангенс ( ctg x ), непрерывны на своих областях определения.
Теорема о непрерывности обратных тригонометрических функций
Обратные тригонометрические функции: арксинус ( arcsin x ), арккосинус ( arccos x ), арктангенс ( arctg x ) и арккотангенс ( arcctg x ), непрерывны на своих областях определения.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Непрерывность функции: определение, точки разрыва, примеры
Непрерывные функции образуют основной класс функций, с которыми оперирует математический анализ. Представление о непрерывной функции можно получить, если сказать, что график ее непрерывен, т.е. его можно начертить, не отрывая карандаша от бумаги.
К абстракции непрерывности человек пришел, наблюдая окружающие его, так называемые сплошные среды — твердые, жидкие или газообразные, например металлы, воду, воздух. На самом деле, как теперь хорошо известно, всякая физическая среда представляет собой скопление большого числа отделенных друг от друга движущихся частиц. Однако эти частицы и расстояния между ними настолько малы по сравнению с объемами сред, с которыми приходится иметь дело в макроскопических физических явлениях, что многие такие явления можно достаточно хорошо изучать, если считать приближенно массу изучаемой среды без всяких просветов, непрерывно распределенной в занятом ею пространстве. На таком допущении базируются многие физические дисциплины, например гидродинамика, аэродинамика, теория упругости. Математическое понятие непрерывности играет, естественно, в этих дисциплинах, как и во многих других, большую роль.
Дадим еще такое определение:
Функция называется непрерывной для всех значений, принадлежащих к данному отрезку, если она непрерывна в каждой точке этого отрезка, т.е. в каждой такой точке выполняется равенство (1).
Таким образом, для того чтобы ввести математическое определение свойства функции, заключающегося в том, что график ее есть непрерывная (в обычном понимании этого термина) кривая, появилась необходимость определить сначала локальное, местное свойство непрерывности (непрерывность в точке ), а затем на этой основе определить непрерывность функции на целом отрезке.
Приведенное определение, впервые указанное в начале прошлого столетия Коши, является общепринятым в современном математическом анализе. Проверка на многочисленных конкретных примерах показала, что это определение хорошо соответствует сложившемуся у нас практическому представлению о непрерывной функции, например представлению о непрерывном графике.
Функция может служить примером разрывной в точке функции. Ряд других примеров разрывных функций дают графики, изображенные на рис. 1.
Определение непрерывности функции
Сумма, разность и произведение конечного числа непрерывных функций есть функция непрерывная.
Точки разрыва функции
Решение. Найдем приращение функции
Решение. Для доказательства найдем приращение функции при переходе значения аргумента от к
Найдем предел приращения функции при
Так как предел приращения функции при равен нулю, то функция при непрерывна.
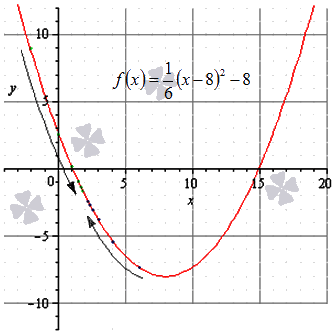
Пример 3. Определить характер разрыва функций и построить графики:
y=\operatorname
a) При функция не определена, найдём односторонние пределы в этой точки:
Следовательно, в точке функция имеет разрыв второго рода.
c) Функция определена на всей числовой оси, неэлементарная, так как в точке аналитическое выражение функции меняется. Исследуем непрерывность функции в точке :
Очевидно, что в точке функция имеет устранимый разрыв.
d) Найдём левый и правый пределы функции в точке :
Итак, в точке справа функция имеет разрыв второго рода, а слева – непрерывность.
e) Найдём односторонние пределы функции в точке :
Итак, в точке с обеих сторон у функции скачки.
Непрерывность функции в точке, разрывы первого и второго рода
Процесс исследования функции на непрерывность неразрывно связан с навыком нахождения односторонних пределов функции. Поэтому, чтобы приступить к изучению материала данной статьи, желательно предварительно разобрать тему предела функции.
Непрерывность функции в точке
Данное определение позволяет вывести следствие: значение предела функции в точках непрерывности совпадает со значением функции в этих точках.
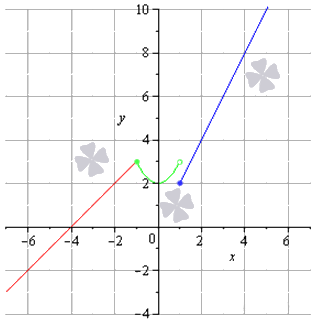
Решение
Соответствующая последовательность значений функций выглядит так:
на чертеже они обозначены зеленым цветом.
Соответствующая последовательность функций:
на рисунке обозначена синим цветом.
После вычисления значения функции в заданной точке очевидно выполнение равенства:
Устранимый разрыв первого рода
Решение
Ответ: пределы справа и слева являются равными, а заданная функция в точке х 0 = 5 не определена, т.е. в этой точке функция имеет устранимый разрыв первого рода.
Неустранимый разрыв первого рода
Неустранимый разрыв первого рода также определяется точкой скачка функции.
Решение
Определим пределы справа и слева от этих точек и значение заданной функции в этих точках:
Ответ: в конечном счете мы получили:
Нам остается только подготовить чертеж данного задания.
Разрыв второго рода (бесконечный разрыв)
Решение
Зададим произвольную последовательность значений аргумента, сходящуюся к х 0 слева. К примеру:
Ей соответствует последовательность значений функции:
Непрерывность функций и точки разрыва с примерами решения
Содержание:
Непрерывность функций и точки разрыва
Непрерывность функции
Определение: Функция
— предел функции в точке 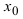
Пример:
Найти область непрерывности функции
Решение:
Данная функция непрерывна 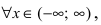
Замечание: Всякая элементарная функция непрерывна в области своего определения.
Точки разрыва
Определение: Точки, в которых не выполняется хотя бы одно из условий непрерывности функции, называются точками разрыва. Различают точки разрыва первого и второго родов.
Определение: Точкой разрыва I рода называется точка, в которой нарушается условие равенства лево- и правостороннего пределов, т.е.
Пример:
Доказать, что функция 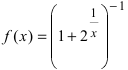
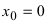
Решение:
Нарисуем график функции в окрестности нуля (Рис. 64): 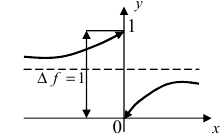
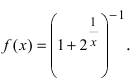
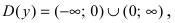
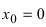
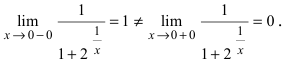
Замечание: По поводу точки разрыва I рода иначе говорят, что в этой точке функция испытывает конечный скачок (на Рис. 64 скачок равен 1).
Определение: Точка, подозрительная на разрыв, называется точкой устранимого разрыва, если в этой точке левосторонний предел равен правостороннему.
Пример:
Доказать, что функция 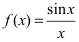
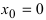
Решение:
В точке 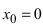
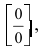
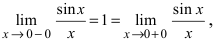
Определение: Все остальные точки разрыва называются точками разрыва II рода.
Замечание: Для точек разрыва второго рода характерен тот факт, что хотя бы
один из односторонних пределов равен 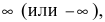
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 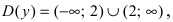
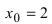
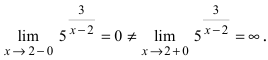
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 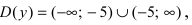
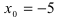
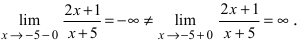
Операции над непрерывными функциями
Теорема: Сумма (разность) непрерывных функций есть непрерывная функция.
Доказательство: Докажем приведенную теорему для суммы двух функций 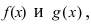
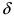
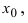
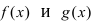
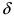
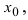
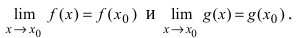
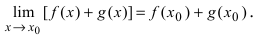
Теорема: Произведение непрерывных функций есть непрерывная функция.
Теорема: Частное двух непрерывных функций 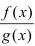
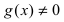
Теорема: Сложная функция от непрерывных функций есть непрерывная функция.
Схема исследования функции на непрерывность
Исследование функции на непрерывность проводят по следующей схеме:
Пример:
Исследовать на непрерывность функцию
Решение:
Согласно схеме исследования функции на непрерывность имеем:
Рис. 65. Поведение графика функции 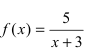
Из рисунка видно, что график функции 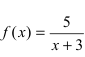
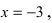
Свойства непрерывных функций на отрезке (a; b)
Свойства непрерывных функций на отрезке 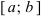
Определение: Замкнутый интервал 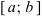
Приведем без доказательства свойства непрерывных функций на сегменте 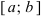
Теорема: Если функция 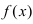
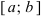
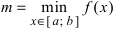
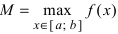
Пример:
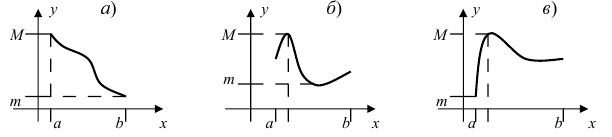
Привести примеры графиков функций, удовлетворяющих условиям теорем(см. Рис. 66).
Рис. 66. Графики функций, удовлетворяющих условиям теоремы.
Решение:
На графике а) функция достигает своего наименьшего 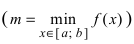
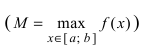
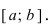
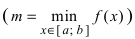
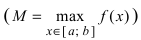
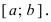
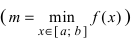
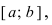
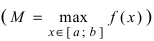
Тб. Если функция 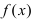
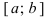
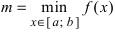
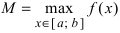
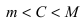
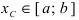
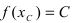
Пример:
Изобразить графики функций, удовлетворяющих условиям Тб (см. Рис. 67).
Рис. 67. Графики функций, удовлетворяющих условиям Тб.
Теорема: Если функция 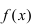
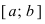
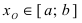
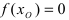
Пример:
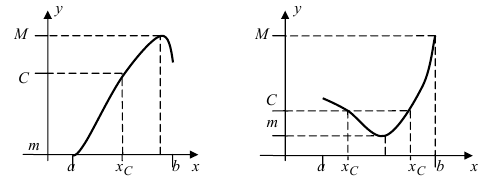
Изобразить графики функций, удовлетворяющих условиям теоремы(см. Рис. 68).
Рис. 68. Графики функций, удовлетворяющих условиям теоремы.
На графике а) существует единственная точка, в которой выполняются условия теоремы. На графиках б) и в) таких точек две и четыре, соответственно. Однако в случаях б) и в) для удовлетворения условий теоремы надо разбивать сегмент на отдельные отрезки.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.