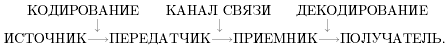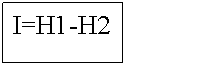Что такое непрерывная и дискретная информация
ЛЕКЦИЯ №2. Непрерывная и дискретная информация.
Перевод непрерывной в дискретную информацию. Кодирование информации.
Виды информации
Дискретная информация удобнее для обработки человеком, но непрерывная информация часто встречается в практической работе, поэтому необходимо уметь переводить непрерывную информацию в дискретную (дискретизация) и наоборот. Модем (это слово происходит от слов модуляция и демодуляция) представляет собой устройство для такого перевода: он переводит цифровые данные от компьютера в звук или электромагнитные колебания-копии звука и наоборот.
При переводе непрерывной информации в дискретную важна так называемая частота дискретизации 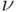
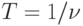
Рис. 1.1.
Чем выше частота дискретизации, тем точнее происходит перевод непрерывной информации в дискретную. Но с ростом этой частоты растет и размер дискретных данных, получаемых при таком переводе, и, следовательно, сложность их обработки, передачи и хранения. Однако для повышения точности дискретизации необязательно безграничное увеличение ее частоты. Эту частоту разумно увеличивать только до предела, определяемого теоремой о выборках, называемой также теоремой Котельникова или законом Найквиста (Nyquist).
Любая непрерывная величина описывается множеством наложенных друг на друга волновых процессов, называемых гармониками, определяемых функциями вида 
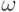
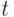
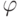
Теорема о выборках утверждает, что для точной дискретизации ее частота должна быть не менее чем в два раза выше наибольшей частоты гармоники, входящей в дискретизируемую величину 1
Примером использования этой теоремы являются лазерные компакт-диски, звуковая информация на которых хранится в цифровой форме. Чем выше будет частота дискретизации, тем точнее будут воспроизводиться звуки и тем меньше их можно будет записать на один диск, но ухо обычного человека способно различать звуки с частотой до 20КГц, поэтому точно записывать звуки с большей частотой бессмысленно. Согласно теореме о выборках частоту дискретизации нужно выбрать не меньшей 40КГц (в промышленном стандарте на компакт-диске используется частота 44.1КГц).
При преобразовании дискретной информации в непрерывную, определяющей является скорость этого преобразования: чем она выше, с тем более высокочастотными гармониками получится непрерывная величина. Но чем большие частоты встречаются в этой величине, тем сложнее с ней работать. Например, обычные телефонные линии предназначены для передачи звуков частотой до 3КГц. Связь скорости передачи и наибольшей допустимой частоты подробнее будет рассмотрена далее.
Дата добавления: 2016-03-22 ; просмотров: 4003 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Дискретные и непрерывные данные – в чем разница?
Оглавление
Для такого простого слова «данные» – довольно сложная тема. Например, «любовь» или «новости». Есть структурированные и неструктурированные данные. Тогда у вас есть качественные и количественные данные.
Теперь мы хотели бы изучить еще два типа данных – дискретный и непрерывный – и помочь вам понять разницу. (Тогда ваша организация может использовать статистическое программное обеспечение, чтобы получить представление о обоих типах.)
Чем больше вы понимаете об этих уникальных типах данных, тем больше вы сможете определить возможности, в которых каждый из них может пригодиться. Затем вы можете использовать эту информацию, чтобы принести пользу своему бренду, независимо от того, являетесь ли вы специалистом по обработке данных, аналитиком данных, инженером по обработке данных – или просто поклонником цифр.
Дискретные и непрерывные данные
В чем разница между дискретными и непрерывными данными?
Когда вы соберете набор круглых определенных чисел, они окажутся на своем месте на графике, похожем на те, что показаны слева. Дискретные данные относятся к отдельным счетным предметам.
Когда вы измеряете определенный поток данных со сложным диапазоном результатов, эти результаты будут обозначены линией в виде диапазона данных (см. Графики справа). Непрерывные данные относятся к изменениям с течением времени, включая концепции, которые не просто подсчитать, но требуют подробных измерений.
Подождите, пока мы немного раскроем эти термины для лучшего понимания.
Что такое дискретные данные?
Некоторые синонимы слова «дискретный» включают: разъединенный, отдельный и отдельный. Их можно легко применить к идее дискретных данных.
Мы собираем данные, чтобы найти взаимосвязи, тенденции и другие концепции. Например, если вы отслеживаете количество отжиманий, которые вы делаете каждый день в течение месяца, основной целью является оценка вашего прогресса и скорости улучшения.
С учетом сказанного, ваш дневной счет – это дискретное, изолированное число. Нет четкого диапазона того, сколько вы можете сделать за один день, поэтому отношения остаются неопределенными. Чем больше информации вы собираете с течением времени, тем больше идей вы можете сделать, например, что среднее количество отжиманий, которые вы делали на прошлой неделе, составляло 15 отжиманий в день, что на 5 отжиманий в день больше, чем неделей ранее. Между тем, сами числа отжиманий – это целые, круглые числа, которые нельзя разбить на более мелкие части.
Забавное практическое правило состоит в том, что во многих случаях дискретным данным может предшествовать «количество».
Примеры дискретных данных
Некоторые примеры дискретных данных, которые можно собрать:
Дискретные данные также могут быть качественными. Национальность, которую вы выбираете в форме, – это отдельные данные. Национальность каждого на вашей работе, если сгруппировать вместе с помощью программного обеспечения для работы с электронными таблицами, может быть ценной информацией при оценке вашей практики найма.
Национальная перепись состоит из дискретных данных, как качественных, так и количественных. Подсчет и сбор этой идентифицирующей информации углубляет наше понимание населения. Это помогает нам делать прогнозы о будущем, документируя историю. Это отличный пример силы дискретных данных.
Что такое непрерывные данные?
Непрерывные данные относятся к нефиксированному количеству возможных измерений между двумя реалистичными точками.
Эти числа не всегда чистые и аккуратные, как те, которые содержатся в дискретных данных, поскольку они обычно собираются на основе точных измерений. Со временем измерение определенного объекта позволяет нам создать определенный диапазон, в соответствии с которым мы можем разумно ожидать сбора большего количества данных.
Непрерывные данные – это все о точности. Переменные в этих наборах данных часто имеют десятичные точки, а число справа растянуто, насколько это возможно. Этот уровень детализации имеет первостепенное значение для ученых, врачей и производителей, и это лишь некоторые из них.
Примеры непрерывных данных
Некоторые примеры непрерывных данных включают:
Когда вы думаете об экспериментах или исследованиях, включающих постоянные измерения, они, вероятно, в некоторой степени связаны с непрерывными переменными. Если где-нибудь в таблице у вас есть число вроде «2,86290», это не то число, которое вы могли бы легко вычислить сами – подумайте об измерительных устройствах, таких как секундомеры, весы, термометры и тому подобное.
Задача с использованием этих инструментов, вероятно, применима к непрерывным данным. Например, если мы отслеживаем каждого бегуна на Олимпийских играх, время будет отображаться на графике вдоль соответствующей линии. Несмотря на то, что с годами наши спортсмены становятся быстрее и сильнее, никогда не должно быть выбросов, искажающих остальные данные. (Даже Усэйн Болт всего на пару секунд быстрее, чем историческое поле, если говорить об этом.)
На этой линии есть бесконечные возможности (например, 5,77 секунды, 5,772 секунды, 5,7699 секунды и т. Д.), Но каждое новое измерение будет постоянно находиться где-то в пределах диапазона.
Не каждый пример непрерывных данных будет аккуратно попадать в прямую линию, но со временем диапазон станет более очевидным, и вы можете сделать ставку на новые точки данных, застрявшие внутри этих параметров.
3. Формы представления информации
Сигнал называется непрерывным (или аналоговым), если его параметр может принимать любое значение в пределах некоторого интервала
Если обозначить Z- значение параметра сигнала, at- время, то зависимость Z(t) будет непрерывной функцией (рис.1.2,а).
Рис. 1.2. Непрерывные (а) и дискретные (б) сигналы
Сигнал называется дискретным, если его параметр может принимать конечное число значений в пределах некоторого интервала.
Пример дискретных сигналов представлен на рис. 1.2,б. Как следует из определения, дискретные сигналы могут быть описаны дискретным и конечным множеством значений параметров
Принципиальным и важнейшим различием непрерывных и дискретных сигналов является то, что дискретные сигналы можно обозначить, т.е. приписать каждому из конечного чисел возможные значения сигнала знак, который будет отличать данный сигнал от другого.
Вся совокупность знаков, используемых для представления дискретной информации, называется набором знаков.
Таким образом, набор есть дискретное множество знаков.
Набор знаков, в котором установлен порядок их следования, называется алфавитом.
Понятия знака и алфавита можно отнести только к дискретным сообщениям.
Так как имеются два типа сообщений, между ними, возможны четыре варианта преобразований (см. рис. 1.3):
Рис. 1.3. Варианты преобразований
Осуществимы и применяются на практике все четыре вида преобразований. Примерами устройств, в которых осуществляется преобразование типа N1 → N2 являются микрофон (звук преобразуется в электрические сигналы); магнитофон и видеомагнитофон (чередование областей намагничения ленты превращается в электрические сигналы, которые затем преобразуются в звук и изображение); телекамера (изображение и звук превращаются в электрические сигналы); радио- и телевизионный приемник (радиоволны преобразуются в электрические сигналы, а затем в звук и изображение); аналоговая вычислительная машина (одни электрические сигналы преобразуются в другие). Особенностью данного варианта преобразования является то, что оно всегда сопровождается частичной потерей информации. Потери связаны с помехами (шумами), которые порождает само информационное техническое устройство и которые воздействуют извне. Эти помехи примешиваются к основному сигналу и искажают его. Поскольку параметр сигнала может иметь любые значения (из некоторого интервала), то невозможно отделить ситуации: был ли сигнал искажен или он изначально имел такую величину. (В ряде устройств искажение происходит в силу особенностей преобразования в них сообщения, например в черно-белом телевидении теряется цвет изображения; телефон пропускает звук в более узком частотном интервале, чем интервал человеческого голоса; кино- и видеоизображение оказываются плоскими, они утратили объемность.)
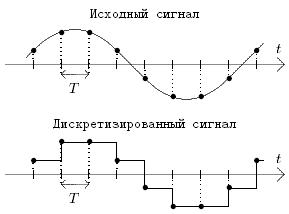
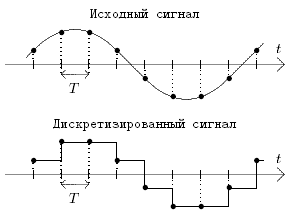
Развертка по времени состоит в том, что наблюдение за значением величины Z производится не непрерывно, а лишь в определенные моменты времени с интервалом Δt:
Совместное выполнение обеих операций эквивалентно нанесению масштабной сетки на график Z(t), как показано на рис.1.4. Далее, в качестве пар значений
Рис. 1.4. Дискретизация аналогового сигнала за счет операций развертки по времени и квантования по величине
Ответом на эти сомнения служит так называемая теорема отсчетов, доказанная в 1933г. В. А. Котельниковым (по этой причине ее иногда называют его именем), значение которой для решения проблем передачи информации было осознано лишь в 1948г. после работ К. Шеннона. Теорема, которую примем без доказательства, но результаты будем в дальнейшем использовать, гласит:
Непрерывный сигнал можно полностью отобразить и точно воссоздать по последовательности измерений или отсчетов величины этого сигнала через одинаковые интервалы времени, меньшие или равные половине периода максимальной частоты, имеющейся в сигнале.
Комментарии к теореме:
Теорема касается только тех линий связи, в которых для передачи используются колебательные или волновые процессы.
Смысл теоремы в том, что дискретизация не приведет к потере информации и по дискретным сигналам можно будет полностью восстановить исходный аналоговый сигнал, если развертка по времени выполнена в соответствии со следующим соотношением:
Можно перефразировать теорему отсчетов:
Развертка по времени может быть осуществлена без потери информации, связанной с особенностями непрерывного (аналогового) сигнала, если шаг развертки не будет превышать Δt, определяемый в соответствии с (1.2).
Например, для точной передачи речевого сигнала с частотой до Vm = 4000 Гц при дискретной записи должно производиться не менее 8000 отсчетов в секунду; в телевизионном сигнале Vm ≈ 4 МГц, следовательно, для его точной передачи потребуется около 8000000 отсчетов в секунду.
Выбор шага развертки по времени и квантования по величине сигнала лежат в основе оцифровки звука и изображения. Примерами устройств, в которых происходят такие преобразования, являются сканер, модем, устройства для цифровой записи звука и изображения, лазерный проигрыватель, графопостроитель. Термины «цифровая запись», «цифровой сигнал» следует понимать как дискретное представление с применением двоичного цифрового алфавита.
Таким образом, преобразование сигналов типа N → D, как и обратное D → N, может осуществляться без потери, содержащейся в них информации.
Таким образом, за исключением N1 → N2 в остальных случаях оказывается возможным преобразование сообщений без потерь содержащейся в них информации. При этом на первый взгляд непрерывные и дискретные сообщения оказываются равноправными. Однако на самом деле это не так. Сохранение информации в преобразованиях N → D и D → N обеспечивается именно благодаря участию в них дискретного представления. Другими словами, преобразование сообщений без потерь информации возможно только в том случае, если хотя бы одно из них является дискретным. В этом проявляется несимметричность видов сообщений и преимущество дискретной формы. К другим ее достоинствам следует отнести:
• простоту и, как следствие, надежность и относительную дешевизну устройств по обработке информации;
• точность обработки информации, которая определяется количеством обрабатывающих элементов и не зависит от точности их изготовления;
Предмет и основные разделы кибернетики
Виды информации
Дискретная информация удобнее для обработки человеком, но непрерывная информация часто встречается в практической работе, поэтому необходимо уметь переводить непрерывную информацию в дискретную ( дискретизация ) и наоборот. Модем (это слово происходит от слов модуляция и демодуляция) представляет собой устройство для такого перевода: он переводит цифровые данные от компьютера в звук или электромагнитные колебания-копии звука и наоборот.
При переводе непрерывной информации в дискретную важна так называемая частота дискретизации 
Чем выше частота дискретизации, тем точнее происходит перевод непрерывной информации в дискретную. Но с ростом этой частоты растет и размер дискретных данных, получаемых при таком переводе, и, следовательно, сложность их обработки, передачи и хранения. Однако для повышения точности дискретизации необязательно безграничное увеличение ее частоты. Эту частоту разумно увеличивать только до предела, определяемого теоремой о выборках, называемой также теоремой Котельникова или законом Найквиста (Nyquist).
Любая непрерывная величина описывается множеством наложенных друг на друга волновых процессов, называемых гармониками, определяемых функциями вида 




При преобразовании дискретной информации в непрерывную, определяющей является скорость этого преобразования: чем она выше, с тем более высокочастотными гармониками получится непрерывная величина. Но чем большие частоты встречаются в этой величине, тем сложнее с ней работать. Например, обычные телефонные линии предназначены для передачи звуков частотой до 3КГц. Связь скорости передачи и наибольшей допустимой частоты подробнее будет рассмотрена далее.
Хранение, измерение, обработка и передача информации
Бывают еще и гибридные вычислительные машины, сочетающие в себе элементы как ЦВМ, так и АВМ.
На рис.1.2 изображена схема передачи информации.
Процедуры кодирования и декодирования могут повторяться много раз. Ошибки при передаче информации происходят из-за шума в канале (атмосферные и технические помехи), а также при кодировании и декодировании. Теория информации изучает, в частности, способы минимизации количества таких ошибок.
Скорость передачи информации измеряется в количестве переданных за одну секунду бит или в бодах ( baud ): 1бод = 1бит/сек ( bps ). Производные единицы для бода такие же как и для бита и байта, например, 10Kbaud = 10240baud.
Упражнение 3 Сколько бит в одном килобайте?
Непрерывная и дискретная информация
1.2. Непрерывная и дискретная информация.
Чтобы сообщение было передано от источника к получателю, необходима некоторая материальная субстанция – носитель информации. Сообщение, передаваемое с помощью носителя, назовем сигналом. В общем случае сигнал – это изменяющийся во времени физический процесс. Такой процесс может содержать различные характеристики (например, при передаче электрических сигналов могут изменяться напряжение и сила тока). Та из характеристик, которая используется для представления сообщений, называется параметром сигнала.
В случае, когда параметр сигнала принимает последовательное во времени конечное число значений (при этом все они могут быть пронумерованы), сигнал называется дискретным, а сообщение, передаваемое с помощью таких сигналов – дискретным сообщением. Информация, передаваемая источником, в этом случае также называется дискретной. Если же источник вырабатывает непрерывное сообщение (соответственно параметр сигнала – непрерывная функция от времени), соответствующая информация называется непрерывной. Пример дискретного сообщения – процесс чтения книги, информация в которой представлена текстом, т. е. дискретной последовательностью отдельных значков (букв). Примером непрерывного сообщения служит человеческая речь, передаваемая модулированной звуковой волной; параметром сигнала в этом случае служит давление, создаваемое этой волной в точке нахождения приемника – человеческого уха.
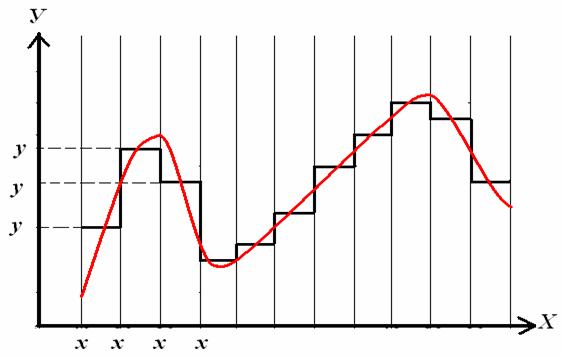
Непрерывное сообщение может быть представлено непрерывной функцией, заданной на некотором отрезке [a,b] (рис. 1.2). Непрерывное сообщение можно преобразовать в дискретное (такая процедура называется дискретизацией). Для этого из бесконечного множества значений этой функцией (параметр сигнала) выбирается их определенное число, которое приближенно может характеризовать остальные значения. Один из способов такого выбора состоит в следующем: область определения функции разбивается точками Х1, Х2 … Х на отрезке равной длинны и на каждом из этих отрезков значение функции принимается постоянным и равным, например, среднему значению на этом отрезке; полученная на этом этапе функция называется в математике ступенчатой. Следующий шаг – проецирование значений «ступеней» на ось значений функции (ось координат). Полученная таким образом последовательность значений функции Y1, Y2 … Y является дискретным представлением непрерывной функции, точность которого можно неограниченно улучшать путем уменьшения длин отрезков разбиения области значений аргумента.
Рис. 1.2. Процедура дискретизации непрерывного сообщения.
Ось значений функции можно разбить на отрезки с данным шагом и отобразить каждый из выделенных отрезков из области определения функции в соответствующий отрезок из множества значений. В итоге получим конечное множество чисел, определяемых, например, по середине или одной из границ таких отрезков.
Таким образом, любое сообщение может быть представлено как дискретное, иначе говоря, последовательностью знаков некоторого алфавита.
Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер – цифровая машина, т.е. внутреннее представление информации в нем дискретно. Дискретизация входной информации (если она непрерывна) позволяет сделать ее пригодной для компьютерной обработки.
Существуют и другие вычислительные машины – аналоговые ЭВМ. Они используются обычно для решения задач специального характера и мировой публике практически неизвестны. Эти ЭВМ в принципе не нуждаются в дискретизации входной информации, т.к. ее внутреннее представление у них непрерывно. В этом случае все наоборот – если внешняя информация дискретна, то ее «перед употреблением» необходимо преобразовать в непрерывную.
1.3. Единицы количества информации: вероятностный и объемный подходы.
Определить понятие «количество информации» довольно сложно. В решении этой проблемы существуют 2 основных подхода. Исторически они возникли почти одновременно. В конце 40-ых гг. ХХ века один из основоположников кибернетики американский математик Клод Шеннон развил вероятностный подход к измерению количества информации, а работы по созданию ЭВМ привели к «объемному» подходу.
Рассмотрим в качестве примера опыт, связанный с бросанием правильной игральной кости, имеющей N граней (наиболее распространенным является случай 6-тигранной кости: N=6). Результаты данного опыта могут быть следующие: выпали грани с одним из следующих знаков: 1, 2, …, N.
Введем в рассмотрение численную величину, измеряющую неопределенность – энтропию (обозначим ее Н). Величины N и H связаны между собой некоторой функциональной зависимостью:
А сама функция f является возрастающей, неотрицательной и определенной (в рассматриваемом нами примере) для N=1, 2, …, 6.
Рассмотрим процедуру бросания кости более подробно:
готовимся бросить кость; исход опыта неизвестен, т.е. имеется некоторая неопределенность; обозначим ее H1;
кость брошена; информация об исходе данного опыта получена; обозначим количество информации через I;
обозначим неопределенность данного опыта после его осуществления через H2;
За количество информации, которое получено в ходе осуществления опыта, примем разность неопределенностей «до» и «после» опыта:
Очевидно, что в случае, когда получен конкретный результат, имевшаяся неопределенность снята (Н2=0), и, таким образом, количество полученной информации совпадает первоначальной энтропией. Иначе говоря, неопределенность, заключенная в опыте, совпадает с информацией об исходе этого опыта.
Следующим важным моментом является определение вида функции f в формуле (1.1). Если варьировать число граней N и число бросаний кости (обозначим эту величину через М), общее число исходов (векторов длины М, состоящих из знаков 1, 2, …, М) будет равно N в степени М:
Так в случае двух бросаний кости с шестью гранями имеем: Х=62=36. Фактически каждый исход Х есть некоторая пара (Х1;Х2), где Х1 и Х2 – соответственно исходы первого и второго бросаний (общее число таких пар – Х).
Ситуацию с бросанием М раз кости можно рассматривать как некоторую сложную систему, состоящую из независимых друг от друга подсистем – «однократных бросаний кости». Энтропия такой системы в М раз больше, чем энтропия одной системы (так называемый «принцип дитивности энтропии»):
Данную формулу можно распространить и на случай любого N:
Прологарифмируем левую и правую части формулы (1.3): lnX=M*lnN, M=lnX/lnN.
Подставляем полученное для М значение в формулу (1.4):
Обозначив через К положительную константу, получим: f(x) = k*lnX, или, с учетом (1.1), H = k*lnX. Обычно принимают k=1/ln2. Таким образом
Это – формула Хартли.
Важным при введении какой – либо величины является вопрос о том, что принимать за единицу ее измерения. Очевидно, Н будет равно единице при N=2. Иначе говоря, в качестве единицы принимается количество информации, связанное с проведением опыта, состоящего в получении одного из двух равновероятных исходов (примером такого опыта может служить бросание монеты, при котором возможны 2 исхода «орел», «решка»). Такая единица количества информации называется «бит».
Все N исходов рассмотренного выше опыта являются равновероятными и поэтому можно считать, что на «долю» каждого исхода приходится одна N-я часть общей неопределенности опыта: (log2N)/N. При этом вероятность 1-го исхода Pi является, очевидно, 1/N.
Так же формула (1.6) принимается за меру энтропии в случае, когда вероятности различных исходов опыта неравновероятны (т.е. Pi могут быть различны). Формула (1.6) называется формулой Шеннона.
В качестве примера определим количество информации, связанное с появлением каждого символа в сообщениях, записанных на русском языке. Будем считать, что русский алфавит состоит из 33 букв и знака «пробел» для разделения слов. По формуле (1.5)
Однако, в словах русского языка (равно как и в словах других языков) различные буквы встречаются неодинаково часто. Ниже приведена таблица 1.1 вероятностей частоты употребления различных знаков русского алфавита, полученная на основе анализа очень больших по объему текстов.
Воспользуемся для подсчета Н формулой (1.6): Н ≈ 4,72 бит. Полученное значение Н, как и можно было предположить, меньше вычисленного ранее. Величина Н, вычисляемая по формуле (1.5), является максимальным количеством информации, которое могло бы приходиться на один знак.
| i | Символ | P(i) | i | Символ | P(i) | i | Символ | P(i) |
| 1 | пробел | 0,175 | 13 | К | 0,028 | 24 | Г | 0,012 |
| 2 | О | 0,090 | 14 | М | 0,026 | 25 | Ч | 0,012 |
| 3 | Е | 0,072 | 15 | Д | 0,025 | 26 | Й | 0,010 |
| 4 | Ё | 0,072 | 16 | П | 0,023 | 27 | Х | 0,009 |
| 5 | А | 0,062 | 17 | У | 0,021 | 28 | Ж | 0,007 |
| 6 | И | 0,062 | 18 | Я | 0,018 | 29 | Ю | 0,006 |
| 7 | Т | 0,053 | 19 | Ы | 0,016 | 30 | Ш | 0,006 |
| 8 | Н | 0,053 | 20 | З | 0,016 | 31 | Ц | 0,004 |
| 9 | С | 0,045 | 21 | Ь | 0,014 | 32 | Щ | 0,003 |
| 10 | Р | 0,040 | 22 | Ъ | 0,014 | 33 | Э | 0,003 |
| 11 | В | 0,038 | 23 | Б | 0,014 | 34 | Ф | 0,002 |
| 12 | Л | 0,035 |
H = log227 ≈ 4,76 бит
Как и в случае русского языка, частота появления тех или иных знаков неодинакова.
Если расположить все буквы данных языков в порядке убывания вероятностей, то получим следующие последовательности:
Английский язык «пробел» Е, Т, А, О, N, R,…
Немецкий язык «пробел» Е, N, I, S, T, R,…
Французский язык «пробел» E, S, A, N, I, T,…
Рассмотрим алфавит, состоящий из двух знаков 0 и 1. Если считать, что со знаками 0 и 1 в двоичном алфавите связаны одинаковые вероятности их появления (Р(О) = Р(i) = 0,5), то количество информации на один знак при двоичном кодировании будет равно
Таким образом, количество информации (в битах), заключенное в двоичном слове, равно числу двоичных знаков в нем.
В двоичной системе счисления знаки 0 и 1 будем называть битами (от английского выражения Binary digits – двоичные цифры). Отметим, что создатели компьютеров отдают предпочтение именно двоичной системе счисления потому, что в техническом устройстве наиболее просто реализовать два противоположных физических состояния: некоторый физический элемент, имеющий 2 различных состояния: намагниченность в двух противоположных направлениях; прибор, пропускающий или нет электрический ток; конденсатор, заряженный или незаряженный и т. п. В компьютере бит является наименьшей возможной единицей информации. Объем информации, записанной двоичными знаками в памяти компьютера или на внешнем носителе информации подсчитывается просто по количеству требуемых для такой записи двоичных символов. При этом, в частности, невозможно нецелое число битов (в отличии от вероятностного подхода).
Для удобства использования введены более крупные, чем бит, единицы количества информации. Так, двоичное слово из восьми знаков содержит один байт информации, 1024 бита образуют килобайт (Кбайт), 1024 килобайта – мегабайт (Мбайт), а 1024 мегабайта – гигабайт (Гбайт).
Между вероятностным и объемным количеством информации соотношение не однозначное. Далеко не всякий текст, записанный двоичными символами, допускает измерение объема информации в кибернетическом смысле, но заведомо допускают его в объемном. Далее, если некоторое сообщение допускает измеримость количества информации в обоих смыслах, то они не обязательно совпадают, при этом кибернетическое количество информации не может быть больше объемного.
В дальнейшем тексте данного учебника практически всегда количество информации помещается в объемном смысле.