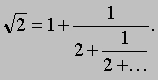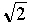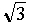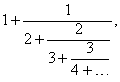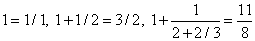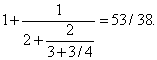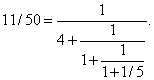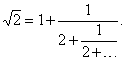Что такое непрерывные дроби

НЕПРЕРЫВНЫЕ ДРОБИ

Полезное

Смотреть что такое «НЕПРЕРЫВНЫЕ ДРОБИ» в других словарях:

Периодические непрерывные дроби — см. Дробь … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Натуральный логарифм — График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0 («медленно» и «быстро» по сравнению с любой степенной… … Википедия

История арифметики — Арифметика. Роспись Пинтуриккьо. Апартаменты Борджиа. 1492 1495. Рим, Ватиканские дворцы … Википедия

История математики в Индии — Данная статья часть обзора История математики. Научные достижения индийской математики широки и многообразны. Уже в древние времена учёные Индии на своём, во многом оригинальном пути развития достигли высокого уровня математических знаний.… … Википедия

ДИОФАНТОВЫ ПРИБЛИЖЕНИЯ — раздел теории чисел, в к ром изучаются приближения нуля значениями функций от конечного числа целочисленных аргументов. Первоначальные задачи Д. п. касались рациональных приближений к действительным числам, но развитие теории привело к задачам, в … Математическая энциклопедия

История математики — История науки … Википедия

Математика исламского средневековья — Данная статья часть обзора История математики. Арабский халифат (750 г.) Математика Востока, в отличие от древнегреческой математики, в … Википедия

Чебышев, Пафнутий Львович — (родился 14 мая 1821 года умер 26 ноября 1894 года в Петербурге) ординарный академик Императорской Академии Наук, действительный тайный советник. П. Л. Чебышев, профессор императорского С. Петербургского университета Тайный советник, доктор… … Большая биографическая энциклопедия

Математика в Древней Греции — Данная статья часть обзора История математики. Муза геометрии (Лувр) … Википедия

Математика в Древнем Египте — Данная статья часть обзора История математики. Статья посвящена состоянию и развитию математики в Древнем Египте в период примерно с XXX по III век до н. э. Древнейшие древнеегипетские математические тексты относятся к началу II… … Википедия

Источник

НЕПРЕРЫВНЫЕ ДРОБИ

НЕПРЕРЫВНЫЕ ДРОБИ. Последовательность, каждый член которой является обычной дробью, порождает непрерывную (или цепную) дробь, если ее второй член прибавить к первому, а каждую дробь, начиная с третьей, прибавить к знаменателю предыдущей дроби.

Например, последовательность 1, 1/2, 2/3, 3/4. n/(n + 1). порождает непрерывную дробь

где многоточие в конце указывает на то, что процесс продолжается бесконечно. В свою очередь непрерывная дробь порождает другую последовательность дробей, называемых подходящими. В нашем примере первая, вторая, третья и четвертая подходящие дроби равны

Их можно построить по простому правилу из последовательности неполных частных 1, 1/2, 2/3, 3/4. Прежде всего выпишем первую и вторую подходящие дроби 1/1 и 3/2. Третья подходящая дробь равна (2 Ч 1 + 3 Ч 3)/(2 Ч 1 + 3 Ч 2) или 11/8, ее числитель равен сумме произведений числителей первой и второй подходящих дробей, умноженных соответственно на числитель и знаменатель третьего неполного частного, а знаменатель равен сумме произведений знаменателей первого и второго неполных частных, умноженных соответственно на числитель и знаменатель третьего неполного частного. Четвертая подходящая дробь получается аналогично из четвертого неполного частного 3/4 и второй и третьей подходящих дробей: (3 Ч 3 + 4 Ч 11)/(3 Ч 2 + 4 Ч 8) или 53/38. Следуя этому правилу, находим первые семь подходящих дробей: 1/1, 3/2, 11/8, 53/38, 309/222, 2119/1522 и 16687/11986. Запишем их в виде десятичных дробей (с шестью знаками после запятой): 1,000000; 1,500000; 1,375000; 1,397368; 1,391892; 1,392247 и 1,392208. Значением нашей непрерывной дроби будет число x, первые цифры которого 1,3922. Подходящие дроби являются лучшим приближением числа x. Причем они поочередно оказываются то меньше, то больше числа x (нечетные – больше x, а четные – меньше).

Чтобы представить отношение двух положительных целых чисел в виде конечной непрерывной дроби, нужно воспользоваться методом нахождения наибольшего общего делителя. Например, возьмем отношение 50/11. Так как 50 = 4 Ч 11 + 6 или 11/50 = 1/(4 + 6/11), и, аналогично, 6/11 = 1/(1 + 5/6) или 5/6 = 1/(1 + 1/5), получаем:

Непрерывные дроби используются для приближения иррациональных чисел рациональными. Предположим, что x – иррациональное число (т.е. непредставимо в виде отношения двух целых чисел). Тогда, если n₀ – наибольшее целое число, которое меньше x, то x = n₀ + (x – n₀), где x – n₀ – положительное число меньше 1, поэтому обратное ему число x₁ больше 1 и x = n₀ + 1/x₁. Если n₁ – наибольшее целое число, которое меньше x₁, то x₁ = n₁ + (x₁ – n₁), где x₁ – n₁ – положительное число, которое меньше 1, поэтому обратное ему число x₂ больше 1, и x₁ = n₁ + 1/x₂. Если n₂ – наибольшее целое число, которое меньше x₂, то x₂ = n₂ + 1/x₃, где x₃ больше 1, и т.д. В результате мы шаг за шагом находим последовательность неполных частных n₀, 1/n₁, 1/n₂. непрерывной дроби, являющихся приближениями x.

Поясним сказанное на примере. Предположим, что 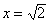, тогда

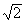
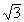
Первые 6 подходящих дробей равны 1/1, 3/2, 7/5, 17/12, 41/29, 99/70. Записанные в виде десятичных дробей они дают следующие приближенные значения : 1,000; 1,500; 1,400; 1,417; 1,4137; 1,41428. Непрерывная дробь для имеет неполные частные 1, 1/1, 1/2, 1/1, 1/2, 1/1. Иррациональное число является корнем квадратного уравнения с целочисленными коэффициентами в том и только в том случае, если неполные частные его разложения в непрерывную дробь периодичны.

Источник

Исследовательский проект по математике Непрерывные дроби

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

История появления и развития непрерывных дробей

Применение непрерывных дробей в теории чисел

Применение непрерывных дробей в аналитической теории

Приложения непрерывных дробей

В вычислительной практике действительные числа заменяют рациональными, при этом рациональное число выбирают максимально простым в виде десятичной дроби с небольшим числом знаков после запятой или обыкновенной с небольшим знаменателем. В вопросах приближённого представления действительных чисел рациональными дробями большое значение имеет аппарат непрерывных (цепных) дробей.

Бесконечной цепной, или непрерывной, дробью общего вида называют разложение

где и могут принимать произвольные, отличные от нуля рациональные значения, может быть равно нулю. Если в данной дроби все , (), то дробь будет называться правильной цепной дробью.

Также различают ветвящиеся непрерывные дроби:

Дроби такого вида широко применяются во многих вопросах вычислительной математики.

В своей основе вопросы теории непрерывных дробей доступны учащимся основной школы. Её алгоритмы основаны на применении алгоритма Евклида, выделения целой части числа. Её задачи связаны с аппроксимацией действительных чисел и опираются на теорию рациональных и действительных чисел.

Цель проекта – изучить непрерывные дроби общего вида, рассмотреть возможные способы аппроксимации действительных чисел рациональными дробями и выбрать оптимальный, дающий наилучшие приближения.

1. рассмотреть вопросы истории, касающиеся появления и развития непрерывных дробей, а также их приложений;

2. овладеть алгоритмами нахождения подходящих дробей для действительных чисел;

3. изучить основные свойства подходящих дробей цепной дроби;

4. рассмотреть различные способы оценки погрешности, возникающие при аппроксимации действительных чисел рациональными дробями;

5. подобрать примеры для иллюстрации теоретических положений.

1. История появления и развития непрерывных дробей

По некоторым сведениям непрерывные дроби применялись уже математиками Древней Греции. Например, алгоритм Евклида (III в. до н.э.) тесно связан с цепными дробями. Возможно, что при нахождении приближения к числу Архимед (ок. 287-212 до н.э.) пользовался методом, близкому к разложению в цепную дробь.

Известно, что китайский астроном ЦзуЧун-чжи (V в. н.э.) показал, что π заключено между 3,1415926 и 3,1415927. он указал в качестве рационального приближения к π величину .

Из средневековых математиков близко подошёл к цепным дробям Омар Хайям (ок. 1048-1122). Он положил их в основу своей идеи реформы календаря. Продолжительность года по его приближениям составляла суток и составляла погрешность всего 19 секунд в год [4].

Но впервые непрерывные дроби как таковые появляются в «Алгебре» итальянского математика Рафаэль Бомбелли (1526-1572), вышедший в 1572 г. в статье, написанной в то время, когда в Италии и Франции впервые появились алгебраические понятия и обозначения. Бомбелли пришёл к цепным дробям, изучая извлечение квадратного корня из чисел. Первым известным использованием непрерывной дроби является приближённое выражение для следующего вида . Это частный случай формулы .

Следующее по времени применение цепной дроби, причём опять-таки к извлечению квадратных корней принадлежит итальянскому математику Пьетро Антонио Катальди (1552-1626), им был предложен второй частный случай данной формулы: . В 1613 г. он ввёл при записи цепной дроби повторное применение дробной черты, т.е. уже настоящее обозначение цепной дроби, только вместо + он употреблял перлюэт (&), т.е. сокращённое обозначение латинского союза et (и). И его запись разложения выглядела следующим образом: =4&&… Кроме разложения иррационального числа в ряд Катальди ещё и нашёл приближения этого числа: и , между которыми заключён (хотя он не знал способа последовательного вычисления подходящих дробей). При этом Катальди заметил, что значение цепной дроби всегда заключено между соседними подходящими дробями.

В середине XVII века английский математик Джон Валлис (1616-1703) первым по времени разложил трансцендентное число в бесконечное произведение: …, а У. Броункер (1620-1686), первый президент Королевского общества, около 1659 г. без доказательства опубликовал разложение его в цепную дробь: .

Следующий шаг в развитии теории непрерывных дробей был сделан Христианом Гюйгенсом (1629-1695). Он строил модель солнечной системы с помощью набора зубчатых колес. По расчетам оказалось, что отношение числа зубцов двух каких-либо колёс должно быть равным отношению времён обращения двух планет вокруг Солнца. Это отношение выражается достаточно точно в виде (несократимой) дроби с большим числителем и большим знаменателем. Изготовление же таких зубчатых колёс, практически очень сложно. Тогда Гюйгенс нашёл среди дробей с меньшим числителем и меньшим знаменателем подходящую дробь к числу . Как и Швентер, Гюйгенс решил эту задачу посредством разложения обыкновенной дроби в цепную дробь и поэтому ограничился рассмотрением правильных непрерывных дробей. Благодаря чему была найдена подходящая дробь , аппроксимирующая дробь с большими числителем и знаменателем, и имеющая погрешность, которая составляет лишь десятитысячную долю от единицы.Гюйгенс обратил внимание на то, что нельзя найти обыкновенную дробь с меньшими числителем и знаменателем, чем подходящая, которая была бы ближе к значению цепной дроби; а также, что подходящие дроби попеременно то больше, то меньше значения цепной дроби.

Можно сказать, что цепными дробями занимались от случая к случаю, и первым, кто систематизировал знания о непрерывных дробях и изложил полную их теорию, насколько это было возможно сделать в ту эпоху, был Леонард Эйлер (1707-1783). Он опубликовал свою первую работу в 1744 г., в которой рассматривал цепную дробь общего вида и впервые появляются соответствующие непрерывные дроби. Следует заметить, что сам термин «цепная дробь» появился лишь в XVIII веке, а до этого времени использовалось понятие «непрерывная дробь». Вторая работа Эйлера, вышедшая в 1750 г., фактически являлась её продолжением, в ней рассматривались вопросы о применении непрерывных дробей для решения дифференциальных уравнений, алгоритм нахождения подходящих дробей, преобразование числовых рядов в равноценные непрерывные дроби, представление иррациональных чисел в непрерывные дроби и нахождение для некоторых из них подходящих дробей. Из его работ стало ясно, что непрерывные дроби могут применяться как в теории чисел, так и в анализе. Эйлеру также принадлежат и многие другие работы, связанные с изучением и применением непрерывных дробей.

2. Применение непрерывных дробей в теории чисел

Задачами, относящимися к теории чисел, являются разложения действительных чисел в правильные непрерывные дроби и аппроксимации действительных чисел с помощью непрерывных (непрерывных) дробей. Здесь наиболее важным является вопрос о степени приближения, которое обеспечивает n-я подходящая дробь и об оценке погрешности при замене действительного числа подходящей дробью.

Эварист Галуа (1811-1832) в своей первой опубликованной работе исследовал некоторые периодические правильные непрерывные дроби. Он дал определение двойственных периодических правильных непрерывных дробей.

Жозеф Лиувилль (1809-1882) первым доказал существование трансцендентных чисел. В 1851 г. он отметил, что алгебраические числа не могут быть достаточно точно аппроксимированы рациональными числами. Он доказал, что для — корня неприводимого полинома с целыми коэффициентами степени n существует константа с: 0

Результат, полученный Адольф Гурвицем (1859-1919) в 1891 заключается в том, что неравенство всегда имеет бесконечное число рациональных решений . Эмиль Борель (1871-1956) дал простое доказательство этого факта, заметив, что среди любых трёх следующих одна за другой последующих дробей правильного непрерывно-дробного разложения имеется хотя бы одна, которая удовлетворяет данному неравенству.

Оттенок теории меры придали этим результатам Борель и Феликс Бернштейн (1878-1956), которые доказали, что для почти всех х: 0

3 Применение непрерывных дробей в аналитической теории

Значительный вклад в аналитическую теорию внёс Эйлер. Им были получены разложения в непрерывные дроби для интегралов и степенных рядов, включая и расходящиеся, а также показал, как разложение Броункера для может быть выведено либо из формулы приведения Валлиса, либо из знакопеременного ряда Грегори – Лейбница для. Другим вкладом Эйлера было решение дифференциального уравнения Риккати при помощи непрерывных дробей. В аналитическом направлении теории непрерывных дробей работали Иоганн Генрих Ламберт (1728-1777) (разложил в непрерывные дроби ln(1+x), arctgx и tgx ; и полностью исследовал вопросы сходимости непрерывных дробей к этим функциям), Лагранж, Гаусс, Карл Густав Якоби (1804-1851). Девятнадцатый век стал временем бурного развития аналитической теории непрерывных дробей. Методы непрерывных дробей использовались при изучении специальных функций, для нахождения конкретных численных результатов. В области теории разложения и сходимости непрерывных дробей, элементами которых являются линейные функции комплексного переменного, работали такие математики, как Пьер Симон Лаплас, Лежандр, Якоби, Эйзенштейн, Лаггер, Бернхард Риман (1826-1866), Томас Иоаннес Стилтьес, П.Л. Чебышев (1821-1894), Фробениус (1849-1917) и Анри Пуанкаре (1854-1912). Эти исследования оказали далеко идущее влияние на дальнейшее развитие математики. Особенно это относится к работам Стилтьеса, которые привели к таким важным исследованиям, как проблема моментов, теория интеграла Стилтьеса, начало систематического изучения сходимости последовательностей голоморфных функций и первое применение Гильбертом и его школой аппарата спектральной теории самосопряжённых операторов в гильбертовом пространстве к проблеме моментов. В работах Пуанкаре и Стилтьеса, в которых разложения в непрерывные дроби применялись в связи с расходящимися рядами, по-видимому, впервые появились асимптотические разложения.

Методы, разработанные Фробениусом и Паде в конце XIX века для приближения аналитических функций подходящими дробями непрерывных дробей под общим названием аппроксимаций Паде, стали главным вычислительным средством в задачах статистической механики и физики твёрдого тела, быстро распространяясь на другие разделы теоретической физики.

Гейне в 1846-1847 гг. занимался гипергеометрическими функциями. Проблемой сходимости непрерывных дробей для отношений этих функций – Риман, и более полно этот вопрос был рассмотрен Томе. Решение задача представления произвольных степенных рядов цепными дробями было начато Штерном в 1832 г. и Хейлерманом в 1846 и продолжено Фробениусом и Стилтьесом. Интерес к этой теме проявляли многие математики, их работы играли большую роль для науки. Ею также активно занимались и русские учёные: в XIX веке работы П.Л. Чебышева, А.А.Маркова (1856-1922), И.В.Слешинского и других математиков внесли значительный вклад в теорию непрерывных дробей.

В Марийском педагогическом институте под руководством А.Н.Хованского в 50-60-е годы XX века работала аспирантура, в которой занимались исследованием аналитических вопросов непрерывных дробей. В последствии успешно защитили кандидатские диссертации и опубликовали ряд работ Г.В. Маурер, Л.П. Шутова, C.С. Хлопонин, В.К. Смышляев.

Таким образом, благодаря систематическому изучению Эйлером непрерывных дробей, многие математики, работающие в России и за её пределами, заинтересовались этим вопросом и продолжили его изучение в своих работах. Огромное количество работ, посвящённых теории непрерывных дробей, говорит о широких возможностях применения её к различным областям науки.

4 Приложения непрерывных дробей

Непрерывные и ветвящиеся непрерывные дроби обладают рядом уникальных свойств, обеспечивающих им широкое использование в теоретической и прикладной математике. Этим и объясняется повышенный интерес математиков к данной теории на протяжении нескольких веков.

В настоящее время в теоретическом плане непрерывные дроби играют существенную роль, так как позволяют усилить и развить результаты классической математики на случай многих аргументов, причём сам аппарат непрерывных дробей зачастую подсказывает формулировки такого рода обобщений, в частности, в теории чисел.

Непрерывные дроби широко применяются в теории чисел: обобщены некоторые основные алгоритмы (алгоритм Евклида, Остроградского, Эйлера), найдено решение классической задачи об алгебраических иррациональностях высших степеней, найдены отдельные решения некоторых диофантовых уравнений и их систем.

Непрерывные дроби дают большое преимущество в точности при приближённом нахождении корней квадратных уравнений; вычислении логарифмов чисел.

Непрерывные дроби позволяют строить алгоритмы для вычисления корней алгебраических уравнений произвольной степени. В вычислительной практике используются при решении сравнений первой степени, также удобны в использовании дробно-рациональные аппроксимации функций одного аргумента цепными дробями с помощью формул Обрешкова или Тиле по методу Паде. Они также используются в теории сравнений.

На базе непрерывных дробей построены некоторые эффективные методы решения алгебраических и трансцендентных уравнений, неопределённых уравнений вида , , уравнений рекуррентного типа, и других типов уравнений. Решение задачи Коши для линейных систем дифференциальных уравнений с частными производными можно представить ветвящимися цепными дробями, при наложении некоторых условий к системе и начальным условиям.

Непрерывные дроби используются для нахождения приближенных представлений функций. Эти приближения, являющиеся дробно-рациональными функциями от независимых переменных успешно заменяют данную функцию в тех областях изменения аргумента, где, например, разложение этой функции в степенной ряд расходится и где, следовательно, приближения в виде многочленов в большинстве случаев неприменимы. При использовании дробно-рациональных приближений отпадает необходимость вычислять высокие степени аргумента и появляется возможность вычислять значения отдельных функций.

Теория матричных ветвящихся непрерывных дробей позволяет решить следующие задачи: извлечение квадратного корня, корня третьей, четвёртой степени и корня любой рациональной степени с помощью матриц, решение уравнений с помощью матриц второго порядка, решение уравнений высших степеней с помощью матриц. (Матричные рекуррентные уравнения применяются в задачах экономики, физики, плазмы и др.)

В настоящее время непрерывные дроби находят всё большее применение в вычислительной технике, так как позволяют строить эффективные алгоритмы для решения ряда задач на ЭВМ.

Помимо теоретического использования правильных непрерывных дробей существуют и практические приложения непрерывных дробей. Среди всего их множества можно отметить следующие:

1.Решение обратных задач теплопроводности;

2.Исследование механических колебаний в валопроводах различных энергетических установок;

3.Синтез устройств частотной селекции на функциональных времязадающих элементах;

4.Исследование устойчивости, исследование установившихся и переходных процессов, стабилизация систем, исследование и обеспечение качества систем, исследование случайных процессов, оптимизация параметров и ряд других проблем в технике, в частности, в автоматике, радиоэлектронике, приборостроении и др.

Источник