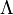Что такое непустое множество
Пустое множество
Пусто́е мно́жество (в математике) — множество, не содержащее ни одного элемента. Из аксиомы объёмности следует, что есть только одно множество, обладающее таким свойством. Пустое множество является своим (тривиальным) подмножеством, но не является своим элементом.
Пустое множество является конечным множеством и имеет наименьшую мощность среди всех множеств. Пустое множество — единственное множество, для которого класс множеств, равномощных ему, состоит из единственного элемента (самого́ пустого множества). Также, пустое множество — единственное множество, имеющее ровно 1 подмножество (само себя), и единственное множество, равномощное любому своему подмножеству.
Пустое множество тривиальным образом является разрешимым (а значит, перечислимым и арифметическим), транзитивным (англ.) и вполне упорядоченным множеством (для любого отношения порядка). Пустое множество является наименьшим порядковым числом и наименьшим кардинальным числом. В топологии, пустое множество является одновременно замкнутым и открытым множеством.
-цепочка, начинающаяся с произвольного множества, каждый последующий член которой является элементом предыдущего, всегда через конечное число шагов завершается пустым множеством (см. аксиому регулярности). Таким образом, пустое множество является «строительным кирпичиком», из которого строятся все остальные множества.
В некоторых формулировках теории множеств существование пустого множества постулируется (см. аксиому пустого множества), в других — доказывается.
Содержание
Обозначения пустого множества
Обычно пустое множество обозначают одним из следующих символов: 
, 
и 
.
Реже пустое множество обозначают одним из следующих символов: 
и 
.
В Юникоде имеется специальный символ «пустое множество» (U+2205, ∅ ).
Символы и введены в употребление группой Бурбаки (в частности, Андре Вейлем) в 1939 году.
Свойства пустого множества
См. также
Ссылки
Полезное
Смотреть что такое «Пустое множество» в других словарях:
пустое множество — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN empty set … Справочник технического переводчика
пустое множество — понятие теории множеств; пустое множество множество, не содержащее ни одного элемента; обозначается ø или 0. Понятие пустое множество (подобно понятию «нуль») возникает из потребности, чтобы результат всякой операции над множествами был также… … Энциклопедический словарь
пустое множество — tuščioji aibė statusas T sritis automatika atitikmenys: angl. empty set vok. Leerensemble, n rus. пустое множество, n pranc. ensemble vide, m … Automatikos terminų žodynas
Пустое множество — (математическое) «множество», не содержащее ни одного элемента. Понятие «П. м.» (подобно понятию «нуль»; возникает из потребности, чтобы результат всякой операции над множествами был также множеством (см. Множеств теория). Источником… … Большая советская энциклопедия
ПУСТОЕ МНОЖЕСТВО — понятие теории множеств; П. м. множество, не содержащее ни одного элемента; обозначается 0. Понятие П. м. (подобно понятию нуль ) возникает из потребности, чтобы результат всякой операции над множествами был также множеством … Естествознание. Энциклопедический словарь
Множество — У этого термина существуют и другие значения, см. Множество (значения). Запрос «Целое» перенаправляется сюда; о типе данных в программировании см. Целое (тип данных). Множество одно из ключевых понятий математики, в частности, теории… … Википедия
Множество (тип данных) — У этого термина существуют и другие значения, см. Множество (значения). Множество тип и структура данных в информатике, является реализацией математического объекта множество. Данные типа множество позволяют хранить ограниченное число значений… … Википедия
Множество (математика) — Множество один из ключевых объектов математики, в частности, теории множеств. «Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли» (Г. Кантор). Это не является в полном… … Википедия
Непустое множество
Пустым множеством в математике называется множество, не содержащее ни одного элемента.
В одних теориях множеств существование [по меньшей мере одного] пустого множества провозглашается (см. аксиому пустого множества), в других — доказывается. Во всех теориях множеств единственность пустого множества доказывается (см. аксиому объёмности).
Содержание
Обозначения пустого множества
Обычно пустое множество обозначают одним из следующих символов: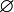 
, 
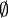
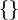
и 
.
Реже пустое множество обозначают одним из следующих символов: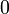 
и 
В Юникоде имеется специальный символ «пустое множество» (U+2205, ∅ ).
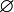
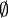
Символы и введены в употребление группой Бурбаки (в частности, Андре Вейлем) в 1939 году.
Символ 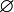идентичен букве Ø в Датско-норвежском алфавите. [1]
Свойства пустого множества
См. также
Ссылки
Полезное
Смотреть что такое «Непустое множество» в других словарях:
Множество — У этого термина существуют и другие значения, см. Множество (значения). Запрос «Целое» перенаправляется сюда; о типе данных в программировании см. Целое (тип данных). Множество одно из ключевых понятий математики, в частности, теории… … Википедия
ЧАСТИЧНО УПОРЯДОЧЕННОЕ МНОЖЕСТВО — непустое множество, на к ром зафиксирован нек рый порядок. Ч. у. м. является примером модели. Примеры Ч. у. м.: 1) множество натуральных чисел с обычным порядком; 2) множество натуральных чисел, где означает, что аделит b; 3) множество всех… … Математическая энциклопедия
Направленное множество — В математике, направленным множеством называется непустое множество A с заданным на нем рефлексивным транзитивным отношением ≤ (т. е. предпорядком), обладающее дополнительным свойством: для любых двух элементов из A найдется элемент из A… … Википедия
ПРОЕКТИВНОЕ МНОЖЕСТВО — множество, к рое может быть получено из борелевских множеств повторным применением операций проектирования и перехода к дополнению. П. м. классифицируются по классам, образующим проективную иерархию. Пусть I=ww бэровское пространство… … Математическая энциклопедия
Частично упорядоченное множество — У этого термина существуют и другие значения, см. Упорядоченное множество. Подмножества
Нечёткое множество — Эту страницу предлагается объединить с Теория нечётких множеств … Википедия
Нечеткое множество — Нечёткое (или размытое, расплывчатое, туманное, пушистое) множество понятие, введённое Лотфи Заде в 1965 г. в статье «Fuzzy Sets» (нечёткие множества) в журнале Information and Control [1]. Л. Заде расширил классическое канторовское понятие… … Википедия
Пушистое множество — Нечёткое (или размытое, расплывчатое, туманное, пушистое) множество понятие, введённое Лотфи Заде в 1965 г. в статье «Fuzzy Sets» (нечёткие множества) в журнале Information and Control [1]. Л. Заде расширил классическое канторовское понятие… … Википедия
Что такое непустое множество
Излагаются практически важные разделы аппарата современной математики, которые используются в инженерном деле: множества, матрицы, графы, логика, вероятности. Теоретический материал иллюстрируется примерами из различных отраслей техники. Предназначена для инженерно-технических работников и может быть полезна студентам ВУЗов соответствующих специальностей.
Математический аппарат инженера
1. Математика в инженерном деле
Задачи и упражнения
Задачи и упражнения.
Задачи и упражнения
Задачи и упражнения
Задачи и упражнения
1. Алгебра множеств
1. Логические функции
6. Конечные автоматы
Математический аппарат инженера
Сегодня трудно назвать область науки, промышленности и народного хозяйства, где бы не использовались математические модели. Это стало возможным благодаря совместным усилиям математиков, работавших в абстрактных областях, казавшихся вне приложений, и физиков-инженеров, и прежде всего радиотехников.
Основное внимание уделяется множествам, матрицам, графам, логике и вероятностям. Все эти разделы тесно связаны между собой, поэтому во вводной главе приведены краткие сведения по каждому из них, которые затем используются при более глубоком изложении материала. Внутренние ссылки даются тремя цифрами в скобках, означающими соответственно номера главы, параграфа, пункта. При ссылках на материал внутри главы ее номер опускается, а в пределах параграфа ссылка содержит только номер пункта.
При изучении вводной главы важно понять смысл основных определений, привыкнуть к соответствующей символике, научиться выполнять простейшие операции над математическими объектами. Этой цели должны способствовать приведенные в конце каждого параграфа задачи и упражнения, решение которых позволит закрепить и расширить изложенный материал. Даже если читатель отложит изучение специальных глав на будущее, то и тогда материал вводной главы может пригодиться при чтении специальной литературы и справочных пособий. Разумеется, каждый читатель в зависимости от его подготовки и целей наметит свой подход к использованию книги.
В конце каждой главы приведен краткий обзор литературы, который включает монографии и учебные пособия, использованные при подготовке той книги и рекомендуемые для более глубокого изучения затронутых в ней вопросов.
1. Математика в инженерном деле
1. Взаимодействие математики и техники. Технические науки развиваются в тесном взаимодействии и сотрудничестве с математикой. Это проявляется, с одной стороны, в использовании математического аппарата для решения научно-технических задач. С другой стороны, инженерная практика в значительной мере ориентирует и стимулирует развитие самой математики. Можно привести множество примеров, иллюстрирующих это положение.
Исследование различных типов дифференциальных уравнений с самого начала тесно связывалось с решением технических и физических проблем. Метод наименьших квадратов, ставший одним из эффективных средств обработки результатов наблюдений возник из потребностей геодезической практики. Начертательная геометрия развилась под влиянием строительного дела, архитектуры и механики. Огромный арсенал численных методов сформировался и продолжает развиваться благодаря практическим потребностям.
Взаимодействие математических и прикладных дисциплин приводит к их взаимному обогащению, причем этот процесс носит двусторонний характер. Нередко идеи и методы, разработанные для решения частных задач в какой-либо конкретной области, приобретают в процессе развития столь общее значение, что их строгое обоснование становится делом математиков. Те идеи и методы, которые выдерживаются всесторонние и подчас весьма длительные испытания, развиваются в математические теории, обслуживая затем более широкий класс задач, чем те, из которых они возникли.
Характерным примером в этом отношении является теория вероятностей, для оформления которой как раздела математики понадобилось несколько столетий, считая от первых попыток найти закономерности в азартных играх. Операционное исчисление, разработанное на интуитивном уровне в конце прошлого века для расчета электрических цепей, испытало на себе все превратности судьбы, но затем получило строгое обоснование и нашло свое место в теории интегральных преобразований.
Можно привести много других примеров, когда математические теории, возникающие и развивающиеся из внутренних потребностей математики, находят затем широкое практическое применение в других отраслях науки и техники. Так обстояло дело, например, с математической логикой, аппарат которой стал одним из основных средства проектирования автоматов и моделирования дискретных систем. Неэвклидовы геометрии, служившие первоначально целям аксиоматического обоснования математики, нашли применение при конструировании самолетов и ракет. Теория электромагнитных волн была разработана за несколько десятилетий до их обнаружения и практического использования.
В результате взаимодействия математики и техники возникают и успешно развиваются новые прикладные науки. Так, на стыке теории вероятностей с техникой связи и передачи сообщений возникла теория информации, методы которой используются не только в технике, но и в экономике, лингвистике, биологии. Под влиянием и при непосредственном участии математики развиваются такие общие науки как кибернетика, теория цепей и систем.
Одним из наиболее эффективных результатов взаимодействия математики и техники явилось создание современных вычислительных машин. Симбиоз математических методов и технических средств электроники, магнитной техники, прикладной оптики и механики уже весьма высоко зарекомендовал себя в этом отношении и открывает необозримые перспективы в будущем. Развитие вычислительной техники позволяет привести в действие более мощные ресурсы математики и усиливает ее роль как непосредственной производительной силы общества, способствуя тем самым прогрессу самой математики.
2. Современная математика. Наиболее характерной чертой современной математики является чрезвычайно высокая степень обобщения и абстракции. Традиционное определение математики как науки о пространственных формах и количественных отношениях уже не соответствует современному положению вещей, оно приобретает более глубокое и широкое содержание. Предмет современной математики составляют совокупности объектов самого общего вида и любые возможные отношения между ними.
Так, трехмерное геометрическое пространство обобщается на любое число измерений, и в этом многомерном пространстве изучаются пространственно подобные отношения (длина, расстояние, ортогональность). Алгебраические операции абстрагируются и распространяются на объекты любой природы, которые образуют различные структуры в зависимости от приписываемых им свойств (группа, кольцо, тело, поле). Под переменными понимаются не только обычные величины, но и функции, которые рассматриваются как объекты функциональных пространств. Изучаемые математикой объекты объединяют совокупности величин, для представления которых используются такие понятия как множества, матрицы, графы.
Что такое непустое множество
Предположим, что теорема доказана для натурального числа n, и докажем ее для числа n+1. Итак, пусть A
|1, n+1|, и f есть взаимно однозначное отображение A на B. Занумеровав элементы A соответствующими им числами, получим:
|1, n|. Мы получили противоречие с предположением индукции, чем наше утверждение, а значит, и вся теорема доказаны.
Из теоремы 1 легко следует
Теорема 2. Всякое непустое конечное множество равномощно одному и только одному отрезку натурального ряда.
По определению конечного множества непустое конечное множество A равномощно по крайней мере одному отрезку натурального ряда. Если бы оно было равномощно двум различным отрезкам 
, то по свойствам равномощности будет: |1, m|
|1, n|, что противоречит теореме 1, так как один из двух различных отрезков натурального ряда является собственным подмножеством другого.
Однозначно определенное для данного непустого конечного множества A натуральное число n такое, что A
|1, n|, называется числом элементов множества A. Числом элементов пустого множества называется число 0.
Из свойств равномощности следует, что два конечных множества тогда и только тогда равномощны, когда они имеют одно и то же число элементов. Поэтому число элементов можно принять за определение мощности конечного множества.
непустое множество
Смотреть что такое «непустое множество» в других словарях:
Непустое множество — Пустым множеством в математике называется множество, не содержащее ни одного элемента. В одних теориях множеств существование [по меньшей мере одного] пустого множества провозглашается (см. аксиому пустого множества), в других доказывается. Во… … Википедия
Множество — У этого термина существуют и другие значения, см. Множество (значения). Запрос «Целое» перенаправляется сюда; о типе данных в программировании см. Целое (тип данных). Множество одно из ключевых понятий математики, в частности, теории… … Википедия
ЧАСТИЧНО УПОРЯДОЧЕННОЕ МНОЖЕСТВО — непустое множество, на к ром зафиксирован нек рый порядок. Ч. у. м. является примером модели. Примеры Ч. у. м.: 1) множество натуральных чисел с обычным порядком; 2) множество натуральных чисел, где означает, что аделит b; 3) множество всех… … Математическая энциклопедия
Направленное множество — В математике, направленным множеством называется непустое множество A с заданным на нем рефлексивным транзитивным отношением ≤ (т. е. предпорядком), обладающее дополнительным свойством: для любых двух элементов из A найдется элемент из A… … Википедия
ПРОЕКТИВНОЕ МНОЖЕСТВО — множество, к рое может быть получено из борелевских множеств повторным применением операций проектирования и перехода к дополнению. П. м. классифицируются по классам, образующим проективную иерархию. Пусть I=ww бэровское пространство… … Математическая энциклопедия
Частично упорядоченное множество — У этого термина существуют и другие значения, см. Упорядоченное множество. Подмножества
Нечёткое множество — Эту страницу предлагается объединить с Теория нечётких множеств … Википедия
Нечеткое множество — Нечёткое (или размытое, расплывчатое, туманное, пушистое) множество понятие, введённое Лотфи Заде в 1965 г. в статье «Fuzzy Sets» (нечёткие множества) в журнале Information and Control [1]. Л. Заде расширил классическое канторовское понятие… … Википедия
Пушистое множество — Нечёткое (или размытое, расплывчатое, туманное, пушистое) множество понятие, введённое Лотфи Заде в 1965 г. в статье «Fuzzy Sets» (нечёткие множества) в журнале Information and Control [1]. Л. Заде расширил классическое канторовское понятие… … Википедия