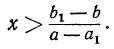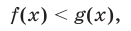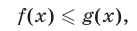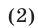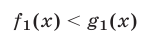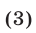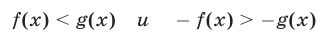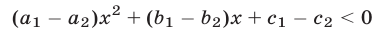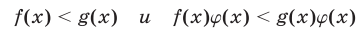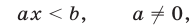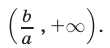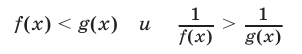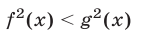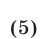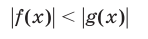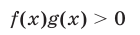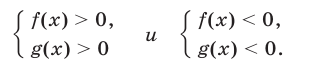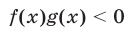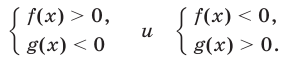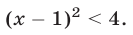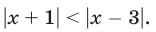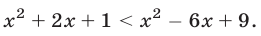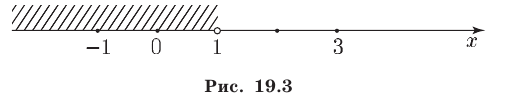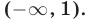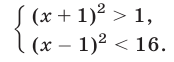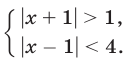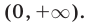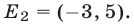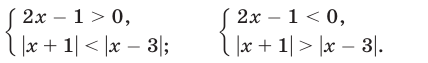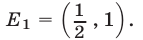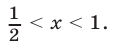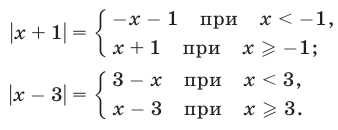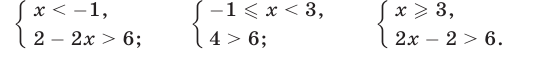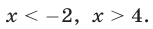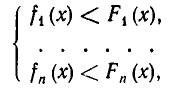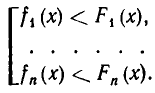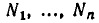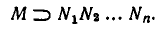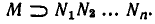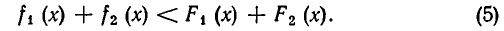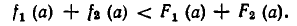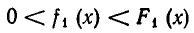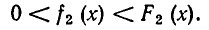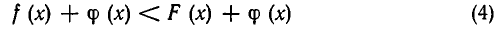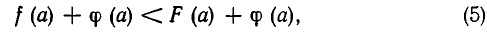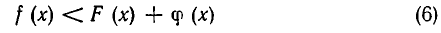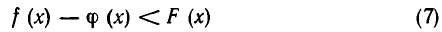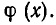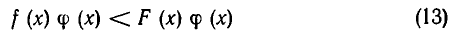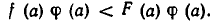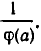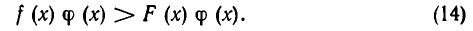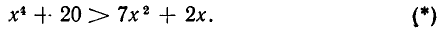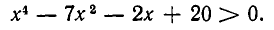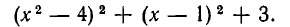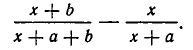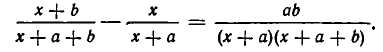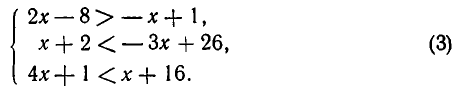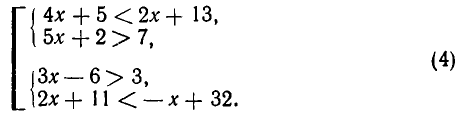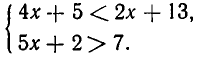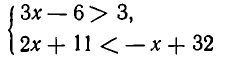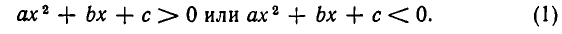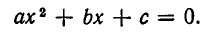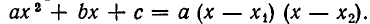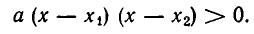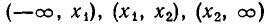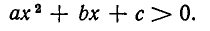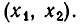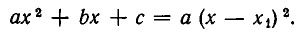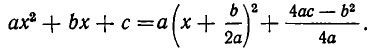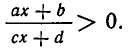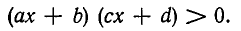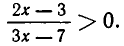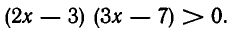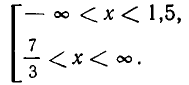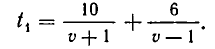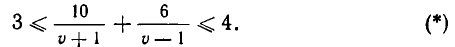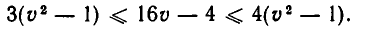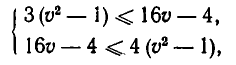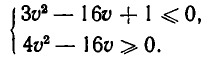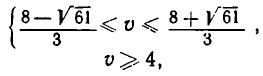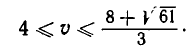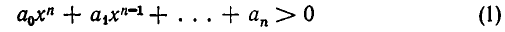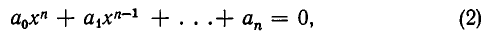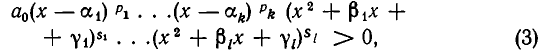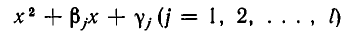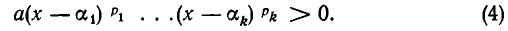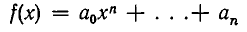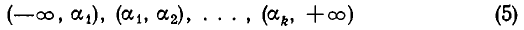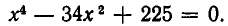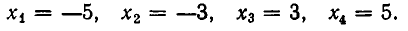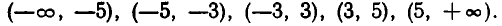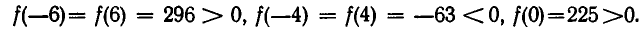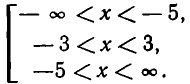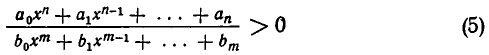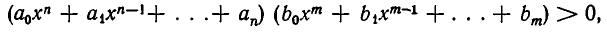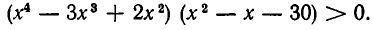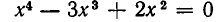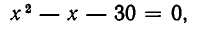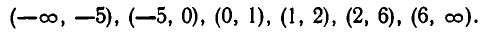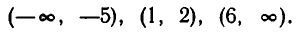Что такое неравенство первой степени
Решение неравенств первой и второй степени с одной переменной
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Решение неравенств первой и второй степени с одной переменной
Неравенства первой степени – это неравенства вида ах + b > 0 или ах + b ≥ 0, ах + b 0; 0,3x +1,2 > 0; 5 – 10x ≤ 0 являются неравенствами первой степени. Решим, например, последнее из этих неравенств: 5 – 10x ≤ 0 x ≥ 0,5 можно считать ответом, так как оно вполне ясно описывает множество всех значений x, являющихся его решениями. Можно также записать решение неравенства в виде числового промежутка: [0,5; +оо). Множеством решений неравенства первой степени всегда является числовой луч
Пример 1. Определим, в каком случае на координатной прямой изображено множество решений неравенства 19 – 7x > 20 – 3(x – 5).
2. Определить количество корней уравнения ах²+вх+с=0 и знак коэффициента а, если график квадратичной функции у = ах²+вх+с расположен следующим образом: у х у х у х у х 0 0 0 0 а) в) б) г)
3. Укажите промежутки, в которых функция у = ах²+вх+с принимает положительные и отрицательные значения, если её график расположен указанным образом: у у у х х х 0 0 0 х1 х2 х0 х0 а) б) в)
Определение. Неравенствами второй степени с одной переменной называют неравенства вида ах2+вх+с>0 и ах2+вх+с 0 2х2-7х 0
Рассмотреть функцию, соответствующую данному неравенству, определить направление ветвей параболы. Найти нули функции, т.е. абсциссы точек пересечения параболы с осью х, если они есть. Изобразить схематически параболу в координатной плоскости. Выбрать нужные промежутки. Записать ответ.
Решите неравенство: Вариант 1 Вариант 2 а) х²-9>0; а) х²-16 0; в) –х²-10х-25>0. в) –х²+6х-9>0.
Правильные ответы: Вариант 1 Вариант 2 а) (-∞;-3)U(3;+∞); а) (-4;4); б) (3;5); б) (-∞;3)U(7;+∞); в) решений нет. в) решений нет.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-1408428
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
В Оренбурге школьников переведут на дистанционное обучение с 9 декабря
Время чтения: 1 минута
ВПР для школьников в 2022 году пройдут весной
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Утверждено стратегическое направление цифровой трансформации образования
Время чтения: 2 минуты
Псковских школьников отправили на дистанционку до 10 декабря
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Рациональные неравенства. Метод интервалов
Понятие рациональных неравенств с одной переменной и их решения
Общие свойства неравенств и линейные неравенства с одной переменной подробно рассматриваются в Главе 6, §§36-40 справочника для 8 класса.
Каждая из сторон рационального неравенства с одной переменной является рациональным выражением с этой переменной.
Решением рационального неравенства с одной переменной называют такое множество всех значений этой переменной, при подстановке которых в это неравенство вместо неизвестного получается верное числовое неравенство.
При решении неравенств используются свойства неравенств (см. §36 справочника для 8 класса), из которых следует:
Алгоритм решения неравенств первой степени
Напомним, что неравенство первой степени также называют «линейным неравенством» (см. Главу 6, §§36-40 справочника для 8 класса)
Алгоритм решения неравенств второй степени
$a = 1 \gt 0$, парабола ветками вверх, точки над осью OX соответствуют
$x \in (-\infty;-5) \cup (-2;+\infty)$
Метод интервалов
Заметим, что при x = a, f(x) = 0.
Введём понятие «белой» (незакрашенной) и «чёрной» (закрашенной) точек.
Cформулируем следующее правило:
Получим такое соответствие схем и решений:
$x-a \lt 0, x \in (-\infty;a)$
$x-a \le 0, x \in (-\infty;a]$
$x-a \ge 0, x \in [a;+\infty)$
Теперь понятен смысл «белых» и «чёрных» точек.
«Белые» точки не входят в множество решений.
«Чёрные» точки входят в множество решений.
Исследуем знаки для функции f(x) = (x-a)(x-b). Это – парабола, ветками вверх, и для неё, как было показано выше:
В качестве примера, для строгих и нестрогих неравенств получаем:
$x \in (- \infty ;a) \cup (b;+ \infty )$
$ x \in (- \infty ;a] \cup [b;+ \infty )$
Посмотрим, как это работает на практике.
Вся числовая прямая теперь разделена на три области:
Помечаем всю третью область знаком «+».
Преимущества метода интервалов:
Обобщение метода интервалов для целых рациональных неравенств любой степени
В общем случае в целом рациональном неравенстве слева стоит многочлен степени n:
СЛУЧАЙ 1. Линейные сомножители в 1-й степени
Шаг 2. Из каждой области выбрать произвольный x, подставить в выражение слева, определить его знак, пометить область «+» или «-».
Шаг 3. Выбрать области, помеченные «+». Записать ответ как объединение этих промежутков.
Для нестрогих неравенств действуем также, только точки на прямой должны быть «чёрными» и включаться в множество решений (с помощью квадратных скобок).
Отмечаем на прямой корни (т.е. такие x, которые обращают каждую из скобок в 0).
Неравенство строгое – все точки на числовой прямой «белые»:
Числовая прямая делится на 4 области:
Из каждой области выбираем произвольный x, подставляем в (x-4)(x+3)(x-1), и находим знак произведения скобок:
Заменяем третью скобку с кубом (нечетная степень) на скобку в первой степени:
Решаем полученное неравенство с линейными сомножителями в 1-й степени.
Неравенство строгое – все точки на числовой прямой «белые»:
Убираем первую скобку с квадратом (чётная степень), записываем корень из этой скобки в совокупность:
Заменяем третью скобку с кубом (нечетная степень) на скобку в первой степени:
Решаем полученное неравенство с линейными сомножителями в 1-й степени.
Неравенство нестрогое – все точки на числовой прямой «чёрные»:
Поэтому, при решении неравенств, такие скобки просто убираются, т.к. на знак выражения они не влияют.
$x-1 \lt 0 \Rightarrow x \lt 1$
Примеры
Пример 1. Решите неравенства:
$ D = 121-4 \cdot 2 \cdot (-6) = 169 = 13^2$
Пример 2. Найдите наименьшее целое число, удовлетворяющее неравенству:
Наименьшее целое x = 2
$3x^2-5x-2-2(x^2-2x+1)+3 \lt 0$
Наименьшее целое x = 0
Пример 3. Решите неравенство:
$ x^2+4 \ge 4 \gt 0$, на знак не влияет, сокращаем
Неравенство строгое. Убираем первую скобку с чётной степенью, добавляем требование неравенства корню в систему. Заменяем скобку с нечётной степенью на скобку в 1-й степени:
$ г) (x+4)^3 (x-2)^4 (x+6)^5 \le 0$
Неравенство нестрогое. Убираем вторую скобку с чётной степенью, добавляем требование равенства корню в совокупность. Заменяем скобку с нечётной степенью на скобку в 1-й степени:
$ \left[ \begin
Решение линейных неравенств
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.
Линейные неравенства — это неравенства вида:
где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит сделать так, чтобы в левой части осталось только неизвестное в первой степени с коэффициентом равном единице.
Типы неравенств
Линейные неравенства: свойства и правила
Вспомним свойства числовых неравенств:
Если же а b и c > d, то а + c > b + d.
Если а 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
Если а d, то а – c b, m — положительное число, то mа > mb и
Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).
Если же а > b, n — отрицательное число, то nа
Обе части можно умножить или разделить на одно отрицательное число, при этом знак поменять на противоположный.
Если а 0, то аc b, где а, b > 0, то а2 > b2, и если а b, где а, b > 0, то
b» height=»45″ src=»https://lh5.googleusercontent.com/MuRDPQeqxIZvVG_mHVaktFp6nlIEEbz8zdRs1ZW8CZbZacJrS4aKzrDyhKxXpJvc35TSAgiRpqr-63sGzL9_sPU80vFhR0ZDAmSmRFZtwEldDkWRttfSGuaJJIb7xWxZDugU3xTt»>
Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.
Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.
Свойства выше помогут нам использовать следующие правила.
Правила линейных неравенств
Решение линейных неравенств
Со школьных уроков мы помним, что у неравенств нет ярко выраженных различий, поэтому рассмотрим несколько определений.
Неравенства ax + b > 0 и ax > c равносильные, так как получены переносом слагаемого из одной части в другую.
Определение 3. Линейные неравенства с одной переменной x выглядят так:
где a и b — действительные числа. А на месте x может быть обычное число.
Равносильные преобразования
Рассмотрим пример: 0 * x + 5 > 0.
Как решаем:
Метод интервалов
Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.
Метод интервалов это:
Если a ≠ 0, тогда решением будет единственный корень — х₀;
Для этого найдем значения функции в точках на промежутке;
Как решаем:
Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.
Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.
По чертежу делаем вывод, что решение имеет вид (−∞, 4) или x
Графический способ
Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.
Алгоритм решения y = ax + b графическим способом
Рассмотрим пример: −5 * x − √3 > 0.
Как решаем
Ответ: (−∞, −√3 : 5) или x
Алгебраические неравенства с примерами решения
Неравенство в математике — это отношение, связывающее два числа или иных математических объекта с помощью одного из перечисленных ниже знаков.
Неравенства первой степени
Мы уже говорили, в каком смысле надо понимать выражение „больше“ и „меньше“ применительно к относительным числам, а именно: выражение „а больше b“ (а>b) означает, что разность а — b есть число положительное, а выражение „а меньше b“ (α или b, то b —3; — 3 b и b > с, то а > с; например: — 2 > —Зи—3 > —4; тогда—2 > —4.
Если обе части неравенства умножим или разделим на одно и то же положительное число, то знак неравенства не изменится.
Например, умножив на +4 части неравенства —5 > —7, получим: —20 >—28.
7) Если a > b и m — отрицательное число, то am —7, получим: 5 Равносильные неравенства
Неравенства, содержащие одни и те же неизвестные, называются равносильными, если они удовлетворяются одними и теми же значениями этих неизвестных; так, два неравенства 3x+3 B (1)
и
А+m > B + m (2)
равносильны. Положим, что первое неравенство удовлетворяется при некоторых значениях букв. Это значит, что при этих значениях численная величина А больше численной величины В; но тогда, на основании свойства 3, при тех же значениях букв и численная величина суммы A+m больше численной величины суммы B+m, так как если к обеим частям неравенства прибавим поровну, то знак неравенства не изменится. Значит, всякое решение неравенства (1) удовлетворяет и неравенству (2).
Обратно, если при некоторых значениях букв численная величина суммы A+m больше численной величины суммы B+m, то для тех же значений букв и численная величина А больше численной величины В (неравенство не нарушится, если к обеим частям неравенства прибавим— m следовательно, все решения неравенства (2) удовлетворяют и неравенству (1); значит, эти неравенства равносильны.
Так как вычитание равносильно сложению с противоположным числом, то, следовательно, от обеих частей неравенства можно отнять одно и то же число.
Следствие. Любой член неравенства можно перенести из одной части в другую с противоположным знаком.
Если, например, имеем неравенство A > B + C, то, прибавив к обеим частям по—С, получим: А—С > В.
Теорема:
Если обе части неравенства (содержащего неизвестные) умножим (или разделим) на одно и то же положительное число, то получим новое неравенство, равносильное первому.
Докажем, что два неравенства:
A>B (1)
и
Аm > Bm (2)
равносильны, если только m—положительное число.
Обратно, если при некоторых значениях букв численная величина Am больше численной величины Вm, то при тех же значениях букв и численная величина А больше численной величины В, так как от деления обеих частей неравенства на положительное число знак неравенства не изменяется.
Замечание:
Множитель, (х—5)² остаётся положительным числом при всех значениях х, кроме одного: х=5. Значит, неравенства (1) и (2) равносильны в том случае, если первое из них не удовлетворяется значением х=5; в противном же случае неравенство (1), удовлетворяясь всеми решениями неравенства (2), имеет ещё решение: х = 5 (это решение неравенству (2) не удовлетворяет, ибо при х = 5 неравенство (2) обращается в равенство).
Следствие. Если обе части неравенства содержат положительный общий множитель, то на него можно разделить обе части неравенства.
Теорема:
Если обе части неравенства (содержащего неизвестные) умножим (или разделим) на одно и то же отрицательное число и при этом переменим знак неравенства на противоположный, то получим новее неравенство, равносильное первому.
Эта теорема доказывается совершенно так же, как и теорема 2; надо только принять во внимание, что от умножения или деления обеих частей неравенства на отрицательное число знак неравенства изменяется на противоположный.
По поводу этой теоремы можно высказать такое же замечание, какое было сделано по отношению к теореме 2.
Следствия. а) Переменив у всех членов неравенства знаки на противоположные (т. е. умножив обе его части на —1), мы должны изменить знак неравенства на противоположный.
б) Нельзя умножить обе части неравенства на буквенный множитель, знак которого неизвестен.
в) Неравенство с дробными членами можно привести к целому виду. Возьмём, например, такое неравенство:
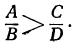
Перенесём все члены в левую часть и приведём их к общему знаменателю:
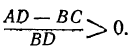
Если BD — положительное число, то мы можем его отбросить, не изменяя знака неравенства, потому что отбросить BD — всё равно, что умножить на это число обе части неравенства. Отбросив BD, получим неравенство, не содержащее дробей:
AD — BС > 0.
Если BD — отрицательное число, то мы можем его отбросить, переменив при этом знак неравенства на противоположный; тогда снова будем иметь неравенство с целыми членами:
AD — BC Доказательство неравенства
Нельзя установить каких-либо общих правил для обнаружения верности предложенного неравенства. Заметим только, что один из приёмов состоит в том, что предложенное неравенство преобразовывают в другое — очевидное, и затем, исходя из этого очевидного неравенства, путём логических рассуждений доходят до предложенного. Приведём пример:
Доказать, что если сумма чисел х и у постоянна, то их произведение будет наибольшее, если х=у.
Пусть х+у = а, где а—постоянное число. Если х=у, то каждое из этих чисел будет 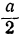
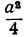
Требуется доказать, что если х ≠ у, то 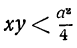
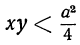
Общий вид неравенства первой степени с одним неизвестным, после раскрытия в нём скобок и освобождения от дробных членов, следующий:
ax + b> a₁x + b₁.
Если а — a₁ > 0, то, разделив на а — a ₁ обе части неравенства, найдём:
Пример:
Решить неравенство: 2x(2x — 5) — 27 — 2.
4x+ 1. Переносим члены и делаем приведение: — 14x — 2.
Два неравенства первой степени с одним неизвестным
Рассмотрим систему двух неравенств:
ax+b> a’x +b’ и cx+d> c’x + d’.
Каждое из этих неравенств даёт по одному пределу для неизвестного.
При этом могут представиться три случая:
Пример:
Решить два неравенства: 0,3x + 5 25, второе: x Основные понятия, связанные с решением неравенств
Опыт проведения приемных экзаменов в вузы свидетельствует о том, что многие абитуриенты допускают ошибки при решении неравенств.
Если при решении уравнений можно использовать преобразования, приводящие к появлению посторонних корней, которые выявляются с помощью проверки, то при решении неравенств обычно нет возможности отсеять посторонние решения, так как множество решений неравенства, как правило, бесконечно.
Поэтому при решении неравенства нужно внимательно следить за тем, чтобы в процессе решения не менялось множество его решений, т. е. чтобы при каждом преобразовании неравенство заменялось равносильным.
Рассмотрим основные понятия, связанные с решением неравенств. Если на некотором множестве Е определены функции f(x) и g(x) и ставится задача решить неравенство
то это означает, что требуется найти все значения 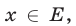
Каждое такое значение х называется решением неравенства, а совокупность всех решений — множеством решений этого неравенства.
Из этого определения следует, что каждое решение неравенства (1) принадлежит множеству, которое является пересечением (общей частью) областей определения функций f(x) и g(x) и называется областью допустимых значений (ОДЗ) неравенства (1).
Неравенство вида (1) называют строгим в отличие от неравенства
которое называют нестрогим.
Множество решений неравенства (2) можно получить, объединив множество решений неравенства (1) с множеством решений уравнения f(x) = g(x).
При решении неравенств, как и при решении уравнений, широко используется понятие равносильности.
Неравенство (1) и неравенство
называют равносильными на множестве М, если множества решений этих неравенств совпадают, т. е. каждое решение неравенства (1), принадлежащее множеству М, является решением неравенства (3) и, обратно, каждое решение неравенства (3), принадлежащее множеству М, является решением неравенства (1). Если неравенства (1) и (3) не имеют решений, то эти неравенства считаются равносильны-
Сформулируем основные утверждения, связанные с понятием равносильности.
равносильны на любом числовом множестве.
2°. Если функции f(x), g(x) и h(x) определены на множестве М, то неравенства
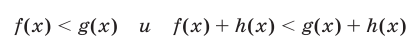
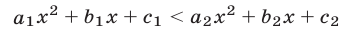
при любых 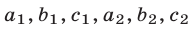
на множестве R.
3°. Если функции 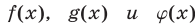
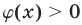
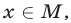
равносильны на множестве М.
Применяя утверждения 1° и 3° к линейным неравенствам, т. е. к неравенствам вида
а) если 
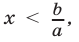
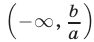
б) если 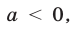
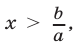
4°. Если 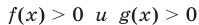
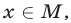
равносильны на множестве М.
5°. Если функции f(x) и g(x) определены на множестве М, то неравенство
В случае, когда f(x) > 0 и g(x) > 0 для всех 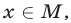
равносильно совокупности следующих двух систем неравенств:
равносильно совокупности следующих двух систем неравенств:
Примеры с решениями:
Пример:
Решить неравенство
Решение:
Это неравенство равносильно следующему: 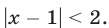
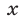
Пример:
Решить неравенство
Решение:
Первый способ. Так как обе части неравенства неотрицательны, то при возведении их в квадрат получается равносильное неравенство
Это неравенство равносильно неравенству 8х
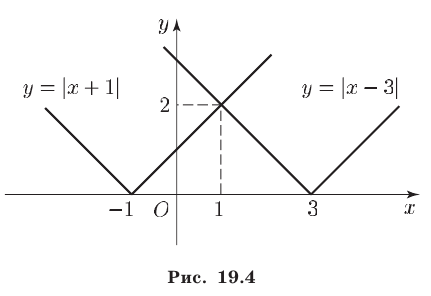
Третий способ. Построим графики функций 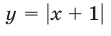
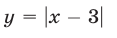
Эти графики пересекаются в точке (1;2). При х 1 — выше. Поэтому множество решений данного неравенства — промежуток
Пример:
Решить систему неравенств
Решение:
Данная система равносильна следующей:
Множество 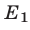
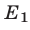
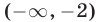
Множество 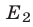
Множество Е решений исходной системы — общая часть (пересечение) множеств 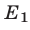
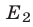
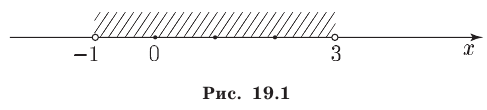
Следовательно, множество Е — объединение интервалов (-3,-2) и (0,5).
Ответ. —3
Множество 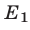
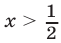
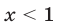
Множество 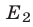
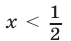
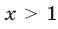
Ответ.
Пример:
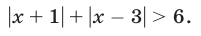
Решение:
Первый способ. Используя определение модуля, получаем
Пусть 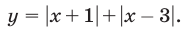
Поэтому неравенство (8) равносильно совокупности следующих систем неравенств:
Множество 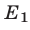
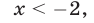
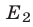
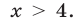
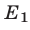
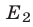
Ответ.
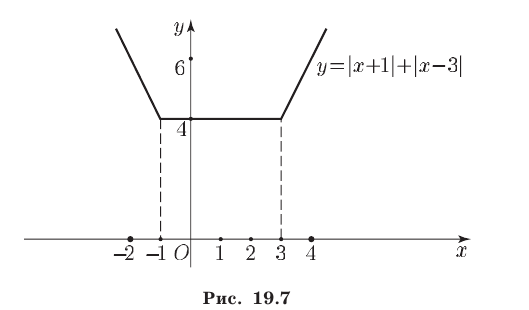
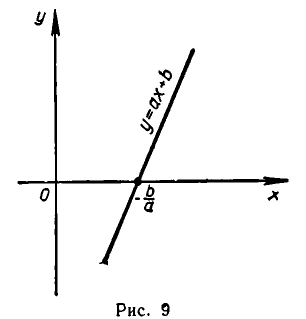
Второй способ. Решить неравенство (8) — значит найти все точки х числовой прямой, сумма расстояний от каждой из которых до точек —1 и 3 больше 6 (рис. 19.6).
Найдем точку 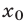
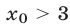
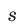
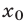
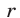
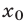
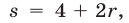
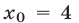
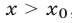
При х 4 график расположен выше прямой у = 6. Поэтому решениями неравенства (8) являются все х такие, что х 4.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
Функциональные неравенства
Перейдем к изучению неравенств между функциями от одного или нескольких переменных. Задачи о таких неравенствах распадаются на два больших класса. В одних задачах требуется доказать, что в той или иной области, где заданы две функции, их значения удовлетворяют заданному неравенству. Мы будем говорить в этом случае, что неравенство выполняется в этой области тождественно. Такие задачи называют задачами на доказательство не равенств.
Иной вид имеют задачи второго типа. Здесь задано неравенство между функциями и надо найти все значения аргумента (или аргументов, если функции зависят от нескольких переменных), для которых это неравенство выполняется. Такие задачи мы будем называть задачами на решение неравенств.
Теория неравенств во многом напоминает теорию уравнений. Существенным отличием является то, что уравнение, как правило, имеет конечное множество решений. Решения же неравенств с одним неизвестным заполняют целые промежутки на числовой оси. Для неравенств со многими неизвестными мы получаем в качестве решений области на плоскости, в пространстве и т. д.
Понятия системы неравенств и совокупности неравенств определяются точно так же, как и для уравнений. Именно, мы будем говорить, что задана система неравенств
если надо найти все значения х, при которых выполняются в с е эти неравенства. Если же надо найти все значения х, при которых выполняется хоть одно из неравенств 
Рассмотрим сначала некоторые общие вопросы теории функциональных неравенств.
Следствия из неравенств
Пусть дана система неравенств
Мы будем говорить, что неравенство
является следствием системы неравенств (1), если оно имеет место для любого х, удовлетворяющего всем неравенствам (1). Иными словами, если выполняются все неравенства (1), то должно выполняться и их следствие (2 ).
Это определение можно сформулировать следующим образом. Обозначим через 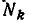
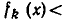
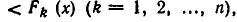
В самом деле, пересечение множеств 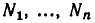
Чаще всего приходится пользоваться следующими утверждения ми о следствиях из неравенств.
Теорема:
Если на некотором множестве А выполняются неравенства
то на А имеет место и неравенство
Доказательство. Пусть а — число из множества А. Тогда справедливы числовые неравенства
Следовательно, имеет место неравенство:
Оно показывает, что при 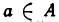
Точно так же доказывается следующая
Теорема:
Пусть на некотором множестве А выполняются неравенства
Тогда на этом множестве имеет место и неравенство
Равносильные неравенства
Введем следующее определение.
Определение:
называются равносильными, если каждое число, удовлетворяющее неравенству (1), удовлетворяет и неравенству (2), а каждое число, удовлетворяющее (2), удовлетворяет и (1) (в частности, если множества решений обоих неравенств пусты).
Иными словами, два неравенства равносильны, если каждое из них является следствием другого.
Для установления равносильности двух неравенств применяются следующие теоремы.
Теорема:
Пусть функция 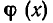
Для доказательства этой теоремы достаточно заметить, что из f (а)
а из (5) следует f(а)
В самом деле, (6) получается из (7) прибавлением к обеим частям функции —
Точно так же доказывается следующая
Теорема:
равносильны. Равносильны и неравенства
Наконец, докажем следующую теорему.
Теорема:
Пусть функция ср (х) определена при всех допустимых значениях х и положительна. Тогда неравенства
Доказательство. Пусть а — число, удовлетворяющее неравенству (12): f(а)
Это показывает, что а удовлетворяет неравенству (13), а потому (13) является следствием (12). Точно так же доказывается, что (12) является следствием (13). Для этого достаточно умножить обе части неравенства (13) на положительное число
Если же функция ф (а) определена для всех допустимых значений х и отрицательна, то неравенство f(x)
Мы доказывали теоремы о равносильности для неравенства с одним переменным. Эти теоремы остаются верными и для неравенств с несколькими переменными.
Доказательство неравенств
Для доказательства неравенств применяют один из следующих двух путей.
1) Исходят из неравенства, которое надо доказать, и последовательно заменяют его равносильными неравенствами, пока не дойдут до очевидного неравенства. Так как на каждом шагу получалось неравенство, равносильное данному, то тем самым справедливость данного неравенства доказана.
2) Исходят из какого-нибудь очевидного неравенства и заменяют его неравенствами-следствиями до тех пор, пока не придут к доказываемому неравенству. Мы знаем, что неравенство 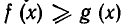
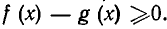
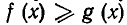
Рассмотрим следующий пример. Доказать неравенство
Это неравенство равносильно неравенству
Перепишем левую часть в виде
Так как, очевидно 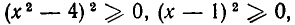
Далее докажем, что дробь 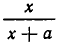
Для этого составим разность левой и правой частей неравенства:
Приведя дробит к одному знаменателю, получаем:
Так как правая часть этого равенства заведомо положительна, то неравенство (**) доказано.
Теперь приведем пример на использование второго способа доказательства неравенства. Докажем, что для любого действительного числа х имеет место неравенство
Будем исходить из очевидного неравенства
Раскроем скобки в выражении (2). Мы получим неравенство 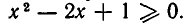
Линейные неравенства
Перейдем теперь к методам решения неравенств. Начнем с простейшего случая — линейного неравенства с одним неизвестным. Такое неравенство имеет вид ах+ b > 0 или ах+b 0. В случае, когда b — положительное число, это неравенство справедливо для всех значений х, а в случае, когда b — отрицательное число, оно не имеет места ни при одном значении х.
Рассмотрим более интересный случай, когда 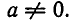
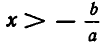
Итак, неравенство ах +b >0, где а — положительное число, равносильно неравенству 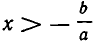
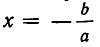
Ясно, что слева от точки — 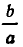
К неравенствам рассмотренного вида сводится решение более общих неравенств
В самом деле, неравенство (1) равносильно
К решению линейных неравенств сводится решение систем и совокупностей линейных неравенств. Чтобы найти решение систем линейных неравенств, надо решить каждое из них, а потом взять пересечение получившихся множеств. При решении совокупности линейных неравенств надо решить каждое из них и взять сумму получившихся множеств.
Пример:
Решить систему неравенств:
Решением первого из них является x > 3, второго х
Сначала решим систему неравенств:
Так же, как и в примере 1, получаем промежуток 1
является промежуток 3 Решение неравенств второй степени
Перейдем теперь к решению квадратных неравенств, то есть неравенств вида
Мы можем, не теряя общности, считать, что а > 0.
Мы покажем сейчас, что решение неравенств второй степени сводится по сути дела к решению квадратных уравнений. При этом возможны различные случаи, в зависимости от знака дискриминанта 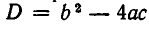
а) Пусть D > 0. В этом случае, как мы знаем, квадратное уравнение (2) имеет два различных действительных корня 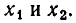

Значит, неравенство 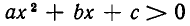
Сомножитель 


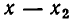
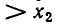

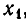
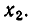
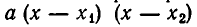
Иными словами, на каждом из промежутков
квадратный трехчлен 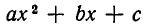
Итак, мы доказали следующее утверждение: если квадратный трехчлен 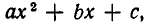
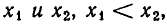
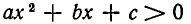
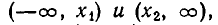
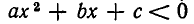
б) Пусть D = 0. В этом случае квадратный трехчлен 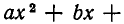
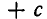
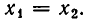
Но 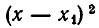
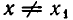
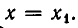
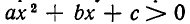
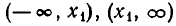
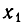
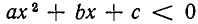
в) Наконец, рассмотрим случай, когда D
По условию имеем 
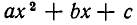
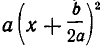
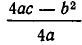
Итак, если D 0, то неравенство 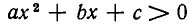
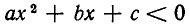
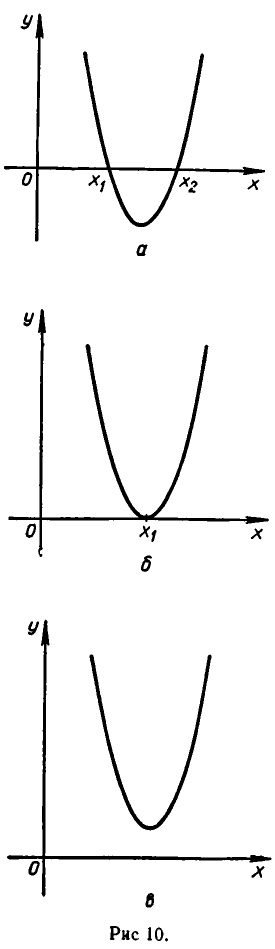
Полученные результаты допуска ют простое геометрическое истолкование. Рассмотрим функцию 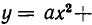
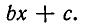
Если В > 0, то эта парабола пересекает ось в двух точках 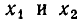
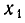
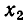
Если D = 0, то парабола касается оси Ох в некоторой точке 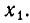
Наконец, при D 0 парабола не пересекает оси Ох и расположена выше нее. Поэтому для всех значений х выполняется неравенство 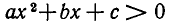
К неравенствам второй степени сводятся неравенства вида
Умножив обе части неравенства на 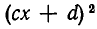
Пример:
Это неравенство равносильно неравенству
Корнями функции (2х — 3) (Зх — 7) являются числа 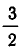
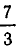
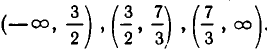
Приведем пример задачи, сводящейся к решению квадратных неравенств.
Задача:
Лодка спускается по течению реки на расстояние 10 км, а затем поднимается против течения на расстояние 6 км. Скорость течения реки равна 1 км/ч. В каких пределах должна лежать собственная скорость лодки, чтобы вся поездка заняла от 3 до 4 часов?
Решение. Пусть v — собственная скорость лодки. Тогда ее скорость по течению реки равна v + 1, а против течения реки равна v — 1. Поэтому время движения лодки равно
Итак, мы получили систему неравенств
то есть систему неравенств
Корнями_ уравнения 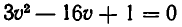
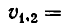
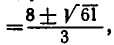
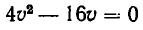
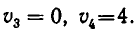
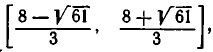
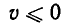
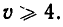
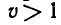
из которой окончательно получаем:
Решение алгебраических неравенств высших степеней
Мы видели, что решение квадратичного неравенства свелось по сути дела к решению квадратного уравнения. Корни 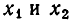
Точно так же решение неравенства вида
сводится к решению алгебраического уравнения
точнее говоря, к отысканию действительных корней этого уравнения. Чтобы осуществить это сведение, нам понадобится следующее утверждение, которое будет доказано в главе V (см. стр. 238): любой многочлен с действительными коэффициентами разлагается на множители первой и второй степеней, причем множители второй степени не имеют действительных корней.
Поэтому неравенство (1) можно записать так:
не имеют действительных корней и потому положительны на всей числовой оси (см. п. 2). Поэтому, отбрасывая эти множители, мы приходим к равносильному неравенству
А теперь заметим, что множитель 
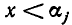
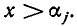

в порядке возрастания, то на промежутках
многочлен f(х) сохраняет постоянный знак. Поэтому достаточно выбрать на каждом из промежутков (5) «пробную точку» и найти знак многочлена f(х) в этой точке. Тот же знак многочлен будет иметь и на всем промежутке. Вместо подсчета значения в «пробной точке» можно подсчитать число положительных и отрицательных сомножителей в разложении (4).
Найдем сначала корни уравнения
Это биквадратное уравнение. Решая его, получаем корни:
Найденные корни разбивают действительную ось на промежутки
Отсюда вытекает, что решение неравенства (4) состоит из промежутков 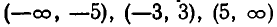
решаются точно так же. Именно, умножим числитель и знаменатель на один и тот же множитель 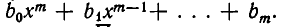
которое решается описанным выше образом.
Пример:
Это неравенство равносильно следующему:
находим их корни:
Расположим эти корни в порядке возрастания. Полученные числа разбивают действительную ось на промежутки:
Методом «пробных точек» находим, что решение неравенства (6) состоит из промежутков:
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института