Что такое незамкнутая ломаная
Ломаная линия — что это такое простыми словами
Ломаная линия — определение
Одним из наиболее простых и понятных геометрических терминов считают прямую линию. Есть в математике похожая фигура, но с некоторыми характерными чертами. Давайте попробуем разобраться, что такое ломаная линия и каковы её особенности.
Ломаная линия — математическая фигура, включающая в себя несколько отрезков, которые меняют направление.
Если выражаться более чётко, то это черта, которая не является прямой по всей длине, но может не иметь изгибов на отдельном отрезке.
Таким образом, фигура в обязательном порядке отвечает нескольким признакам:
Обозначение ломаной линии
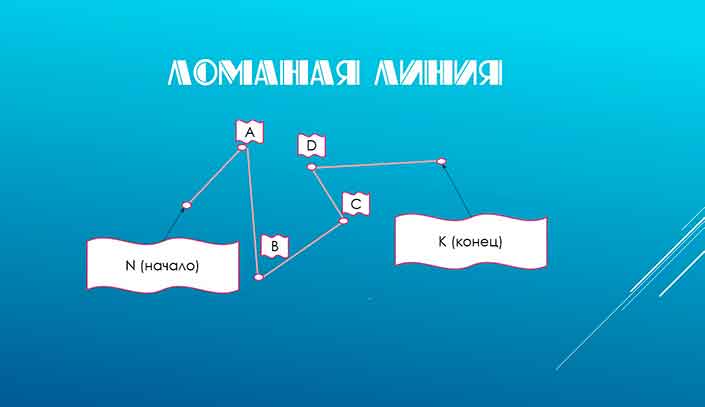
Чтобы отметить ломаную линию на чертеже вам необходимо указать наименования точек стыка, в которых она меняет направление, латинскими буквами.
Из чего состоит ломаная линия
Как вы уже успели заметить, на рисунках присутствуют звенья — отрезки, составляющие ломаную линию. А вот начальные и конечные точки этих составных частей — вершины. На картинке вершины ломаной ABCD — позиции A, B, C, D.
Признак замкнутости ломаной линии
Классификация ломаных линий прежде всего осуществляется по свойству замыкания.
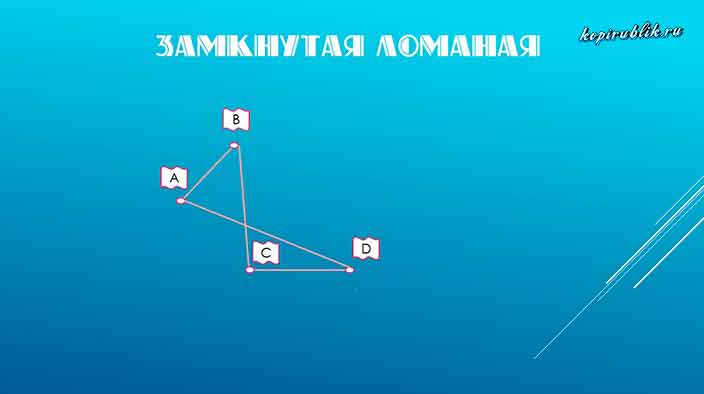
Замкнутая ломаная линия — фигура, у которой конечная позиция совпадает с начальной. Иначе говоря, когда она заканчивается в том же месте, где начиналась.
Яркие представители — треугольник и квадрат, а также остальные виды многоугольников:
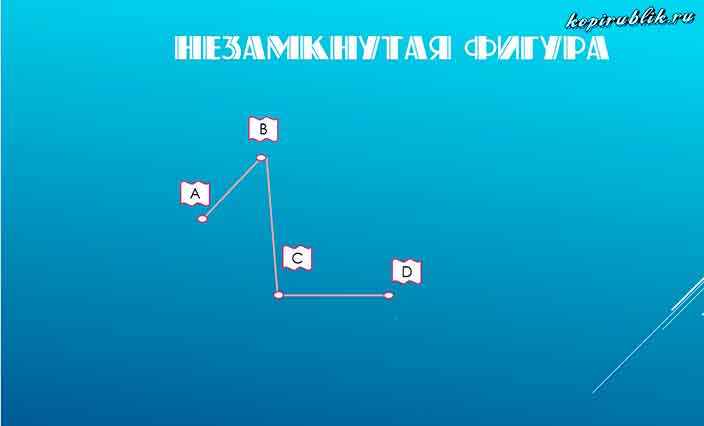
Незамкнутая ломаная линия — фигура, которая приходит в позицию, отличающуюся от начальной.
Время от времени, у учащихся возникает вопрос: «Как определить, замкнутая фигура или нет?». Ответ будет весьма прост:»Когда число отрезков равно количеству вершин — она замкнутая, а при наблюдающемся неравенстве — незамкнутая».
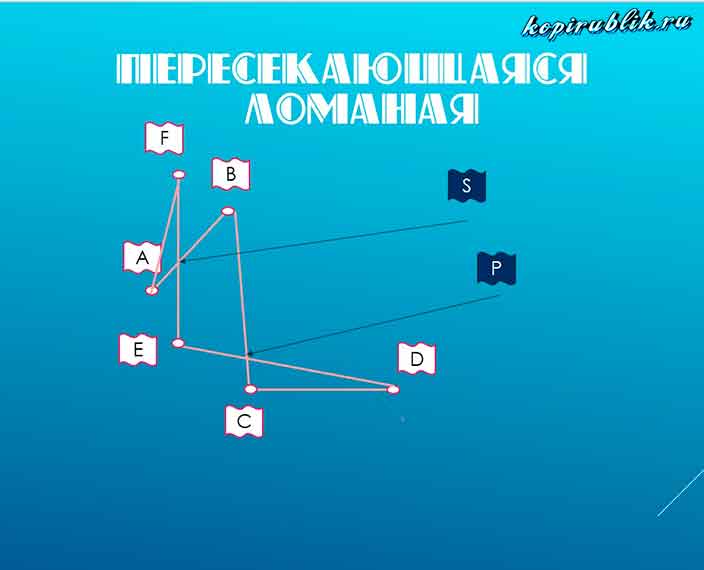
В качестве дополнительного вида рассматривают понятие самопересекающаяся ломаная линия — та, которая скрещивается на пути своего следования. Для данного термина не имеет значения сколько раз произошло пересечение.
На рисунке отмечены точки пересечения — S, P, а также вершины — A,B,C,D,E,F.
Иногда люди спрашивают — «Могут ли вершины являться точками пересечения?». Чтобы найти ответ, обратите внимание на рисунок с пересекающейся и одновременно замыкающейся — ломаной линией:
Изображение отличается от предыдущего: отрезок EB перемещён, поэтому вершина A приобрела статус точки пересечения.
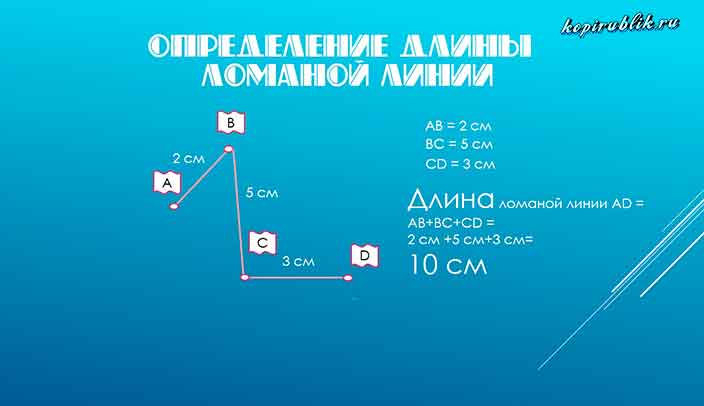
Как измерить длину ломаной линии
Ломаная линия, имеющая начало и конец, имеет распространённую стандартную характеристику — длину. Имея цель сделать замер её длины, необходимо суммировать длины всех её составных частей — отрезков.
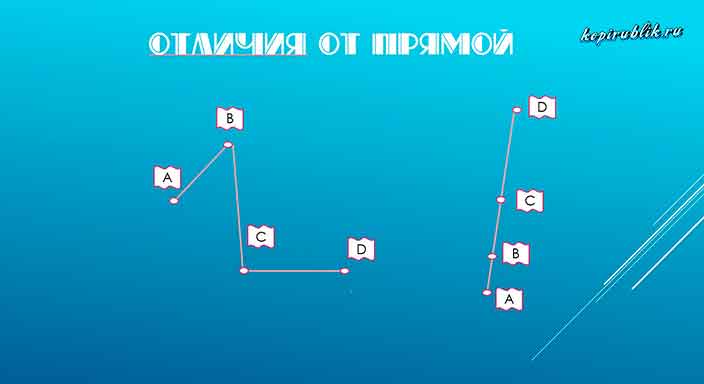
Чем ломаная линия отличается от прямой
При взгляде на рисунок очевидно: уникальный признак ломаной линии — отсутствие углов, равных 180 градусам. В остальном, фигуры одинаковые и обладают схожими свойствами, например, длиной.
Примеры ломаных линий в быту
В целях наилучшего усвоения теории, разумно на практике ознакомиться с примерами ломаных линий из жизни.
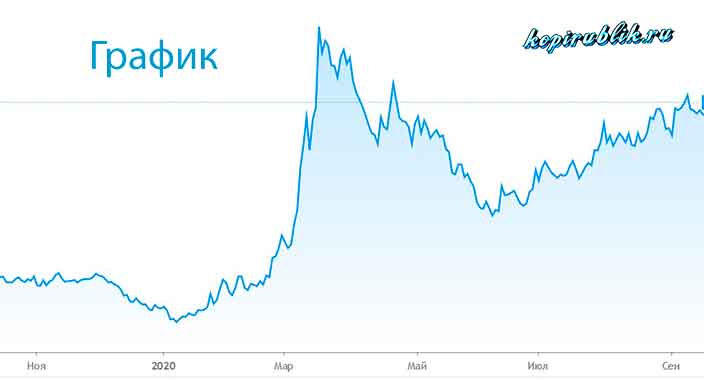
Ломаная линия— график фондового рынка. Так как отрезки графика очень маленькие, поэтому может показаться, что это кривая, но при ближайшем рассмотрении оказывается, что это не так.
Фасад дома при переводе на «язык геометрии» выглядит как замкнутая ломаная линия.
Пирамиды древнего Египта обладали формой треугольника — одной из самых популярных ломаных линий.
Урок математики в 1-м классе. Тема: «Ломаная линия»
Продолжительность урока: 35 минут
Тип урока: Изучение и первичное закрепление нового материала.
Цель: Познакомить с ломаной линией и ее компонентами.
Задачи урока:
Ведущий вид деятельности: продуктивный, творческий, проблемный
Методы работы: объяснительно-иллюстративные, частично-поисковые, словесные, наглядные, практические.
Функция учителя: организатор сотрудничества; консультант, управляющий поисковой работой.
Педагогические технологии:
— педагогика сотрудничества (учебный диалог);
Список использованной литературы.
2. Истомина Н.Б. Рабочая тетрадь к учебнику «Математика» для 1 класса
3. Методические рекомендации к учебнику «Математика» 1 класс, под ред. Н.Б.Истоминой.- Смоленск: «Ассоциация ХХI век». 2006 год.
Ход урока
1. Оргмомент
Слайд 1. Звучит голос И.Левитана с сообщением о первом полёте человека в космос.
Учитель: Дети, 2011 год объявлен в нашей стране годом Российской космонавтики. А кто из вас интересуется космосом? Кто хочет полететь в космос? Сегодня представляется такая возможность для всего класса. Мы совершим учебный полёт. Чтобы не совершать ошибок во время полёта, нужно подготовиться, восстановить некоторые знания. Как вы думаете, что нам необходимо вспомнить?
Дети: Повторить числа, сложение и вычитание.
Учитель: Я соглашусь с вами, дети. Добавлю: нужно знать пройденные геометрические фигуры.
2. Актуализация прежних знаний
Учитель: На ваших столах лежат «Учебные маршрутные листы». Все результаты работы на уроке будем заносить на эти листы.
Итак, первое задание: «математический диктант». Прослушайте условие, высчитайте в уме, запишите только ответ.
Из 9 планет солнечной системы только две имеют женские имена. А сколько мужских имён в названиях планет солнечной системы? (7)
У созвездии «Большая медведица» 7 ярких звёзд. А в созвездии «Кассиопея» 5 ярких звёзд. На сколько больше ярких звёзд в созвездии Большая медведица? (2)
На мой вопрос в начале урока: «Кто мечтает полететь в космос?» ответили «да» 3 девочки и 7 мальчиков. Сколько всего ребят нашего класса хотят слетать в космос? (10)
Почему вторая фигура называется треугольником? (имеет три вершины и три стороны)
Учитель: В «Учебном маршрутном листе» найдите красную точку и постройте луч. Какой инструмент необходим? (Линейка)
Соедините две синие точки. Какая фигура у вас получилась? (Отрезок)
Через жёлтую точку проведите прямую линию. Можете провести ещё одну? А ещё? (Да!)
Верно, через одну единственную точку можно провести бесчисленное количество прямых линий.
3. Физкультминутка (Ребята выполняют упражнения, стоя у парт)
Раз, два!
Скорость света!
Три, четыре!
Мы летим!
На далёкие планеты
Поскорей попасть хотим!
Чтоб водить корабли,
Чтобы в небо взлететь,
Надо многое знать.
Надо много уметь!
И при этом, и при этом
Вы заметьте-ка,
Очень важная наука
Ма-те-ма-ти-ка!
4. Введение нового материала
Сегодня мы продолжаем путешествие в страну Геометрию.
Посмотрите, что у меня в руках? (Вермишель спагетти)
Какую геометрическую фигуру она вам напоминает? (Прямую линию)
Возьмите в руки спагетти, которые раздал вам дежурный. Переломите в середине, а затем каждую часть ещё раз переломите пополам.
Какие геометрические фигуры вам напоминают? (Отрезки, их получилось 4)
Соедините их кусочками пластилина между собой. Можно ли теперь назвать полученную фигуру прямой линией? (Нет)
Как бы вы назвали такую геометрическую фигуру? (Поломанная линия)
Я должна немного поправить вас, она называется «ломаная» линия.
Посмотрите, из чего состоит ломаная линия? (Из отрезков)
Звенья ломаной не лежат на одной прямой. Конец одного звена является началом другого. Место, где соединяются два звена, называется вершиной.
Сколько вершин у данной ломаной линии? (Три)
Кроме того, у ломаной линии есть 2 конца.
6. Первичное закрепление
Учитель: Дети, давайте вспомним ещё раз, какими бывают кривые линии? (Замкнутыми и незамкнутыми)
А как вы думаете, ломаные линии могут быть замкнутыми и незамкнутыми?
Учитель открывает на доске таблицу № 1:
— Какие фигуры изображены в таблице? (ломаные линии)
— У какой ломаной больше всего звеньев? (№ 4)
— У какой ломаной меньше всего звеньев? (№ 1)
— Какая ломаная имеет три вершины? (№ 2)
— Какая ломаная имеет пять вершин? (№ 4)
Учитель открывает на доске таблицу №2:
Учитель: Это тоже ломаные линии. Чем они отличаются от ломаных линий на первой таблице? (Все звенья соединены между собой)
— Назовите замкнутую ломаную линию, которая имеет меньше всего звеньев. (№1)
Верно, а может ли быть замкнутая линия из двух звеньев, подумайте. Давайте построим такую ломаную линию. (Нет, чтобы «замкнуть» линию нужно третье звено)
Учитель: Найдите и назовите на карте звёздного неба созвездия: незамкнутые ломаные линии и замкнутые.
Учитель: Если вашу «ломаную линию из спагетти» лежащую на парте, перевернуть, то будет напоминать созвездие «Кассиопею». Она была названа в честь царицы, которую заколдовала коварная колдунья.
7. Физкультминутка.
Для глаз. Дети следят за движением Колобка на Слайде№4
Задание на внимание
На несколько секунд я покажу вам одну фигуру. Вы должны запомнить её и выложить из счётных палочек точно такую.
Теперь поработайте в парах. Проверьте внимание своего одноклассника.
Какая фигура у вас получилась?
Что вы ещё скажете о ней? Можно ли её назвать ломаной линией?
Можно ли назвать её замкнутой? (незамкнутой?) Почему?
8. Подведение итога урока
С какой геометрической фигурой познакомились? (Ломаной линией)
Из каких элементов состоит ломаная линия? (Из звеньев и вершин)
Какие бывают ломаные линии? (Замкнутые и незамкнутые)
Переверните «Учебный маршрутный лист». Обведите цветным карандашом только ломаные линии, замкнутые и незамкнутые:
Какую линию описал корабль Ю.Гагарина за 108 минут вокруг Земли? (незамкнутую кривую линию)
В правом нижнем уголке «Учебного маршрутного листа» вам «улыбается» звёздочка. Какую геометрическую фигуру она напоминает? (Замкнутую ломаную линию) Определите количество вершин? Звеньев? Есть ли концы?
Самооценка работы учащихся на уроке:
Линия
Линия — это геометрическая фигура, образованная множеством точек, последовательно расположенных друг за другом.
Любую линию можно представить как след от точки, перемещающейся по данному пути. Например, грифель карандаша при прикосновении к бумаге оставляет на ней точку (1), но если грифелем провести по бумаге, то получится линия — последовательность точек, расположенных друг за другом (2):
Геометрические линии не имеют толщины.
Виды линий
Геометрические линии делятся на три вида:




























 Ломаной называется особая разновидность геометрической фигуры, которая составлена из нескольких отрезков. Эти отрезки последовательно соединены между собой своими концами. Конец каждого отрезка, за исключением последнего, является начальной точкой следующего. Смежные отрезки не должны находиться на одной прямой линии.
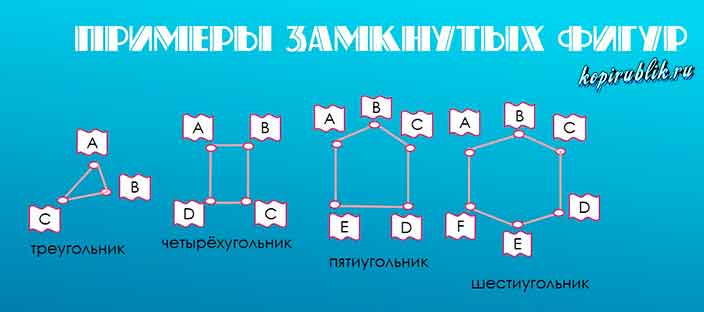
Ломаной называется особая разновидность геометрической фигуры, которая составлена из нескольких отрезков. Эти отрезки последовательно соединены между собой своими концами. Конец каждого отрезка, за исключением последнего, является начальной точкой следующего. Смежные отрезки не должны находиться на одной прямой линии. Количество звеньев или сторон в каждом многоугольнике соответствует количеству углов в нем же. Замкнутая ломаная из трех отрезков называется треугольником. Ломаная из четырех звеньев получила название четырехугольника. Фигура из пяти отрезков — пятиугольник и т. д.
Количество звеньев или сторон в каждом многоугольнике соответствует количеству углов в нем же. Замкнутая ломаная из трех отрезков называется треугольником. Ломаная из четырех звеньев получила название четырехугольника. Фигура из пяти отрезков — пятиугольник и т. д.