Что такое нижняя граница медианного интервала
Медиана
В статистических исследованиях довольно широко применяются средние величины. Их нахождение позволяет выявить типичное значение признака исследуемой совокупности. Например, типичный уровень доходов покупателей или возраст большинства клиентов компании. При этом вычисление, к примеру, среднего арифметического не всегда уместно.
Представим такую ситуацию: мы опросили 10 человек на предмет их уровня доходов. У 9-х доходы оказались примерно одинаковыми и составили 10 тыс. руб. Что касается 10-ого опрошенного, то оказалось, что его доход равняется 410 тыс. руб. в месяц. Если мы вычислим простое среднее арифметическое, то типичный доход будет равняться 50 тыс. руб.! Но это явно не так. В таких ситуациях более объективную и правдоподобную картину дает вычисление моды или медианы, которые относятся к структурным средним показателям.
Понятие медианы
Медиана (Me) — значение признака в исследуемом ряду величин, которое делит этот ряд на две равные части.
То есть половина (50%) всех значений в исследуемом ряду будет меньше медианы, а другая половина — больше ее. Поэтому медиану еще называют 50-й перцентиль или квантиль 0,5.
Формула для расчета медианы
Если значений немного, то медиану можно определить «на глазок». Для этого достаточно расположить все значения в порядке возрастания и найти середину.
Если число случаев четное и в центре ряда находятся два разных числа, то медианой будет среднее между ними (даже если такого значения нет в самом ряду исследуемых случаев). Например, в ряду 1 2 3 4 5 6, медианой будет 3,5.
Для нахождения медианы в более сложных случаях (по интервальным рядам) используется специальная формула:
Xme — нижняя граница медианного интервала (того интервала, накопленная частота которого превышает полусумму всех частот);
ime — величина медианного интервала;
f — частота (сколько раз в ряду встречается то или иное значение);
Sme-1 — сумма частот интервалов предшествующих медианному интервалу;
fme — число значений в медианном интервале (его частота).
Пример вычисления медианы
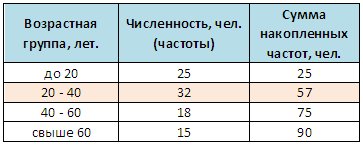
Был проведен опрос среди покупателей с целью выяснить их типичный возраст. По результатам опроса было установлено, что: 25 покупателей имеют возраст до 20 лет; 32 покупателя — 20-40 лет; 18 покупателей — 40-60 лет; 15 покупателей — свыше 60 лет. Найдем медиану.
Сначала находим медианный интервал. Для этого вычисляем сумму частот: 25 + 32 + 18 + 15 = 90. Половина этой суммы — 45. Это соответствует возрастной группе 20-40 лет (т. к. полученная полусумма частот — 45, и накопленная частота 1-й группы меньше ее, а 3-ей — больше). Тогда нижняя граница медианного интервала — 20 (лет), а величина медианного интервала — 20 (40 лет за вычетом 20). Сумма частот интервалов предшествующих медианному интервалу — 25. Число значений в медианном интервале — 32 (количество покупателей в возрасте 20-40 лет).
Расчетное значение медианы — 32,5. Округив его, получим средний возраст покупателя — 33 года.
Область применения медианы
При вычислении типичного признака неоднородных рядов, имеющих «выбросы» — значения во много раз отличающиеся от других значений ряда.
Особенности медианы
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.
Пример расчета медианы
Пример расчета медианы
План (содержание) работы Пример расчета медианы:
Понятие медианы
Формула расчета медианы
Применяемая для расчета медианы формула зависит от типа ряда распределения. Например, в неинтервальном ряду с четным количеством наблюдений медиана будет являться средним арифметическим значением из двух центральных величин, т.е. если совокупность состоит из десяти элементов, то искомый показатель будет равняться среднему значению пятого и шестого элемента. В случае, когда ряд неинтервальный и количество наблюдений нечетное, то медианным будет значение признака, находящегося в центре ранжированного ряда, т.е. для 11 элементов это будет шестой элемент.
В интервальном ряду распределения для вычисления медианы используют следующую формулу:
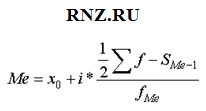
В том случае, если вариационный ряд является дискретным, то медианным будет величина признака в той группе, в которой накопленные частоты превысили половину количества единиц исследуемой совокупности.
Пример расчета медианы в интервальном вариационном ряду
В качестве исходных данных для расчета и анализа медианы используем статистическую группировку банков по величине собственных средств. Таким образом, расчет искомого показателя осуществим на основе следующего интервального ряда распределения:
Структурные характеристики вариационного ряда распределения
8.2. Медиана, квартили, децили
Значения изучаемого признака всех единиц статистической совокупности можно расположить в порядке возрастания (или убывания). В этом случае мы получим ранжированный ряд. Если число единиц совокупности нечетное, то значение признака, находящееся в середине ранжированного ряда, будет являться медианой. Если число единиц совокупности четное, то медианой будет средняя величина из двух значений признака, находящихся в середине ряда.
Пример 8.5. Имеются следующие данные о результатах сдачи экзамена по статистике в студенческой группе:
| Номер студента | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Оценка по статистике | 3 | 4 | 2 | 3 | 4 | 4 | 4 | 3 | 4 | 5 | 5 |
Представим их в виде ранжированного ряда:
| Номер студента | 3 | 1 | 4 | 8 | 2 | 5 | 6 | 7 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Оценка по статистике | 2 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 5 | 5 |
Пример 8.6. Имеются данные о цене антоновских яблок в шести магазинах города. Представим их сразу в виде ранжированного ряда:
| Название магазина | «Огонек» | «Маяк» | «Заря» | «Татьяна» | «Ночной» | «Любимый» |
|---|---|---|---|---|---|---|
| Цена яблок, руб. за кг | 40 | 41 | 42 | 44 | 44 | 45 |
В середине ранжированного ряда находятся цены двух магазинов, причем они разные. Медиана определяется как средняя величина из этих значений признака. Она равна 43 руб. [(42 + 44) : 2 = 43].
Способы расчета рассматриваемых структурных показателей зависят от вида вариационного ряда. Рассмотрим их подробнее.
8.2.1. Определение структурных средних в дискретных вариационных рядах
Для определения медианы в дискретных вариационных рядах:
Пример 8.7. Определим медианный стаж сотрудников страховой компании на основе следующих данных:
| Время работы, лет, xi | Число сотрудников, чел., fi | Накопленная частота, Si |
|---|---|---|
| 1 | 5 | 5 |
| 2 | 7 | 12 |
| 3 | 4 | 16 |
| 4 | 9 | 25 |
| 5 | 13 | 38 |
| 6 | 10 | 48 |
| 7 | 16 | 64 |
| 8 | 13 | 77 |
| Итого | 77 | — |
Номер медианы равен
Квартили и децили определяют аналогично медиане: сначала находят их номер, затем среди накопленных частот ищут такую, которая первая равна или превышает порядковый номер показателя, ей соответствует варианта, которая является искомым показателем. Номера квартилей рассчитываются по формулам:
Порядковые номера децилей исчисляются следующим образом:
Определим квартили по данным примера 8.7. Их номера равны:
Аналогично определяются децили. Например, восьмой дециль вычисляется следующим образом:
8.2.2. Определение структурных средних в интервальном вариационном ряду
В интервальных рядах сначала определяют медианный интервал. Для этого так же, как и в дискретных рядах, рассчитывают порядковый номер медианы
Накопленной частоте, которая равна номеру медианы или первая его превышает, в интервальном вариационном ряду соответствует медианный интервал. Обозначим эту накопленную частоту SМе. Непосредственно расчет медианы проводят по формуле:
Пример 8.8. По следующим данным определим медианное значение суммы выданных банками кредитов:
| Сумма выданных кредитов, млн ден. ед. | Количество банков, fi | Накопленная частота, Si. |
|---|---|---|
| 20-40 | 8 | 8 |
| 40-60 | 15 | 23 |
| 60-80 | 21 | 44 |
| 80-100 | 12 | 56 |
| 100-120 | 9 | 65 |
| 120-140 | 7 | 72 |
| 140-160 | 4 | 76 |
| Итого | 76 | — |
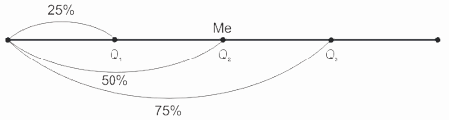
т.е. у 50% банков сумма выданных кредитов не превышает 74,286 млн ден. ед.
Далее произведем расчет квартилей и децилей в интервальном вариационном ряду.
Для приведенного интервального ряда необходимо определить:
тогда ей соответствует интервал «40-60», в котором находится первый квартиль;
тогда ей соответствует интервал «100-120», в котором находится третий квартиль;
т.е. у 25% банков сумма выданных кредитов не превышает 54,7 млн ден. ед.;
т.е. у 75% банков сумма выданных кредитов не превышает 102,2 млн ден. ед.
Аналогично квартилям определяем децили. Формулы, используемые в ходе расчетов, поместим в таблицу.
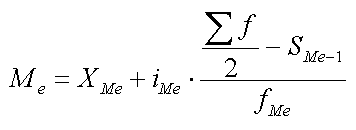
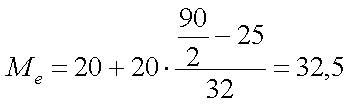

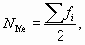
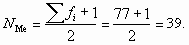
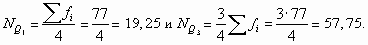






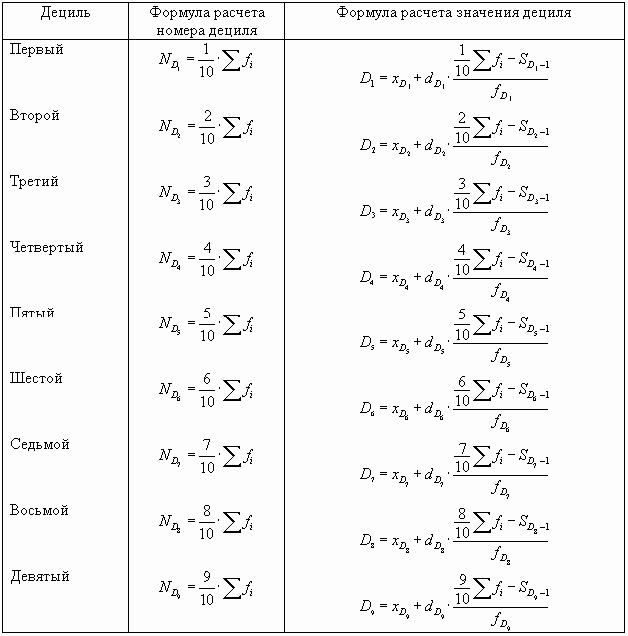
 следовательно SQ6 = 56, этой накопленной частоте соответствует интервал «80-100», в котором находится шестой дециль. Величина децильного значения равна:
следовательно SQ6 = 56, этой накопленной частоте соответствует интервал «80-100», в котором находится шестой дециль. Величина децильного значения равна:  (млн ден. ед.), т.д. у 60% банков сумма выданных кредитов не превышает 82,7 млн ден. ед.
(млн ден. ед.), т.д. у 60% банков сумма выданных кредитов не превышает 82,7 млн ден. ед.

 (8.17 – формула Медианы)
(8.17 – формула Медианы)
