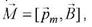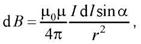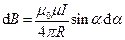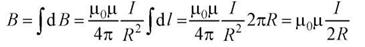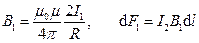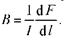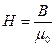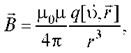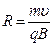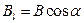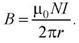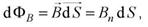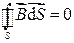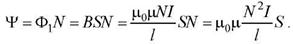Что такое нормаль к рамке
Рамка с током. Направление магнитного поля.
Аналогично тому, как при исследовании электростатического поля использовался точечный пробный заряд, при исследовании магнитного поля используется замкнутый плоский контур с током (рамка с током), линейные размеры которого малы по сравнению с расстоянием до токов, образующих магнитное поле.
Ориентация контура в пространстве характеризуется направлением нормали n к контуру.

За положительное направление нормали принимается направление поступательного движения правого винта, головка которого вращается в направлении тока, текущего в рамке.
Магнитное поле оказывает на рамку с током ориентирующее действие, поворачивая её определенным образом. Это свойство используется для выбора направления магнитного поля.
За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положительная нормаль к свободно подвешенной рамке с током, или направление, совпадающее с направлением силы, действующей на северный полюс (N) магнитной стрелки, помещенный в данную точку поля.
3. Вектор магнитной индукции.
Вращающий момент сил зависит как от свойств поля в данной точке, так и от свойств рамки с током и определяется векторным произведением
Для плоского контура с током / магнитный момент определяется как
Если в данную точку магнитного поля помещать рамки с различными магнитными моментами, то на них действуют различные вращающие моменты, но отношение 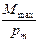
4. Макротоки и микротоки.
В дальнейшем мы будем различать макроскопические токи, т.е. электрические токи, протекающие по проводникам в электрических цепях и микроскопические токи, обусловленных движением электронов в атомах и молекулах.
Намагниченность постоянных магнитов является следствием существованием в них микротоков.
Внешнее магнитное поле оказывает ориентирующее, упорядочивающее действие на эти микротоки. Например, если вблизи какого-то тела поместить проводник с током (макроток), то под действием его магнитного поля микротоки во всех атомах определенным образом ориентируются, создавая в теле дополнительное магнитное поле.
Вектор магнитной индукции 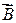
Поэтому, при одном и том же макротоке, вектор 
Магнитное поле макротока описывается вектором напряженности магнитного поля
В среде магнитное поле макротоков усиливается за счет поля микротоков среды.
5. Связь между 
Для однородной изотропной среды вектор магнитной индукции
где 

среды (п.39), безразмерная величина, показывающая, во сколько раз магнитное поле макротоков Н усиливается за счет поля микротоков среды.
6. Подобие векторных характеристик электростатического и магнитного полей.
Вектор магнитной индукции 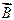

Аналогомвектора электрического смещения 

Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций полей, создаваемых каждым током или движущимся зарядом.
7. Закон Био-Савара-Лапласа.



Где 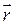

Направление 
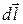


где α - угол между векторами 
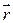
8. Магнитное поле прямого тока.
Из рисунка 
Следовательно
Угол α для всех элементов прямого провода
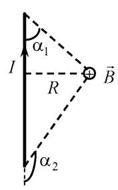

Если ток течет по отрезку провода (см. рисунок), то
Эта формула переходит в формулу для бесконечного длинного проводника при 
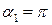
9. Магнитное поле в центре кругового тока.
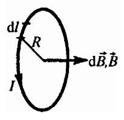
Можно показать, что на расстоянии r от центра витка вдоль оси витка магнитное поле будет равно
Напряженность магнитного поля, создаваемого круговым током, на большом расстоянии от витка стоком (r >> R)

Очевидное подобие этих формул объясняет, почему часто говорят, что контур с током подобен «магнитному диполю», имеющему равный с контуром магнитный момент.
где 

Наглядно направление силы Ампера принято определять по правилу левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор 
11. Взаимодействие параллельных токов.
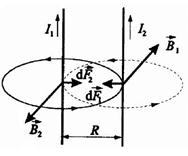
Два параллельных проводника с токами I1 и I2 находятся на расстоянии R друг от друга. Направление сил 


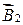
Отсюда: 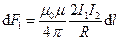

12. Магнитная постоянная.
В вакууме (µ=1) сила взаимодействия на единицу длины проводника
При 
Отсюда
13. Единицы магнитной индукции и напряженности магнитного поля.
Пусть элемент проводника dl с током I перпендикулярен направлению магнитного поля. Закон Ампера dF = IBdl, откуда
Из формулы 
напряженность такого поля, индукция которого в вакууме равна 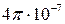
14. Магнитное поле свободно движущегося заряда.
Так же как и на проводник с током, магнитное поле действует и на отдельный заряд, движущийся в магнитном поле.
Сила, действующая на электрический заряд q, движущийся в магнитном поле 

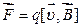
где α- угол между 
Сводная таблица.

Постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.
Движение заряда, на который кроме магнитного поля с индукцией 
16. Движение заряженных частиц в магнитном поле.
Считаем, что магнитное поле однородно и на частицы не действуют электрические поля. Рассмотрим три возможных случая:
1. 
магнитной индукции (угол α между векторами 


2. 
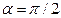
Сила Лоренца 
частицы. Частица будет двигаться по окружности радиуса R с центростремительным ускорением 

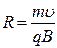
3.Заряженная частица движется под углом α к линиям магнитной
Движение частицы можно представить в виде суммы двух движений.
1)равномерного прямолинейного движения вдоль поля со скоростью
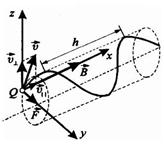
Суммарное движение будет движением по спирали, ось которой параллельна магнитному полю. Шаг винтовой линии 

Если магнитное поле неоднородно и заряженная частица движется под углом к линиям магнитного поля в направлении возрастания поля, то величины R и h уменьшаются с ростом 

Знак постоянной Холла 
18. Теорема о циркуляции вектора

где 
Теорема о циркуляции вектора 
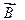

Эта теорема справедлива только для поля в вакууме, поскольку для поля в веществе надо учитывать молекулярные токи. Каждый ток учитывается столько раз, сколько он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта.

В каждой точке этой окружности вектор 
отсюда
Сравним выражения для циркуляций векторов 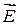
Принципиальное различие между этими формулами в том, что циркуляция вектора 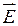

19. Магнитное поле соленоида.


На участках АВ и CD контур перпендикулярен линиям магнитной индукции, следовательно 
r 3 ). На участке DA контур совпадает с линией магнитной индукции, внутри соленоида поле однородно ( 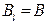
Магнитная индукция (бесконечного) соленоида в вакууме
20. Магнитное поле тороида в вакууме.
Магнитное поле отсутствует вне тороида, а внутри его оно является однородным.

21. Поток вектора магнитной индукции.
Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, равная
где 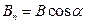
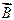
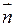
Поток вектора 
Поток вектора 
Поток вектора магнитной индукции через произвольную поверхность S
Если поле однородно и перпендикулярно ему расположена плоская поверхность с площадью S, то
22. Теорема Гаусса для магнитного поля в вакууме
Поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю
Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала ни конца и являются замкнутыми.
Магнитный поток через поверхность, ограниченную замкнутым контуром, называется потокосцеплением 
Потокосцепление контура, обусловленное магнитным полем тока в самом этом контуре, называется потокосцеплением самоиндукции.
Например, найдем потокосцепление самоиндукции соленоида с сердечником с магнитной проницаемостью µ. Магнитный поток сквозь один
виток соленоида площадью S равен 
сцепленный со всеми витками соленоида равен
Потокосцепление контура, обусловленное магнитным полем тока, идущего в другом контуре, называется потокосцеплением взаимной индукции этих двух контуров.
24. Работа по перемещению проводника с током в магнитном поле.
Под ее действием проводник переместился из положения 1 в положение 2.
Работа, совершаемая магнитным полем:
Работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.
25. Работа по перемещению контура с током в магнитном поле.
сумме работ по перемещению проводников ABC (dAl) и CDA (dА2), т.е.
При перемещении участка CDA силы Ампера направлены в сторону перемещения (образуют с направлением перемещения острые углы), поэтому dА2 >0
Силы, действующие на участок ABC контура, направлены против перемещения (образуют с направлением перемещения тупые углы), поэтому dА1 > R0) ЭДС самоиндукции 

При замыкании цепи помимо внешней ЭДС 
Самоиндукции 

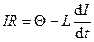

где 
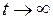
Таким образом, при включении источника тока сила тока возрастает по экспоненциальному закону (а не мгновенно).
34. Взаимная индукция

Рассмотрим два неподвижных контура 1 и 2 с токами I1 и I2, расположенных достаточно близко друг от друга. При протекании в контуре 1 тока I1 магнитный поток пронизывает второй контур
Коэффициенты пропорциональности L21 и L12 равны друг другу L12 = L2l = L и называются взаимной индуктивностью контуров.
При изменении силы тока в одном из контуров, в другом индуцируется
Взаимная индуктивность контуров зависит от геометрической формы, размеров, взаимного расположения контуров и от магнитной проницаемости окружающей контуры среды.
Для примера рассчитаем взаимную индуктивность двух катушек, намотанных на тороидальный сердечник.


Данное устройство является примером трансформатора.
Кроме орбитальных моментов, электрон обладает собственным механическим моментом импульса Ls, называемый спином.
Спину электрона соответствует собственный (спиновый) магнитный момент 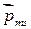

единицей магнитного момента электрона.
Общий магнитный момент атома или молекулы равен векторной сумме магнитных моментов (орбитальных и спиновых) входящих в атом (молекулу) электронов
Магнитные моменты атомных ядер в тысячи раз меньше магнитных моментов электронов, поэтому ими как правило пренебрегают.
38.Диа- и парамагнетики.

На вращающийся по орбите электрон, как на замкнутый ток, в магнитном поле действует вращающий момент сил. В результате электрон получает дополнительное равномерное вращение, при котором вектор 
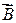
Теорема Лармора: действие магнитного поля на электронную орбиту можно свести ксообщению этой орбите прецессии с угловой скоростью
Прецессионное движение электронных орбит эквивалентно круговому микротоку. Так как этот микроток индуцирован внешним магнитным полем, то, согласно правилу Ленца, у атома появляется магнитный момент, направленный против внешнего поля.
Наведенные составляющие магнитных полей атомов складываются и образуют собственное магнитное поле вещества, ослабляющее внешнее магнитное поле. Этот эффект получил название диамагнитного эффекта, а вещества, намагничивающиеся во внешнем магнитном поле против направления поля, называются диамагнетиками (например, Ag, Au, Си. ).
Так как диамагнитный эффект обусловлен действием внешнего магнитного поля на электроны атомов вещества, то диамагнетизм свойствен всем веществам.
У парамагнитных веществ при отсутствии внешнего магнитного поля магнитные моменты электронов не компенсируют друг друга, и молекулы парамагнетиков всегда обладают магнитным моментом (такие молекулы называются полярными).
Вследствие теплового движения молекул их магнитные моменты ориентированы беспорядочно, поэтому, в отсутствие магнитного поля, парамагнитные вещества магнитными свойствами не обладают.
При внесении парамагнетика во внешнее магнитное поле устанавливается преимущественная ориентация магнитных моментов атомов (молекул) по полю (полной ориентации препятствует тепловое движение атомов).
Дата добавления: 2014-10-31 ; просмотров: 536 ; Нарушение авторских прав