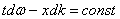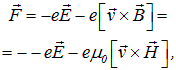Что такое нормальная дисперсия аномальная дисперсия
Дисперсия света: нормальная и аномальная.
 (или (или 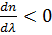 ) ) | (10.2.1) |
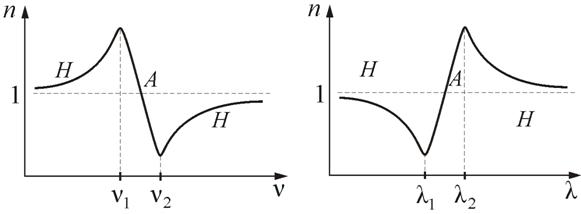
соответствуют нормальной дисперсии света(с ростом частоты ν показатель преломления n увеличивается). Нормальная дисперсия наблюдается у веществ, прозрачных для света. Например, обычное стекло прозрачно для видимого света, и в этой области частот наблюдается нормальная дисперсия света в стекле. На основе явления нормальной дисперсии основано «разложение» света стеклянной призмой монохроматоров.
Дисперсия называется аномальной, если
 | (или 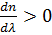 ), ), | (10.2.2) |
т.е. с ростом частоты ν показатель преломления n уменьшается. Аномальная дисперсия наблюдается в областях частот, соответствующих полосам интенсивного поглощения света в данной среде. Например, у обычного стекла в инфракрасной и ультрафиолетовой частях спектра наблюдается аномальная дисперсия.
Зависимости n от ν и λ показаны на рис. 10.4 и 10.5.
В зависимости от характера дисперсии групповая скорость u в веществе может быть как больше, так и меньше фазовой скорости υ (в недиспергирующей среде u=V).
Групповая скорость u связана с циклической частотой ω и волновым числом k соотношением: 


 . . | (10.2.3) |
Таким образом, при нормальной дисперсии u
При аномальной дисперсии u > υ, и, в частности, если 
34. Теория дисперсии
Дисперсиейсвета называется зависимость фазовой скорости света в среде от его частоты v.
Так как v=с/n, то дисперсией света можно назвать также зависимость показателя преломления n среды от частоты v световой волны.
Согласно электронной теории дисперсии справедлива следующая приближенная формула для показателя преломления


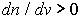

Область В, для которой с увеличением частоты v показатель преломления уменьшается называется областью аномальной дисперсии, т.е. для нее

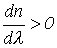
В области аномальной дисперсии поглощение света очень велико.
Групповая скорость
В результате суперпозиции нескольких синусоидальных волн образуется несинусоидальная волна с каким-то набором частот и волновых чисел. За скорость распространения такой волны в пространстве берётся скорость распространения фиксированной амплитуды. Но если в случае простой синусоидальной волны эта скорость совпадает со скоростью распространения фиксированной фазы (мы назвали эту скорость фазовой), то в случае сложной несинусоидальной волны сама амплитуда зависит от времени и координат (см. предыдущий пример). Амплитуда сложной волны есть:
Фиксированная амплитуда А будет удовлетворять условию:
Взяв полный дифференциал от этого выражения, получим (независимые координаты у нас x и t):
Скорость распространения фиксированной амплитуды в несинусоидальной волне получается следующей:
Эта скорость называется ГРУППОВОЙ СКОРОСТЬЮ волны. Она в общем случае отличается от фазовой скорости n:
Связь между этими скоростями можно легко получить (учтя зависимость частоты и волнового числа от длины волны):
Среда называется ДИСПЕРГИРУЮЩЕЙ, если в ней волны разной длины распространяются с разной скоростью. Зависимость скорости волны (фазовой) от длины волны (или, что то же самое, от частоты) называется ДИСПЕРСИЕЙ.
Видно, что групповая скорость будет совпадать с фазовой только в недиспергирующих средах, где составляющие сложной волны будут перемещаться с одинаковой скоростью, и сама сложная волна не будет менять своей формы (не будет «расплываться»).
Для МОНОХРОМАТИЧЕСКОЙ ВОЛНЫ (так называется простая синусоидальная волна, имеющая одну частоту) фазовая и групповая скорости всегда совпадают, даже в диспергирующих средах.
Фазовая скорость есть чисто абстрактное математическое понятие, эта скорость не связана с перемещением в пространстве чего-либо материального.
Групповая скорость связана с перемещением в пространстве возмущения фиксированной амплитуды; поскольку энергия волны связана с её амплитудой, групповая скорость есть скорость распространения энергии в пространстве.
В общем случае фазовая скорость может превышать скорость света (в случае, например, электромагнитной волны, или волн Де Бройля). Групповая же скорость, в полном согласии с теорией относительности, всегда меньше либо равна скорости света.
Дата добавления: 2018-02-15 ; просмотров: 4163 ; Мы поможем в написании вашей работы!
Что такое нормальная дисперсия аномальная дисперсия
Дисперсия света
§1 Способы наблюдения дисперсии.
Призматический и дифракционный спектры. Метод Рождественского.
Явление дисперсии заключается в том, что показатель преломления зависит от длины волны.

Спектр, показанный на рис. является призматическим. Фиолетовые волны преломляются сильнее красных, т.к. длина волны красных волн больше, чем у фиолетовых, а частота, соответственно, меньше, то показатель преломления красных волн будет меньше, чем у фиолетовых.
Дисперсия света называется нормальной, если показатель преломления монотонно убывает с увеличением длины волны (возрастает с увеличением частоты).

В случае дисперсия, если
дисперсия света называется аномальной.
Нормальная дисперсия света наблюдается вдали от собственных линий поглощения, аномальная – в пределах полос или линий поглощения.
Оптическая схема спектросенситометра ИСП-73: 1 — источник света (ленточная лампа накаливания); 2 — двухлинзовый конденсор; 3 — дисковый затвор с выдержками 0,05, 0,2 и 1,0 сек; 4 — револьверный диск с набором дырчатых диафрагм; 5 — входная щель спектрографа; 6 — объектив коллиматора; 7 — призмы; 8 — объектив камеры спектрографа. (Источник: БСЭ).
Для изучения нормальной и аномальной дисперсии можно использовать метод скрещенных призм.
Метод скрещенных призм нельзя использовать в том случае, если нас интересует n паров и газов, показатель преломления которых близок к 1. В этом случае Д.С. Рождественский предложил вместо призмы П1 поставить интерферометр Жамена, в одно из плеч которого помещается запаянная трубочка с газом, в другое – пластинки, дисперсия которой известна. Вместо призмы П2 ставят дифракционный или призматический спектрограф ( 
§2 Электронная теория дисперсии света.
Аномальная и нормальная дисперсия света. Связь дисперсии и поглощения
Макроскопическая теория Максвелла не может объяснить дисперсию света. Из теории Максвелла следует, что 
Явление дисперсии можно объяснить, рассматривая взаимодействие световой волны с веществом. Такое стало возможным благодаря классической электронной теории Лоренца.
Согласно классической электронной теории электроны в атоме совершают колебания под действием квазиупругой силы. Световая волн, падающая на диэлектрик, заставляет электроны, находящиеся в атоме этого диэлектрика, совершать вынужденные колебания, частота которых совпадает с частотой вынуждающей силы. Но электроны, движущиеся ускоренно излучают электромагнитные волны. Эти вторичны волны, излучаемые электронами атомов вещества, имеют ту же частоту, что и падающая волна. Начальные фазы могут различаться. Эти вторичные волны интерферируют с падающей волной, и в веществе распространяется результирующая волна, направление которой совпадает с направлением падающей волны, скорость которой зависит от частоты (а в вакууме равна скорости света). Следовательно, показатель преломления n зависит от частоты ω.
где χ – диэлектрическая восприимчивость вещества, Р – вектор поляризации (результирующий дипольный момент единицы объёма).
Согласно теории Максвелла

В условиях, когда на вещество падает световая волна, электрическое поле изменяется столь быстро, что поляризуемость (нас будет интересовать только электронная, т.е. индуцированная полем световой волны) не успевает изменяться за полем. В этом случае
где n 0 – количество атомов в единице объёма, РЕ – индуцированный дипольный момент одного атома. Можно показать, что наиболее сильному воздействию электрического поля световой волны подвергаются наиболее слабо связанные с ядром электроны, так называемые оптические электроны. Для простоты считаем, что каждый атом содержит один оптический электрон. Тогда
т.е. n зависит от смещения электронов в атоме, под действием поля световой волны. На электрон, находящийся в атоме действует также силы:
квазиупругая – из-за наличия связи электрона с ядром:
Вынуждающая сила со стороны световой волны
Под действием этих сил электрон начинает совершать вынужденные колебания
Для простоты рассмотрения будем пренебрегать затуханием колебаний. В этом случае

Если учесть затухание (β ≠ 0), то мы получаем формулу, которая даёт хорошее соответствие с экспериментальной кривой)
§3 Поглощение света.
Закон Бугера
Экспериментально было установлено, что свет, проходя через вещество поглощается. Особенно сильное поглощение наблюдается для тех длин волн, частоты которых совпадают с собственными частотами для данного вещества. Интенсивность света изменяется по закону:
где α – коэффициент поглощения,

Знак минус показывает, что dI и 

Коэффициент поглощения α есть величина обратная величине пути в данном веществе, проходя который, свет уменьшает свою интенсивность в е раз.
Если растворить поглощающие свет вещество в растворителе, который не поглощает данный цвет, то коэффициент поглощения раствора будет прямо пропорционален длине поглощающего вещества, т.е.
Для разряженных газов спектр поглощения является линейчатым. Для газа в молекулярном состоянии спектр поглощения является полосатым. Для твердых диэлектриков спектр поглощения сплошной в определенном интервале частот. Все другие частоты диэлектрик будет пропускать.
6.2. Дисперсия света
Дисперсия света — это зависимость показателя преломления n вещества от длины волны света (в вакууме)
или, что то же самое, зависимость фазовой скорости световых волн от частоты:
Дисперсией вещества называется производная от n по
Дисперсия — зависимость показателя преломления вещества от частоты волны – особенно ярко и красиво проявляет себя совместно с эффектом двойного лучепреломления (см. Видео 6.6 в предыдущем параграфе), наблюдаемом при прохождении света через анизотропные вещества. Дело в том, что показатели преломления обыкновенной и необыкновенной волн различно зависят от частоты волны. В результате цвет (частота) света прошедшего через анизотропное вещество помещенное между двумя поляризаторами зависит как от толщины слоя этого вещества, так и от угла между плоскостями пропускания поляризаторов.
Для всех прозрачных бесцветных веществ в видимой части спектра с уменьшением длины волны показатель преломления увеличивается, то есть дисперсия вещества отрицательна: 
Нормальная дисперсия вещества — это отрицательная дисперсия
Если вещество поглощает свет в каком-то диапазоне длин волн (частот), то в области поглощения дисперсия
оказывается положительной и называется аномальной (рис. 6.7, область 2–3).
Рис. 6.7. Зависимость квадрата показателя преломления (сплошная кривая) и коэффициента поглощения света веществом
(штриховая кривая) от длины волны l вблизи одной из полос поглощения (
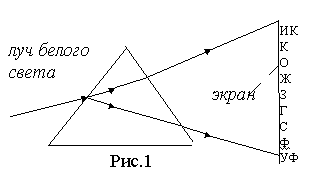
Изучением нормальной дисперсии занимался ещё Ньютон. Разложение белого света в спектр при прохождении сквозь призму является следствием дисперсии света. При прохождении пучка белого света через стеклянную призму на экране возникает разноцветный спектр (рис. 6.8).
Рис. 6.8. Прохождение белого света через призму: вследствие различия значений показателя преломления стекла для разных
длин волн пучок разлагается на монохроматические составляющие — на экране возникает спектр
Наибольшую длину волны и наименьший показатель преломления имеет красный свет, поэтому красные лучи отклоняются призмой меньше других. Рядом с ними будут лучи оранжевого, потом желтого, зеленого, голубого, синего и, наконец, фиолетового света. Произошло разложение падающего на призму сложного белого света на монохроматические составляющие (спектр).
Ярким примером дисперсии является радуга. Радуга наблюдается, если солнце находится за спиной наблюдателя. Красные и фиолетовые лучи преломляются сферическими капельками воды и отражаются от их внутренней поверхности. Красные лучи преломляются меньше и попадают в глаз наблюдателя от капелек, находящихся на большей высоте. Поэтому верхняя полоса радуги всегда оказывается красной (рис. 26.8).
Рис. 6.9. Возникновение радуги
Используя законы отражения и преломления света, можно рассчитать ход световых лучей при полном отражении и дисперсии в дождевых каплях. Оказывается, что лучи рассеиваются с наибольшей интенсивностью в направлении, образующем угол около 42° с направлением солнечных лучей (рис. 6.10).
Рис. 6.10. Расположение радуги
Геометрическое место таких точек представляет собой окружность с центром в точке 0. Часть ее скрыта от наблюдателя Р под горизонтом, дуга над горизонтом и есть видимая радуга. Возможно также двойное отражение лучей в дождевых каплях, приводящее к радуге второго порядка, яркость которой, естественно, меньше яркости основной радуги. Для нее теория дает угол 51°, то есть радуга второго порядка лежит вне основной. В ней порядок цветов заменен на обратный: внешняя дуга окрашена в фиолетовый цвет, а нижняя — в красный. Радуги третьего и высших порядков наблюдаются редко.
Элементарная теория дисперсии. Зависимость показателя преломления вещества от длины электромагнитной волны (частоты) объясняется на основе теории вынужденных колебаний. Строго говоря, движение электронов в атоме (молекуле) подчиняется законам квантовой механики. Однако для качественного понимания оптических явлений можно ограничиться представлением об электронах, связанных в атоме (молекуле) упругой силой. При отклонении от равновесного положения такие электроны начинают колебаться, постепенно теряя энергию на излучение электромагнитных волн или передавая свою энергию узлам решетки и нагревая вещество. В результате этого колебания будут затухающими.
При прохождении через вещество электромагнитная волна воздействует на каждый электрон с силой Лоренца:
где v — скорость колеблющегося электрона. В электромагнитной волне отношение напряженностей магнитного и электрического полей равно
Поэтому нетрудно оценить отношение электрической и магнитной сил, действующих на электрон:
Электроны в веществе движутся со скоростями, много меньшими скорости света в вакууме:
Таким образом, можно считать, что при прохождении через вещество электромагнитной волны на каждый электрон действует только электрическая сила:
где 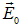

где, 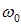
Следовательно, смещение электрона из положения равновесия пропорционально напряженности электрического поля. Смещениями ядер из положения равновесия можно пренебречь, так как массы ядер весьма велики по сравнению с массой электрона.
Атом со смещенным электроном приобретает дипольный момент
(для простоты положим пока, что в атоме имеется только один «оптический» электрон, смещение которого вносит определяющий вклад в поляризацию). Если в единице объема содержится N атомов, то поляризованность среды (дипольный момент единицы объема) можно записать в виде
В реальных средах возможны разные типы колебаний зарядов (групп электронов или ионов), вносящих вклад в поляризацию. Эти типы колебаний могут иметь разные величины заряда еi и массы тi, а также различные собственные частоты 
Безразмерный коэффициент пропорциональности fk характеризует эффективный вклад каждого типа колебаний в общую величину поляризации среды: