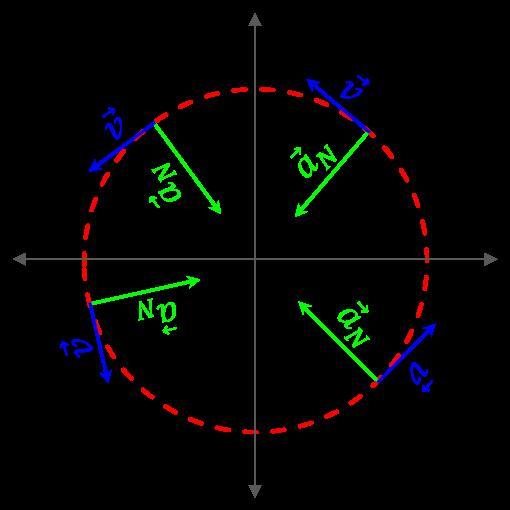
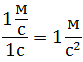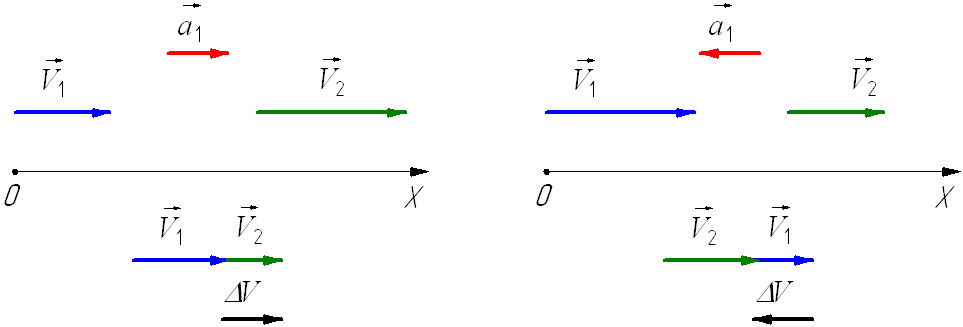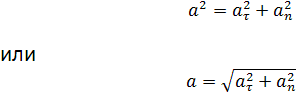Что такое нормальное ускорение
Общее определение
Вам будет интересно: Чваниться — это некультурная привычка: толкование слова
То есть для вычисления величины a¯ необходимо найти производную вектора скорости по времени в данный момент. Формула показывает, что a¯ измеряется в метрах в секунду в квадрате (м/с2).
Направление полного ускорения a¯ никак не связано с вектором v¯. Однако оно совпадает с вектором dv¯.
Причиной появления у движущихся тел ускорения является действующая на них внешняя сила любой природы. Ускорение никогда не возникает, если внешняя сила равна нулю. Направление действия силы совпадает с направлением ускорения a¯.
Криволинейная траектория
В общем случае рассмотренная величина a¯ имеет две составляющие: нормальную и касательную. Но прежде всего напомним, что такое траектория. В физике под траекторией понимают линию, вдоль которой тело проходит некоторый путь в процессе движения. Поскольку траектория может представлять собой либо прямую линию, либо кривую, то движение тел делится на два типа:
В первом случае вектор скорости тела может измениться только на противоположный. Во втором же случае вектор скорости и ее абсолютное значение изменяются постоянно.
Как известно, скорость направлена по касательной к траектории. Этот факт позволяет ввести следующую формулу:
a¯ = dv¯/dt = d(v * u¯)/dt = dv/dt * u¯ + v * du¯/dt.
Нормальное ускорение точки
Обозначим эту компоненту ускорения символом an¯. Запишем для нее выражение еще раз:
Уравнение нормального ускорения an¯ можно записать в явном виде, если провести следующие математические преобразования:
an¯ = v * du¯/dt = v * du¯/d l* dl/dt = v2/r * re¯.
Центростремительная и центробежная силы
Во всех названных примерах сила центростремительная приводит к изменению прямолинейной траектории. В свою очередь, ей препятствуют инерционные свойства тела. С ними связывают центробежную силу. Эта сила, действуя на тело, пытается «выбросить» его из криволинейной траектории. Например, когда авто делает поворот, то пассажиров прижимает к одной из дверей транспортного средства. Это и есть действие центробежной силы. Она, в отличие от центростремительной, является фиктивной.
Пример задачи
Как известно, наша Земля вращается по круговой орбите вокруг Солнца. Необходимо определить нормальное ускорение голубой планеты.
Для решения задачи воспользуемся формулой:
Из справочных данных находим, что линейная скорость v нашей планеты составляет 29,78 км/с. Расстояние r до нашей звезды равно 149 597 871 км. Переводя эти числа в метры в секунду и метры, соответственно, подставляя их в формулу, получаем ответ: an = 0,006 м/с2, что составляет 0,06 % от величины ускорения свободного падения на планете.
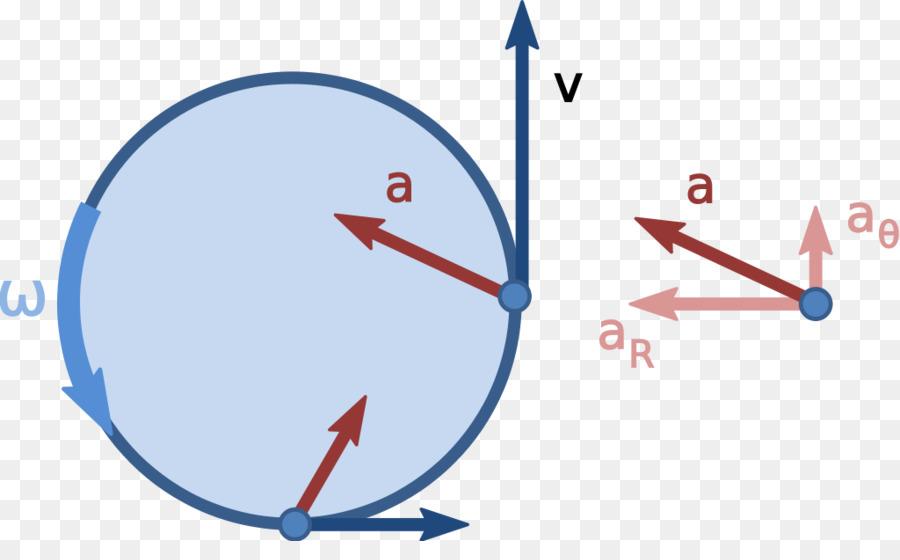
Нормальное и тангенциальное ускорение
Тангенциальным (касательным) ускорением называют ту составляющую вектора ускорения, которая направлена по касательной к траектории в данной точке траектории движения. Тангенциальное ускорение описывает степень изменения скорости по модулю при совершении криволинейного движения.
Если тело движется по криволинейной траектории, то его скорость направлена по касательной к этой траектории.
Так как направление скорости все время меняется, значит, в таком случае криволинейное движение всегда происходит с ускорением, также, если модуль скорости не меняется.
В большинстве случаев ускорение направлено под некоторым углом к скорости. Составляющую ускорения, которая направлена вдоль скорости, называют тангенциальным ускорением 
. Тангенциальное ускорение описывает степень изменения скорости по модулю:
Нормальное ускорение 
– это составляющая ускорения, которая направлена к центру кривизны траектории, то есть она является нормалью (направлена перпендикулярно) к скорости. Нормальное ускорение описывает степень изменения скорости по направлению:
Здесь R – это радиус кривизны траектории в заданной точке.
Тангенциальное и нормальное ускорение всегда имеют перпендикулярное направление, откуда получаем модуль полного ускорения:
.
Тангенциальное и нормальное ускорение. Касательное и нормальное ускорение
Изучение физики начинают с рассмотрения механического движения. В общем случае тела движутся по кривым траекториям с переменными скоростями. Для их описания используют понятие ускорения. В данной статье рассмотрим, что такое тангенциальное и нормальное ускорение.
Кинематические величины. Скорость и ускорение в физике
Вам будет интересно: Оборона Кавказа: история, ход боевых действий, награждение героев сражений, фото орденов и медалей
В случае движения по окружности используют аналогичные кинематические характеристики, которые приведены к центральному углу окружности.
Вам будет интересно: История основания Ростова-на-Дону: интересные факты, фото
Чем сильнее изменится скорость за интервал времени dt, тем больше будет ускорение.
Для понимания изложенной дальше информации необходимо помнить, что ускорение появляется в результате любого изменения скорости, включая изменения как ее модуля, так и ее направления.
Касательное и нормальное ускорение
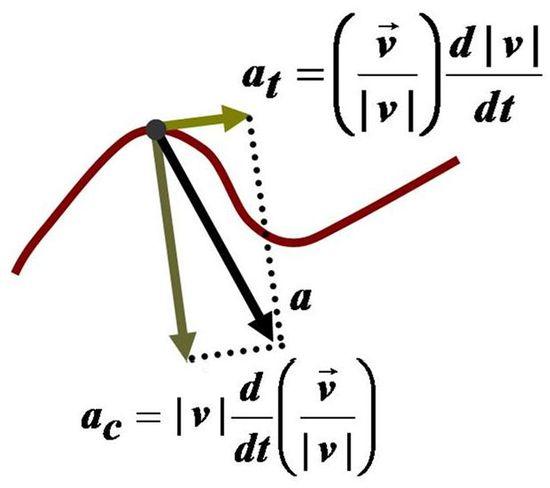
Чтобы вычислить вектор полного ускорения в момент времени t, необходимо найти производную скорости по времени. Имеем:
a¯ = dv¯ / dt = d (v × ut¯) / dt
Поскольку модуль скорости и единичный вектор изменяются со временем, то, пользуясь правилом нахождения производной от произведения функций, получаем:
a¯ = dv / dt × ut¯ + d (ut¯) / dt × v
Касательное ускорение
Еще раз запишем формулу для вычисления касательного ускорения:
Это равенство означает, что тангенциальное (касательное) ускорение направлено так же, как вектор скорости в любой точке траектории. Оно численно определяет изменение модуля скорости. Например, в случае прямолинейного движения полное ускорение состоит только из касательной составляющей. Нормальное ускорение при таком типе перемещения равно нулю.
Причиной появления величины at¯ является воздействие внешней силы на движущееся тело.
В случае вращения с постоянным угловым ускорением α тангенциальная составляющая ускорения может быть вычислена по следующей формуле:
Нормальное или центростремительное ускорение
Теперь выпишем еще раз вторую компоненту полного ускорения:
Из геометрических соображений можно показать, что производная единичного касательного к траектории вектора по времени равна отношению модуля скорости v к радиусу r в момент времени t. Тогда выражение выше запишется так:
Эта формула нормального ускорения свидетельствует, что оно, в отличие от касательной компоненты, не зависит от изменения скорости, а определяется квадратом модуля самой скорости. Также ac возрастает с уменьшением радиуса вращения при постоянной величине v.
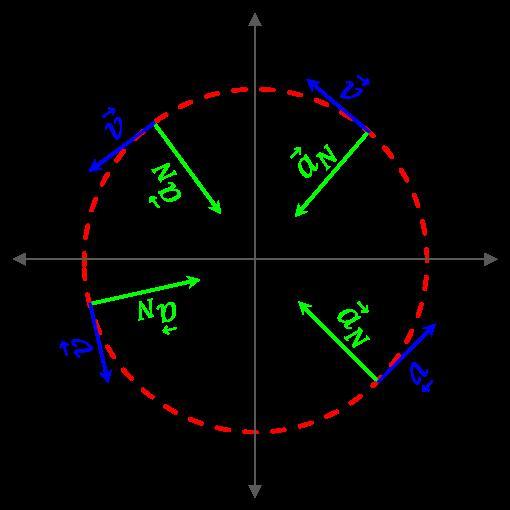
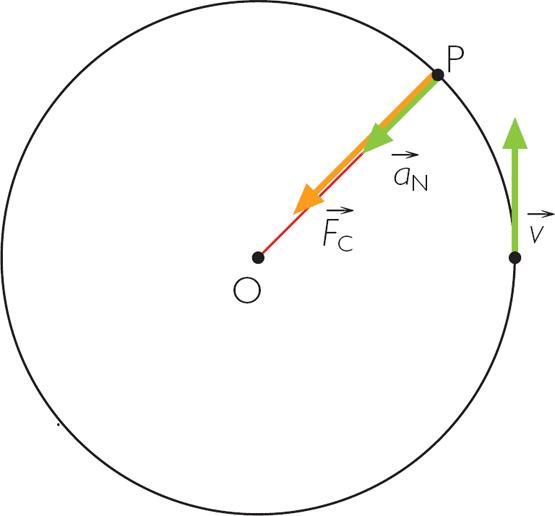
Нормальное ускорение называют центростремительным потому, что оно направлено от центра масс вращающегося тела к оси вращения.
Причиной появления этого ускорения является центральная компонента воздействующей на тело силы. Например, в случае вращения планет вокруг нашего Солнца центростремительной силой является гравитационное притяжение.
Нормальное ускорение тела изменяет только направление скорости. Оно не способно изменить ее модуль. Этот факт является важным его отличием от касательной компоненты полного ускорения.
Поскольку центростремительное ускорение возникает всегда, когда вектор скорости поворачивается, то оно существует также в случае равномерного вращения по окружности, при котором тангенциальное ускорение равно нулю.
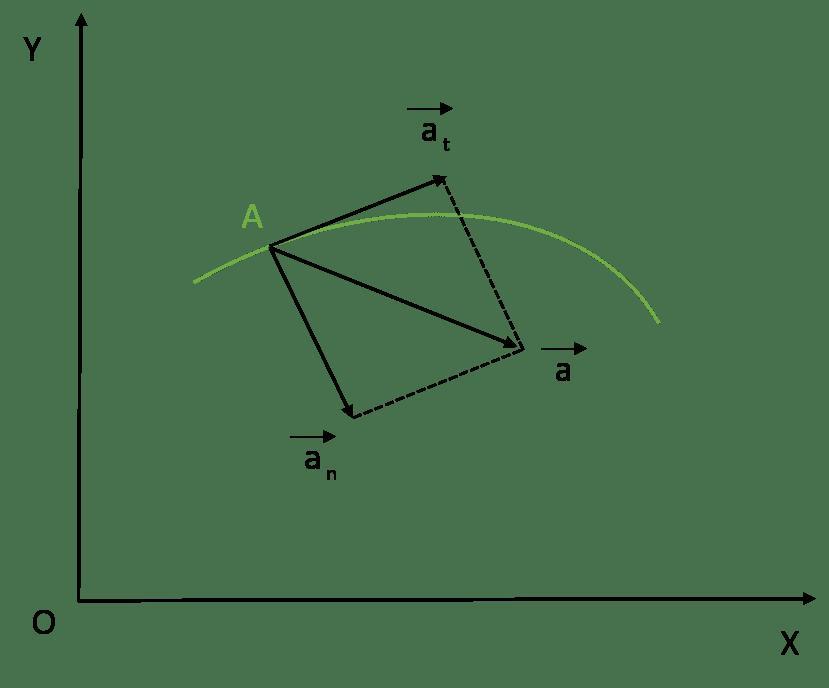
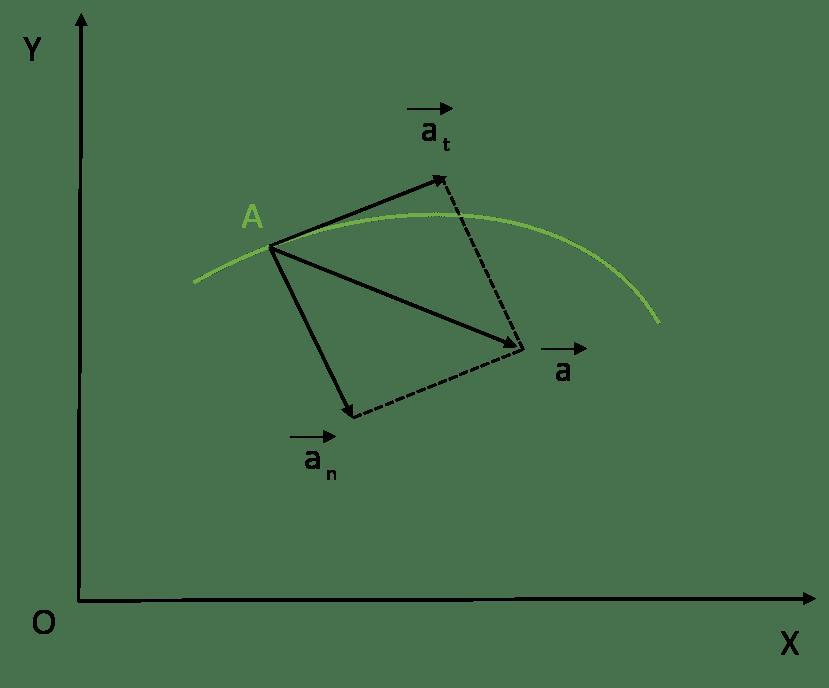
Модуль и направление полного ускорения
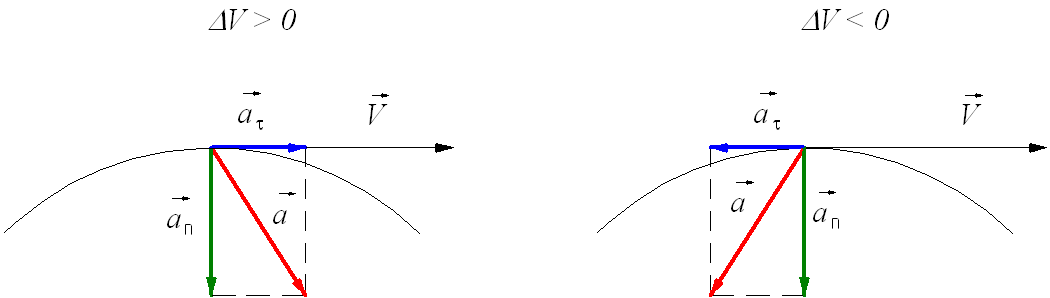
Итак, мы выяснили, что тангенциальная компонента рассматриваемой физической величины направлена по касательной к траектории движения. В свою очередь, нормальная компонента перпендикулярна траектории в данной точке. Это означает, что две компоненты ускорения перпендикулярны друг другу. Их векторное сложение дает вектор полного ускорения. Вычислить его модуль можно по следующей формуле:
Направление вектора a¯ можно определить как относительно вектора at¯, так и относительно ac¯. Для этого следует использовать соответствующую тригонометрическую функцию. Например, угол между полным и нормальным ускорениями равен:
Решение задачи на определение центростремительного ускорения
Колесо, которое имеет радиус 20 см, раскручивается с угловым ускорением 5 рад/с2 в течение 10 секунд. Необходимо определить нормальное ускорение точек, находящихся на периферии колеса, через указанное время.
Для решения задачи воспользуемся формулой связи между тангенциальным и угловым ускорениями. Получаем:
Поскольку равноускоренное движение длилось в течение времени t = 10 секунд, то приобретенная за это время линейная скорость была равна:
Полученную формулу подставляем в соответствующее выражение для нормального ускорения:
ac = v2 / r = α2 × t2 × r
Остается подставить известные значения в это равенство и записать ответ: ac = 500 м/с2.
Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
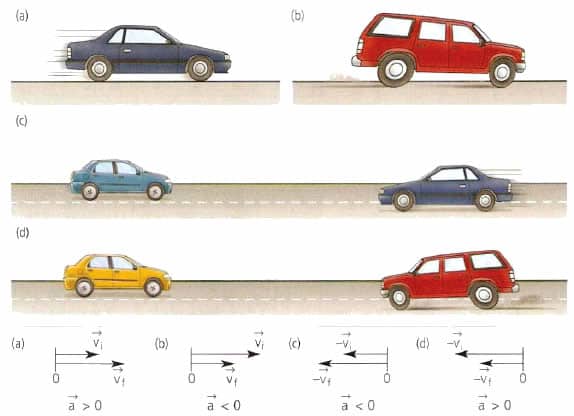
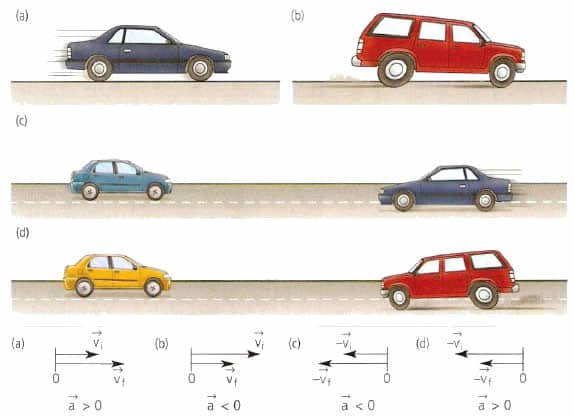
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
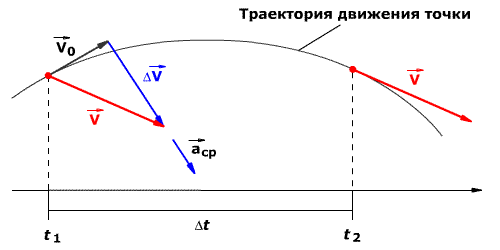
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
а направление вектора ускорения совпадает с вектором скорости 
Если скорость тела по модулю уменьшается, то есть
то направление вектора ускорения противоположно направлению вектора скорости 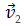Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а 
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения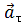 
(см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой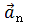 
Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
Понятия о скорости, тангенциальном и нормальном ускорениях. Формулы
Чтобы уметь решать различные задачи на движение тел по физике, необходимо знать определения физических величин, а также формулы, с помощью которых они связаны. В этой статье будут рассмотрены вопросы, что такое тангенциальная скорость, что такое полное ускорение и какие компоненты его составляют.
Понятие о скорости
Двумя основными величинами кинематики перемещения тел в пространстве являются скорость и ускорение. Скорость описывает быстроту перемещения, поэтому математическая форма записи для нее имеет следующий вид:
Вам будет интересно: Что такое туча? Определение
Как известно, всякое тело движется по воображаемой линии, которая называется траекторией. Вектор скорости всегда направлен по касательной к этой траектории, в какой бы точке не находилось движущееся тело.
Существует несколько названий величины v¯, если рассматривать ее совместно с траекторией. Так, поскольку направлена она по касательной, то ее называют тангенциальной скоростью. Также о ней могут говорить, как о линейной физической величине в противоположность угловой скорости.
Вычисляется скорость в метрах в секунду в СИ, однако на практике часто пользуются километрами в час.
Понятие об ускорении
Измеряется ускорение в м/с2. Например, известное всем ускорение свободного падения является тангенциальным при вертикальном подъеме или падении объекта. Его величина вблизи поверхности нашей планеты составляет 9,81 м/с2, то есть за каждую секунду падения скорость тела увеличивается на 9,81 м/с.
Причиной появления ускорения является не скорость, а сила. Если сила F оказывает действие на тело массой m, то она неминуемо создаст ускорение a, которое можно вычислить так:
Эта формула является прямым следствием из второго закона Ньютона.
Полное, нормальное и тангенциальное ускорения
Скорость и ускорение как физические величины были рассмотрены в предыдущих пунктах. Теперь мы подробнее изучим, какие компоненты составляют полное ускорение a¯.
Предположим, что тело движется со скоростью v¯ по криволинейной траектории. Тогда будет справедливо равенство:
Вектор u¯ имеет единичную длину и направлен вдоль касательной линии к траектории. Воспользовавшись таким представлением скорости v¯, получим равенство для полного ускорения:
a¯ = dv¯/dt = d(v*u¯)/dt = dv/dt*u¯ + v*du¯/dt.
Полученное в правом равенстве первое слагаемое называется тангенциальным ускорением. Скорость связана с ним тем фактом, что она количественно определяет изменение абсолютного значения величины v¯, не принимая во внимание ее направление.
Если обозначить как at и an тангенциальную и нормальную составляющие полного ускорения a, тогда модуль последнего можно вычислить по формуле:
Связь тангенциального ускорения и скорости
Соответствующую связь описывают кинематические выражения. Например, в случае движения по прямой с постоянным ускорением, которое является тангенциальным (нормальная составляющая равна нулю), справедливы выражения:
В случае движения по окружности с постоянным ускорением эти формулы так же справедливы.
Таким образом, какой бы ни была траектория перемещения тела, тангенциальное ускорение через тангенциальную скорость рассчитывается, как производная по времени от ее модуля, то есть:
Например, если скорость изменяется по закону v = 3*t3 + 4*t, тогда at будет равно:
Скорость и нормальное ускорение
Запишем в явном виде формулу для нормальной компоненты an, имеем:
an¯ = v*du¯/dt = v*du¯/dl*dl/dt = v2/r*re¯
Нормальное ускорение появляется всегда, когда изменяется вектор скорости, однако оно равно нулю, если этот вектор сохраняет направление. Говорить о величине an¯ имеет смысл только тогда, когда кривизна траектории является конечной величиной.
Выше мы отмечали, что при движении по прямой линии нормальное ускорение отсутствует. Однако в природе существует тип траектории, при движении по которой an имеет конечную величину, а at = 0 при |v¯| = const. Этой траекторией является окружность. Например, вращение с постоянной частотой металлического вала, карусели или планеты вокруг собственной оси происходит с постоянным нормальным ускорением an и нулевым тангенциальным ускорением at.