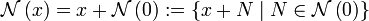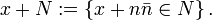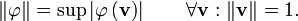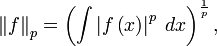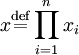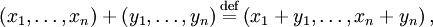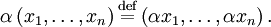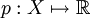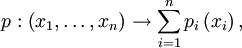Что такое нормированное пространство
Нормированные пространства
Содержание
Определение и примеры [ править ]
Приведём примеры норм для различных множеств:
Нормированным пространством называют пару [math](X, \|\cdot\|)[/math] из линейного пространства и нормы на нём.
Арифметика пределов [ править ]
В нормированных пространствах определение предела записывается аналогично пределу вещественной последовательности, отличаясь лишь заменой знака модуля на знак нормы.
Специфика нормированных пространств — структура линейного пространства на рассматриваемом множестве. То есть, точки пространства можно складывать и умножать на числа, и эти операции будут непрерывными по норме пространства.
Следует иметь ввиду, что метрическое пространство, наделённое структурой линейного, не обязательно можно нормировать (задать норму такую, что сходимость по метрике будет аналогично сходимости по метрике).
Банаховы пространства [ править ]
Важную роль играют банаховы пространства (содержат перенос понятия полноты на случай нормированных пространств). Также банаховы пространства называют B-пространствами, далее в тексте обозначаются именно так.
Также в нормированных пространствах можно рассматривать ряды, понимая под рядом, например, предел частичных сумм. Другие методы суммирования также можно перенести на нормированные пространства (метод средних арифметических или метод Абеля).
Ряд из норм в нормированных пространствах — аналог ряда из модулей для понятия абсолютной сходимости.
В силу полноты пространства существует предел последовательности частичных сумм (так как последовательность частичных сумм сходится в себе). Заодно получаем оценку на норму суммы такого ряда:
Гильбертовы пространства [ править ]
Среди нормированных пространств выделяется подкласс так называемых гильбертовых пространств.
Неравенство Шварца [ править ]
Основное значение для скалярного произведения имеет неравенство Шварца:
Первые два свойства, очевидно, выполняются. Проверим, что этот функционал удовлетворяет неравенству треугольника:
Последний переход в неравенстве выполнен именно благодаря неравенству Шварца.
Доказанное неравенство треугольника превращает [math]H[/math] в нормированное пространство. Если оно является B-пространством, то его называют гильбертовым пространством.
Полнота евклидова пространства [ править ]
[math] \Longrightarrow [/math] :
Если последовательность сходится, то из неравенства [math]|x_j^ <(m)>— x_j| \le \|x^ <(m)>— x\|[/math] устанавливается, что последовательность сходится и покоординатно.
[math] \Longleftarrow [/math] :
Но по доказанному ранее утверждению из покоординатной сходимости следует сходимость по норме, что и требовалось доказать.
| Теорема (критерий компактности в [math] R^n [/math] ): |
| [math]\triangleleft[/math] |
Пространство последовательностей [ править ]
Второй классический пример гильбертовых пространств был предложен самим Гильбертом.
Далее, требуется проверить корректность алгебраических операций.
Требуемое следует из очевидно верного неравенства [math](a + b)^2 \le 2(a^2 + b^2)[/math] :
[math]\sum\limits_
Пространство Гильберта имеет важное понятие ортонормированной системы точек:
Из шара можно высверлить бесконечно много дырок одинакового радиуса( [math]R = \frac<\sqrt2> <10>[/math] ), и он не развалится.
КАРТИНОЧКА никому не нужна, вы ведь не хотите загреметь в сумасшедший дом из-за попытки представить высверливание дырок в бесконечномерном шаре? Вот и славненько.
Теорема Пифагора [ править ]
Теорема Пифагора получается предельным переходом равенства.
Применим теорему к ортогональному ряду из ОНС:
[math] \sum\limits_
[math] \sum\limits_
Возникает вопрос: всегда ли сходится описанный числовой ряд? Для ответа, как обычно, введем новые теоретические построения.
Теорема Бесселя [ править ]
Для некоторого набора коэффициентов [math] \beta_k [/math] рассмотрим скалярное произведение:
Нормированное векторное пространство
В нашем пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие:
Обобщение этих свойств на более абстрактные векторные пространства носит название нормы. Векторное пространство, в котором определена норма, называется нормированным пространством.
Содержание
Определение
Топологическая структура
Для любого полунормированного векторного пространства мы можем задать расстояние между двумя векторами 


Все нормы в конечномерном векторном пространстве эквивалентны с топологической точки зрения, так как они порождают одну и ту же топологию. А так как любое евклидово пространство полно, мы можем сделать вывод, что все конечномерные векторные пространства являются банаховыми пространствами. Нормированное векторное пространство V конечномерно тогда и только тогда, когда единичный шар 
Линейные отображения и двойственные пространства
Наиболее важными отображениями между двумя нормированными векторными пространствами являются непрерывные линейные отображения. Нормированные векторные пространства с такими отображениями образуют категорию.
Норма — это непрерывная функция в своём векторном пространстве. Все линейные отображения между конечномерными векторными пространствами также непрерывны.
Говоря о нормированных векторных пространствах мы должны упомянуть двойственные пространства. Двойственное пространство V‘ нормированного векторного пространства V — это пространство всех непрерывных линейных отображений из V на основное поле (поле комплексных или действительных чисел), а такие линейные отображения называются функционалами. Норма функционала 
Введение такой нормы превращает V‘ в нормированное векторное пространство. Важной теоремой о непрерывных линейных функционалах в нормированных векторных пространствах является теорема Хана — Банаха.
Нормированные пространства как фактор-пространства полунормированных пространств
является полунормой в векторном пространстве всех функций, интеграл Лебега от которых (справа) определён и конечен. Однако полунорма равна нулю для всех функций, носитель которых имеет нулевую меру Лебега. Эти функции образуют подпространство, которое мы «вычёркиваем», делая их эквивалентными нулевой функции.
Конечные произведения пространств
Для данных n полунормированных пространств Xi с полунормами pi мы можем определить произведение пространств как
с векторным сложением, определённым как
и скалярным умножением, определённым как
Определим новую функцию p
Линейное нормированное пространство
В евклидовом пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие:
Обобщение этих свойств на более абстрактные векторные пространства носит название нормы. Векторное пространство, в котором определена норма, называется нормированным векторным пространством (иногда просто нормированным пространством).
Содержание
Определение
Топологическая структура
Для любого полунормированного векторного пространства мы можем задать расстояние между двумя векторами 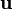
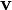
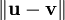
Все нормы в конечномерном векторном пространстве эквивалентны с топологической точки зрения, так как они порождают одну и ту же топологию. А так как любое евклидово пространство полно, мы можем сделать вывод, что все конечномерные векторные пространства являются банаховыми пространствами. Нормированное векторное пространство V конечномерно тогда и только тогда, когда единичный шар 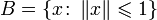
Линейные отображения и двойственные пространства
Наиболее важными отображениями между двумя нормированными векторными пространствами являются непрерывные линейные отображения. Нормированные векторные пространства с такими отображениями образуют категорию.
Норма — это непрерывная функция в своём векторном пространстве. Все линейные отображения между конечномерными векторными пространствами также непрерывны.
Говоря о нормированных векторных пространствах мы должны упомянуть двойственные пространства. Двойственное пространство V‘ нормированного векторного пространства V — это пространство всех непрерывных линейных отображений из V на основное поле (поле комплексных или действительных чисел), а такие линейные отображения называются функционалами. Норма функционала 
Введение такой нормы превращает V‘ в нормированное векторное пространство. Важной теоремой о непрерывных линейных функционалах в нормированных векторных пространствах является теорема Хана — Банаха.
Нормированные пространства как фактор-пространства полунормированных пространств
является полунормой в векторном пространстве всех функций, интеграл Лебега от которых (справа) определён и конечен. Однако полунорма равна нулю для всех функций, носитель которых имеет нулевую меру Лебега. Эти функции образуют подпространство, которое мы «вычёркиваем», делая их эквивалентными нулевой функции.
Конечные произведения пространств
Для данных n полунормированных пространств Xi с полунормами pi мы можем определить произведение пространств как
с векторным сложением, определённым как
и скалярным умножением, определённым как
Определим новую функцию p
Линейное нормированное пространство
В евклидовом пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие:
Обобщение этих свойств на более абстрактные векторные пространства носит название нормы. Векторное пространство, в котором определена норма, называется нормированным векторным пространством (иногда просто нормированным пространством).
Содержание
Определение
Топологическая структура
Для любого полунормированного векторного пространства мы можем задать расстояние между двумя векторами 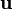
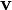
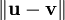
Все нормы в конечномерном векторном пространстве эквивалентны с топологической точки зрения, так как они порождают одну и ту же топологию. А так как любое евклидово пространство полно, мы можем сделать вывод, что все конечномерные векторные пространства являются банаховыми пространствами. Нормированное векторное пространство V конечномерно тогда и только тогда, когда единичный шар 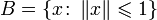
Линейные отображения и двойственные пространства
Наиболее важными отображениями между двумя нормированными векторными пространствами являются непрерывные линейные отображения. Нормированные векторные пространства с такими отображениями образуют категорию.
Норма — это непрерывная функция в своём векторном пространстве. Все линейные отображения между конечномерными векторными пространствами также непрерывны.
Говоря о нормированных векторных пространствах мы должны упомянуть двойственные пространства. Двойственное пространство V‘ нормированного векторного пространства V — это пространство всех непрерывных линейных отображений из V на основное поле (поле комплексных или действительных чисел), а такие линейные отображения называются функционалами. Норма функционала 
Введение такой нормы превращает V‘ в нормированное векторное пространство. Важной теоремой о непрерывных линейных функционалах в нормированных векторных пространствах является теорема Хана — Банаха.
Нормированные пространства как фактор-пространства полунормированных пространств
является полунормой в векторном пространстве всех функций, интеграл Лебега от которых (справа) определён и конечен. Однако полунорма равна нулю для всех функций, носитель которых имеет нулевую меру Лебега. Эти функции образуют подпространство, которое мы «вычёркиваем», делая их эквивалентными нулевой функции.
Конечные произведения пространств
Для данных n полунормированных пространств Xi с полунормами pi мы можем определить произведение пространств как
с векторным сложением, определённым как
и скалярным умножением, определённым как
Определим новую функцию p
Нормированное векторное пространство
В нашем пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие:
Обобщение этих свойств на более абстрактные векторные пространства носит название нормы. Векторное пространство, в котором определена норма, называется нормированным пространством.
Содержание
Определение
Топологическая структура
Для любого полунормированного векторного пространства мы можем задать расстояние между двумя векторами 


Все нормы в конечномерном векторном пространстве эквивалентны с топологической точки зрения, так как они порождают одну и ту же топологию. А так как любое евклидово пространство полно, мы можем сделать вывод, что все конечномерные векторные пространства являются банаховыми пространствами. Нормированное векторное пространство V конечномерно тогда и только тогда, когда единичный шар 
Линейные отображения и двойственные пространства
Наиболее важными отображениями между двумя нормированными векторными пространствами являются непрерывные линейные отображения. Нормированные векторные пространства с такими отображениями образуют категорию.
Норма — это непрерывная функция в своём векторном пространстве. Все линейные отображения между конечномерными векторными пространствами также непрерывны.
Говоря о нормированных векторных пространствах мы должны упомянуть двойственные пространства. Двойственное пространство V‘ нормированного векторного пространства V — это пространство всех непрерывных линейных отображений из V на основное поле (поле комплексных или действительных чисел), а такие линейные отображения называются функционалами. Норма функционала 
Введение такой нормы превращает V‘ в нормированное векторное пространство. Важной теоремой о непрерывных линейных функционалах в нормированных векторных пространствах является теорема Хана — Банаха.
Нормированные пространства как фактор-пространства полунормированных пространств
является полунормой в векторном пространстве всех функций, интеграл Лебега от которых (справа) определён и конечен. Однако полунорма равна нулю для всех функций, носитель которых имеет нулевую меру Лебега. Эти функции образуют подпространство, которое мы «вычёркиваем», делая их эквивалентными нулевой функции.
Конечные произведения пространств
Для данных n полунормированных пространств Xi с полунормами pi мы можем определить произведение пространств как
с векторным сложением, определённым как
и скалярным умножением, определённым как
Определим новую функцию p