Что такое нуль в математике
0 (число)
0 (ноль, нуль от лат. nullus — никакой) — целое число, разделяющее на числовой прямой положительные и отрицательные числа. Существуют два подхода к определению натуральных чисел — одни авторы причисляют нуль к натуральным числам, другие этого не делают. В российских школьных программах по математике не принято причислять нуль к натуральным числам, хотя это затрудняет некоторые формулировки (например, приходится различать деление с остатком и деление нацело).
Содержание
Основные свойства нуля
Применение
В математике
В физике
В других областях
Обобщения
Аналог нуля может существовать в любом множестве, на котором определена операция сложения; в высшей алгебре такой элемент называется нейтральным. Чаще всего используется вещественный нуль, то есть нуль в контексте множества вещественных чисел. Другие распространённые вариации:
История
Вавилонские математики использовали особый клинописный значок для шестидесятеричного нуля примерно начиная с 300 г. до н. э., а их учителя-шумеры, вероятно, сделали это ещё раньше.
Своеобразные коды нуля использовали ещё до нашей эры древние майя и их соседи в Центральной Америке (древние майя обозначали ноль стилизованным изображением ракушки).
В Древней Греции число 0 известно не было. В астрономических таблицах Клавдия Птолемея пустые клетки обозначались символом ο (буква омикрон, от др.-греч. ονδεν — ничего); не исключено, что это обозначение повлияло на появление нуля, однако большинство историков признаёт, что десятичный нуль изобрели индийские математики. Без нуля была бы невозможна открытая в Индии десятичная позиционная запись чисел. Первый код нуля обнаружен в индийской записи от 876 г., он имеет вид привычного нам кружочка.
В Европе долгое время нуль считался условным символом и не признавался числом; даже в XVII веке Валлис писал: «Нуль не есть число». В арифметических трудах отрицательное число истолковывалось как долг, а ноль — как ситуация полного разорения. Полному уравнению его в правах с другими числами особенно способствовали труды Леонарда Эйлера.
См. также
Ссылки
Полезное
Смотреть что такое «0 (число)» в других словарях:
число — Прие моч ное Источник: ГОСТ 111 90: Стекло листовое. Технические условия оригинал документа Смотри также родственные термины: 109. Число бетатронных колебаний … Словарь-справочник терминов нормативно-технической документации
Число зверя — … Википедия
Число Зверя — особое число, упоминаемое в Библии, под которым скрыто имя апокалиптического зверя; нумерологическое воплощение ставленника сатаны. Число зверя равно 666. Число 666 очень часто используемый элемент сатанинской атрибутики, наряду с перевёрнутым… … Википедия
Число дьявола — Число зверя особое число, упоминаемое в Библии, под которым скрыто имя апокалиптического зверя; нумерологическое воплощение ставленника сатаны. Число зверя равно 666. Число 666 очень часто используемый элемент сатанинской атрибутики, наряду с… … Википедия
число циклов — Полное количество отдельных выпусков (выбросов) ОТВ для данного устройства импульсного действия. Источник … Словарь-справочник терминов нормативно-технической документации
Число с плавающей запятой — Число с плавающей запятой форма представления действительных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную.… … Википедия
число — сущ., с., употр. очень часто Морфология: (нет) чего? числа, чему? числу, (вижу) что? число, чем? числом, о чём? о числе; мн. что? числа, (нет) чего? чисел, чему? числам, (вижу) что? числа, чем? числами, о чём? о числах математика 1. Числом… … Толковый словарь Дмитриева
Число Грэма — (Грехема, англ. Graham s number) большое число, которое является верхней границей для решения определённой проблемы в теории Рамсея. Названо в честь Рональда Грэма (англ.). Оно стало известно широкой публике после того, как Мартин … Википедия
ЧИСЛО — ЧИСЛО, числа, мн. числа, чисел, числам, ср. 1. Понятие, служащее выражением количества, то, при помощи чего производится счет предметов и явлений (мат.). Целое число. Дробное число. Именованное число. Простое число. (см. простой1 в 1 знач.).… … Толковый словарь Ушакова
Число 23 (фильм) — Роковое число 23 The Number 23 Жанр триллер/драма/детектив … Википедия
Число Ричардсона — ( ) критерий подобия в гидродинамике, равный отношению потенциальной энергии тела, погружённого в жидкость к его кинетической энергии. Под «телом» здесь обычно понимается рассматриваемая жидкость или газ. В общем случае число Ричардсона… … Википедия
Математика с нуля: чем интересно число 0?
Попробуем делить на ноль и узнаем больше об истории и свойствах числа, расположенного ровно посередине числовой оси.
Ноль — это, пожалуй, первое в нашей жизни загадочное число. Мы много слышали, например, о чудесах числа Пи, но мало кто имеет с ним дело в повседневной жизни. Не говоря уже о комплексных числах. А вот с нолём мы сталкиваемся повсюду: даже на клавиатуре обозначающая его цифра завершает ряд.
Но любой понимает, что с этим числом не всё в порядке. В детстве, когда мы ещё думали, что арифметика нужна только для счёта, нам объясняли, что ноль — это отсутствие. И это было странно.
Читайте также :
Поэтому и в истории человечества это число появилось поздно. Торговцы активно использовали счёт, но продавать, например, «ноль овец» не имело смысла. Впрочем, как и отрицательное их количество.
Вышло любопытно: например, древние греки не использовали ноль в принципе, зато уже знали об иррациональных числах, таких как √2. Это было связано с их любовью к геометрии: если у прямоугольного треугольника стороны будут равны 1, длина гипотенузы вычисляется как √2.
Но как же десятеричная система счёта? Ведь даже чтобы записать «10», нам нужен ноль. Но здесь дело только в записи числа: если вы вспомните римские цифры, то поймёте, что десятку можно представить и как Х. Конечно, такая форма была не особенно удобной, но даже вавилоняне, пользовавшиеся позиционной системой счисления (то есть, близкой нашей, а не древнеримской), долго обходились без ноля. Некоторое время его просто не было: числа, скажем, 36 и 306 не различались по написанию и определялись по контексту. Потом его роль стали выполнять два клинышка, вроде вот этих: 3’’6. Но и тогда они самостоятельной роли не играли — не было числа «ноль».
Сложно сказать, когда оно в действительности появилось. При этом есть свидетельства, что в Индии его использовали еще до нашей эры, после чего его переняли арабы — а вот на Западе оно стало входить в практику только в XIII веке усилиями итальянского математика Леонарда Фибоначчи. И то, его любовь к арабскому счислению долго не воспринималась всерьёз.
Известно, что первые слова, обозначавшие количество, имели конкретное применение — «пять лошадей» и «пять лодок» были для древнего человека разными категориями. Чтобы изобрести ноль, требовалось перейти на новый уровень абстрактного мышления.
Но если мы поверим в ноль, его свойства поразят воображение.
Возвести в нулевую степень
Ещё по этой теме :
С самыми простыми операциями проблем не возникает: прибавить ноль или вычесть его из числа — число остаётся тем же, умножить на ноль — получится ноль… Всё это укладывается в рамки здравого смысла. Сложнее становится при возведении в нулевую степень. В школе сообщают, что результатом в каждом случае будет единица. Откуда она взялась?
Тут рассудок уже пасует. Степень — это, как известно, то, сколько раз мы берём число как множитель самого себя.
Если степень нулевая, число не является множителем ни разу, но… как из этой пустоты «родилась» единица?
Чаще всего в школе этот вопрос решается догматически: на объяснения не остаётся желания и сил. А ведь именно здесь пролегает одна из границ, за которой простая арифметика, наглядно показываемая на яблоках и прочих исчислимых вещах, становится уже чистой и прекрасной абстракцией.
Вспомним правила обращения с числами, возводимыми в степень, и представим себе следующий пример:
В отношениях с одинаковыми основаниями степеней мы можем делать следующее:
Так вот чудесным образом, благодаря только принятию ноля как числа, мы переходим к новому странному открытию, и математика совершает куда более далёкий прыжок от реальности, чем просто представление «у меня ноль конфет».
Но именно внутренняя логика системы, которая может быть понята умом, но не может быть представлена в вещественном мире — это и есть красота абстракции.
Поделить на ноль
Это может быть интересно :
«Деление на ноль» давно стало интернет-мемом, правда, довольно неопределённым. То оно означает аннигиляцию чего бы то ни было (а ведь логичнее было бы умножить на ноль), то вовсе разрушение математических основ мироздания. И второе ближе к истине.
Большинство учёных всё-таки считают эту операцию с нолём невозможной или обладающей неопределённым результатом.
В чём же дело, и почему даже машины не могут между собой «договориться»?
Чисто арифметически делимость на ноль приводит к рискованным выводам. Смотрите сами:
Это лишь известное нам свойство ноля. Но если на него можно делить, то, сократив обе части, мы получим:
Почему же речь иногда заходит о бесконечности? Дело в том, что проблему пытаются решить через деление на бесконечно малую функцию, то есть построение графика функции, где x стремился бы к нулю. Так мы пытаемся найти y = 1 / x, и получается следующее:
Кстати говоря, с делением ноля на ноль наблюдается ещё большее единодушие: тут, если мы соберёмся построить функцию, результаты могут быть практически какими угодно (0, ±1, ±∞…) В общем, ноль, оставаясь числом, снова подрывает основы математики, если мы нарушаем неприкосновенность его свойств.
Ноль — чётное число?
Это может быть интересно :
Если он так необычен (и не забываем, что он не является ни положительным, ни отрицательным), можно ли говорить о его чётности? Интуитивно мы догадываемся, что он чётный, ведь целые числа сменяют друг друга именно по такому принципу: 2 — чётное, 1 — нечётное, следующим должно быть снова чётное. Но странность ноля настораживает, подсказывает, что и в этом вопросе нужно держать ухо востро.
Какое главное требование он должен пройти в этом случае? Деление на двойку без остатка, и он выдерживает испытание с достоинством: 0/2=0. Получается целое число 0, причём сколько бы мы ни продолжали деление, результат будет получаться одинаковым — можно сказать, что он является «наиболее» чётным или «бесконечно» чётным числом.
Если быть более точным, мы должны взять другое определение с обратной операцией. Чётное число может быть представлено в виде 2x, где x — целое число, но и в таком случае всё просто: 0 = 2 ∙ 0.
Есть и такое свойство чётных чисел, что при сложении двух из них должно получаться снова чётное, проверим:
При всей необычности ноля даже его удивительное соответствие всем критериям кажется странным, не так ли?
Что смотреть и читать о ноле?
Чтобы узнать больше о ноле как одном из самых загадочных явлений математики, а также об истории его «открытия», вы можете обратиться к следующим ресурсам:
1. Numberphile. Это популярнейший в среде любителей математики Youtube-канал, у которого уже более чем 1,5 миллиона подписчиков. Есть видео и о ноле, которые в переводе на русский можно найти здесь.
2. Книга Чарльза Сейфе «Ноль. Биография опасной идеи». Автор, хоть и не без излишнего сгущения красок, рассказывает об истории ноля как числа и цифры — причем в обширном контексте истории науки, от Архимеда до теории струн. В качестве бонуса вы получите приложения с задачками, где используется ноль. Например, вам предложат доказать, что Уинстон Черчилль был морковкой, и построить машину времени из кротовой норы.
3. Сборник эссе, в которых фантаст Айзек Азимов рассказывает о том, как человек, переходя от счёта на пальцах ко всё более сложным вычислениям, разработал основные математические операции, а также о том, как числа связаны с нашим восприятием времени и пространства. Природе ноля и его парадоксам посвящена открывающая книгу статья «Nothing Counts».
Даже если вам не нравились в школе ни арифметика, ни алгебра, у вас всегда есть возможность ими заинтересоваться. Учить математику с нуля уже не получится — худо-бедно мы начали считать ещё дошколятами. А вот полюбить её с нуля — вполне реальная перспектива.
Что означает число ноль
Откуда взялась «пустая» цифра?
История появления нуля скрыта множеством тайн и загадок. Исследователи полагают, что эта цифра вводилась древними математиками разных эпох и цивилизаций. Но, не осознавая всю ее важность, ученые отказывались от нее. По данным историков ноль был известен еще в Вавилоне в 1700-1000 гг. до н.э., хотя более точной считается информация, что ноль придумали индийские математики за 600 лет до н.э. В Европе же удобная система арабских чисел с нулем появилась лишь в XIII веке, где ранее любые числа, вплоть до сотен и тысяч, обозначались громоздким набором латинских букв.
Эзотерический символизм нуля
Изучение древних трактатов, а также аналитических размышлений Е. П. Блаватской приводит к тому, что ноль нельзя понимать просто, как математическую цифру. Древние ассоциировали его с первозданной пустотой, не имеющей параметров, границ и величины – поистине идеальный параметр для описания абстрактных пространств, к чему впоследствии пришли математики XVII-XVIII веков. В ноль вкладывается принцип зарождения любых вещей, из чего идет мысль, что эта цифра возникла не для определения многократности других цифр, а наоборот, сама породила их. Ноль – это всеобъемлющая пустота, которая принимает форму величины лишь, следуя за какой-то цифрой, показывающей мощь этой «не-цифры».
Ноль в математике и физике
Хотя физика с математикой тесно связаны, понятие нуля здесь весьма четко разграничено, и практически не имеет точек соприкосновения. В физике ноль является точкой отсчета, главным образом, определяющей пространство какого-либо реально существующего параметра, примером чего является температурная шкала. Однако современные физики, изучающие теорию струн, астрофизику и глубинные принципы теории относительности, приходят к понятиям сингулярности и узлов Вселенной, где ноль является принципиально важным параметром.
В математике же ноль – это не просто начало многомерных декартовых, сферических, полярных и других систем координат, это уход в пространство отрицательных чисел, которые не способны характеризовать физические явления. Более того, парадоксы, связанные с невозможностью деления любых чисел на ноль, определяются, как методы исследования абстрактных множеств. В математическом анализе деление на ноль – это не табу, это бесконечность, которая может быть преобразована теорией пределов и описана различными Фурье-образами. Однако деление нуля самого на себя, как и деление бесконечностей – это все еще неопределенность.
Правильно «нОль» или «нУль»?
Сейчас принято говорить и «ноль» и «нуль», хотя в учебниках математики чаще встречается именно «нуль». Это связано с латинским термином «nullus», обозначающим «никакой». Между тем, интересно, что индийцы для описания этой цифры использовали слово «свободный», а вовсе не «никакой» или «пустой», что может стать незаурядным поводом к философским размышлениям.
Нулевое число (0)
Определение нулевого числа
Когда на столе 2 яблока и мы берем 2 яблока, мы можем сказать, что на столе нет яблок.
Нулевое число не является положительным и отрицательным числом.
Ноль также является цифрой-заполнителем в других числах (например: 40,103, 170).
Нулевая цифра
При написании чисел нулевая цифра используется в качестве заполнителя.
204 = 2 × 100 + 0 × 10 + 4 × 1
История нулевых номеров
Кто придумал нулевое число?
Современный символ 0 был изобретен в Индии в VI веке, позже использовался персами и арабами, а затем и в Европе.
Символ нуля
В арабской системе счисления используется символ ٠.
Свойства с нулевым числом
x представляет любое число.
| Операция | Правило | пример |
|---|---|---|
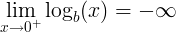 | ||
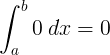 |
Нулевое дополнение
Сложение числа плюс ноль равно числу:
Нулевое вычитание
Вычитание числа минус ноль равно числу:
Умножение на ноль
Умножение числа на ноль равно нулю:
Число деленное на ноль
Деление числа на ноль не определено:
x ÷ 0 не определено
5 ÷ 0 не определено
Ноль делится на число
Деление нуля на число равно нулю:
Число в нулевой степени
Степень числа, возведенного в ноль, равна единице:
Логарифм нуля
Логарифм нуля по основанию b не определен:
Нет числа, с которым мы могли бы поднять основание b до нуля.
Только предел логарифма x по основанию b, когда x сходится к нулю, равен минус бесконечности:
Наборы, содержащие ноль
| Установить | Установить обозначение членства |
|---|---|
| Натуральные числа (неотрицательные) | 0 ∈ ℕ 0 |
| Целые числа | 0 ∈ ℤ |
| Вещественные числа | 0 ∈ ℝ |
| Сложные числа | 0 ∈ ℂ |
| Рациональное число | 0 ∈ ℚ |
Набор четных чисел:
Набор нечетных чисел:
Ноль является членом набора четных чисел:
Есть два определения набора натуральных чисел.
Набор неотрицательных целых чисел:
Набор натуральных чисел:
Ноль является членом набора неотрицательных целых чисел:
Ноль не входит в набор натуральных чисел:
У целых чисел есть три определения:
Набор неотрицательных целых чисел:
Набор натуральных чисел:
Ноль является членом набора целых чисел и набора неотрицательных целых чисел:
Ноль не входит в набор натуральных чисел:
Ноль входит в набор целых чисел:
Является ли ноль рациональным числом?
Ноль можно записать как частное двух целых чисел.
Положительное число определяется как число больше нуля:
Поскольку ноль не больше нуля, это не положительное число.
Число 0 не является простым числом.
Ноль не является положительным числом и имеет бесконечное количество делителей.
Ноль или нуль — как правильно?
В век интернета кажется, что нет никакой разницы, как писать — «ноль» или «нуль». Главное, чтобы суть текста была ясна. Но вы удивитесь, если узнаете, что «ноль» и «нуль» — это разные слова. Иногда мы слышим: «моя бабушка в деревне говорила нуль» — «это неправильно! Надо говорить — ноль». Верно ли это? Ноль или нуль — вот в чем вопрос.
Если мы заглянем в толковый словарь, который стоит на полке у нас дома, то увидим следующие определения, как для слова «ноль», так и для слова «нуль»:
Сейчас решение «ноль» или «нуль» принимается в зависимости от ситуации, мы постараемся рассказать, как не ошибиться в употреблении этих похожих по звучанию, но иногда непохожих по значению, слов.
Происхождение слов «ноль» и «нуль»
Слово «нуль» ввел в русский язык Петр I. В кириллической системе исчисление велось с единицы. Древнерусские математики называль «ноль» — «оном» или «ничто». У слова «ноль» шведские и немецкие корни. Из немецкого языка к нам попал «нуль» (“null”), а из шведского — «ноль» (“noll”). Впрочем, у обоих вариантов общий предок. Они произошли от лат. “nullus” – «ничто».
Когда пишется «нуль»
Слово «нуль» уже давно начало сдавать свои позиции и постепенно устаревало. В современной речи оно кажется вычурным и используется, чтобы подчеркнуть значимость слова, сделать его более экспрессивным. Органично оно смотрится примерно в таких текстах:
Но, если хорошо подумать, «нуль» мы и так употребляем достаточно часто:
Поэтому слово «нуль» можно назвать устаревшим лишь в определенном контексте. Мы до сих пор употребляем его в некоторых устойчивых выражениях, и это — не грамматическая ошибка.
Язык — живой организм, который постоянно развивается. Какие-то слова уходят из оборота, какие-то приходят. Не всегда лингвистические нормы успевают подкрепляться правилами. Иногда на помощь людям приходит то, что называют «лингвистическим чутьем». Количество чтения нередко переходит в качество письма. Есть те, кто всегда употребляет «нуль» правильно, потому что «С вас нуль рублей и три копейки» — неблагозвучное предложение.
Когда пишется «ноль»
Ноль — это современный «нуль». У него есть сразу несколько значений:
Логично, что его мы используем чаще.
Ноль или нуль: возможны оба варианта
Теперь мы знаем, что правильность выбора «ноль» или «нуль» зависит от контекста фразы и от эпохи. Если вы пишете исторический роман, логично будет использовать «нуль», если речь идет о математическом примере — «ноль». Возможно, однажды «нуль» покинет русский язык, как и многие слова, которые устарели и ушли из языка за ненадобностью.
Какое из этих слов «важнее» в языке — неправильная постановка вопроса. Они совершенно равноправны и пока оба употребляются в тех или иных ситуациях. В свободном употреблении, в обычной разговорной речи, ошибиться не так страшно. Кроме того, иногда это придает фразе экспрессии и окрашивает нужными эмоциями.









