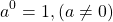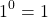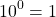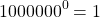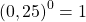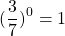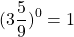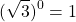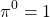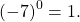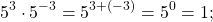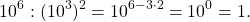Что такое нулевая степень
Степень 0
В алгебре возведение с нулевую степень встречается часто. Что такое степень 0? Какие числа можно возводить в нулевую степень, а какие — нет?
Любое число в нулевой степени, за исключением нуля, равно единице:
Таким образом, какое бы число ни возвели в степень 0, результат всегда получится одинаковый — единица.
И 1 в степени 0, и 2 в степени 0, и любое другое число — целое, дробное, положительное, отрицательное, рациональное, иррациональное — при возведении в нулевую степень дает единицу.
Единственное исключение — нуль.
Нуль в нулевой степени не определен, такое выражение не имеет смысла.
То есть в нулевую степень можно возводить любое число, кроме нуля.
Если при упрощении выражения со степенями получается число в нулевой степени, его можно заменить единицей:
Если при упрощении получается переменная или выражение с переменными в нулевой степени, пишем дополнительное условие — основание степени должно быть отличным от нуля:
Число в нулевой степени
Возведение в степень является одним из основных математических действий, без которых невозможны сложные расчеты. При этом отдельного рассмотрения заслуживает нулевая степень числа.
Возведение числа в нулевую степень
Известно, что при x 0 любое x равно 1 (x 0 = 1). Чтобы доказать это, нужно выяснить, откуда собственно взялся этот ноль?
Для этого вспомним формулы сложения и вычитания степеней.
7 3 = 7 2+1 = 7 2 × 7 1 = 7 × 7 × 7, ⇒
7 0 = 7 3-3 = 7 3 ÷ 7 3 = 1
Доказательство получено. Однако есть исключение из этого правила.
Парадокс нуля
Здесь все гораздо сложнее, но не настолько, чтобы не разобраться.
Известно, что 0 x = 0. Например: 0 4 = 0 × 0 × 0 × 0 = 0
Почему же мы часто встречаем выражение 0 0 = 1?
Подберем значения по табл.1.
Таблица 1. Функция ƒ(x) = x x
| x | x x |
| 1 | 1 |
| 0,9 | 0,909 |
| 0,8 | 0,836 |
| 0,7 | 0,779 |
| 0,6 | 0,736 |
| 0,5 | 0,707 |
| 0,4 | 0,693 |
| 0,3 | 0,697 |
| 0,2 | 0,725 |
| 0,1 | 0,794 |
| 0,01 | 0,955 |
| 0,001 | 0,993 |
Как видим, с определенного момента значение x x растет вместе с уменьшением x. В этом нет ничего сверхъестественного, это всего лишь пример действия формулы
Изобразим это на графике

Таким образом, делаем предположение, что это выражение является пределом.
Выразить это можно так:
Проверим, вычислив это значение.
Преобразуем основание выражения. Получаем:
x x = (e ln x ) x = e x ln x
Получаем следующее выражение:
Пользуемся правилом Лопиталя:
Официальная позиция современной математики гласит, что выражение 0 0 — представляет собой неопределенность, то есть не имеет точного значения.
Однако на практике, при расчетах, его значение подстраивается под конкретные требования. И чаще всего в этих случаях оно равно единице. Чтобы лучше разобраться с темой нулевой степени, советуем посмотреть видео ниже.
Ноль в степени ноль
Ноль — наверное самое загадочное число и самое контринтуитивное. Ведь его аналога в реальной жизни просто нет. Ноль — это отсутствие чего-то. Но почему ноль в степени ноль равняется единице? И главный вопрос, так ли это на самом деле? Можете проверить на своем калькуляторе до того, как прочтете…
Ноль «в степени» ноль
Как такое может быть? А вот как: 1 0 =1, 2 0 =1…. х 0 =1. Любое число при взведении в нулевую степени равняется единице. Чем сам ноль хуже? Но не все так просто. 
Что означает возвести в степень? Например «два в квадрате». Что мы делаем, мы двойку умножаем на саму себя 2 раза (2*2=4), «два в кубе», двойку умножаем саму на себя 3 раза (2*2*2=8). А что если степень, это «ноль»? Нужно взять число и умножить само на себя…. ноль раз? Это странно.
Вот как выглядит график функции y=x x
Видно, что при уменьшении значения Х значение У сначала снижается, а потом начинает расти и превращается… в единицу при условии очень маленьких (почти нулевых) значениях Х. Было бы логично предположить, что когда значение уменьшится до ноля, там тоже будет единица.
Еще раз, вернемся к простым цифрам:
Что означает эта запись? Чтобы получить девять, нужно тройку умножить два раза. Правда же?
Сколько раз нужно умножить тройку саму на себя, чтобы получить единицу? А если разделить 1 на 3? Простого ответа нет? Логично, что чем больше значение степени, тем больше результат, и чем меньше это значение, тем и результат меньше.
Но на графике выше показано, что кривая «упирается» в предел, в единицу. Точнее, значение функции становится равным 1, когда ноль еще даже не достигнут. И если уменьшать Х еще больше, все равно, дальше единицы не сдвинуться.
Контекст
Как получается, что при умножении ноля самого на себя получается что-то большее самого ноля?
Если мы в реальной жизни (а не в математике) съели все яблоки и их у нас 0, то сколько бы мы не умножали отсутствующие яблоки на такие же «нулевые» фрукты, как может у нас возникнуть целое яблоко? Если вам кажется такой вопрос простым, так и есть.
С одной точки зрения это странное выражение будет равняться единице, а вот с другой оно будет «не определено». То есть никакой единицы а результате умножения ноля на ноль и быть не может, да?
Математика говорит, что:
3 2 ×3 2 это тоже самое, что и 3 2+2 = 3 4 = 3 × 3 × 3 × 3= 81
4 5 ÷4 3 это тоже самое, что и 4 5–3 = 4 2 = 4 × 4 = 16
Тогда, если степени одинаковы:
3 2 ÷3 2 это тоже самое, что и 3 2-2 = 3 0 = Ой?!
Но ведь мы можем и не вычитать степени, а просто сделать две операции отдельно:
3 2 ÷3 2 это тоже самое, что и 3 2-2 = 3 0 , но 3 2 =9, тогда 3 2 ÷3 2 = 3 2-2 или 3 2 ÷3 2 =9÷9=1
А что будет если одно число поделить на самого себя? Единица!
Матанализ
С точки зрения математического анализа, все одновременно и сложно, и совсем просто. Ноль в степени ноль = неопределенность. Что, согласитесь, более логично. Ведь если у нас нет ничего и мы ничего умножим само на себя, не может же возникнуть что-то из этой пустоты?
Теория множеств
Давайте посмотрим с точки зрения теории множеств. Допустим, у нас есть два множества.
Первое множество, это количество символов пароля, которым закрыт доступ к вашей страничке в соцсети, или, еще лучше, PIN код банковской карты допустим — 4 символа.
Второе множество, это количество значений, корыте может принимать каждый символ. Предположим, что это только цифры, значит цифр — 10.
Вопрос, сколько вариантов комбинаций существует? Сколько раз нужно ввести случайную комбинацию, чтобы угадать пароль? Каждый символ:
10 4 =10 000 тысяч вариантов.
Можно сказать, что множество цифр (10) отображается на множестве возможных символов (4). Но есть и «пустые» множества. Например, вы не поставили пароль вовсе, у вас ноль символов, которые можно угадать, так сколько попыток понадобится, чтобы получить доступ к счету? Ровно одна.
То есть при 10 0 =1, но тоже самое случится, если пароля нет и значений тоже нет 0 0 =1. Простыми словами, ноль в степени ноль, означает, что пароль не установлен и каждое значение тоже 0. Тогда может существовать только одна такая «комбинация».
А на самом деле?
Практического применения это математическое выражение, как нетрудно догадаться, не имеет вовсе. Ни одном инженеру, ни одному экономисту не придет в голову умножать ноль на ноль ноль раз. Это просто не применимая конструкция. Так что вопрос остается в области математики, и может быть философии.
Это наверное единственный случай, когда оставаясь математиком можно для свободно для себя решать чему равно «0 в степени 0».