Что такое нулевое сопротивление в физике

Закон Ома

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Сопротивление

Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.

Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.

Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.

Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.

Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала.

Эту закономерность можно описать следующей формулой:

Сопротивление

R = ρ l/S

R — сопротивление [Ом]

l — длина проводника [м]

S — площадь поперечного сечения [мм^2]

ρ — удельное сопротивление [Ом*мм^2/м]

Единица измерения сопротивления — Ом. Названа в честь физика Георга Ома.

Площадь поперечного сечения проводника и удельное сопротивление содержат в своих единицах измерения мм^2. В таблице удельное сопротивление всегда дается в такой размерности, да и тонкий проводник проще измерять в мм^2. При умножении мм^2 сокращаются и мы получаем величину в СИ.

Но это не отменяет того, что каждую задачу нужно проверять на то, что там мм^2 в обеих величинах! Если это не так, то нужно свести не соответствующую величину к мм^2.

Таблица удельных сопротивлений различных материалов

Константан ( сплав Ni-Cu + Mn)

Нейзильбер (сплав меди цинка и никеля)

Никелин ( сплав меди и никеля)

Нихром ( сплав никеля хрома железы и марганца)

Резистор

Все реальные проводники имеют сопротивление, но его стараются сделать незначительным. В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.

Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.

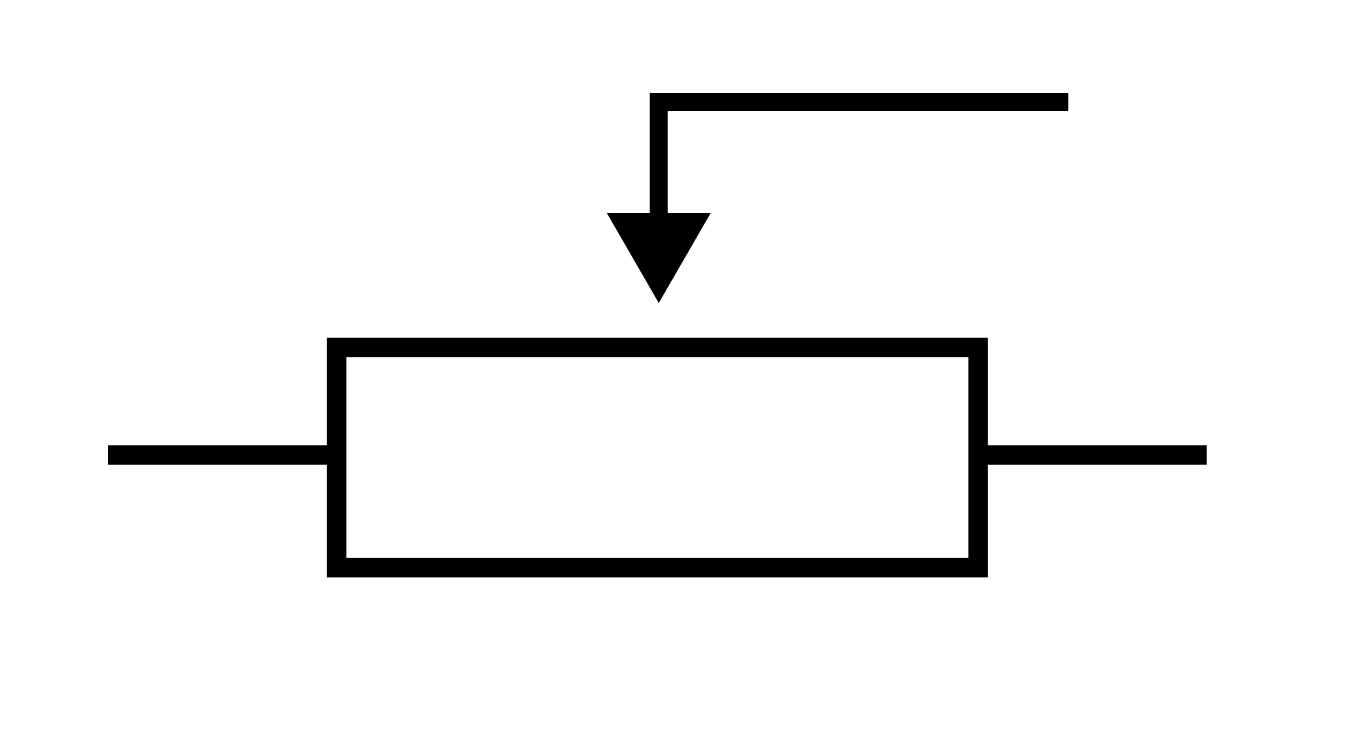
Вот так резистор изображается на схемах:

В школьном курсе физики используют Европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.

Вот так резистор выглядит в естественной среде обитания:

Полосочки на нем показывают его сопротивление.

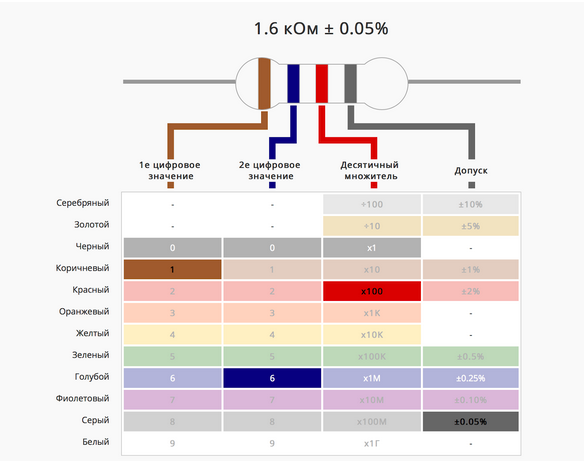
На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:

О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.

Реостат

Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат.

Стрелка сверху — это ползунок. По сути, он отсекает ту часть резистора, которая находится от него справа. То есть, если мы двигаем ползунок вправо — мы увеличиваем длину резистора, а значит и сопротивление. И наоборот — двигаем влево и уменьшаем.

По формуле сопротивления это очень хорошо видно, так как длина проводника находится в числителе:

Сопротивление

R = ρ l/S

R — сопротивление [Ом]

l — длина проводника [м]

S — площадь поперечного сечения [мм^2]

ρ — удельное сопротивление [Ом*мм^2/м]

Закон Ома для участка цепи

С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.

Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. Эти реакции выделяют энергию, которая потом передается электрической цепи.

У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «-».

У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.

Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.

Математически его можно описать вот так:

Закон Ома для участка цепи

I = U/R

R — сопротивление [Ом]

Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.

Сила тока измеряется в Амперах, а подробнее о ней вы можете прочитать в нашей статье 😇

Давайте решим несколько задач на Закон Ома для участка цепи.

Задача раз

Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом.

Решение:

Возьмем закон Ома для участка цепи:

Ответ: сила тока, проходящего через лампочку, равна 0,25 А

Давайте усложним задачу. И найдем силу тока, знаю все параметры для вычисления сопротивления и напряжение.

Задача два

Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а длина нити накаливания равна 0,5 м, площадь поперечного сечения 0,01 мм^2, а удельное сопротивление нити равно 1,05 Ом*мм^2/м.

Решение:

Сначала найдем сопротивление проводника.

Площадь дана в мм^2, а удельное сопротивления тоже содержит мм^2 в размерности.

Это значит, что можно подставлять значения без перевода в СИ:

R = 1,05*0,5/0,01 = 52,5 Ом

Теперь возьмем закон Ома для участка цепи:

Ответ: сила тока, проходящего через лампочку, приблизительно равна 4,2 А

А теперь совсем усложним! Определим материал, из которого изготовлена нить накаливания.

Задача три

Из какого материала изготовлена нить накаливания лампочки, если настольная лампа включена в сеть напряжением 220 В, длина нити равна 0,5 м, площадь ее поперечного сечения равна 0,01 мм^2, а сила тока в цепи — 8,8 А

Решение:

Возьмем закон Ома для участка цепи и выразим из него сопротивление:

Подставим значения и найдем сопротивление нити:

Теперь возьмем формулу сопротивления и выразим из нее удельное сопротивление материала:

Подставим значения и получим:

ρ = 25*0,01/0,5 = 0,5 Ом*мм^2/м

Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.

Таблица удельных сопротивлений различных материалов

Константан ( сплав Ni-Cu + Mn)

Нейзильбер (сплав меди цинка и никеля)

Никелин ( сплав меди и никеля)

Нихром ( сплав никеля хрома железы и марганца)

Ответ: нить накаливания сделана из константана.

Закон Ома для полной цепи

Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.

В таком случае вводится Закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.

Так, стоп. Слишком много незнакомых слов — разбираемся по-порядку.

Что такое ЭДС и откуда она берется

ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.

Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.

Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.

В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:

Закон Ома для полной цепи

I = ε/(R + r)

R — сопротивление [Ом]

r — внутреннее сопротивление источника [Ом]

Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.

Решим задачу на полную цепь.

Задачка

Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом

Решение:

Возьмем закон Ома для полной цепи:

Ответ: сила тока в цепи равна 1 А.

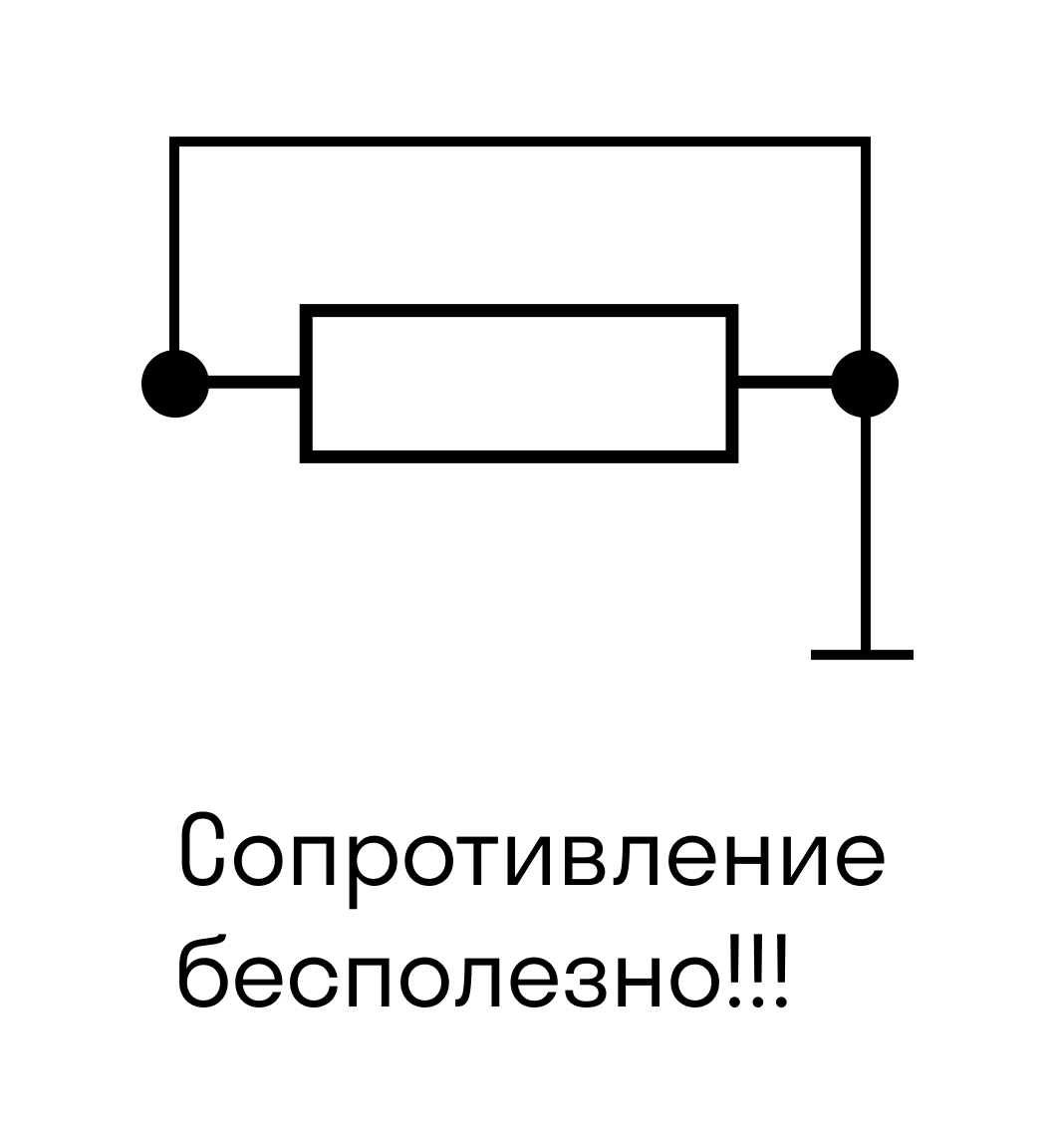
Когда «сопротивление бесполезно»

Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.

А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.

Ток идет по пути наименьшего сопротивления.

Теперь давайте посмотрим на закон Ома для участка цепи еще раз.

Закон Ома для участка цепи

I = U/R

R — сопротивление [Ом]

Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.

Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.

Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.

Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.

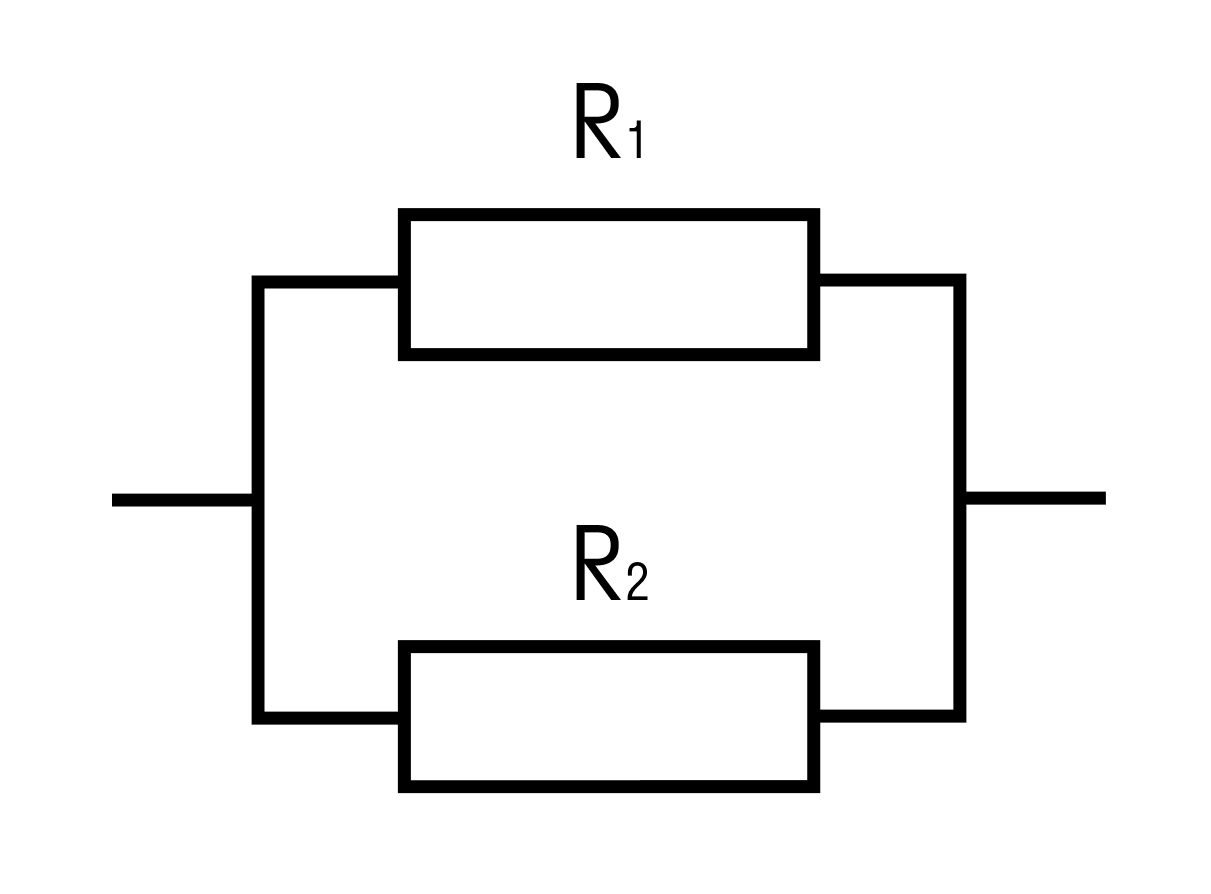
Параллельное и последовательное соединение

Все это время речь шла о цепях с одним резистором. Рассмотрим, что происходит, если их больше.

Резисторы следуют друг за другом

Между резисторами есть два узла

Узел — это соединение трех и более проводников

Сила тока одинакова на всех резисторах

Сила тока, входящего в узел, равна сумме сил токов, выходящих из него

Общее напряжение цепи складывается из напряжений на каждом резисторе

Напряжение одинаково на всех резисторах

Общее сопротивление цепи складывается из сопротивлений каждого резистора

Общее сопротивление для бесконечного количества параллельно соединенных резисторов

1/R = 1/R1 + 1/R2 + … + 1/Rn

Общее сопротивление для двух параллельно соединенных резисторов

Общее сопротивление бесконечного количества параллельно соединенных одинаковых резисторов

Зачем нужны эти соединения, если можно сразу взять резистор нужного номинала?

Начнем с того, что все электронные компоненты изготавливаются по ГОСТу. То есть есть определенные значения резисторов, от которых нельзя отойти при производстве. Это значит, что не всегда есть резистор нужного номинала и его нужно соорудить из других резисторов.

Параллельное соединение также используют, как «запасной аэродром»: когда на конечный результат общее сопротивление сильно не повлияет, но в случае отказа одного из резисторов, будет работать другой.

Признаемся честно: схемы, которые обычно дают в задачах (миллион параллельно соединенных резисторов, к ним еще последовательный, а к этому последовательному еще миллион параллельных) — в жизни не встречаются. Но навык расчета таких схем впоследствии упрощает подсчет схем реальных, потому что так вы невооруженным глазом отличаете последовательное соединение от параллельного.

Решим несколько задач на последовательное и параллельное соединение.

Задачка раз

Найти общее сопротивление цепи.

R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом, R4 = 4 Ом.

Решение:

Общее сопротивление при последовательном соединении рассчитывается по формуле:

R = R1 + R2 + R3 + R4 = 1 + 2 + 3 + 4 = 10 Ом

Ответ: общее сопротивление цепи равно 10 Ом

Задачка два

Найти общее сопротивление цепи.

Решение:

Общее сопротивление при параллельном соединении рассчитывается по формуле:

R = (R1 * R2)/R1 + R2 = 4*2/4+2 = 4/3 = 1 ⅓ Ом

Ответ: общее сопротивление цепи равно 1 ⅓ Ом

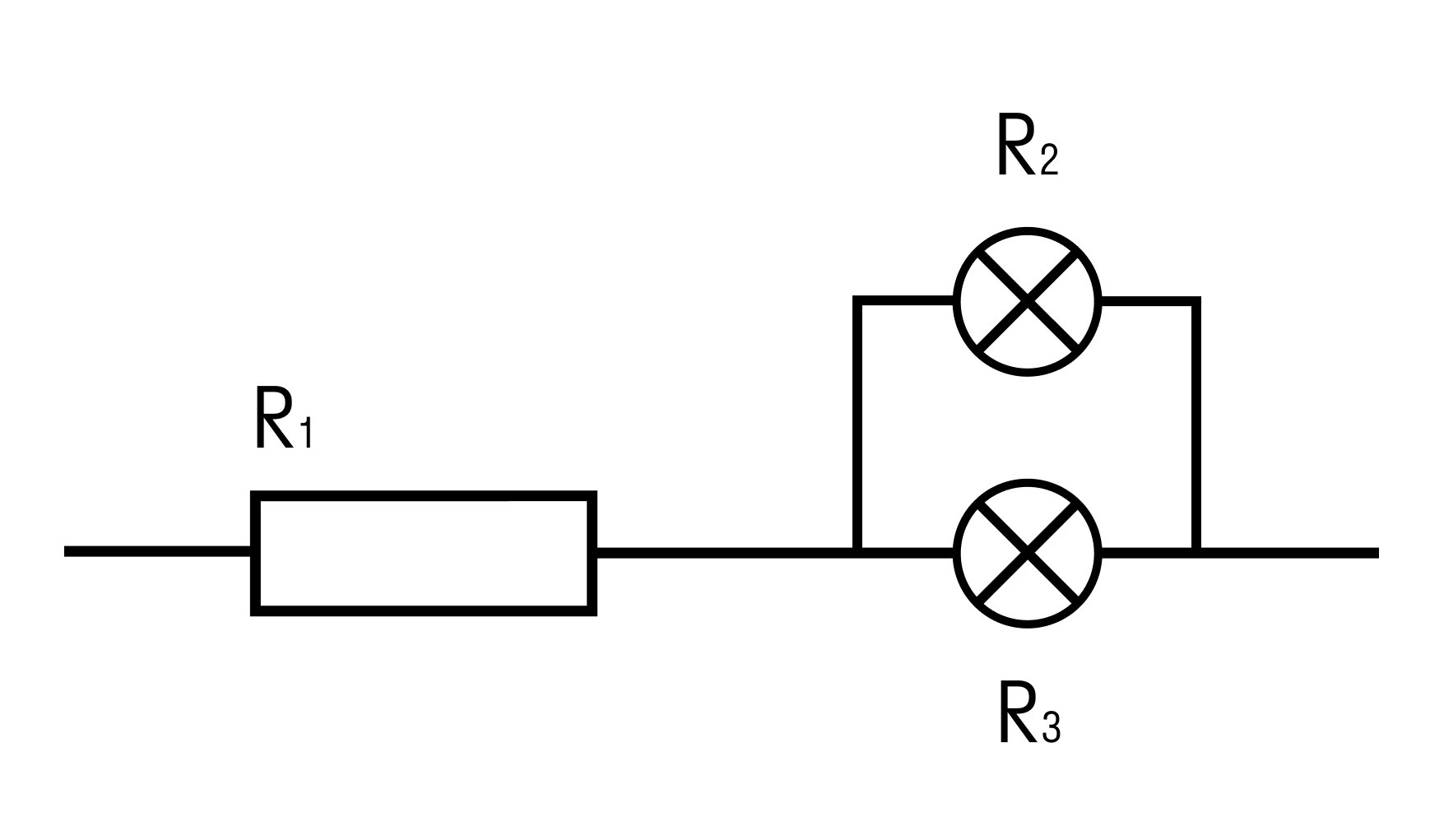
Задачка три

Найти общее сопротивление цепи, состоящей из резистора и двух ламп.

R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом

Решение:

Сначала обозначим, что лампы с точки зрения элемента электрической цепи не отличаются от резисторов. То есть у них тоже есть сопротивление, и они также влияют на цепь.

В данном случае соединение является смешанным. Лампы соеденены параллельно, а последовательно к ним подключен резистор.

Сначала посчитаем общее сопротивление для ламп. Общее сопротивление при параллельном соединении рассчитывается по формуле:

Rламп = (R2 * R3)/R2 + R3 = 2*3/2+3 = 6/5 = 1,2 Ом

Общее сопротивление при последовательном соединении рассчитывается по формуле:

R = R1 + Rламп = 1 + 1,2 = 2,2 Ом

Ответ: общее сопротивление цепи равно 2,2 Ом.

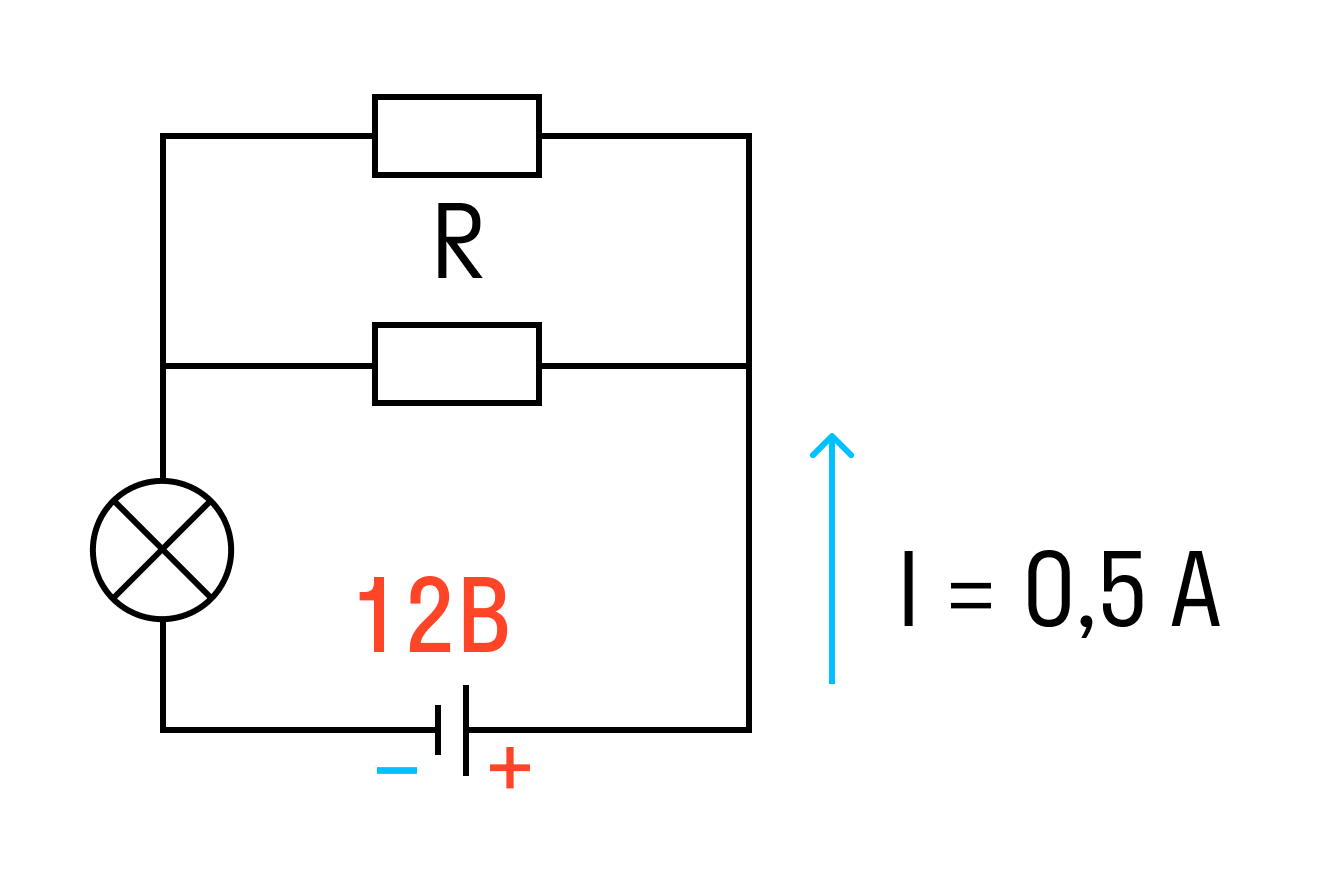
Наконец-то, последняя и самая сложная задача! В ней собрали все самое серьезное из этой статьи 💪.

Задачка четыре со звездочкой

К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.

Решение:

Найдем сначала сопротивление лампы.

Rлампы = R/2 = 10/2 = 5 Ом

Теперь найдем общее сопротивление двух параллельно соединенных резисторов.

Rрезисторов = (R * R)/R + R = R^2)/2R = R/2 = 10/2 = 5 Ом

И общее сопротивление цепи равно:

R = Rлампы + Rрезисторов = 5 + 5 = 10 Ом

Выразим внутреннее сопротивление источника из закона Ома для полной цепи.

r = 12/0,5 — 10 = 14 Ом

Ответ: внутреннее сопротивление источника равно 14 Ом.

Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!

Источник

Что такое электрическое сопротивление

Электрическое сопротивление – величина электротехническая, характеризующая степень препятствования свободному протеканию электронов по проводнику. Некоторые материалы могут иметь нулевое сопротивление, а некоторые наоборот, имеют высокое, такие материалы называются диэлектриками. Есть другая противоположность – сверхпроводники.

Измеряется сопротивление в Омах, в честь своего первооткрывателя. Есть производные единицы – килоОмы, мегаОмы и даже гигаОмы. Проводимость – величина обратная сопротивлению. В данной статье рассказано все о таком физическом явлении, как сопротивление, как его измерять и рассчитать. В качестве дополнения, материал содержит два ролика и один скачиваемый файл.

Электрическое сопротивление проводников

Любое тело, по которому протекает электрический ток, оказывает ему определенное сопротивление. Электронная теория так объясняет сущность электрического сопротивления металлических проводников.

Свободные электроны при движении по проводнику бесчисленное количество раз встречают на своем пути атомы и другие электроны и, взаимодействуя с ними, неизбежно теряют часть своей энергии. Электроны испытывают как бы сопротивление своему движению. Различные металлические проводники, имеющие различное атомное строение, оказывают различное сопротивление электрическому току.

Свойство материала проводника препятствовать прохождению через него электрического тока называется электрическим сопротивлением.

Точно тем же объясняется сопротивление жидких проводников и газов прохождению электрического тока. Однако не следует забывать, что в этих веществах не электроны, а заряженные частицы молекул встречают сопротивление при своем движении. Сопротивление обозначается латинскими буквами R или r. За единицу электрического сопротивления принят ом.

Ом есть сопротивление столба ртути высотой 106,3 см с поперечным сечением 1 мм2 при температуре 0° С. Если, например, электрическое сопротивление проводника составляет 4 ом, то записывается это так: R = 4 ом или r = 4ом. Для измерения сопротивлений большой величины принята единица, называемая мегомом. Один мегом равен одному миллиону ом.

Чем больше сопротивление проводника, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем легче электрическому току пройти через этот проводник. Следовательно, для характеристики проводника (с точки зрения прохождения через него электрического тока) можно рассматривать не только его сопротивление, но и величину, обратную сопротивлению и называемую, проводимостью.

Физический принцип сопротивления

Проще всего объяснить это по аналогии с водопроводной трубой. Представьте себе, что вода — некое подобие электрического тока, образуемого направленным движением электронов в проводнике, а напряжение — аналог давления (напора) воды. Сопротивление — это та сила противодействия среды их движению, которую электронам или воде приходится преодолевать, в результате чего производится работа и выделяется теплота. Именно такая модель представлялась в 1820-е годы Георгу Ому, когда он занялся исследованием природы происходящего в электрических цепях.

В водопроводной трубе всё обстоит так, что чем выше давление воды, тем относительно большая доля энергии расходуется на преодоление сопротивления в трубах, поскольку в них усиливается турбулентность потока. Из этого исходил Ом, приступая к опытам по измерению зависимости силы тока от напряжения. И очень скоро выяснилось, что ничего подобного в электрических проводниках не происходит: сопротивление вещества электрическому току вовсе не зависит от приложенного напряжения. В этом, по сути, и заключается закон Ома, который (для отдельного участка цепи) записывается очень просто:

где V — напряжение, приложенное к участку цепи, I — сила тока, а R — электрическое сопротивление участка цепи.

Сегодня мы понимаем, что электрическая проводимость обусловлена движением свободных электронов, а сопротивление — столкновением этих электронов с атомами кристаллической решетки. При каждом таком столкновении часть энергии свободного электрона передается атому, который, в результате, начинает колебаться более интенсивно, и в результате мы наблюдаем нагревание проводника под действием электрического тока. Повышение напряжения в цепи никак не сказывается на доле тепловых потерь такого рода, и соотношение напряжения и электрического тока остается постоянным.

Однако, когда Георг Ом экспериментально открыл свой закон, атомная теория строения вещества находилась в зачаточном состоянии, а до открытия электрона оставалось несколько десятилетий. Таким образом, для него формула V = IR была чисто экспериментальным результатом. Сегодня мы имеем достаточно стройную и, одновременно, сложную теорию электропроводности и понимаем, что закон Ома в его первозданном виде — всего лишь грубое приближение.

Роль проводника тока

Если к веществу или материалу обладающему проводящей способностью, подключить источник ЭДС, то по нему начинает протекать электрический ток. Свободные электроны вещества при этом начинают направленное движение от отрицательного полюса к положительному, т.к они являются носителями отрицательного заряда.

Во время направленного движения электроны ударяются об атомы материала и передают им некоторую часть своей энергии, из-за этого происходит нагрев проводника по которому проходит ток. А электроны после столкновения замедляют свое движение. Но электрическое поле их опять ускоряет, поэтому они продолжают свое направленное движение к плюсу.

Этот процесс может идти практически бесконечно, пока вокруг проводника имеется электрическое поле созданное источником электродвижущей силы. Получается, что чем больше препятствий попадется на пути следования электронов, тем выше значение сопротивления.

В различных веществах имеется разное количество свободных электронов, а атомы, между которыми свободные носители заряда перемещаются, обладают различным местом расположения. Поэтому сопр. проводников току зависит, в первую очередь от материала, из которого они сделаны, от площади и длины поперечного сечения.

Если сравнить два проводника сделанные из одинакового материала, то более длинный имеет большее R при равных площадях поперечных сечений, а с большим поперечным сечением имеет более низкое сопр. при равных длинах. Рассмотрим практический пример: Подключим лампочку накаливания на 60Вт в розетку с сетевым напряжением. Спираль лампочки начинает создавать потоку электронов с потенциалом в 220В некоторое препятствие.

Если эта преграда на пути электронов окажется слишком маленькой лампочка перегорит. Если слишком большое – накальная нить будет гореть очень слабо. А вот если оно будет “оптимальное, тогда лампочка будет гореть нормально, выделяя при этом и тепло. Вырабатываемое тепло называют “потерянной” энергией, так как часть энергию затрагивается на никому ненужный нагрев.

Что такое электрическое удельное сопротивление? Из формулы закона Ома можно записать, что электрическое сопротивление является физической величиной, которую можно вычислить как отношение напряжения в проводнике к силе протекающего в нем тока.

Итак, исходя из опыта с лампочкой чуть выше можно сделать вывод, что электрическое сопротивление проводника является физической величиной, которая указывает на свойство вещества преобразовывать электрическую энергию в тепловую. (R= ρ × l)/S ρ — удельное сопротивление материала проводника, Ом·м, l — длина, м, и S — площадь сечения, м2. Удельное электрическое сопротивление является также физической величиной, которая равна сопротивлению метрового проводника с площадью сечения в один метр квадратный. На практике, сечение измеряют в квадратных миллиметрах.

Поэтому и удельное электрическое сопротивление проще считать в Ом × мм2 / м, а площадь подставлять в мм2. Формула выше говорит о том, что удельное сопр. прямо пропорционально удельному сопр. материала, из которого он сделан, а также его длине и обратно пропорционально площади поперечного сечения проводника.

Сопр. проводников зависит также от температуры. Так у элементов из металла с повышением температуры R увеличивается. Зависимость эта сложная, но в относительно узких пределах температурного изменения (примерно до 200° Цельсия) можно условно считать, что для каждого металла существует определенный, так называемый температурный, коэффициент сопротивления (альфа), который выражает определенный прирост сопротивления дельта r при изменении температуры на один градус цельсия, отнесенный к 1 ом начального значения сопротивления. Таким образом, температурный коэффициент удельного сопротивления будет равен α = r2-r1/r1(T2-T1) и прирост сопр. будет равен Δr=r2-r1=αr2(T2-T1)

Во-первых, от материала проводника. Чем больше значение ρ, тем хуже будет пропускная токовая способность. Во-вторых, от длины провода – с увеличением длины сопротивление увеличивается. В-третьих, от толщины. У более толстого проводника, более низкое сопротивление. И в-четвертых, от температуры проводника.

Если он из металла, то их удельное сопротивление возрастает с ростом температуры. В исключение можно поместить специальные сплавы – их электрическое удельное сопр. практически не изменяется при нагревании. Например: никелин, константан и манганин. А вот у жидкостей с нагревом, удельное сопротивление уменьшается.

Связь с удельной проводимостью в изотропных материалах, выражется формулой: ρ = 1 / σ Где σ – удельная проводимость. Явление сверхпроводимости Предположим температуру материала будем уменьшать, то удельное сопротивление при этом будет также снижаться. Есть предел, до которого можно снизить температуру – абсолютный нуль.

В численном выражении равен —273°С. Ниже этого значения температур просто не существует. При этом значении удельное сопротивление любого проводника будет равно нулю. так как при абсолютном нуле атомы кристаллической решетки полностью перестают колебаться. В результате электронное облако проходит между узлами решетки, не соударяясь с ними. Удельное сопр. материала становится равным нулю, что открывает возможности для получения бесконечно огромных токовых уровней в проводниках малого сечения. Явление сверхпроводимости открывает фантастические перспективы для развития электротехники и электронной техники. Но пока еще имеются некоторые сложности, связанные с получением в быту сверхмалых температурных значений, требуемых для создания нужного эффекта. Когда эти проблемы смогут преодалеть, электротехника шагнет на принципиально новый уровень развития.

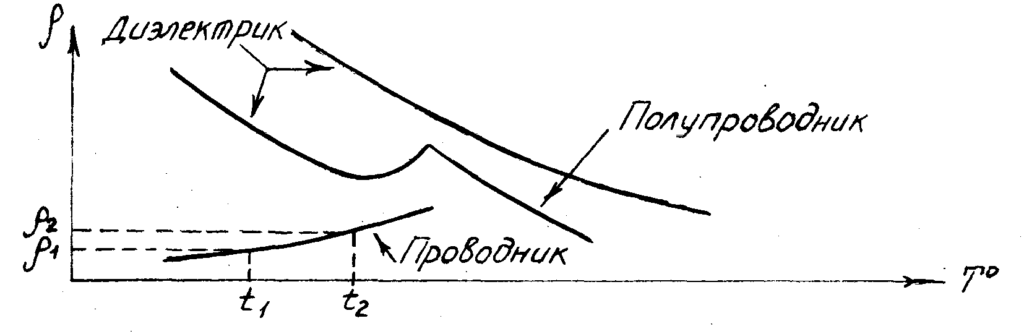
Зависимость сопротивления от температуры

Электропроводность всех материалов зависит от их температуры. В металлических проводниках при нагревании размах и скорость колебаний атомов в кристаллической решетке металла увеличиваются, вследствие чего возрастает и сопротивление, которое они оказывают потоку электро­нов. При охлаждении происходит обратное явление: беспорядоч­ное колебательное движение атомов в узлах кристаллической решетки уменьшается, сопротивление их потоку электронов пони­жается и электропроводность проводника возрастает.

В природе, однако, имеются некоторые сплавы: фехраль, константан, манганин и др., у которых в определенном интервале температур электрическое сопротивление меняется сравнительно мало. Подобные сплавы применяют в технике для изготовления различных резисторов, используемых в электроизмерительных при­борах и некоторых аппаратах для компенсации влияния темпера­туры на их работу.

О степени изменения сопротивления проводников при измене­нии температуры судят по так называемому температурному ко­эффициенту сопротивления а. Этот коэффициент представляет собой относительное приращение сопротивления проводника при увеличении его температуры на 1 °С. В табл. 1 приведены значения температурного коэффициента сопротивления для наиболее приме­няемых проводниковых материалов.

Сопротивление металлического проводника R_t при любой тем­пературе t

где R — сопротивление проводника при некоторой начальной температуре t (обычно при + 20 °С), которое может быть подсчитано по формуле (5);

t— t — изменение температуры.

Свойство металлических проводников увеличивать свое сопро­тивление при нагревании часто используют в современной технике для измерения температуры. Например, при испытаниях тяговых двигателей после ремонта температуру нагрева их обмоток определяют измерением их сопротивления в холодном состоянии и после работы под нагрузкой в течение установленного периода (обычно в течение 1 ч).

Исследуя свойства металлов при глубоком (очень сильном) охлаждении, ученые обнаружили замечательное явление: вблизи абсолютного нуля (— 273,16 °С) некоторые металлы почти пол­ностью утрачивают электрическое сопротивление. Они становятся идеальными проводниками, способными длительное время пропус­кать ток по замкнутой цепи без всякого воздействия источника электрической энергии.

Это явление названо сверхпроводимостью. В настоящее время созданы опытные образцы линий электропере­дачи и электрических машин, в которых используется явление сверхпроводимости. Такие машины имеют значительно меньшие мас­су и габаритные размеры по сравнению с машинами общего назна­чения и работают с очень высоким коэффициентом полезного дей­ствия.

Источник