Что такое объем понятия в математике

Лекция 6. Объем и содержание понятия. Отношения между понятиями.

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Лекция 4. Объем и содержание понятия. Отношения между понятиями.

Всякий математический объект обладает определенными свойствами. Например, квадрат имеет четыре стороны, четыре прямых угла и др. Различают свойства существенные и несущественные.

Для квадрата: АВСД существенные свойства: АВ = ВС = СД =ДА,

Если квадрат повернуть, сохранятся только существенные свойства, именно они и составляют понятие об объекте.

Рассмотрим пример для дошкольников, используя наглядный материал

— Маленький черный треугольник.

— Большой белый треугольник.

— Чем фигуры отличаются?

— Что есть у треугольника?

Совокупность всех существеннных свойств объекта называют содержанием понятия.

Совокупность всех объектов, обозначаемая одним термином, составляет объем понятия.

Итак, любое понятие характеризуется:

— объемом (совокупность всех объектов, называемых этим термином);

— содержанием (совокупность всех существенных свойств объектов, входящих в объем понятия).

Между объемом понятия и его содержанием существует связь: чем «больше» объем понятия, тем «меньше» его содержание, и наоборот. Объем понятия «треугольник» «больше», чем объем понятия «прямоугольный треугольник», так как все объекты второго понятия являются и объектами первого понятия. Содержание понятия «треугольник» «меньше», чем содержание понятия «прямоугольный треугольник», так как прямоугольный треугольник обладает всеми свойствами любого треугольника и еще другими свойствами, присущими только ему.

Для распознавания объекта необязательно проверять у него все существенные свойства, достаточно лишь некоторых. Этим пользуются, когда понятию дают определение.

Определение понятия – это логическая операция, которая раскрывает содержание понятия либо устанавливает значение термина. Определение понятия позволяет отличать определяемые объекты от других объектов. Так, например, определение понятия «прямоугольный треугольник» позволяет отличить его от других треугольников.

Различают явные и неявные определения. Явные определения имеют форму равенства двух понятий. Одно из них называют определяемым другое определяющим.

Следует иметь в виду, что понятия рода и вида относительны. Так, «прямоугольник» – это родовое к понятию «квадрат», но видовое по отношению к понятию «четырехугольник».

Кроме того, для одного понятия могут существовать несколько родовых. Например, для квадрата родовыми являются ромб, четырехугольник, многоугольник, геометрическая фигура. В определении через род и видовое отличие для определяемого понятия принято называть ближайшее родовое понятие.

Таким образом, определение через род и видовое отличие имеет следующую структуру:

Определяемое = Род + Видовое

Задания для самостоятельной работы по теме:

1. Каков объем понятий: «цифра», «автомобиль», «снегурочка», «волк», «столица России», «двузначное число».

2. Решите анаграммы. Исключите лишнее слово. Ответ обоснуйте:

Источник

Глава III. Содержание и объём понятий

Признаки понятий. Понятия в психологии получаются из сравнений сходных представлений. Представления в свою очередь складываются из отдельных элементов. Составные элементы представления или понятия принято называть признаками. Признаки есть то, чем одно представление или понятие отличается от другого. Например, признаками золота мы считаем «металл», «драгоценный», «имеющий определённый удельный вес» и т.п. Это всё то, чем золото отличается от других вещей, от не-металлов, от недрагоценных металлов и т.п.

Не все признаки нужно считать равноценными. Каждое понятие имеет множество различных признаков, но при мышлении о нём мы прежде всего по преимуществу мыслим только известные признаки. Эти признаки являются как бы основными, около которых группируются другие признаки. Первые признаки называются существенными, или основными, а остальные – второстепенными. Основные признаки – это такие признаки, без которых мы не можем мыслить известного понятия и которые излагают природу предмета. Например, для ромба существенным является тот признак, что он есть четырёхугольник с параллельными и равными сторонами и т.п.; несущественным для понятия ромба является тот признак, что он имеет ту или другую величину сторон, ту или другую величину углов.

Признаки понятий со времени Аристотеля принято делить на следующие 5 классов:

1. Родовой признак. Если мы скажем, что химия есть наука, то наука будет родовым признаком для понятия «химия»; в числе других признаков, присущих понятию «химия», есть и признак «наука»; этот признак отличает химию от всего, что не есть наука. Род (genus) или родовой признак есть понятие класса, в который мы вводим другое рассматриваемое нами понятие.

2. Видовое различие. Если мы скажем, что химия есть наука, занимающаяся изучением строения вещества, то прибавление признака – «занимающаяся изучением строения вещества» будет служить для обозначения того, чем эта наука отличается от других наук. Такой признак, который служит для того, чтобы выделять понятие из ряда ему подобных понятий, называется видовым различием (differentia specifica). Возьмём понятия «моряк русский», «моряк французский», «моряк английский». В этом случае «русский», «французский», «английский» есть видовое различие; оно служит для того, чтобы выделить моряка одной нации от моряков всех прочих наций.

3. Вид (species). Если к родовому признаку присоединить видовое различие, то получится вид. Например, «здание для склада оружия» – арсенал; «здание для склада хлеба» – амбар. В этом случае «здание» есть род, «для хранения оружия» есть видовое различие; присоединение к роду видового различия даёт вид «арсенал». Присоединение к понятию «здание» видового признака «служащее для хранения хлеба» даёт вид «амбар». Вид может быть признаком, потому что его можно приписать понятию. Например, «эта наука есть химия».

4. Собственный признак (proprium). Собственный признак – это такой признак, который присущ всем вещам данного класса, который не содержится в числе существенных признаков, но который может быть выведен из них. Например, существенным признаком человека является его «разумность». Из этого свойства вытекает его способность владеть речью. Этот последний признак есть собственный признак. Основной признак треугольника – это прямолинейная плоская фигура с тремя сторонами. Что же касается того признака треугольника, что сумма углов его равняется двум прямым, то это есть его собственный признак, потому что вытекает или выводится из основных признаков. Мы этого признака не мыслим, когда думаем о треугольнике, поэтому он является выводным.

5. Несобственный признак (accidens). Несобственный признак – это такой признак, который не может быть выведен из существенного признака, хотя и может быть присущ всем вещам данного класса. Например, чёрный цвет ворона есть accidens. Если бы чёрный цвет ворона был выводим из основных свойств его, то он мог бы быть назван proprium, но он не выводим, так как мы не знаем, по какой причине вороны имеют чёрный цвет перьев. Он есть, следовательно, accidens.

Несобственные признаки делятся на две группы: на неотделимые несобственные признаки (accidens inseparabile) и отделимые несобственные признаки (accidens separabile). Последние суть те признаки, которые присущи только некоторым вещам того или другого класса, но не всем, а первые присущи всем вещам данного класса. Например, чёрный цвет ворона есть accidens inseparabile. Чёрный цвет волос для человека есть accidens separabile, потому что есть люди, которые не имеют чёрного цвета волос. По отношению к отдельным индивидуумам несобственный признак также может быть отделимым и неотделимым. Отделимые – это такие признаки, которые одно время имеются налицо, а в другое время не имеются. Например, Бальфур – первый министр Англии. Через некоторое время он может не быть первым министром. Это есть признак отделимый. «Лев Толстой родился в Ясной Поляне». В этом предложении признак «родился в Ясной Поляне» есть неотделимый признак.

Содержание и объём понятий. Понятия могут быть рассматриваемы с точки зрения содержания и объёма.

Содержание понятия – это то, что мыслится в понятии. Например, в понятии «сахар» мыслятся признаки: сладкий, белый, шероховатый, имеющий тяжесть и т.д.; эти признаки в совокупности и составляют содержание понятия «сахар». Содержание понятия, другими словами, есть сумма признаков его; поэтому каждое понятие можно разложить на ряд присущих ему признаков. Содержание понятия может быть весьма изменчивым в зависимости от принятой точки зрения, от размера знания и т.п. Например, в понятии «сахар» химик мыслит одно содержание, а нехимик – другое.

Объём понятия есть то, что мыслится посредством понятия, т.е. объём понятия есть сумма тех классов, групп, родов, видов и т.п., к которым данное понятие может быть приложено. Например, объём понятия «животное»: птица, рыба, насекомое, человек и т.д.; объём понятия «элемент»: кислород, водород, углерод, азот и т.д.; объём понятия «четырёхугольник»: квадрат, прямоугольник, ромб, трапеция.

Таким образом, различие между объёмом понятия и содержанием понятия сводится к следующему: объём понятия означает ту совокупность предметов, к которым должно прилагаться данное понятие, а содержание обозначает те признаки, которые приписываются тому или другому понятию.

Для более ясного представления объёма понятий и отношения объёмов существует особый приём, называемый «логической символикой».

На рис. 1 большой круг символизирует собой понятие «элемент», а меньшие круги, в нём находящиеся, символизируют понятия, входящие в его объём. Если мы изображаем какой-нибудь круг внутри другого круга, то мы этим символизируем, что объём одного понятия входит в объём другого.

Из рис. 2 видно, что понятие «дерево» содержит в своём объёме понятия «дуб», «ель» и т.п. Отдельные точки в круге «ель» символизируют индивидуальные, или единичные, ели.

Понятие с большим объёмом называется родом по отношению к тому понятию с меньшим объёмом, которое входит в его объём. Понятие с меньшим объёмом в этом случае называется видом. Понятия с большим объёмом можно назвать также понятиями более широкими или более общими.

Любой вид может сделаться родом. Например, понятие «пальма» относится к понятию «дерево», как вид к роду, но в свою очередь оно относится уже как род к своим видам – «пальма кокосовая», «пальма фиговая» и т.д. Вообще более общее понятие есть род для менее общего понятия; более общее понятие представляет собой родовое понятие для менее общего, менее общее само становится родом для ещё менее общего и т.д., пока мы не придём к такому понятию, которое уже не может в своём объёме содержать какие-либо другие виды, а может подразделяться только на отдельные индивидуумы.

Следует упомянуть о попытке греческого философа Порфирия (233–304) при помощи схемы облегчить понимание отношения между охватывающими друг друга понятиями, т.е. понятиями, из которых одно входит в объём другого. Эта схема называется «деревом Порфирия». В понятие «бытия» (т.е. того, что вообще существует) входит понятие «телесного бытия» и «бестелесного бытия». Тело содержит в своём объёме одушевлённое тело, или организм, и неодушевлённое тело. Понятие «организм» содержит в своём объёме чувствующие и нечувствующие организмы (растения). Чувствующие организмы содержат в своём объёме разумные и неразумные существа и т.д. (рис. 3).

Бытие есть высший род, который уже не может быть видом для другого рода. Такой род называется summum genus; человек – это низший вид. В его объём уже не входят понятия с меньшим объёмом, а входят только отдельные индивидуумы. Такое понятие называется infima species (самый низший вид). Ближайший высший класс (или род) того или другого вида называется proximum genus (ближайший род). Отношение между более широкими и узкими понятиями можно изобразить и иначе, именно, поместив круги, служащие для обозначения понятий с меньшим объёмом, внутри кругов, служащих для обозначения понятий с большим объёмом (рис. 3а).

Ограничение и обобщение. Процесс образования менее общих понятий из более общих называется ограничением (determinatio). Для образования менее общего понятия мы должны к более общему прибавить несколько признаков, благодаря чему понятие уясняется (determinatur). Например, чтобы из понятия «дерево» получить менее общее понятие «пальма», надо к признакам дерева прибавить специальные признаки пальмы: вид её листьев, прямизну ствола и т.д. Обратный процесс образования более общего понятия из менее общего, при котором, наоборот, некоторое количество признаков от данного понятия отнимается, называется обобщением (generalisatio).

Род образуется из видов при помощи процесса обобщения, и, наоборот, виды образуются из родов при помощи процесса ограничения. Эти процессы мы можем изобразить при помощи следующей схемы:

Предположим, что у нас есть понятие A (наука). Из него при помощи видового различия a мы можем образовать вид Aa (математика); прибавив к понятию Aa видовое различие b (определение пространственных отношений), получим геометрию Aab. Прибавив к этому виду признак c (определение пространственных отношений на плоскости), получим планиметрию Aabc.

Обратный процесс – получение более общих понятий путём отбрасывания отдельных признаков – будет называться обобщением. И тот и другой процесс можно изобразить при помощи следующей схемы, в которой стрелки показывают или нисхождение от более общих понятий к менее общим или, наоборот, восхождение от менее общих к более общим понятиям.

Отношение между объёмом и содержанием понятия. Для того чтобы ответить на вопрос, какое существует отношение между объёмом и содержанием понятия, возьмём какой-нибудь пример. Объём понятия «человек» обширнее, чем, например, объём понятия «негр». Употребляя понятие «человек», мы думаем обо всех людях, мы думаем о людях, живущих во всех пяти частях света, между прочим и в Африке. Употребляя понятие «негр», мы думаем только о тех людях, которые живут в Африке. Но о содержании этих двух понятий следует сказать как раз наоборот: содержание понятия «негр» будет обширнее содержания понятия «человек». Когда мы говорим о негре, то мы можем найти в нём все признаки понятия «человек» плюс ещё некоторые особенные признаки, как-то: чёрный цвет кожи, курчавые волосы, приплюснутый нос, толстые губы и т.п.

Итак, по мере увеличения содержания понятия уменьшается его объём, и наоборот.

Вопросы для повторения

Что такое признаки понятий? Какие признаки понятий мы отличаем? Что такое родовой признак? Что такое видовое различие? Что такое вид? Что такое собственный признак? Что такое несобственный признак? Что такое содержание понятия? Что такое объём понятия? Что такое summum genus? Что такое infima species? Что такое обобщение? Что такое ограничение? Какое существует отношение между объёмом и содержанием понятия?

Источник

С точки зрения языка вербальные определения являются пове­ствовательными предложениями, но не являются высказываниями в смысле математической логики. Относительно этих предложений не имеет смысла говорить истинны они или ложны. С логической точки зрения вербальные определения ближе к повелительным, чем повествовательным предложениям.

Рассмотрим некоторые способы вербальных определений.

1. Определение понятий через род и видовое отличие. Этот способ определения является наиболее распространенным, ему принадлежит ведущая роль в классической логике Аристотеля, поэтому его часто называют классическими. Логическая структура определений через род и видовое отличие проста, четко выражена и поэтому впол­не доступна учащимся уже в начальных классах школы.

Уже из приведенных примеров видна их общая структура. В опре­делении указываются: некоторое множество (род), которому принадлежит определяемое понятие; свойство, которое выделяет определяемый объект из объектов этого же рода (видовое отличие).

2. Генетическое определение понятий.

Генетические или конструктивные определения являются част­ным случаем определений через род и видовое отличие. В таких определениях видовое отличие указывает на происхождение опреде­ляемого объекта (отношения) или на способ его образования.

Рассмотрим следующее определение: «Циклоидой называется кривая линия, которую описывает любая точка окружности, катящейся по прямой без скольжения». Родовым здесь является понятие «кривая линия», а видовое от­личие указывает на способ образования определяемой кривой.

3. Рекурсивные определения.

В последнее время в математике, ее приложениях, а также в других науках все чаще встречаются, так называемые, рекурсивные определения. В таких определениях указываются некоторые основ­ные элементы из объема понятия и даются правила, позволяющие по­лучать новые элементы из уже имеющихся. Примером рекурсивного определения является определение 2.6 логической формулы. Рекур­сивные определения находят особенно широкое применение в языках программирования на ЭВМ.

Определения объектов и отношений путем указания их свойств называются дискрипциями. Примером дискрипции является опреде­ление 3.28 из §10. «Бинарное отношение р на множестве Xназывается отношением эквивалентности, если оно обладает свойствами: рефлексивности («хÎХ)(хрх); симметричности («х, у Î Х)(хру Þ урх) ; транзитивности («x, у, z Î Х)(хру Ù ypz Þ xpz)«

Здесь родовым является понятие » бинарное отношение», а видо­вое отличие представлено перечислением свойств определяемого от­ношения.

5. Аксиоматические определения.

Если какое-то понятие вводится с помощью списка аксиом, опи­сывающих свойства этого понятия, то такое определение называется аксиоматическим. Примером аксиоматического определения являет­ся следующее: «Умножением натуральных чисел называется алгебраическая опе­рация, определенная на множестве N натуральных чисел и удовле­творяющая аксиомам: 1) («а Î N)( a * 1 = а) ; 2) («a, bÎN) (a*b’ = a*b+a)»

7.4. Корректные и некорректные определения.

Для того, чтобы определения могли служить построению какой-либо научной теории, они должны удовлетворять определенным требовани­ям. Одним из самых важных таких требований является требование соразмерности определения. Это означает, что объем определяемого понятия должен совпадать с объемом определяющего понятия. Боль­шинство ошибок в определениях приводит к нарушению соразмерно­сти его частей.

Таким образом, ни одно из приведенных предложений не явля­ется определением, так как в обоих случаях нарушено требование соразмерности.

Другим важным требованием, предъявляемым к определениям, является отсутствие порочного круга. Нарушение этого требования проявляется в том, что определяемое понятие содержится в опреде­ляющем или в цепочке последовательных определений используют­ся термины, ранее определенные через определяемое. Поэтому, если указанное требование не выполняется, то процедура определения по­нятий «зацикливается» и не сводится к исходным понятиям.

В качестве примеров рассмотрим предложения:

2) «Шаром называется часть пространства, ограниченная сферой», «Сферой называется граница шара».

Следующим требованием, выполнение которого необходимо для определений, является отсутствие омонимии. Каждый термин в качестве определяемого должен встречаться не более одного раза. При нарушении этого условия нарушается однозначность определения, один и тот же термин будет обозначать различные объекты или отно­шения. Нарушение этого требования особенно опасно в начале изуче­ния курса, так как создает неразбериху и вызывает дополнительные трудности при его усвоении.

В математической литературе до сих пор сохраняются некоторые омонимии. Например, слово «цифра» понимается как символ для записи числа и как соответствующее однозначное число.

При определении понятий желательно выполнение еще одного условия. Формулировка определения не должна содержать лишних свойств, которые можно вывести из других свойств, указанных в том же определении.

Рассмотрим в качестве примера определение: «Натуральное чи­сло называется простым, если оно имеет только два делителя и де­лится только на себя и единицу».

Совершенно очевидно, что условие «иметь только два делителя» вытекает из условия «делиться только на себя и на единицу», и на­оборот, а поэтому одно из этих условий является лишним.

Если определение удовлетворяет перечисленным выше условиям, то его называют корректным.

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Объем и содержание понятия. Отношения между понятиями

Всякий математический объект обладает определенными свойствами. Например, квадрат имеет четыре стороны, четыре прямых угла, равные диагонали. Можно указать и другие его свойства.

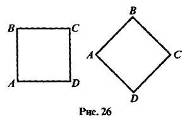
Среди свойств объекта различают существенные и несущественные. Свойство считают существенным для объекта, если оно присуще этому объекту и без него он не может существовать. Например, для квадрата существенными являются все свойства, названные выше. Несущественно для квадрата ABCD свойство «сторона AD горизонтальна». Если квадрат повернуть, то сторона AD окажется расположенной по-другому (рис. 26).

Поэтому, чтобы понимать, что представляет собой данный математический объект, надо знать его существенные свойства.

Когда говорят о математическом понятии, то обычно имеют в виду множество объектов, обозначаемых одним термином (словом или группой слов). Так, говоря о квадрате, имеют в виду все геометрические фигуры, являющиеся квадратами. Считают, что множество всех квадратов составляет объем понятия «квадрат».

Любое понятие имеет не только объем, но и содержание.

Содержание понятия- это множество всех существенных свойств объекта, отраженных в этом понятии.

Рассмотрим, например, понятие «прямоугольник».

Между объемом понятия и его содержанием существует взаимосвязь: если увеличивается объем понятия, то уменьшается его содержание, и наоборот. Так, например, объем понятия «квадрат» является частью объема понятия «прямоугольник», а в содержании понятия «квадрат» содержится больше свойств, чем в содержании понятия «прямоугольник» («все стороны равны», «диагонали взаимно перпендикулярны» и др.).

Любое понятие нельзя усвоить, не осознав его взаимосвязи с другими понятиями. Поэтому важно знать, в каких отношениях могут находиться понятия, и уметь устанавливать эти связи.

Отношения между понятиями тесно связаны с отношениями между их объемами, т.е. множествами.

Условимся понятия обозначать строчными буквами латинского алфавита: а, b, с. z.

Пусть заданы два понятия а и b. Объемы их обозначим соответственно А и В.

Если А = В, то говорят, что понятия а и b тождественны.

Например, тождественны понятия «равносторонний треугольник» и «равноугольный треугольник», так как их объемы совпадают.

Если множества А и В не связаны отношением включения, то говорят, что понятия а и b не находятся в отношении рода и вида и не тождественны. Например, не связаны такими отношениями понятия «треугольник» и «прямоугольник».

Во-вторых, для данного понятия часто можно указать несколько родовых понятий. Так, для понятия «прямоугольник» родовыми являются понятия «четырехугольник», «параллелограмм», «многоугольник». Среди них можно указать ближайшее. Для понятия «прямоугольник» ближайшим является понятие «параллелограмм».

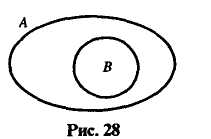
В-третьих, видовое понятие обладает всеми свойствами родового понятия. Например, квадрат, являясь видовым понятием по отношению к понятию «прямоугольник», обладает всеми свойствами, присущими прямоугольнику.

Установим, например, отношения между следующими парами понятий а и Ь, если:

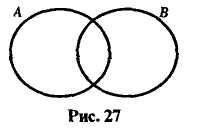
В случае 1) объемы понятий пересекаются, но не одно множество не является подмножеством другого (рис. 27).

Следовательно, можно утверждать, что данные понятия а и b не находятся в отношении рода и вида.

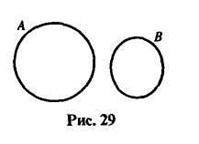
В случае 3) объемы понятий не пересекаются, так как ни про один отрезок нельзя сказать, что он является прямой, и ни одна прямая не может быть названа отрезком (рис. 29).

Следовательно, данные понятия не находятся в отношении рода и вида.

О понятиях «прямая» и «отрезок» можно сказать, что они находятся в отношении целого и части: отрезок- часть прямой, а не ее вид. И если видовое понятие обладает всеми свойствами родового понятия, то часть не обязательно обладает всеми свойствами целого. Например, отрезок не обладает таким свойством прямой, как ее бесконечность.

Источник