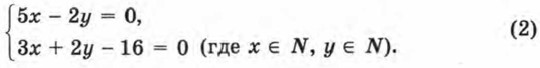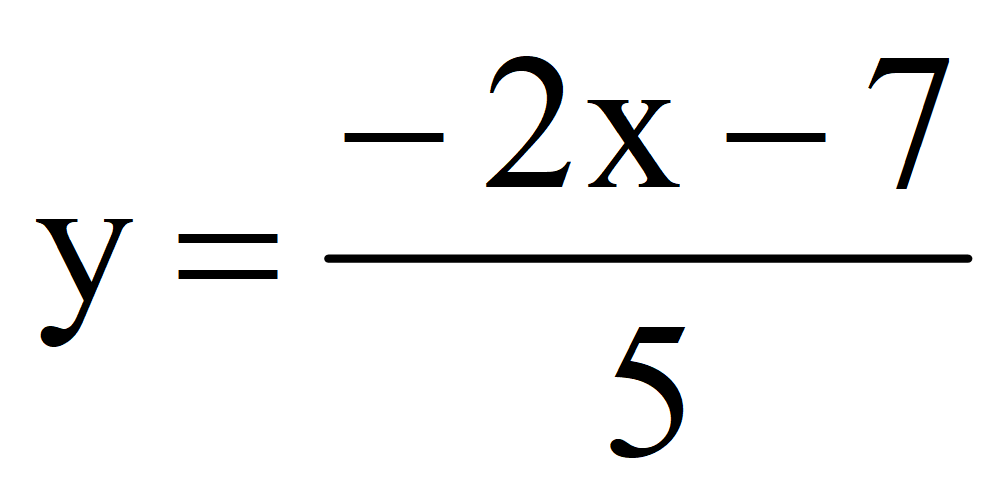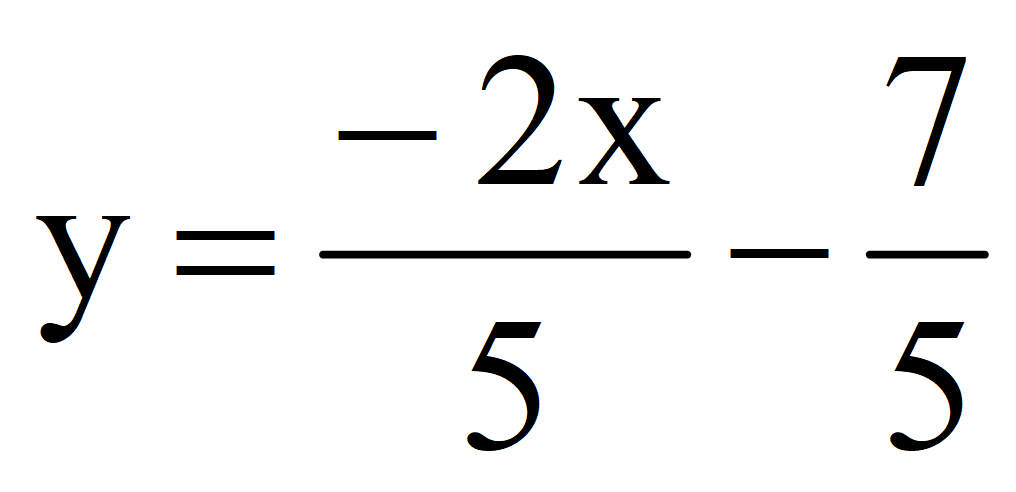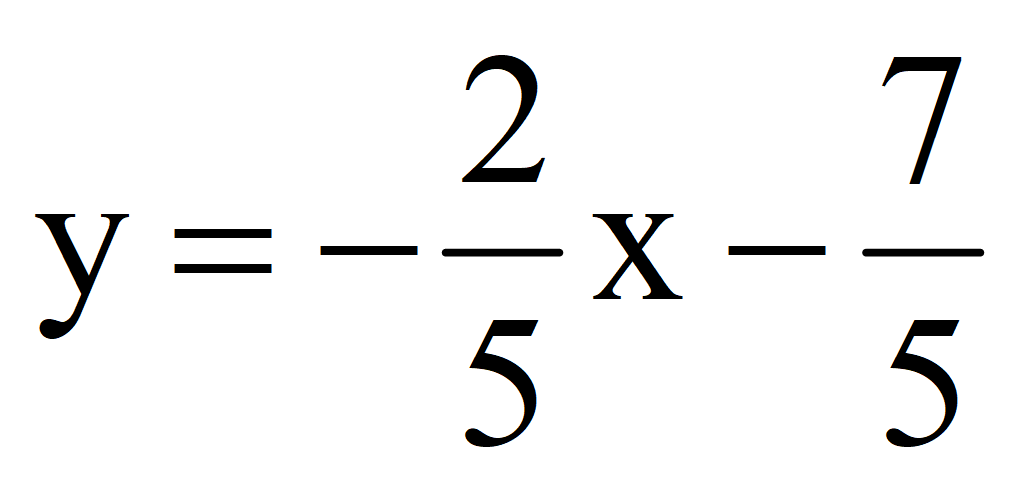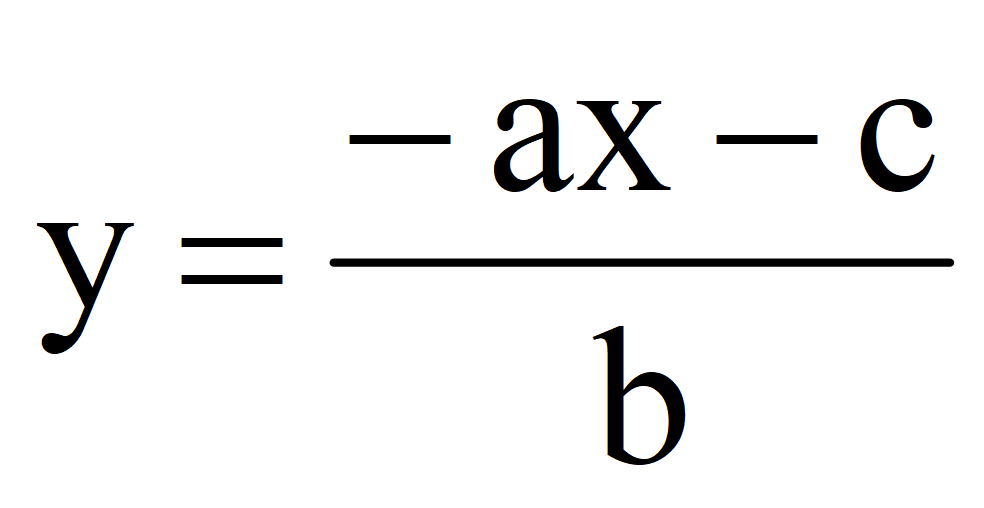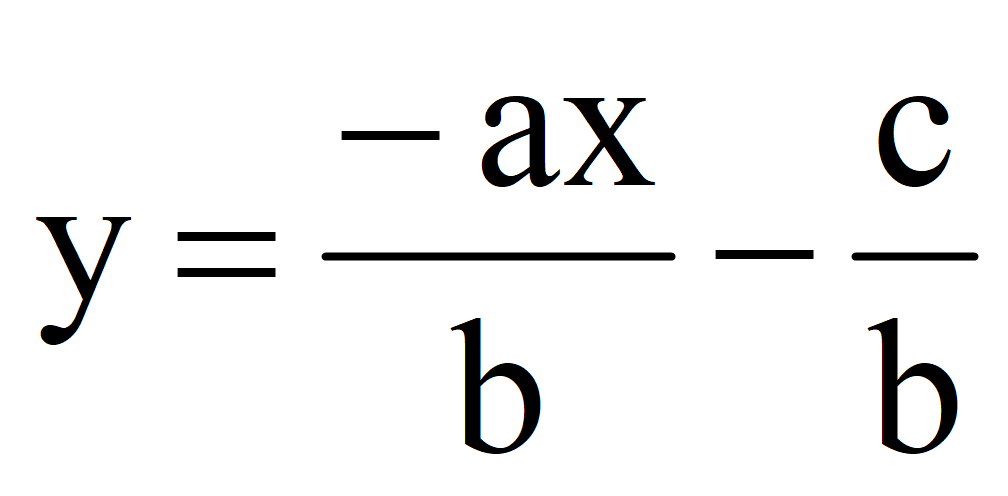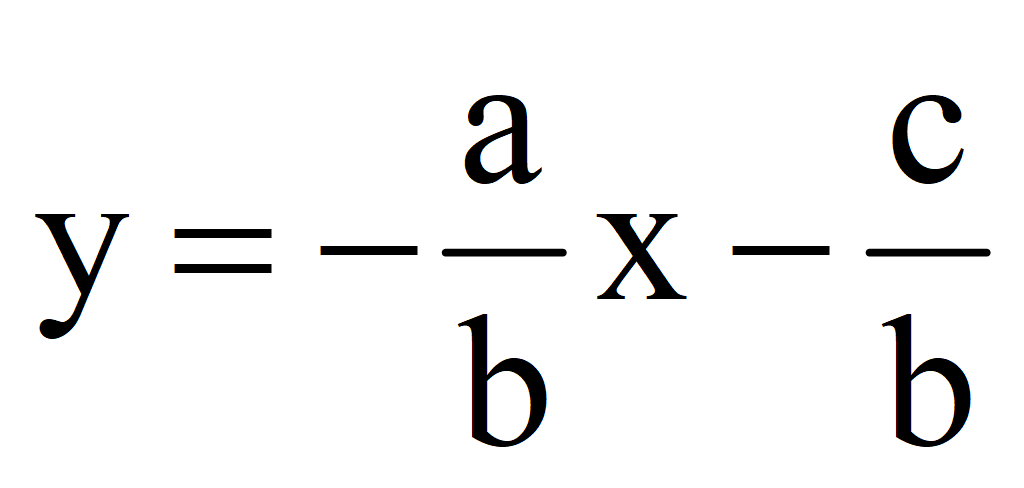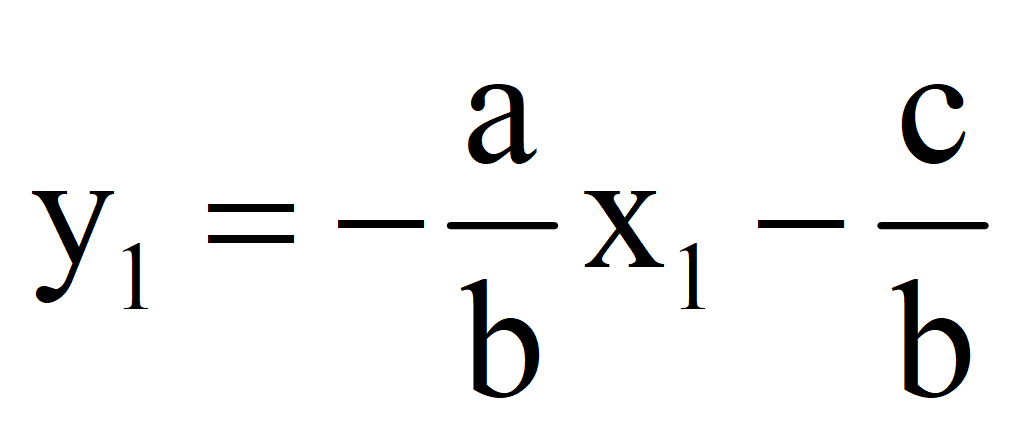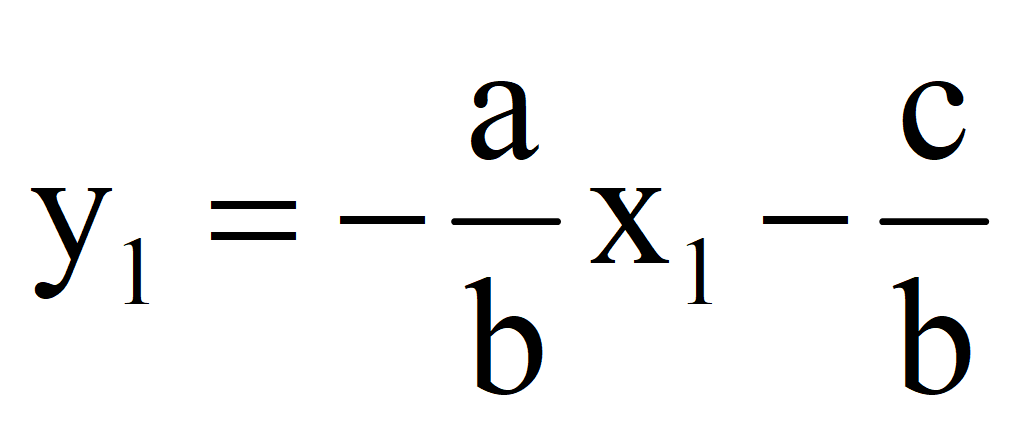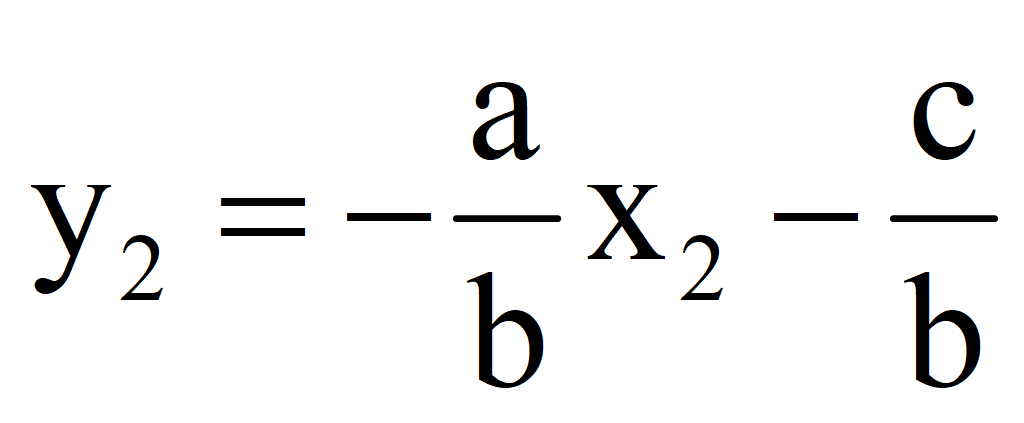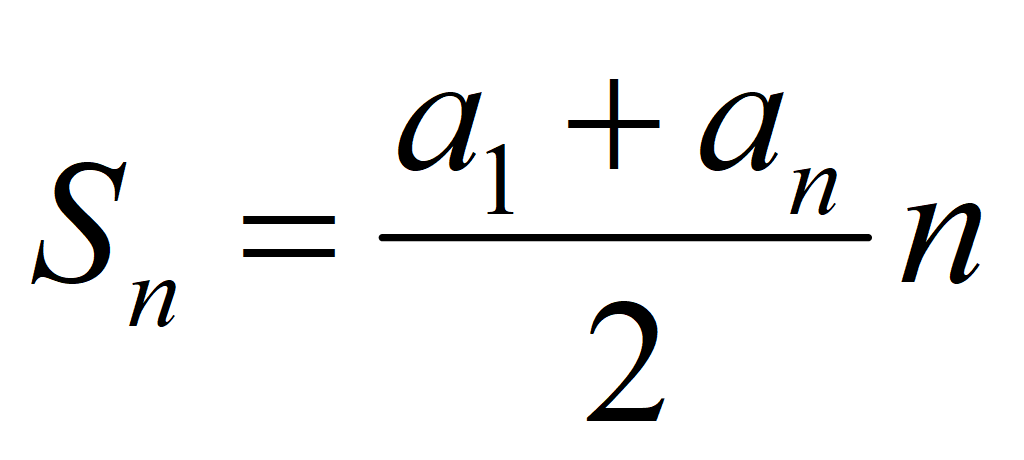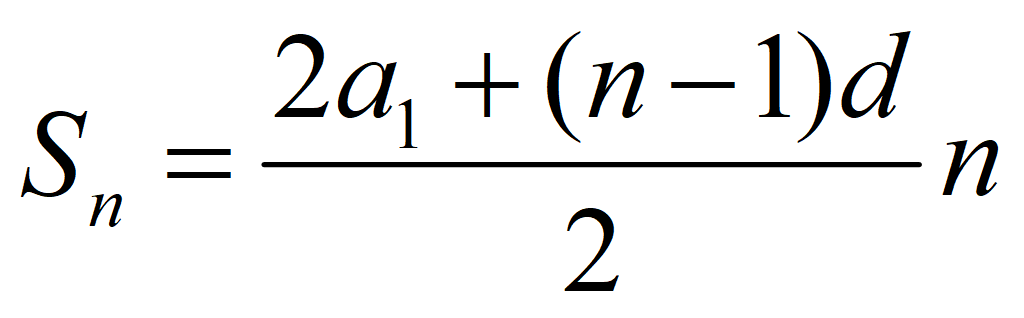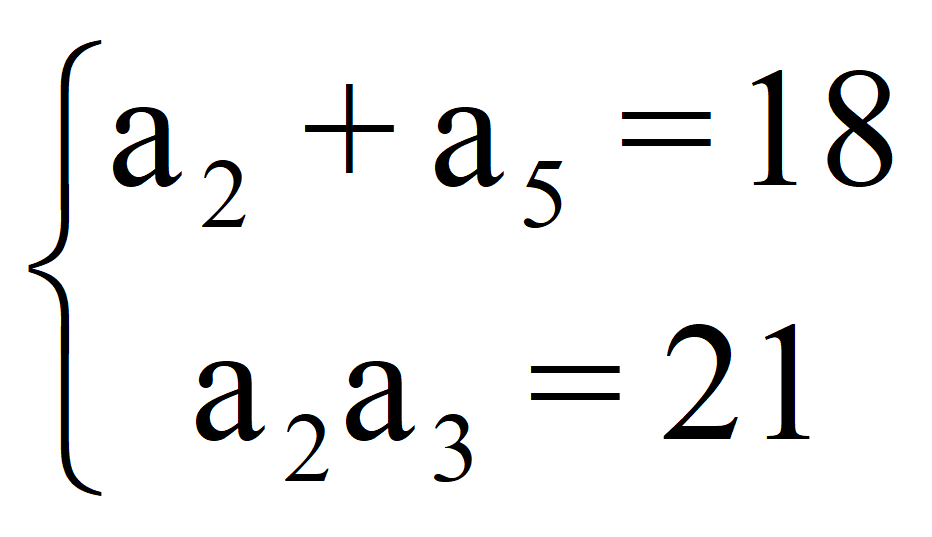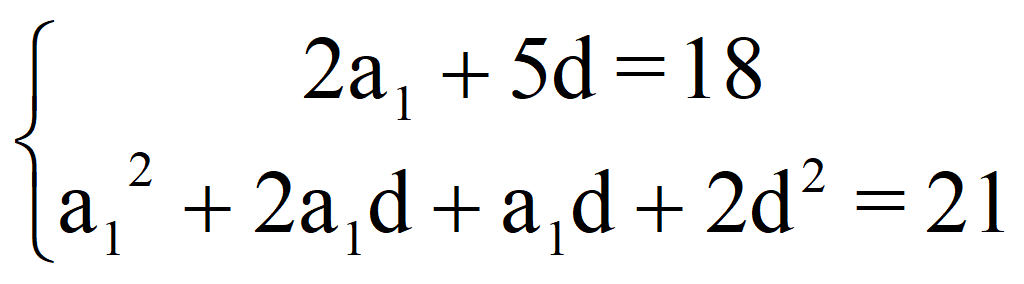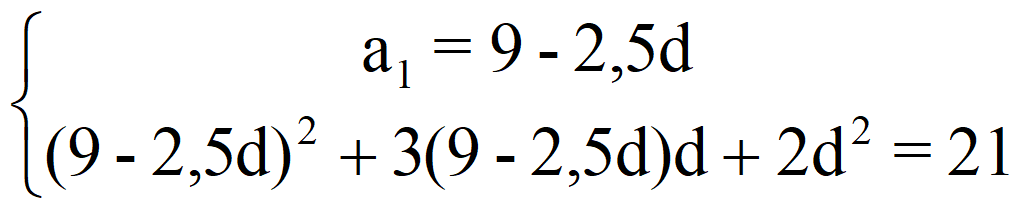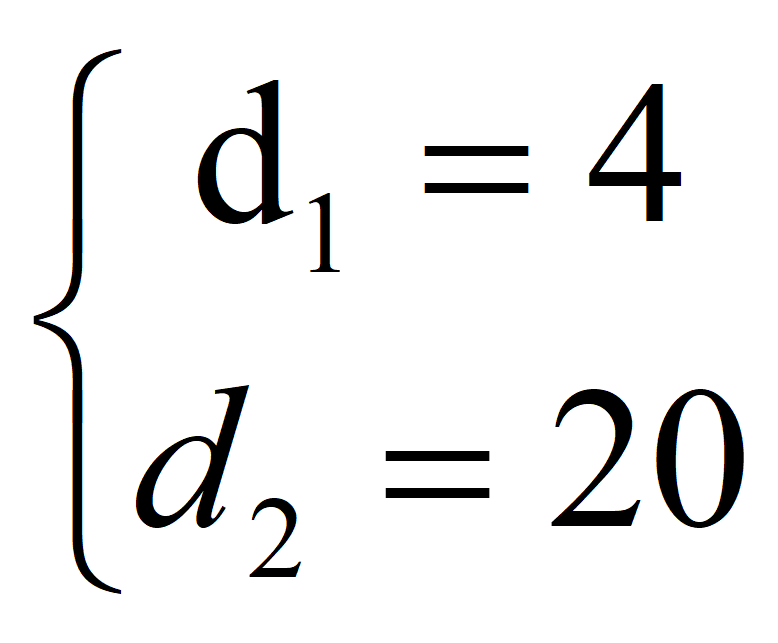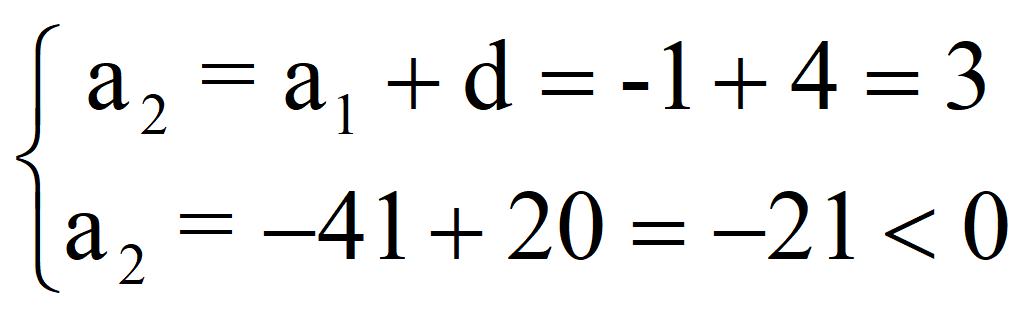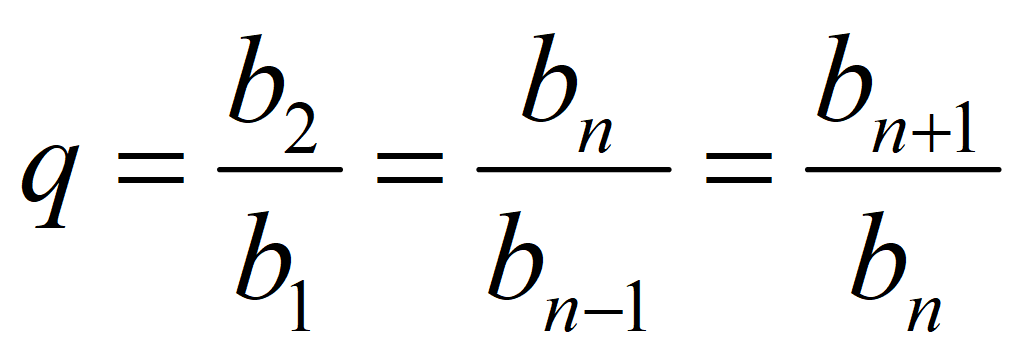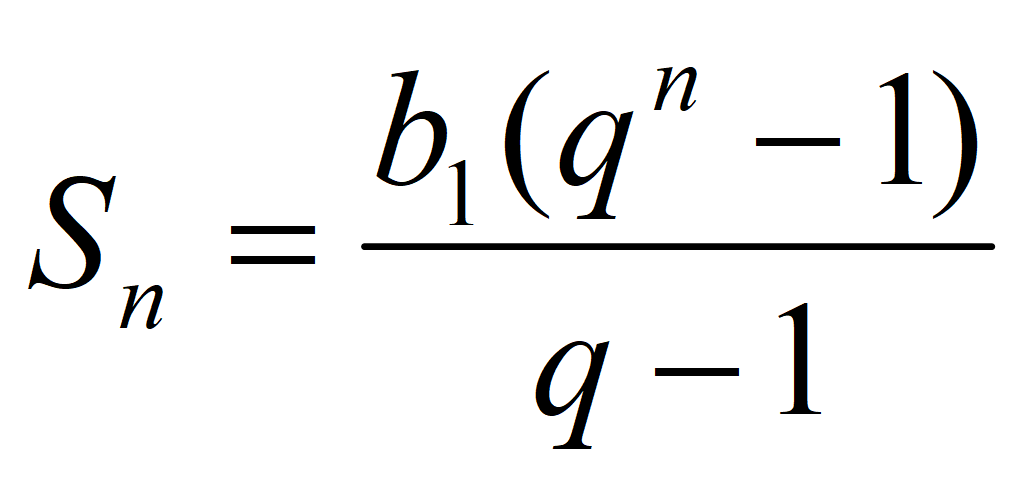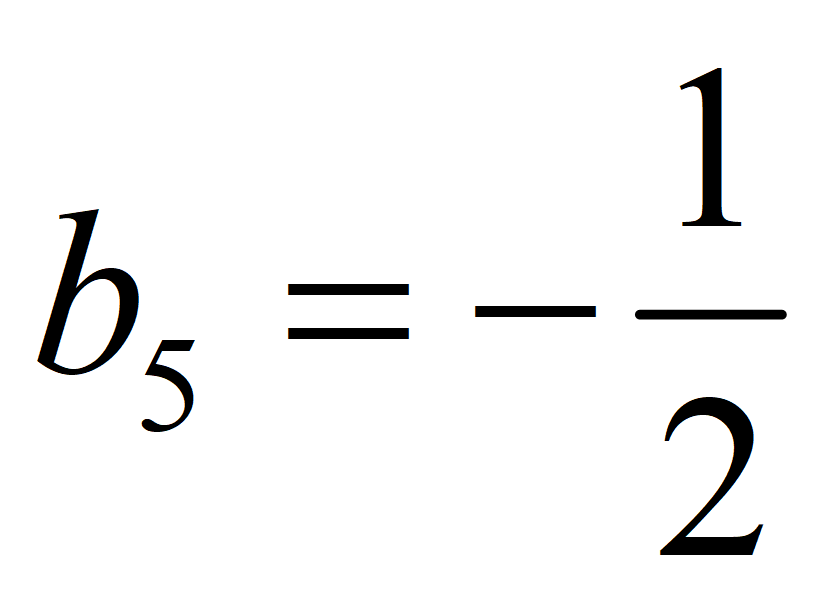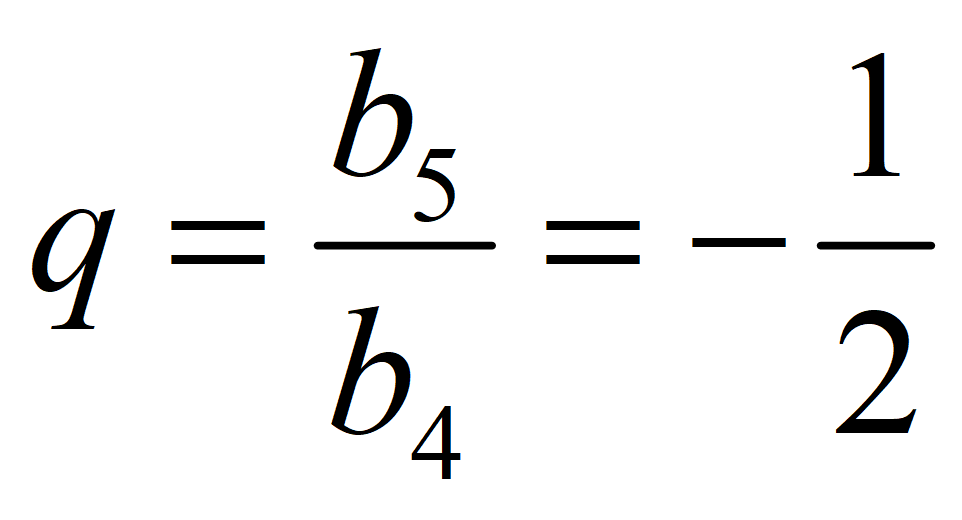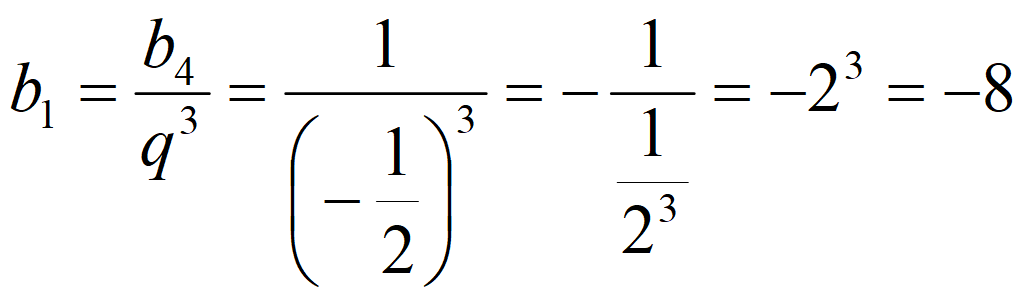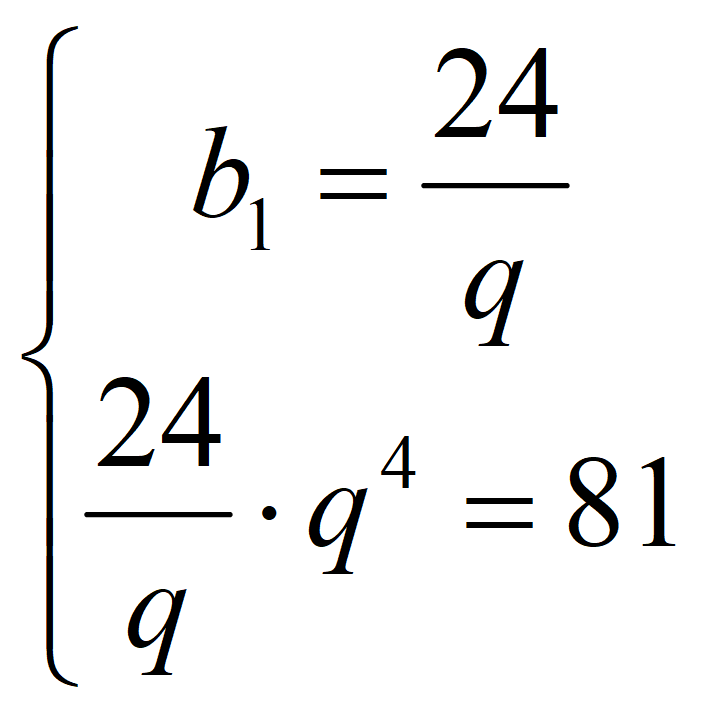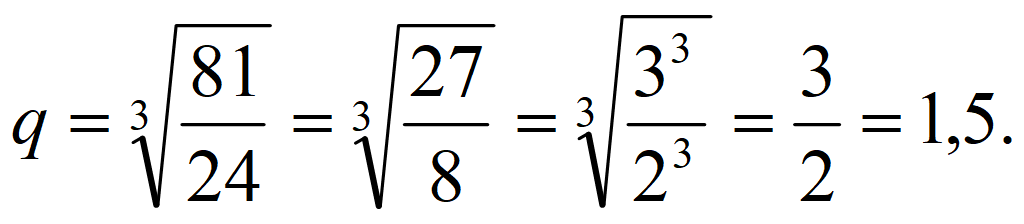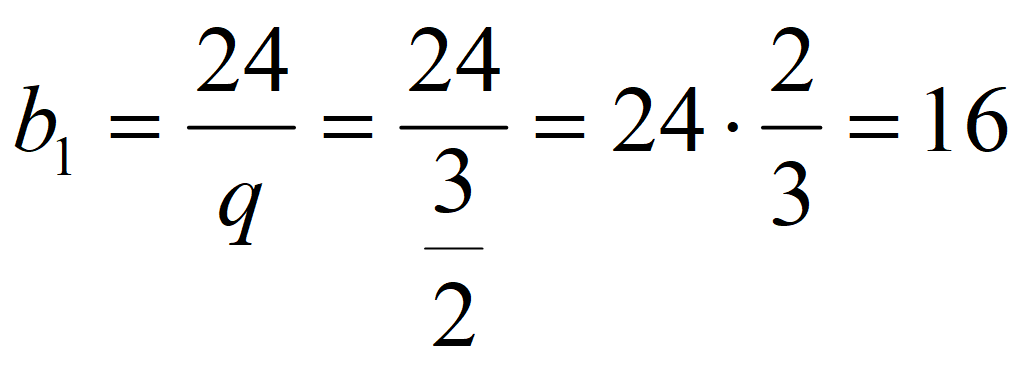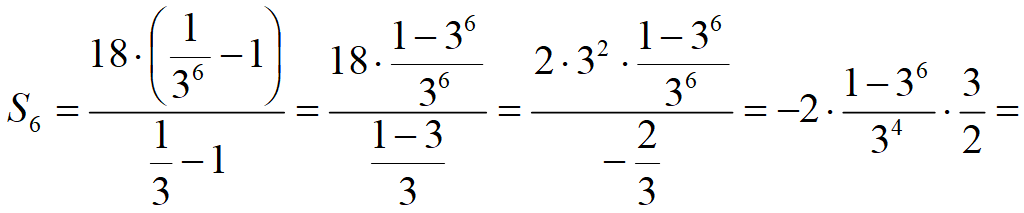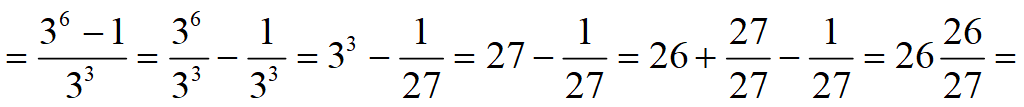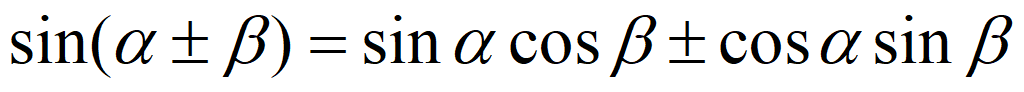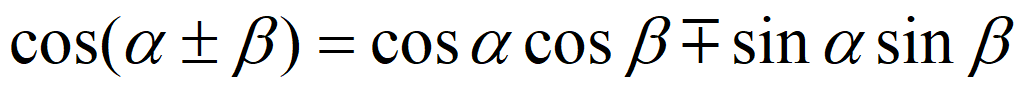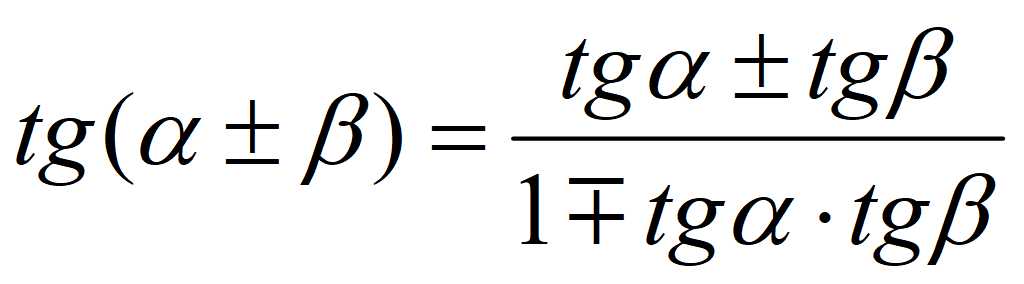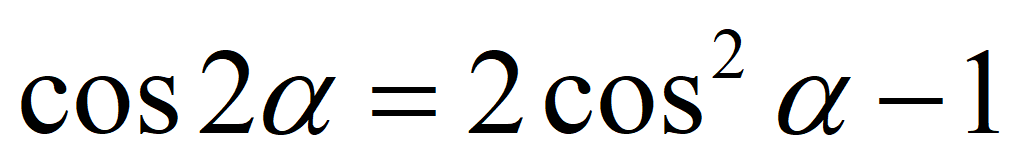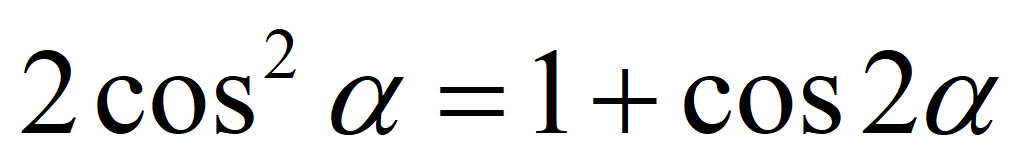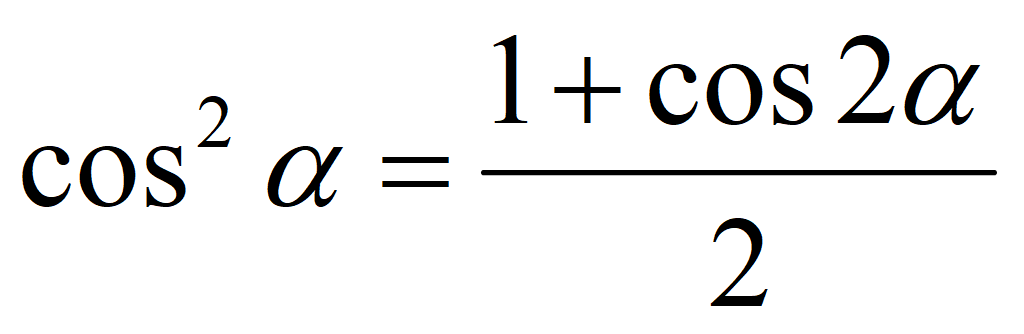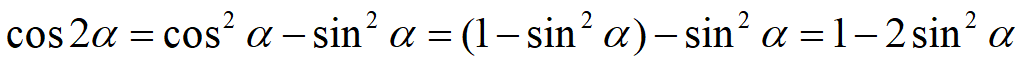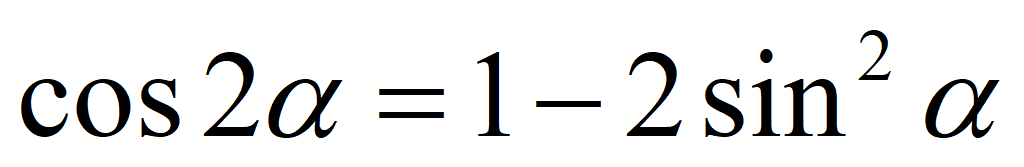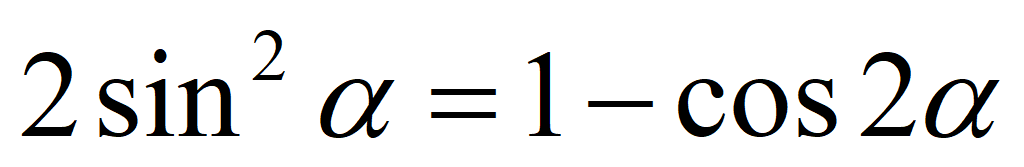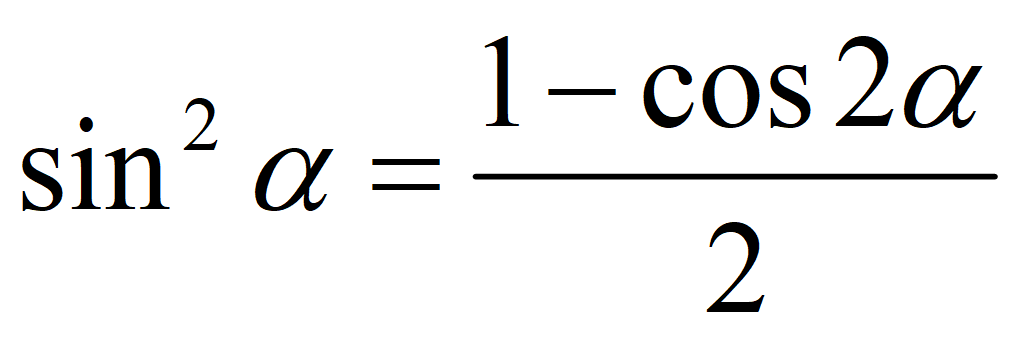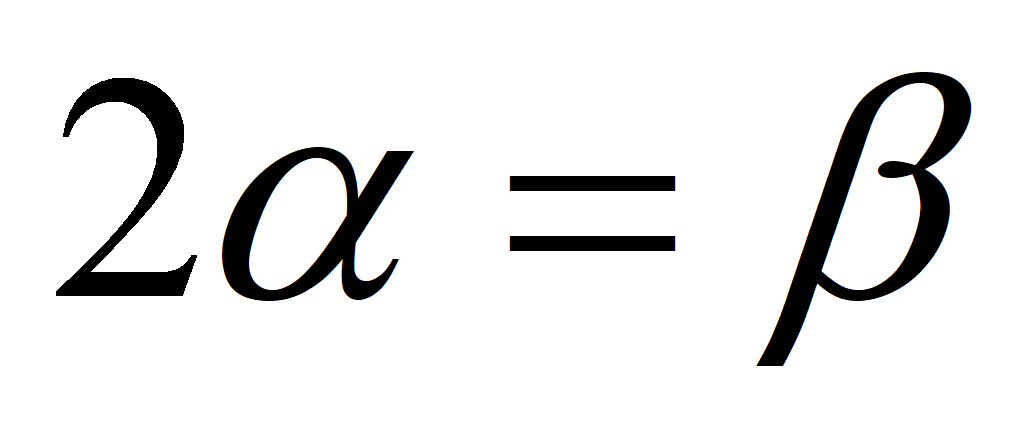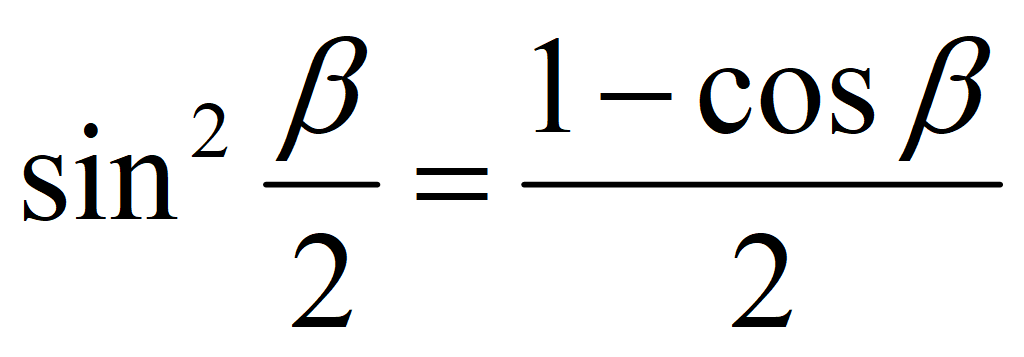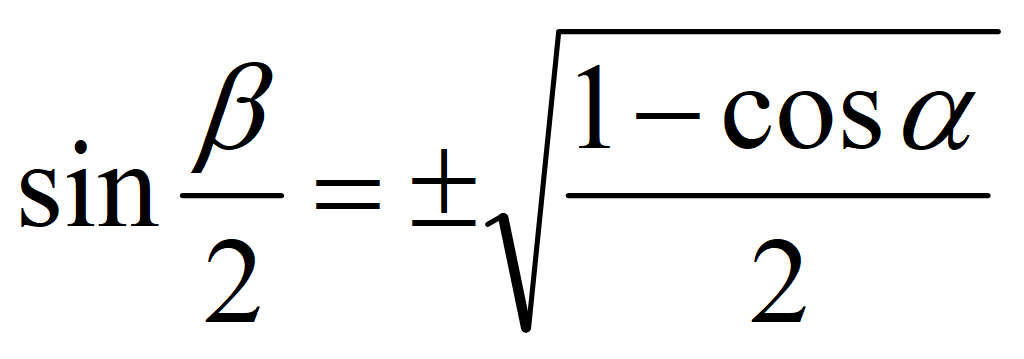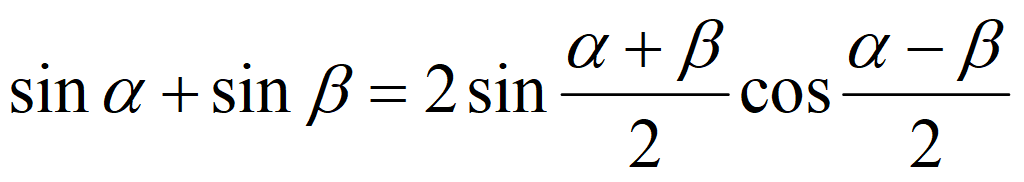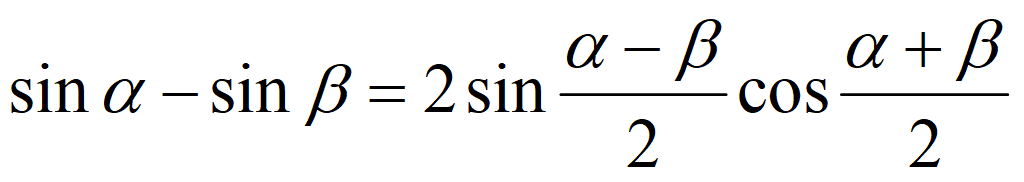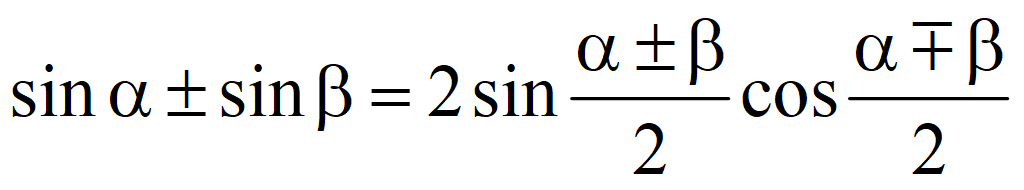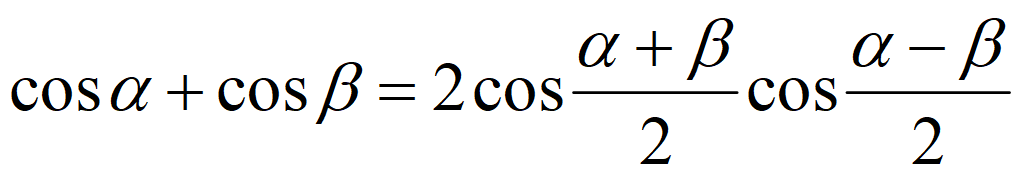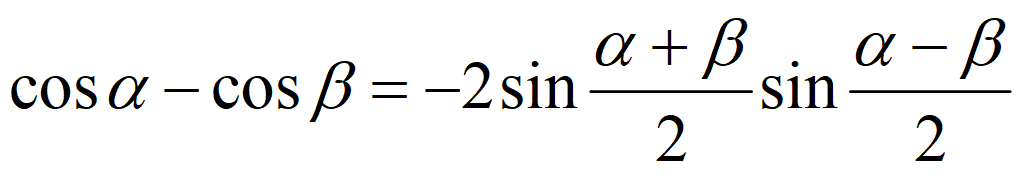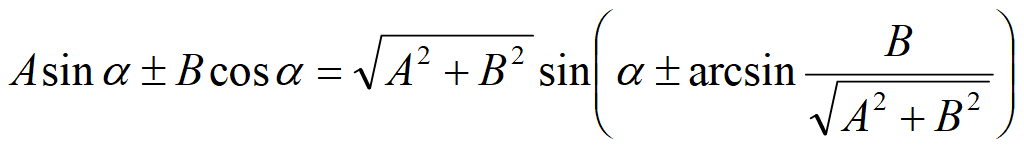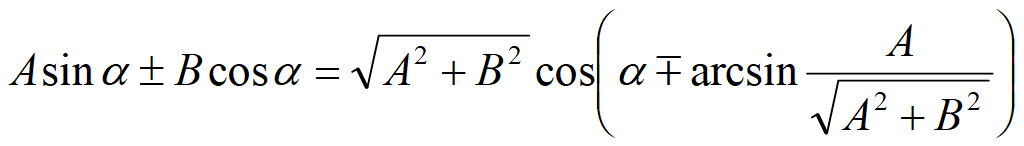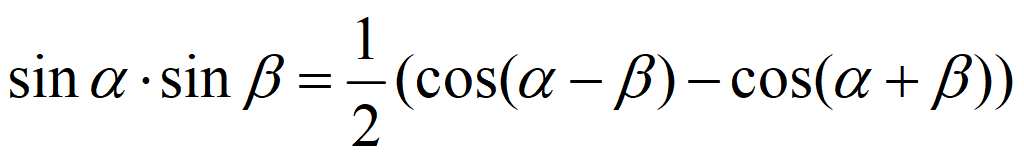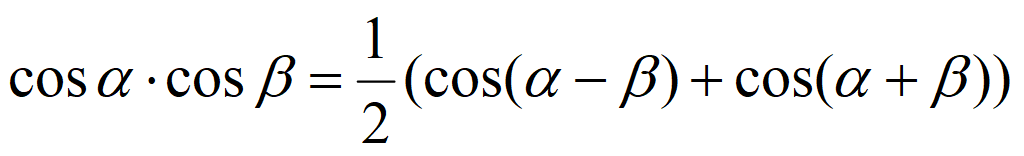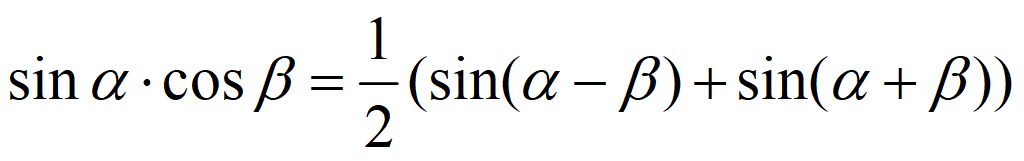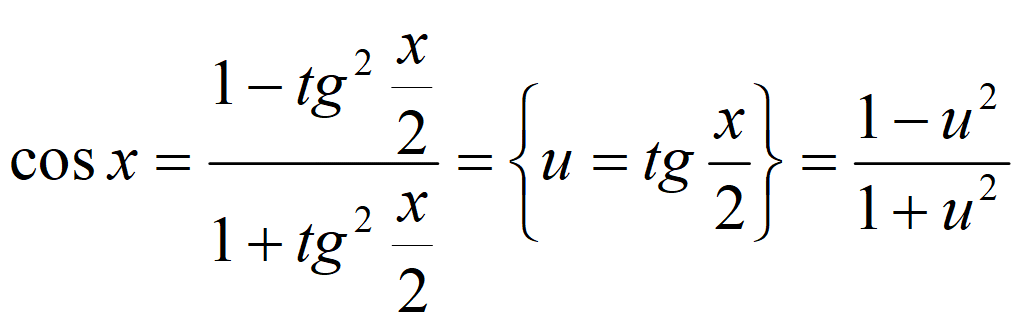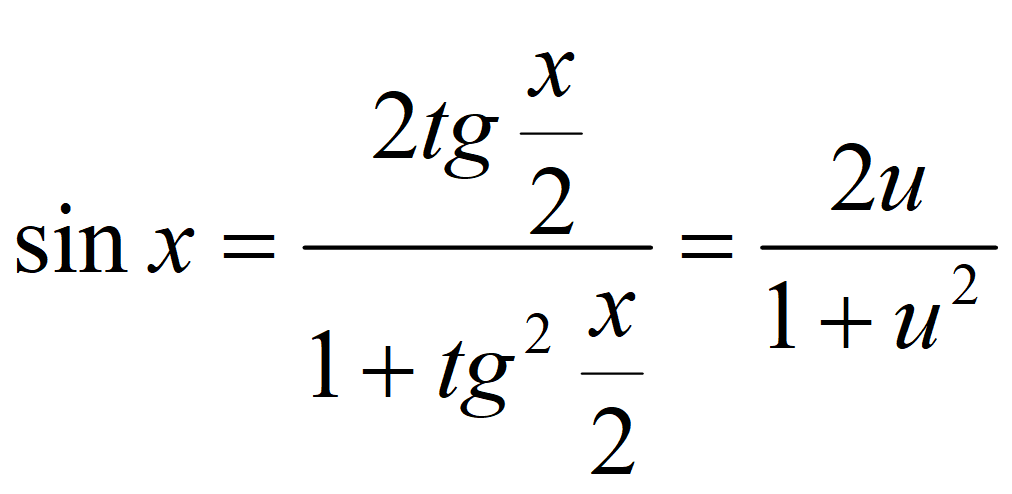Что такое объем в алгебре 7 класс

Презентация по алгебре «Данные и ряды данных 7 класс»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Элементы статистической обработки данных «Алгебра 7 класс» Мордкович А.Г. ( ФГОС) Учитель математики Леонова А.А. МБОУ «СОШ № 64» г. Барнаул

Цели урока : Познакомить с понятием статистика, математическая статистика; Узнать что изучает статистика; Узнать что такое ряд, объем ряда, размах ряда, мода, медиана ряда и среднее арифметическое ряда. Научиться находить объем ряда, размах ряда, мода, медиана ряда и среднее арифметическое ряда.

Статистика — это точная наука, изучающая методы сбора, анализа и обработки данных, которые описывают массовые действия, явления и процессы Математическая статистика – это раздел математики, изучающий методы сбора, систематизации и обработки результатов наблюдений случайных массовых явлений с целью выявления существующих закономерностей.

Статистика изучает: численность отдельных групп населения страны и ее регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и многое другое.

Результаты статистических исследований широко используются для практических и научных выводов. В настоящее время статистика начинает изучаться уже в средней школе, в ВУЗах это обязательный предмет, потому что связан со многими науками и отраслями. Чтобы увеличить количество продаж в магазине, чтобы улучшить качество знаний в школе, чтобы двигать страну по экономическому росту, надо проводить статистические исследования и делать соответствующие выводы. И это должен уметь каждый.

Главные цели изучения элементов статистики Формирование умений первичной обработки статистических данных; изображение и анализ количественной информации, представленной в разных формах (в виде таблиц, диаграмм, графиков реальной зависимостей); формирование представлений о важных статистических идеях, а именно: идее оценивания и идее проверки статистических гипотез; формирование умений сравнивать вероятности наступления случайных событий с результатами конкретных экспериментов.

Содержание Ряд данных Объем ряда данных Размах ряда данных Мода ряда данных Медиана ряда Среднее арифметическое

Определение Ряд данных – это ряд результатов каких-либо измерений. Например:1) измерения роста человека 2) Измерения веса человека (животного) 3)Показания счетчика (электроэнергии, воды, тепла…) 4) Результаты в беге на стометровку И т.д.

Задание из задачника (приложение) «Данные и ряды данных». П.1 Устно решите уравнения: 2x = –4; 4x = 25 – x; 17 + x = 8; 3 (x + 2) – 2 = x; 3 – x = 4 – (1 – 3x); 16 –x = 2x + 1; –4x – 8 = 0; 12x – 11 = –11(x + 1); 1–x = 6 – 2x; – 2 – (3 – x) = – 7.

Результат : Объем б) Объем ряда : 10

Результат : Размах в) Размах : 14

Определение Модой ряда данных называется число ряда, которое встречается в этом ряду наиболее часто. (Если таких элементов нет, то моды у данного ряда нет)

Чему равна медиана ряда? Так как объем нашего ряда число четное, то медиана : ( 0 + 5) : 2 = 2,5.

Среднее арифметическое ряда? (– 2 + 5 + (– 9) +(– 2) + 0 + 5 + (– 2) + 0 + 5 + (– 2)): 10 = –2 : 10 = – 0,2 Среднее арифметическое ряда : – 0,2

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-713123

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Более 50 российских школ перешли на дистанционку из-за коронавируса

Время чтения: 1 минута

Онлайн-конференция о профориентации и перспективах рынка труда

Время чтения: 3 минуты

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

В Москве новогодние каникулы в школах могут начаться с 27 декабря

Время чтения: 1 минута

Совфед отклонил закон о верифицированных онлайн-платформах и учебниках

Время чтения: 2 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Что такое объем в алгебре 7 класс

Выражения и их преобразования

☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а: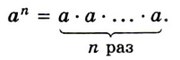
Степенью числа а с показателем 1 называют само число а: а 1 = а.
Степень числа а ≠ 0 с показателем 0 равна 1: а 0 = 1.

☑ 2. Свойства степеней с натуральными показателями:

а m • а n = а m+n

При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.

(а m ) n = а mn

При возведении степени в степень основание оставляют прежним, а показатели перемножают.

(ab) n = а n b n

При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.

Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена –8а 2 b 4 равна 6.

☑ 4. Многочленом называют сумму одночленов. Например, 3х 5 – 4х 2 + 1, 7a 3 b – ab 2 + ab + 6 —многочлены. Одночлены считают многочленами, состоящими из одного члена.

Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х 3 у + 3х 2 у 5 + ху равна степени одночлена 3х 2 у 5 , т. е. равна 7.

Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.

☑ 5. При сложении многочленов пользуются правилом раскрытия скобок : если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,

(3аb + 5с 2 ) + (ab – с 2 ) = 3ab + 5с 2 + ab – с 2 = 4аb + 4с 2

При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,

(6x 2 – у) – (2x 2 – 8у) = 6х 2 – у – 2х 2 + 8у = 4х 2 + 7у

Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например,

а 2 (3аb – b 3 + 1) = 3а 3 b – а 2 b 3 + а 2

Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,

(5х – 1)(3х + 2) = 15x 2 – Зx + 10x – 2 = 15x 2 + 7x – 2

☑ 6. Формулы сокращённого умножения:

(а + b) 2 = а 2 + 2аb + b 2

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

(а – b) 2 = а 2 – 2аb + b 2

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

(а + b) 3 = а 3 + 3а 2 b + 3ab 2 + b 3

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(а – b) 3 = а 3 – 3а 2 b + Заb 2 – b 3

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(а – b)(а + b) = а 2 – b 2

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

а 3 + b 3 = (а + b)(a 2 – аb + b 2 )

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

а 3 – b 3 = (а – b)(a 2 + ab + b 2 )

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.

Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен 5х 3 – х 2 у можно разложить на множители, вынеся за скобки х 2 :

Многочлен 3х – 3у – ах + ау можно разложить на множители, используя способ группировки:

3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).

Многочлен а 4 – 25x 2 можно разложить на множители, используя формулу разности квадратов двух выражений:

а 4 – 25x 2 = (а 2 ) 2 – (5x) 2 = (а 2 – 5x)(а 2 + 5x).

Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.

Алгебра 7 класс Все формулы

Уравнения

Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.

☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x 2 = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными.

При решении уравнений с одной переменной используются следующие свойства:

Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 7 не имеет корней.

Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.

Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.

В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному.

☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.

☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.

Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.

☑ 14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = –1 — решение системы
так как является верным каждое из равенств 7 + (–1) = 6 и 2 • 7 – (–1) = 15.

Решить систему уравнений — значит найти все её решения или доказать, что решений нет.

Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными.

☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.

При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:

При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:

При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:

Алгебра 7 класс Все формулы

Функции

Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.

Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.

Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью.

График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k у = х 2 — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.

График функции у = х 3 проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.

Статистические характеристики

☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых.

Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем.

Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине.

Например, медиана ряда чисел 17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел 28, 43, 54, 56, 58, 62 равна 55.

Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда.

Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел.

Вы смотрели Конспект «Алгебра 7 класс Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия:

Источник

§ 11. Основные понятия (продолжение)

Пару значений (х; у), которая одновременно является решением и первого, и второго уравнений системы, называют решением системы.

Решить систему — это значит найти все её решения или установить, что их нет.

Теперь мы можем сказать, что встречались с системой линейных уравнений — математическая модель уже упомянутой задачи про садоводов из § 7 выглядела так:

Её решением была пара (2; 5), т. е. х = 2, у = 5.

Рассмотрим новые примеры.

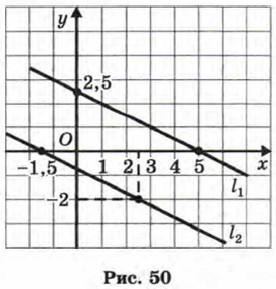
Пример 1. Решить систему уравнений

Прямые l₁ и l₂ параллельны. Что означает этот геометрический факт для данной системы уравнений? То, что она не имеет решений (поскольку нет точек, удовлетворяющих одновременно и тому и другому уравнению, т. е. принадлежащих одновременно и той и другой из построенных прямых l₁ и l₂).

О т в е т: система не имеет решений.

Замечание. Если бы мы с самого начала догадались переписать 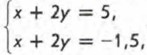то сразу было бы очевидно, что решений нет (и соответствующие прямые на самом деле параллельны).

Пример 2. Найти два числа, если известно, что их сумма равна 39, а разность равна 11.

Получили систему двух линейных уравнений с двумя переменными. Можно угадать, чему равны х и у: х = 25, у = 14. Но, во-первых, «метод угадывания» далеко не всегда применим на практике. А во-вторых, где гарантия, что иного решения нет, может быть, мы просто до него не додумались?

Источник

7 класс

Линейное уравнение с двумя переменными

Решением уравнения с двумя переменными, например ax + by + c = 0, называют пару чисел ( x ; y ), удовлетворяющих этому уравнению, то есть дающих верное числовое равенство при подстановке решения в заданное уравнение.

Задача. Найти два решения уравнения 2 x + 5 y + 7 = 0 и построить график функции

Алгоритм нахождения решения линейного уравнения с двумя переменными ax + by + c =0

1.Выразить переменную y через переменную x

2.Задать конкретное значение переменной x = x ₁; найти значение y = y ₁

Алгоритм построения графика линейного уравнения с двумя переменными ax + by + c =0

1.Выразить переменную y через переменную x

2.Задать конкретное значение переменной x = x ₁; найти значение y = y ₁

3.Задать другое конкретное значение переменной x = x ₂; найти значение y = y ₂

5.Через эти две точки провести прямую, которая и является графиком линейного уравнения ax + by + c = 0.

Выразить переменную y через переменную x

Задача. Построить график функции ax + by + c = 0 при a = 1, b = 1 и c = 1

Это уравнение линейной функции, поэтому для построения графика функции достаточно двух точек

Формулы сокращенного умножения

Сумма кубов a 3 + b 3 = (a + b)(a 2 – ab + b 2 ).

8 класс

9 класс

Числовая функция

Область определения функции

Задание функции y = f ( x ) на области определения X или D ( f )

Область значений функции

Способы задания функции

Основные способы задания фунций:

1.Аналитический – функция y = f ( x ) задается формулой (формулами).

Четные и нечетные функции

Для четной функции f ( x ), x ϵ X выполняется равенство

для нечетной функции f ( x ), x ϵ X выполняется равенство

Область определения D ( f ) четной или нечетной функции y = f ( x ) является симметричным множеством.

Если область определения D ( f ) не является симметричным множеством или условия четности и нечетности функции f ( x ) не выполняются, то функция ни четная, ни нечетная.

Законы сложения

2.Распределительный закон ( a + b ) + c = a + ( b + c ).

2.Сочетательный закон ( ab ) c = a ( bc ).

Числовая последовательность

График числовой последовательности представляет из себя набор точек с натуральным аргументом и значениями функции, вычисленными в этих точках.

Аналитический способ задания числовой последовательности

Словесный способ задания последовательности

При словесном способе правило составления последовательности описывается словами, а не формулой.

Рекуррентный способ задания последовательности

Например, последовательность y ₁ = 2; y _n = y _{n -1} + 3, при n > 1 задана рекуррентно.

Арифметическая прогрессия

Арифметическая прогрессия задается рекуррентно:

где первый член a ₁ и разность арифметической прогрессии d – заданны числами;

a _n – член прогрессии, начиная со второго;

a _{n -1} – предыдущий член арифметической прогрессии.

n – ный член арифметической прогрессии

Сумма n членов арифметической прогрессии:

Подставим a _n = a ₁ + (n – 1)d

Подставляем в заданную систему

и получаем систему уравнений

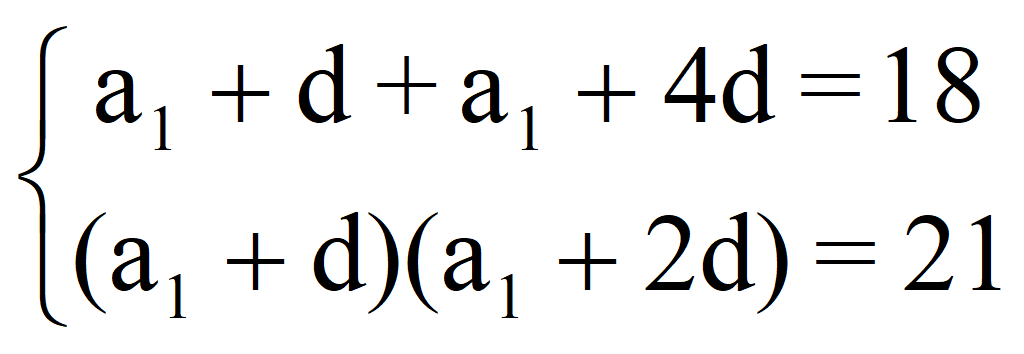
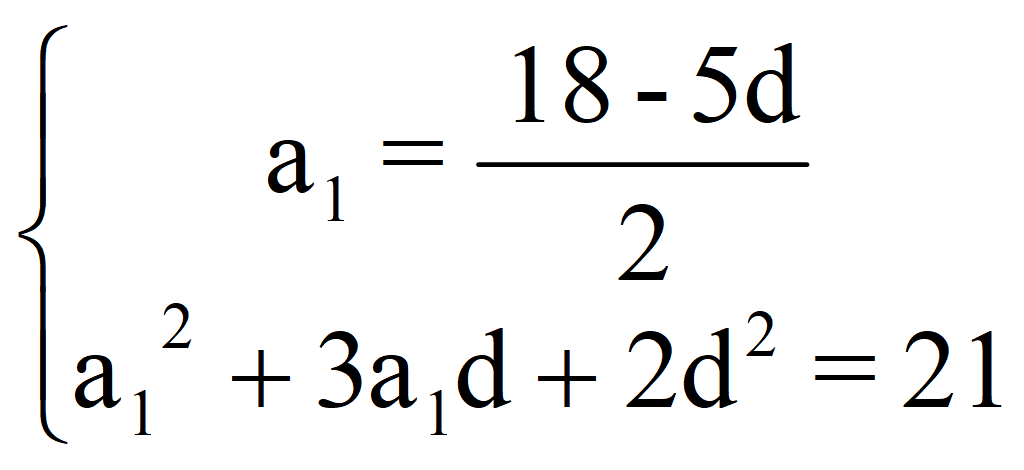
81 – 45 d + 6,25 d 2 + 27 d – 7,5 d 2 + 2 d 2 = 21;

0,75 d 2 – 18 d + 81 – 21 = 0;

0,75 d 2 – 18 d + 60 = 0.

Разделим на 0,75, то есть умножим на 4/3

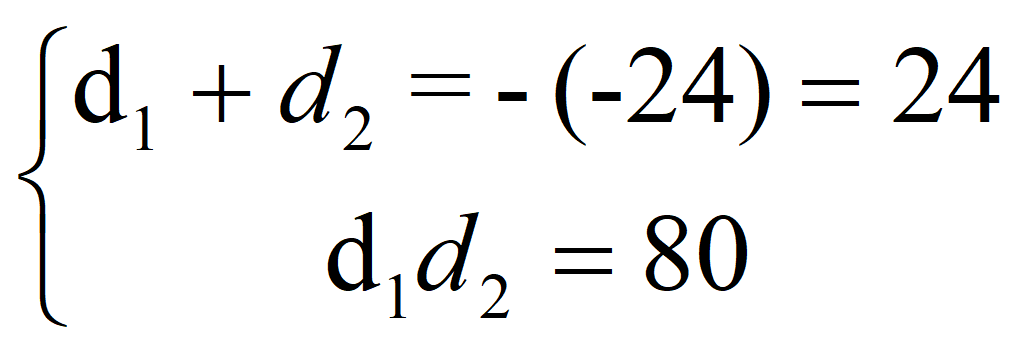
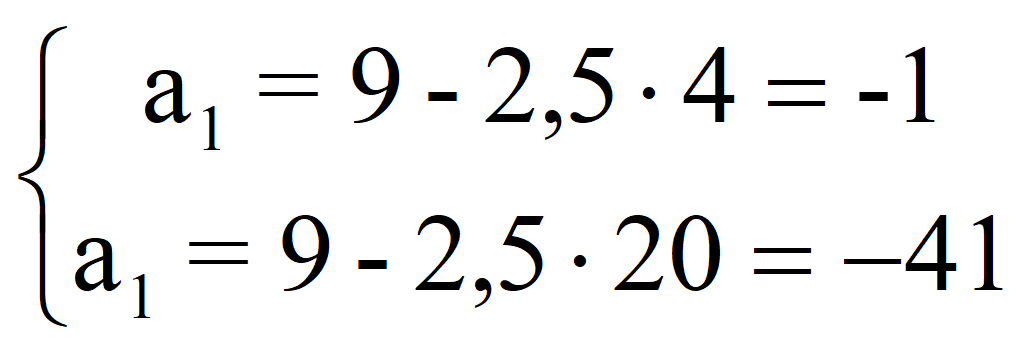
Геометрическая прогрессия

Геометрическая прогрессия задается рекуррентно:

где первый член b ₁ и знаменатель геометрической прогрессии q – заданны числами;

b _n – член прогрессии, начиная со второго;

b _{n -1} – предыдущий член арифметической прогрессии.

Знаменатель геометрической прогрессии

Задача 17.12 (б) [Мордкович. Задачник 9 класс]

Найдите b ₁ и q для геометрической прогрессии ( b _n ), заданной следующими условиями:

b ₄ = 1,

Знаменатель геометрической прогрессии

Формула 4-го члена геометрической прогрессии:

Задача 17.22 (б) [Мордкович. Задачник 9 класс]

Найдите b ₁ и q для геометрической прогрессии ( b _n ), заданной следующими условиями:

Знаменатель геометрической прогрессии

Формула 2-го члена геометрической прогрессии:

Формула 5-го члена геометрической прогрессии:

Получаем систему уравнений

;

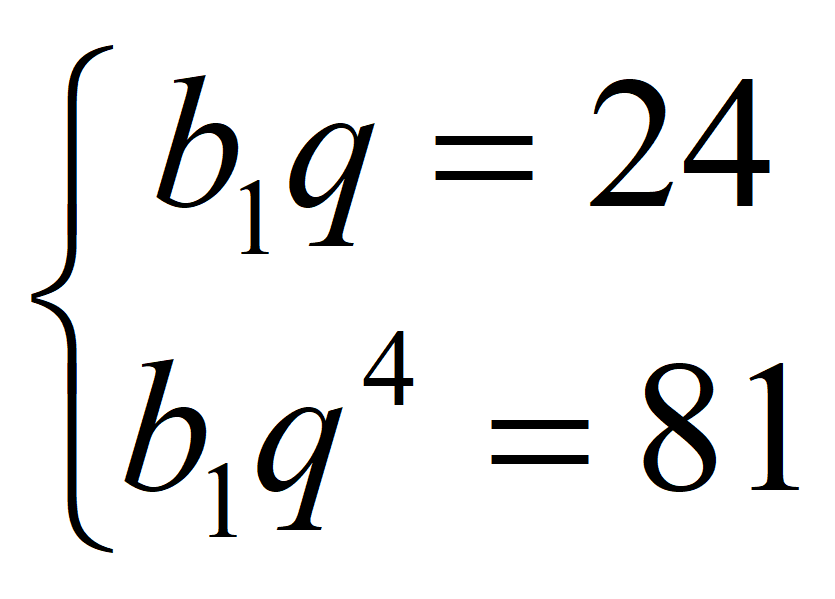
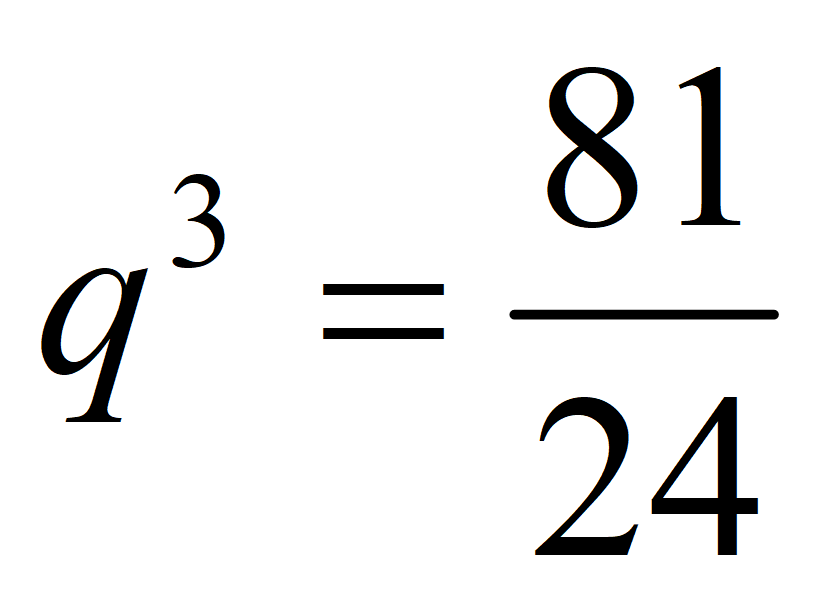
10 класс

Признак делимости на 11

Признак делимости на 7 или 13

Натуральное число делится на 7 или 13, если алгебраическая сумма чисел

Простые и составные числа

Составным называется число, имеющее больше двух делителей.

Число 1 не является ни простым, ни составным, так как делится лишь на 1.

Произвольное натуральное число, большее 1 имеет как минимум один простой делитель.

Множество простых чисел бесконечно [10].

Расстояние между двумя соседними простыми числами может быть больше любого наперед заданного натурального числа [10].

Обратные тригонометрические функции

Тригонометрические формулы

Сложение и вычитание аргументов

Формулы двойного угла

sin 2 α = 2 sinαcosα

Формулы понижения степени

Сложение и вычитание функций

Преобразование произведения в сумму и разность

Методы решения тригонометрических уравнений

Приравнять к нулю и разбить на множители

Подстановка

Универсальная тригонометрическая подстановка

11 класс

Многочлены от одной переменной

Стандартным видом многочлена p ( x ) является расположение его одночленов по убыванию степеней его одночленов

Два многочлена равны, когда они имеют одинаковые коэффициенты при одинаковых степенях переменной.

Если многочлен p ( x ) делится на многочлен q ( x ), то в результате получается многочлен s ( x ).

Если многочлен p ( x ) не делится на многочлен q ( x ), то в результате получается многочлен s ( x ) плюс остаток r ( x ), степень которого меньше степени многочлена q ( x ).

Вы можете поддержать развитие сайта с помощью платежной формы ниже.

Также Вы можете оплатить консультационные и прочие услуги Ольшевского Андрея Георгиевича

Источник