Что такое область фигуры

Что такое область фигуры

Введем некоторые определения, которые понадобятся в дальнейшем.

Определение. Областью (открытой областью) называется множество точек плоскости, обладающее следующими двумя свойствами:

1) каждая точка области принадлежит ей вместе с некоторой окрестностью этой точки (свойство открытости);

2) всякие две точки области можно соединить непрерывной линией, целиком лежащей в этой области (свойство связности).

Часть плоскости, лежащая внутри замкнутого контура L (рис. 216), является областью, так как; 1) для любой точки Р, лежащей внутри L, существует окрестность, также лежащая внутри L; 2) две любые точки Р и Q, лежащие внутри L, можно соединить непрерывной кривой, лежащей внутри

Области определения функций в примерах 1 и 3 п. 1 являются открытыми областями. Вся плоскость, очевидно, также является открытой областью.

Точка называется граничной точкой области G, если любая окрестность этой точки содержит как точки области G, так и точки, ей не принадлежащие.

Множество всех граничных точек области называется ее границей.

На рис. 216 любая точка контура, очевидно, является граничной.

Границу области на рис. 211 составляют неотрицательные части осей

Если к открытой области присоединить ее границу, то полученное множество точек называется замкнутой областью.

Области определения функций в примерах 2 и 4 (см. рис. 212 и 213) являются замкнутыми.

Если для данной области можно подобрать круг, полностью ее покрывающий, т. е. такой, внутри которого лежат все точки области, то такая область называется ограниченной.

Если же круга, полностью покрывающего область, подобрать нельзя, то область называется неограниченной. Ограниченными областями являются области определения функций, рассмотренные в примерах 2, 3 и 4 § 1 п. 1 (см. рис. 212, 213). Напротив, область определения функции в примере — неограниченная область. Область G (открытая или замкнутая) называется односвязной, если для любого замкнутого контура, лежащего в этой области, ограниченная им часть плоскости целиком принадлежит области G. Области, изображенные на рис. 211, 212, являются, очевидно, односвязными. Напротив, область, заключенная между окружностями (см. рис. 213), не является односвязной, так как, например, окружность лежащая в этой области, содержит внутри себя точки, не принадлежащие области (например, начало координат).

Замечание. Все введенные в этом пункте понятия почти без изменений переносятся на пространство трех и большего числа измерений.

Источник

Области и границы

1. Мотивация к учебной деятельности.

Организация учебного процесса на этапе 1:

— Ребята, назовите столицу нашей Родины. (Москва)
— Назовите столицу нашей республики (Нальчик)
— А какие города нашей республики ещё вы знаете?
— Сегодня мы совершим путешествие и узнаем, какие еще есть соседи у нашей столицы. Но путешествие будет не из легких. Вам предстоит узнать что-то новое. Готовы ли вы к этому? (Да)
— Какие основные шаги вы должны сделать при изучении нового? (Самим понять, что мы не знаем, и постараться самим “открыть” новое знание)
— В путешествии нам пригодится тема, которую мы изучали на последнем уроке “открытия”. Что мы изучали? (Мы изучали виды линий)
— Перед тем, как отправиться в путь, проверим свою готовность.

2. Актуализация знаний и фиксация индивидуального затруднения в пробном действии.

Организация учебного процесса на этапе 2:

— Сначала я предлагаю потренироваться в счете, играя в игру “День – ночь”.
— Итак, ночь.
— Учащиеся закрывают глаза и кладут головы на руки.
— К 1 прибавить 6, вычесть 2, прибавить 3, вычесть 4, прибавить 3, отнять 1. Какой ответ вы получили? (3)
— У кого другой ответ?
— Проверим, как вы считали.

2) Актуализация представлений о понятиях “точка” и “линия”, замкнутая и незамкнутая линии, способах обозначения точек.

Учитель открывает на доске задание №2

— Рассмотрите изображение. Какие фигуры вы видите? (Точки и линии)
— На какие группы можно разбить линии? (Замкнутые и незамкнутые)
— Какие линии называются замкнутыми? (Линии, в которых начало и конец совпадают)
— Какие линии называются не замкнутыми? (Линии, у которых есть начало и конец)
— Назовите точки. (А, К, Т.)
— Опишите расположение точек. (Точка А – внутри замкнутой линии, точка К – снаружи, точка Т – на незамкнутой линии)
— Нарисуйте листочках (листочки заранее лежат на столах) замкнутую линию красным карандашом, а незамкнутую – зеленым.

Учащиеся самостоятельно выполняют задание. Проверка организуется фронтально: учащиеся демонстрируют свои результаты на листах.

— Отметьте точку Б – внутри замкнутой линии, а точку М – на незамкнутой.

Учащиеся самостоятельно выполняют задание.

— Что вы видите на рисунке? (Замкнутую линию)
— Послушайте задание: попробуйте на этом рисунке красным цветом обозначить границу, а область – зеленым.
— Что нового в этом задании? (Мы не обозначали область и границу на рисунках)
— Какую цель мы поставим на уроке? (Научиться обозначать область и границу)
— Как назовем наш урок? (Область и граница)
— Попробуйте выполнить это задание.

Учащиеся самостоятельно выполняют пробное действие на карточках.

— Итак, у кого нет ответа?
— Что показало ваше пробное действие? (Мы не смогли найти на рисунке область и границу)
— У кого есть ответ?
— Кто может обосновать свои действия?
— Итак, что показало ваше пробное действие? (Мы не можем обосновать)
— Какой же наш следующий шаг на уроке? (Нужно подумать над нашим затруднением)

3. Выявление места и причины затруднения.

Цель: выявить и зафиксировать место и причину затруднения.

Организация учебного процесса на этапе 3:

— Какое задание вы выполняли? (Мы определяли на рисунке область и границу)
— Знакомы ли вам эти слова? (Да)
— В чем возникло затруднение?

4. Построение проекта выхода из затруднения.

Организация учебного процесса на этапе 4:

— Какую же цель мы перед собой поставим? (Открыть способ, с помощью которого мы могли бы определять область и границу и геометрических фигур)
— Давайте думать, что нам поможет. Куда мы должны были отправиться на уроке? (В путешествие)
— Верно, поэтому на урок я принесла карту.
— Учитель открывает на доске карту Кабардино-Балкарии
— Посмотрите на нее. Кто знает, что это за карта?
— Как она нам может помочь? (Мы можем на этой карте найти область и границу, и сделаем вывод)

Организация учебного процесса на этапе 5:

— Какой сейчас ваш шаг на уроке? (Попытаться сделать “открытие” самим)

(Можно рассмотреть карту Московской области в учебнике “Математика”).

— Для удобства карта Московской области дана в учебнике на странице 60.

Учащиеся открывают нужную страницу учебника.

— Что значит граница? (Это края области)
— Верно, другими словами это контур. Посмотрите внимательно, что напоминает граница? (Замкнутую линию)
— А где же область? (Область находится внутри границы)

— Какие города находятся в Московской области? (При работе по учебнику)
— Какие города находятся в Кабардино – Балкарии? (При работе с картой у доски)

Учащиеся перечисляют названия городов.

— Сначала мы обвели границу Московской области, то есть края. Московская область оказалась внутри. Наш вывод: граница – это край фигуры (контур), область – внутри фигуры.

Далее работа организуется фронтально.

— Вернемся к нашему заданию. Где же граница? (Это контур фигуры)
— Обведите границу красным карандашом.
— Что мы сейчас обозначили? (Границу)
— Где же находиться область? (Внутри границы)
— Раскрасьте область зеленым карандашом.
— Сделайте вывод.
-Что теперь мы можем? (Обозначать области и границы у любых фигур)
— Какой следующий шаг на уроке? (Закрепить новое знание)

6. Первичное закрепление с проговариванием во внешней речи.

Цель: зафиксировать новое учебное содержание во внешней речи.

Организация учебного процесса на этапе 6:

1) №2, стр. 60

— Найдите №2 на странице 60.

Учитель заранее выносит задание на доску.

— Обозначьте красным карандашом границу фигуры, а зеленым – область.
— Какие точки находятся в области? (Точки А, В.)
— Какие точки находятся на границе? (Точки М, К.)
— Опишите расположение точек Б, Д. (Точки Б, Д находятся снаружи области и ее границы)

— Найдите №4 на этой же странице.

— Итак, проверим ваши результаты.
— Кто допустил ошибку?
— В чем она? (Неправильно определили границу, …)
— Исправьте ошибки зеленым карандашом.
— Вы молодцы, так как нашли и исправили свои ошибки. Как проверить себя, что вы не допустите больше ошибок? (Нужно выполнить самостоятельную работу)

7. Самостоятельная работа с самопроверкой по эталону.

Организация учебного процесса на этапе 7:

— Найдите №3 на этой же странице.
— Обозначьте границу фигуры красным цветом, а область – желтым.

— Проверьте свою работу по образцу.
— Кто допустил ошибки?
— В чем они?
— Исправьте ошибки зеленым карандашом.
— Сделайте вывод. (Нужно еще потренироваться в определении области и границы)
— Кто выполнил самостоятельную работу без ошибок?
— Сделайте вывод. (Мы умеем определять области и границы у фигур)

8. Включение в систему знаний и повторение.

Цель: тренировать умение сравнивать группы предметов по количеству.

Организация учебного процесса на этапе 8:

— Во время любого путешествия нужно быть внимательными, нужно уметь наблюдать и делать выводы. Поэтому в конце урока я предлагаю потренировать в себе эти качества.

— Найдите №8 на странице 61.
— Какое задание нужно выполнить? (Составить и решить примеры с помощью рисунка)
— Рассмотрите первый рисунок. Какое действие нужно выполнить? (Вычитание)
— Что представляет целое? (Шесть треугольников)
— Что представляет часть? (2 треугольника)
— Чему равна неизвестная часть? (4 треугольника)

Далее работа проводиться аналогично.

9. Рефлексия учебной деятельности на уроке.

Организация учебного процесса на этапе 9:

— Какую цель ставили на уроке? (“Открыть” способ определения границы и области)
— Удалось ли достичь поставленной цели? Докажите.
— Кому из вас удалось сделать “открытие” самому?
— Оцените свою работу на уроке веселой или задумчивой рожицей. Если у вас не было ошибок или вы смогли преодолеть затруднение и можете двигаться дальше, выберете веселую “рожицу”, если еще возникают затруднения по данной теме, то выберете задумчивую “рожицу”.

Учитель делает вывод.

— Вы все сегодня хорошо потрудились, скажите друг другу спасибо.

Источник

Основные геометрические фигуры

Основные понятия

Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.

Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.

Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.

Обучение на курсах по математике поможет быстрее разобраться в видах и свойствах геометрических фигур.

Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Периметром принято называть сумму длин всех сторон многоугольника. Периметр обозначается заглавной латинской P.

Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.

Если все точки фигуры принадлежат одной плоскости, значит она является плоской.

Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.

Примеры объемных геометрических фигур:

Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.

Прямоугольник

Прямоугольник — параллелограмм, у которого все углы прямые.

Узнать площадь прямоугольника помогут следующие формулы:

Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.

Периметр прямоугольника — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Квадрат

Квадрат — это тот же прямоугольник, у которого все стороны равны.

Найти площадь квадрата легко:

Периметр квадрата — это длина стороны, умноженная на четыре.

P = 4 × a, где a — длина стороны.

Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.

Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.

Как найти площадь трапеции:

S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.

Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.

P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны

Ромб — это параллелограмм с равными сторонами.

Общие формулы расчета площади фигур:

Периметр ромба — это произведение длины стороны на четыре.

P = 4 × a, где a — длина стороны.

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Треугольник

Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.

Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.

S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.

S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.

S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.

P = 3 × a, где a — длина стороны.

Круг — это это часть плоскости, которая лежит внутри окружности.

Окружность — это граница круга.

Радиус окружности — это расстояние от центра окружности до любой точки на ней.

Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.

Формулы площади круга:

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Источник

Геометрические фигуры на плоскости

Геометрическая фигура называется плоской, если все тонки фигу­ры принадлежат одной плоскости.

Примером плоских геометрических фигур являются: прямая, от­резок, круг, различные многоугольники и др. Не являются плоски­ми такие фигуры, как шар, куб, цилиндр, пирамида и др.

На плоскости различают выпуклые и невыпуклые фигуры.

Геометрическая фигура называется выпуклой, если она целиком со­держит отрезок, концами которого служат любые две точки, принад­лежащие фигуре (рис. 54).

Примерами выпуклых фигур являются: круг, различные треу­гольники, квадрат. Точку, прямую, луч, отрезок, плоскость также считают выпуклыми фигурами.

Основными геометрическими фигурами на плоскости являются точка и прямая. Эти термины часто применяются даже в работе с дошкольниками. Необходимо своевременно научить детей узнавать эти фигуры, изображать их, понимать и правильно выполнять зада­ния.

Основные свойства точек и прямых раскрываются в аксиомах:

1. Существуют точки, принадлежащие и не принадлежащие пря­мой.

2. Через две различные точки можно провести единственную прямую.

3. Две различные прямые либо не пересекаются, либо пере­секаются в одной точке.

Дети, например, в процессе игр или рисования знакомятся с точкой, отрезком, различными линиями, выделяя из них прямую, кривую, ломаную, учатся распознавать некоторые их свойства.

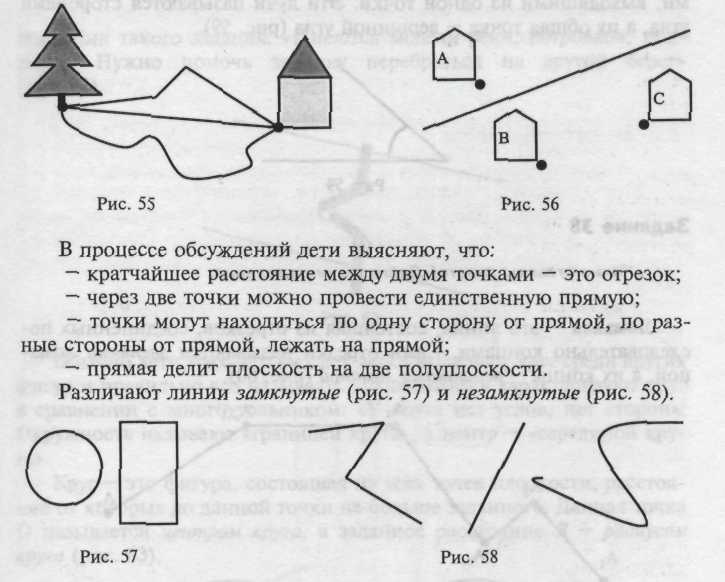
1. «Какая дорога от леса до дома короче?» (рис. 55).

2. «Поросята живут в домиках, расположенных на берегах реки. Они не умеют плавать. Кто из поросят может пойти в гости друг к другу?» (рис. 56).

Замкнутая линия делит плоскость на внешнюю и внутреннюю об­ласти. Дети рано усваивают, что значит «внутри» и «вне». Напри­мер, это происходит при выполнении задания на закрашивание фи­гуры, то есть ее внутренней области.

Геометрические фигуры, с которыми рано знакомятся дети (круг, квадрат, треугольник и др.), представляют собой замкнутые линии (границы фигур) с их внутренней областью. Границей круга

является окружность. Границей многоугольников является ломаная линия, которая состоит из отрезков. В геометрии все эти понятия имеют определения.

Отрезок — часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными точками, называемых кон­цами отрезка.

Луч (полупрямая) — это часть прямой, состоящая из всех ее то­чек, лежащих по одну сторону от заданной на ней точки (начала луча).

Круг можно определить как фигуру, состоящую из окружности и ее внутренней области.

Окружность — это множество точек плоскости, равноудаленных от заданной точки. Данная точка О называется центром окружнос­ти, а заданное расстояние R — ее радиусом (рис. 64).

В детском саду дети также знакомятся с овалом («фигурой, похо­жей на круг тем, что у нее нет углов и сторон, но отличающейся от круга своей вытянутостью»). В геометрии такой термин не рассмат­ривается, но изучается эллипс. Его нецелесообразно предлагать де­тям из-за сложности построения. Так как в быту часто используют слова «овал», «предмет овальной формы», знания об овале необхо­димы детям как элемент сенсорного воспитания и речевого раз­вития.

Многоугольники

Многоугольник — часть плоскости, ограниченная простой за­мкнутой ломаной. Звенья ломаной называются сторонами много­угольника, а вершины — вершинами многоугольника. Границу много­угольника (простую замкнутую ломаную) также называют многоу­гольником.

В работе с дошкольниками обычно рассматриваются модели фигур из картона, пластмассы или дерева, предлагаются задания по рисованию многоугольников при помощи трафаретов и обводок, за­крашиванию фигур. В процессе этой деятельности дети знакомятся с названиями фигур, их структурой и некоторыми свойствами, ис­пользуют такие термины, как: граница фигуры, внутренняя область фигуры и др.

Выпуклый многоугольник лежит в одной полуплоскости от­носительно любой прямой, содержащей его сторону (рис. 65).

Источник