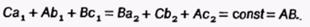Что такое область гомогенности

НЕСТЕХИОМЕТРИЯ

В границах области гомогенности равновесный состав в-ва является ф-цией т-ры и давления компонентов в сосуществующей фазе. Для полупроводниковых соед. связь между составом и указанными параметрами представляют в виде р-Т-Х-диаграмм (давление-т-ра-состав), из к-рых определяют условия синтеза кристаллов с желаемой величиной отклонения от стехиометрии. Обычно такие нестехиометрич. кристаллы получают, выдерживая их при заданных давлениях и т-ре до достижения равновесия, а затем резко их охлаждая для «закалки» желаемого уровня нестехиометрии. Величина области гомогенности и ее положение на диаграмме состояния зависят от т-ры, DG 0 обр в-ва-растворителя и величины изменения энергии Гиббса растворяющегося компонента при переходе его из самостоят. фазы в р-р.

Как правило, возникновение нестехиометрии сопровождается окислит.-восстановит. процессами, хотя нередки случаи растворения в осн. в-ве нейтральных частиц. В кристаллич. соед. d-элементов явления нестехиометрии часто влекут за собой изменение степени окисления атомов. Так, напр., при растворении в FeO избыточного кислорода эквивалентная ему часть атомов Fe(II) переходит в состояние Fe(III). В оксидных бронзах удаление из соответствующей подрешетки части ионов щелочного или др. электроположит. металла сопровождается эквивалентным изменением степени окисления переходного металла. Избыточные частицы в кристалле м. б. распределены статистически равномерно и не взаимод. друг с другом или же объединены в ассоциаты. В двухкомпонентных нестехиометрич. соед. в таких ассоциатах обычно насчитывается от неск. частиц до неск. десятков.

Область гомогенности может включать или не включать стехиометрич. состав. Обычно нестехиометрич. фазы, область гомогенности к-рых включает в себя стехиометрич. состав, относят к д а л ь т о н и д а м, а не включающие его-к б е р т о л л и д а м. Впервые такое разделение нестехиометрич. фаз ввел Н. С. Курнаков, имея в виду прежде всего то обстоятельство, что в пределах области гомогенности св-ва дальтонидов при изменении состава меняются не монотонно, а проходят через экстремальные значения, к-рым на диаграммах состояния отвечают особые (с и н г у л я р н ы е) точки. Курнаков назвал их дальтоновскими, поскольку состав соед. в этих точках удовлетворяет требованиям кратных отношений закона, впервые сформулированного Дж. Дальтоном. В отличие от дальтонидов св-ва бертолли-дов, названные так в честь К. Бертолле, в пределах области гомогенности изменяются монотонно, а если и проходят через минимумы или максимумы (обычно слабовыраженные), то соответствующие им составы не подчиняются правилам стехиометрии и сингулярные точки на них отсутствуют. Однако экстремальные значения нек-рых св-в далътонидов также не соответствуют стехиометрич. составу. В частности, положение минимума электрич. проводимости мн. нестехиометрич. оксидов и халькогенидов, отвечающего обычно изменению природы носителей зарядов, как правило, оказывается сдвинутым по отношению к стехиометрич. составу. Чаще всего такой сдвиг обусловлен тем, что носителями св-ва оказываются не сами избыточные против стехиометрии частицы, а продукты их взаимод. с кристаллом-дефекты.

Явления нестехиометрии всегда сопровождаются нарушением периодичности кристаллич. решетки и возникновением дефектов, с к-рыми связаны важнейшие св-ва нестехиометрич. кристаллов-электрофиз., оптич., магн., прочностные и др. Очень часто, напр., такие дефекты являются центрами окраски, что приводит к окрашиванию кристаллов, причем интенсивность окраски является ф-цией величины отклонения от стехиометрии. Так, при нарушении стехиометрии в сторону избытка металла кристаллы ВаО из бесцветных превращаются в голубые, NaCl-в желтые, КСl-в фиолетовые. На-триевольфрамовая бронза по мере удаления из нее Na меняет свой цвет от золотисто-желтого (NaWO 3 ) до темного сине-зеленого (Na 0,3 WO 3 ), проходя при этом через красный и фиолетовый цвета.

В ряде случаев возникновение дефектов стимулируют введением в кристалл посторонних примесей (активаторов). В таких случаях формирование св-в кристалла является результатом взаимод. дефектов, обусловленных как нестехиометрией, так и посторонними примесями. Т. обр., в частности, формируют фоточувствит. мишени видиконов на основе халькогенидов Cd (хальнеконы), получают нек-рые кристаллофосфоры. С нестехиометрией и вызванной ею дефектностью кристалла связаны явления переноса, в частности электрич. проводимость. К нестехиометрич. соед. относятся сверхпроводники.

Источник

Диаграммы П/П соединений

По способности растворять в себе ком­поненты соединения. Область твердых раство­ров компонентов на основе соединения назы­вают областью гомогенности соединения.

Далътониды — соединения с широкой областью гомогенности — характеризуются тем, что соединение формульного состава находится внутри области гомогенности (рис.10.13, а—в); общим для диаграмм с дальтонидными фазами является присутствие сингулярной точки на кривых ликвидуса и солидуса, состав в которой отвечает дальтониду и простым стехиометрическим соотноше­ниям компонентов. На диаграмме состав—свой­ство формульному составу соединения, как правило, соответствует экстремальное значе­ние ряда свойств.

Бертоллиды характеризуются тем, что соединение формульного состава лежит вне области гомогенности (рис. 10.13, г и д). Это означает, что соединение бертоллидного типа формульного состава не существует. Сплав, отвечающий формуле соединения, состоит из двух фаз, одна из которых представляет со­бой твердый раствор на основе соединения. Изобарно-изотермный потенциал этого твер­дого раствора меньше изобарно-изотермного потенциала соединения строго формульного состава. На диаграмме состав—свойство в пре­делах составов, отвечающих области гомоген­ности, свойства изменяются монотонно.

Несмотря на малую величину, раствори­мость играет важнейшую роль в формирова­нии физических свойств соединения. Поэтому изучение свойств твердых растворов, распо­ложенных в узкой области гомогенности (т. е. с избытком компонентов А и В), пред­ставляет собой важную и экспериментально сложную задачу.

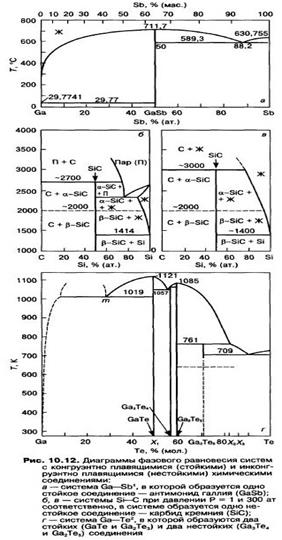
15) Диаграммы состояния систем с конгруэнтно плавящимися промежуточными фазами

Со­единения этого типа образуются во многих системах типа полупроводник—полупровод­ник, металл—полупроводник, металл—ме­талл.

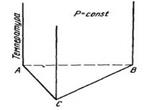
Промежуточные фазы, при плавлении которых составы жидкой и твердой фаз совпадают, называют конгруэнтно плавящимися (от лат. congruens— совпадающий, соответствующий).

Для диаграммы состояния с конгруэнтно плавящейся промежуточ­ной -фазой переменного состава (рис. 20, б) характерны сравнительно широкие области граничных а- и b-растворов и заметная растворимость компонентов А и В в соединении А_тВ_n, лежащем в основе у-фазы. В результате промежуточная -фаза имеет свою область гомогенности b₁bm’cc₁(на рис. 20, б эта область заштрихована).

16) Промежуточные фазы, при плавлении которых состав жидкой фазы отличается от состава твердой фазы, называют инконгруэнтно плавя­щимися (от лат. incongruens — несовпадающий, несоответствующий). При плавлении таких фаз помимо жидкости образуется новая твердая фаза, состав которой также отличается от состава плавящейся фазы. Иначе говоря, плавление инконгруэнтно плавящейся фазы происходит по реакции, обратной перитектической.

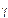
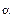
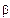
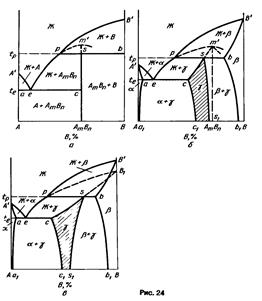
Если инконгруэнтно плавящаяся промежуточная -фаза имеет переменный состав и на основе компонентов А и В образуются гра­ничные — и -растворы, то характер диаграммы состояния такой

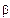
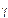
Инконгруэнтно плавящиеся промежуточные фазы называют также фазами со скрытым максимумом, подчеркивая, что на их кривых лик­видуса и солидуса нет точки максимума (дистектической точки). Скры­тый максимум m’ этих фаз можно показать пунктиром рm’ в двухфаз­ной области Ж + В (см. рис. 24, а) или рт’ и m’s в области Ж + (см.рис. 24, 6). В первом случае кривая рт’ изображает состав жидкости, находящейся в равновесии Ж = А_тВ_n а во втором кривые рт’ и sm’ — состав жидкости, находящейся в равновесии Ж = . Оба равновесия метастабильны и если бы реализовались, то должны были бы заме­ниться стабильными равновесиями Ж = В и Ж = р.

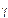
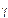
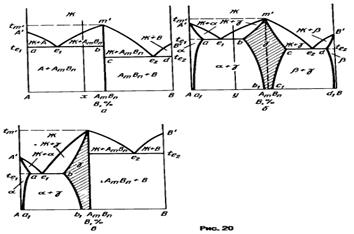
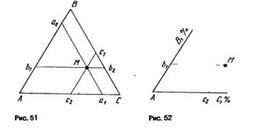
Из диаграммы состояния (см. рис. 24, а) видно, что скрытый мак­симум т’ отвечает составу соединения А_тВ_n Если промежуточная у-фаза имеет переменный состав (см. рис. 24, б), то этот максимум может оказаться за пределами области гомогенности у-фазы. Кроме того, состав соединения А_тВ_n не отвечает точке s на перитектической горизонтали pb, хотя эта точка изображает состав промежуточной s-фазы, образующейся по перитектической реакции Ж_р+ Bb► s

17) Обычно для изображения составов тройных сплавов используют плоскость, ограниченную сторонами правильного (т.е. равностороннего) треугольника. В вершины такого концентрационного треугольника (рис. 51) помещают компоненты А, В и С, стороны АВ, ВС и АС служат для изображения составов двойных сплавов, а на плоскости изобража­ют составы тройных сплавов. В обоих случаях концентрации компо­нентов в сплавах обычно выражают в процентах (по массе или атом­ных) или долях (атомных или мольных) от единицы.

Если сторону концентрационного треугольника принять равной единице или 100 %, то с помощью отрезков Са₁ Аb₁ и Вс₁ (или Ва₂, Сb₂ и Ас₂) можно определить концентрацию каждого из компонентов в сплаве М

Также видно, что концентрация компонента С в сплаве М превышает концентрацию компонента В (фигуративная точка сплава находится ближе к вершине компонента С). Следовательно, концентрацию ком­понента С в сплаве М можно определить самыми большими отрезками Bс₁ или Ас₂, которые опять от вершин компонентов В и А «отклады­ваются» в сторону компонента С. Наконец, концентрацию компонен­та В можно определить отрезками Аb₁ или Сb₂, которые от вершин компонентов А и С «откладываются» в сторону компонента В.

Следует отметить, что первые три отрезка Ca₁, Bb₁ и Ас₁ «отклады­ваются» от вершин концентрационного треугольника в направлении, совпадающем с ходом часовой стрелки, а другие отрезки Ва₂, Сb₂ и Ас₂— в обратном направлении.

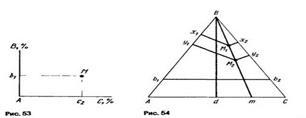
При отыскании фигуративной точки тройного сплава на плоскости концентрационного треугольника по его заданному химическому составу поступают следующим образом (рис. 52). От одной из вершин треугольника, например вершины компонента А, принятого за основу сплава, по сторонам АВ и АС откладывают отрезки Ab₁ и Ас₂, изме­ряющие концентрации компонентов В и С. Затем через точки b₁ и с₂ параллельно сторонам АВ и АС проводят прямые b₁М и С₂М, кото­рые пересекутся в фигуративной точке искомого сплава М.

Из рассмотренного свойства концентрационного треугольника (см. рис. 51) вытекает ряд особенностей состава разных групп тройных сплавов:

1. Все сплавы прямой, параллельной одной из сторон концентра­ционного треугольника, содержат постоянное количество того компо­нента, который находится в вершине треугольника против этой порямой.

2. Все сплавы прямой, проходящей через одну из вершин концентраццоного треугольника, содержат в постоянном отношении те ком­поненты, которые располагаются по обе стороны от этой прямой.

3. Все сплавы, лежащие на высоте концентрационного треугольника, характеризуются одинаковым содержанием тех компонентов, которые располагаются по обе стороны от этой высоты.

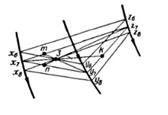
Проследить за изменениями долей различных фаз в сплаве 3 при кристаллизации эвтектики 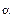+ можно с помощью правила центра тяжести треугольника, которое является дальнейшим развитием пра­вила рычага применительно к трехфазным сплавам. Наряду с треу­гольниками x₆y₆z₆ и x₈y₈z₈ изображающими равновесие фаз в мо­менты начала и конца кристаллизации эвтектики + , на рис. 72 показан еще один треугольник x₇y₇z₇ который изображает эвтекти­ческое равновесие Ж_У7 = _X7 + _Z7 при некоторой промежуточной температуре t_у7 в интервале кристаллизации эвтектики + , когда в сплаве 3 присутствуют все три фазы: Ж_У7, _х7 и _Z7. Если через вершины этого треугольника и фигуративную точку сплава провести три отрезка до пересечения с противоположными сторонами, то с помощью отношений отрезков 3m/my₇, 3k/kx₇ и 3n/nz₇ можно опре­делить доли жидкости Ж_{y7, х7}— _Z7-кристаллов в этом сплаве.

18) Условия, которым должны удовлетворять исходные компоненты для того, чтобы в трой­ной системе могла реализоваться неограничен­ная растворимость: однотипность химических связей, изоморфность кристаллических реше­ток, близость размеров атомных радиусов, небольшое различие в электроотрицательно­сти компонентов.

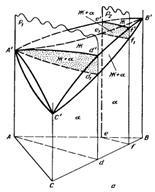
На рис. 11.3, а схематически показана тройная диаграмма с неограниченной раство­римостью. Каждая такая диаграмма слагается из трех двойных диаграмм с неограниченной растворимостью компонентов. А’l'»В’l’С’l»А’ — поверхность ликвидуса, которая представ­ляет собой геометрическое место фигуратив­ных точек жидких растворов предельной кон­центрации; А’S'»В’S’С’S»А’ — поверхность солидуса — геометрическое место фигуратив­ных точек твердых растворов предельной кон­центрации.

В качестве примера рассмотрим кристал­лизацию сплава I (см. рис. 11.3), которая начи­нается при температуре Т_н в точке S_Н и за­канчивается при температуре Т_к в точке S_К на поверхности солидуса. Состав жидкой фа­зы меняется в ходе кристаллизации по кри­вой L_н—Lпр—L_к на поверхности ликвидуса, а состав твердого раствора — по кривой S_Н—S_Пр—S_К на поверхности солидуса. Точки L_пр и S_пр соответствуют составам жидкого и твер­дого растворов при некоторой промежуточной температуре.

Следует заметить, что кривые L_н—L_пр—Ь_к и S_Н—S_пр—S_К (каждая в отдельности и тем более вместе) не лежат в одной вертикальной плоскости. Это видно и по их проекциям L’_я— L’_пр— L’_к и S`<sub>Н</sub>—S`_пр—S`_К на плоскость кон­центрационного треугольника на рис. 11.3.

Конода, соединяющая фигуративные точ­ки жидкой и твердой фаз, находящихся в рав­новесии при каждой данной температуре, со­храняя в ходе кристаллизации горизонтальное положение, вращается с понижением темпе­ратуры от Т_н до Т_к вокруг вертикальной оси I—I`; при этом одним концом она скользит по поверхности ликвидуса по кривой L_я—Ь_пр—Ь_к, а другим — по поверхности солидуса по кри­вой S_Н—5_пр—5_К.

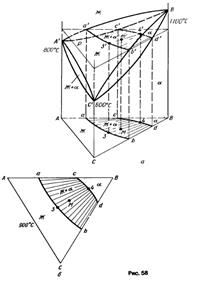
Изотермические разрезы.На рис. 58показаны тройная диаграмма с неограничен­ной растворимостью.

Таким образом, изотермические разрезы характеризуют фазовые равновесия при тем­пературе разреза.

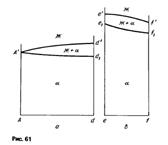
Политермические разрезы.На рис. 60 представлены следы сечения тройной диаграм­мы двумя вертикальными плоскостями, а на рис. 61

19) Тройная диаграмма фазовых равновесий системы с моновариантным (трехфазным) эвтектическим превращением

Тройная диаграмма, в которой реализу­ется моновариантное трехфазное эвтектичес­кое превращение, образована двойными диа­граммами: одна с неограниченной раствори­мостью компонентов друг в друге в твердом и жидком состояниях и две с эвтектическим раз­рывом растворимости.

На рисунках 68 и 69 приведена сама диаграммы и и проекция на плоскость соответственно.

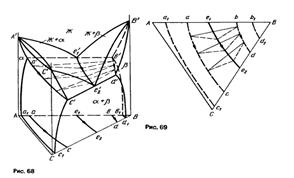Фазовые превращения приведены на рисунках 70 и 71

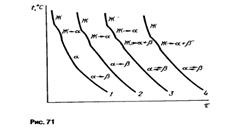Изотермическое сечение.На изотермичес­ком сечении (см. рис. 73)

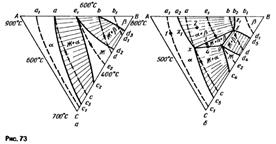Политермическое сечение.Рассмотрим характерный политермический разрез трой­ной диаграммы. Смотри рис. 74.

Источник

Правило фаз Гиббса. Понятие о диаграммах состояния. Типы фазовых диаграмм.

Металлургические процессы осуществляются в сложных гетерогенных системах, включающих различные фазы. Краткое определение понятия фазы:

Более развернутое определение выглядит следующим образом:

Фазой называют гомогенную часть гетерогенной системы или совокупность нескольких частей, разобщенных поверхностями раздела, одинаковых по химическому составу, строению и свойствам, которые не зависят от массы фазы.

Т.е. наличие поверхности раздела между частями системы не всегда указывает на существование разных фаз. Например, совокупность всех кристаллов определенного состава и одинакового кристаллического строения является одной фазой, несмотря на наличие между кристаллами поверхности раздела. Компонентами называются вещества, образующие сплавы.

Гиббсомбыло сформулировано так называемое правило фаз, позволяющее рассчитать максимальное количество фаз в системе, находящейся в равновесии при заданных внешних условиях (давление и температура):

Число степеней свободы (С) в равновесной системе равно разности между числом компонентов (К) и числом фаз +2.

В литературе Вы можете встретить другие определения понятия “число компонентов”, которые, по сути, отражают то же самое, что приведенное выше определение. Например:

Компонентами фазы называют индивидуальные вещества, способные существовать в изолированном виде, наименьшее число которых достаточно для образования всех фаз системы». Таким образом, компонентами называют не общее число составляющих систему веществ, а такое их число, которое достаточно для выражения состава любой фазы системы.

Из правила фаз следует, что число фаз в любой гетерогенной системе не может больше, чем К+2, т.к. число степеней свободы не может быть отрицательным. В многокомпонентных системах независимыми параметрами, определяющими состояние системы являются: общее давление, температура и концентрации компонентов (N_Me, N_x) или их соотношение.

В 2-х компонентной системе Me-X максимальное число фаз при С=0 равно 4 (газ + 3 конденсированные фазы). В 3-х компонентной системе Ф_макс.=5 и т.д.

Графически фазовые равновесия изображаются с помощью фазовых диаграмм или диаграмм состояния.

На практике нередко встречаются диаграммы, на которых отражаются и неравновесные состояния, например, переохлажденные или перегретые жидкие и твердые фазы. Поэтому, полностью с понятием «диаграмма состояния» не следует отождествлять понятие «диаграмма равновесия фаз», которое отражает равновесное состояние системы, т.е. состояние, когда в системе все превращения полностью завершились. Строго говоря, диаграммами равновесия фаз являются теоретически выведенные диаграммы состояния, т.к. в экспериментальных исследованиях, как правило, не достигается состояния равновесия, и изучаются превращения с различным приближением к этому состоянию. Однако, в большинстве случаев, диаграммы состояния достаточно близко отражают именно равновесное фазовое состояние систем.

Диаграммы состояния несут в себе много полезной информации металлургам, имеющим дело с высокотемпературными (пиро-) процессами. Во многих случаях не прибегая к сложным термодинамическим расчетам, они позволяют ответить на весьма важные вопросы о возможности осуществления того или иного процесса, составах образующихся фаз, условиях существования жидких фаз и т.д. Поэтому для металлургов фазовые диаграммы весьма важны полезны.

Более всего распространены и хорошо изучены двойные диаграммы основополагающих систем, таких как Fe-C, Fe-O, Fe-S, Cu-S и др. Менее изучены тройные, четверные и т.д. системы как существенно более сложные.

Прежде чем перейти к рассмотрению типичных проекций диаграмм состояния в координатах Ме-Х,хотелось бы высказать некоторые соображения о строении твердых химических соединений в этой системе. Состав соединений, например оксидов или сульфидов, не отвечает химической формуле, которая ему приписывается, т.е. закон простых кратных отношений не является вполне строгим. Вблизи соединения обязательно существует большая или меньшая область гомогенности. Для доказательства этого положения допустим, что такой области нет и что состав соединения АВфазовой диаграммы, изображенной на рисунке 3.1 точно отвечает стехиометрии. Тогда при температуре t₁ в области Iв равновесии находятся жидкость состава а, кристаллы b и газовая фаза. Из правила фаз следует, что для области Iчисло степеней свободы равно 1. Задавая температуру t, мы используем эту единственную степень свободы. Это значит, что для любых сплавов, лежащих на прямой аb состава фаз, химические потенциалы компонентов и равновесные давления кислорода (серы) остаются постоянными и жидкость состава а находится в равновесии с кристаллами b.Аналогично для области II кристаллы состава b должны находиться в равновесии с жидкостью состава c. Таким образом, если допускаем отсутствие области гомогенности вблизи соединения АВ, то приходим к абсурдному выводу о том, что кристаллы состава b одновременно находятся в равновесии с жидкостью состава а и жидкостью состава с. Поскольку газовая фаза в системе общая, это означает, что равновесное давление кислорода (серы) над жидкостями составов а и с равны., чего быть не может, поскольку составы жидкостей и поэтому активности компонентов А и В в них существенно различны. На основании изложенного неизбежно приходим к выводу, что в соответствии с фундаментальными законами физической химии вблизи соединения АВ обязана существовать область гомогенности, внутри которой равновесное давление летучего компонента меняется от значений, отвечающих жидкости состава а, до значений, отвечающих жидкости состава с. То же относится и к другим термодинамическим функциям. Отметим попутно, что в системе А-В не могут существовать также чистые компоненты А и В и что вблизи чистых компонентов также обязательно должна существовать большая иди меньшая область взаимной растворимости компонентов.

Рисунок 3.1. Гипотетическая диаграмма состояния системы с одним химическим соединением

В соответствии с правилом фаз, каждой точке области гомогенности отвечает строго определенное равновесное давление летучего компонента. Это равновесное давление получило название упругость диссоциации. Если давление летучего компонента над системой не соответствует равновесному давлению, то в системе будут протекать процессы, приводящие к изменению состава фазы. По этой причине исключительно важно знать равновесные давления для всех областей фазовых диаграмм.

Рассмотрим сначала системы, в которых один компонент нелетучий металл, другой летучий элемент или газ (O₂,, S₂, Р₂, Сl₂ и т.д.).

Начнем разбирать с системы, в которой образуется одно химическое соединение (рисунок 3.2). В системе А—В имеются пять гомогенных областей (Х, IХ, III, У, УIII), имеющих две степени свободы, ишесть двухфазных областей (1, II, IУ, УI, УII, ХI) с одной степенью. Согласно правилу фаз, в моновариантных областях над всеми сплавами при постоянной температуре (например, на изотерме D-X) создается постоянное давление. Составы фаз также постоянны, поскольку единственная степень свободы была использована была задана температура. Таким образом, изотерма Т-X на Р-Т- проекции проектируется в точку, а вся двухфазная область, или совокупность этих точек, соответствующих изотермам для всего диапазона температур. Далее по диаграммам рассматриваются вопросы:

* области гомогенности, понятие, расположение на диаграмме, число степеней свободы в областях гомогенности двухфазных систем;

* двухфазные (конденсированные) области (моновариантного равновесия), расположение на диаграмме, число степеней свободы в двухфазных (гетерогенных) областях двухфазных систем;

* линии ликвидуса, солидуса;

* твердые химические соединения на диаграммах состояния, области гомогенности хим. соединений

Аналогично рассматриваются другие типы диаграмм бинарных систем, приведенных на рисунках 3.3-3.5.

Рисунок 3.4. Диаграмма состояния системы с одним устойчивым химическим соединением и областью расслаивания.

Рисунок 3.5 Диаграмма состояния системы с одним устойчивым химическим соединением и областью расслаивания.

Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам.

ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала.

Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все.

Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Источник