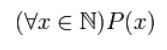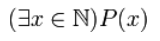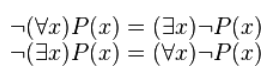Что такое область истинности предиката

Предикаты и области истинности

Минобрнауки России

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ

институт информационных наук и технологий безопасности

ФАКУЛЬТЕТ ЗАЩИТЫ ИНФОРМАЦИИ

ПРЕДИКАТЫ И ОПЕРАЦИИ НАД НИМИ. мНОЖЕСТВА ИСТИННОСТИ ПРЕДИКАТОВ. КВАНТОРЫ

студентов 2 курса направления подготовки

090900 «Информационная безопасность» (бакалавриат)

Предикаты и операции над ними.

Предика́т (n-местный, или n-арный) — это функция с множеством значений (или «ложь» и «истина»), определённая на множестве . Таким образом, каждый набор элементов множества M характеризуется либо как «истинный», либо как «ложный».

Предикат можно связать с математическим отношением: если (m₁,m₂. m_n) принадлежит отношению, то предикат будет возвращать на ней 1. В частности, одноместный предикат определяет отношение принадлежности некоторому множеству.

Предикат — один из элементов логики первого и высших порядков. Начиная с логики второго порядка, в формулах можно ставить кванторы по предикатам.

Предикат называют тождественно-истинным и пишут:

если на любом наборе аргументов он принимает значение 1.

Предикат называют тождественно-ложным и пишут:

если на любом наборе аргументов он принимает значение 0.

Предикат называют выполнимым, если хотя бы на одном наборе аргументов он принимает значение 1.

Так как предикаты принимают только два значения, то к ним применимы все операции булевой алгебры – конъюнкция, дизъюнкция, импликация и отрицание.

Примеры

Например, обозначим предикатом EQ(x, y) отношение равенства («x = y»), где x и y принадлежат множеству вещественных чисел. В этом случае предикат EQ будет принимать истинное значение для всех равных x и y.

Более житейским примером может служить предикат ПРОЖИВАЕТ(x, y, z) для отношения «x проживает в городе y на улице z» или ЛЮБИТ(x, y) для «x любит y», где множество M — это множество всех людей.

Операции над предикатами

Предикаты, так же, как высказывания, принимают два значения истинное и ложное, поэтому к ним применимы все операции логики высказываний. Рассмотрим применение операций логики высказываний к предикатам на примерах одноместных предикатов.

Логические операции

Конъюнкцией двух предикатов А(х) и В(х) называется новый предикат A(x)&B(x), который принимает значение «истина» при тех и только тех значениях Т, при которых каждый из предикатов принимает значение «истина», и принимает значение «ложь» во всех остальных случаях. Множеством истинности Т предиката А(х)&В(х), является пересечение множеств истинности предикатов А(х) – Т₁ и В(х) – Т₂, т.е. Т = Т₁∩Т₂.

Пример: А(х): «х – четное число», В(х): « х кратно 3». А(х) В(х) – «х – четное число и х кратно 3». Т.е. предикат «х делится на 6».

Дизъюнкцией двух предикатов А(х) и В(х) называется новый предикат , который принимает значение «ложь» при тех и только тех значениях Т, при которых каждый из предикатов принимает значение «ложь» и принимает значение «истина» во всех остальных случаях. Областью истинности предиката является объединение областей истинности предикатов А(х) и В(х).

Импликацией предикатов А(х) и В(х) называется новый предикат 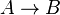, который является ложным при тех и только тех значениях Т, при которых А(х) принимает значение «истина», а В(х) – значение «ложь» и принимает значение «истина» во всех остальных случаях. Читают: «Если А(х), то В(х)».

Пример. А(х): «Натуральное число х делится на 3». В(х): «Натуральное число х делится на 4», можно составить предикат: «Если натуральное число х делится на 3, то оно делится и на 4». Множеством истинности предиката 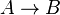является объединение множества Т2 – истинности предиката В(х) и дополнения к множеству Т1 истинности предиката А(х).

Предикаты и области истинности

Кроме высказываний, рассматриваются также высказывания с переменными, т.е. буквами, вместо которых можно подставлять определенные значения (например, числа). Если вместо всех переменных подставить их значения, то высказывание с переменными превратится в обычное высказывание.

Например, рассмотрим высказывание с переменной

.

—истинное высказывание,

— ложное высказывание.

Те наборы значений переменных, при которых получается истинное высказывание, образуют область истинности высказывания с переменными.

Определение. Предикат — это высказывание с переменными.

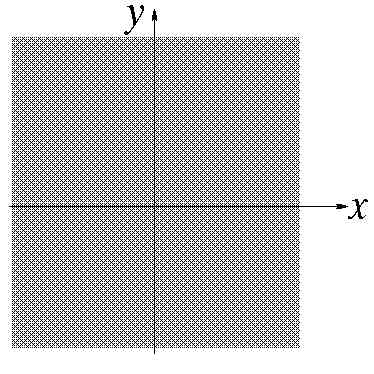
Пример. Область истинности предиката

— ;
предиката — ;
предиката :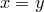

Область истинности предиката , где
— свободные переменные, — связанная переменная:

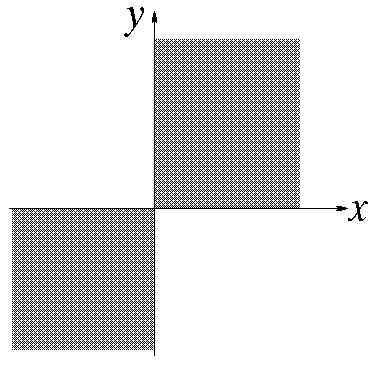
Область истинности предиката 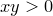(оси координат не включаем):

Область истинности предиката :

Если в предикаты P и Q входят одни и те же переменные, то область истинности предиката есть пересечение, а область истинности предиката — объединение областей истинности данных предикатов.

Кванторы

Ква́нтор — общее название для логических операций, ограничивающих область истинности какого-либо предиката и создающих выcказывание. Чаще всего упоминают:

· Квантор всеобщности (обозначение: , читается: «для всех…», «для каждого…» или «каждый…», «любой…», «для любого…»).

· Квантор существования (обозначение: , читается: «существует…» или «найдётся…»).

В математической логике приписывание квантора к формуле называется связыванием или квантификацией.

В многозначных логиках также вводятся и другие кванторы, например, квантор плюральности (квантор Решера) (обозначается перевёрнутой M, читается «для большинства …»).

Примеры

Обозначим предикат «x делится на 5». Используя квантор общности, можно формально записать следующие высказывания (конечно, ложные):

1. любое натуральное число кратно 5;

2. каждое натуральное число кратно 5;

3. все натуральные числа кратны 5;

.

Следующие (уже истинные) высказывания используют квантор существования:

1. существуют натуральные числа, кратные 5;

2. найдётся натуральное число, кратное 5;

3. хотя бы одно натуральное число кратно 5.

Их формальная запись:

.

Высказывание означает, что область значений переменной включена в область истинности предиката .

(«При всех значениях (x) утверждение верно»).

Высказывание означает, что область истинности предиката непуста.

(«Существует (x), при котором утверждение верно»).

Дата добавления: 2018-02-15 ; просмотров: 5258 ; Мы поможем в написании вашей работы!

Источник

Предикаты и кванторы

Вы будете перенаправлены на Автор24

Понятие предиката

Предикатом в программировании является функция, которая принимает один или более аргументов и возвращает значения булева типа.

Предикат называется тождественно-истинным, если на любом наборе аргументов он принимает истинное значение:

Предикат называется тождественно-ложным, если на любом наборе аргументов он принимает ложное значение:

Предикат называется выполнимым, если хотя бы на одном наборе аргументов он принимает истинное значение.

Примеры предикатов

Таким образом, предикатом является все то, что утверждается или отрицается о субъекте суждения.

Готовые работы на аналогичную тему

Операции над предикатами

Рассмотрим применение операций алгебры логики к предикатам.

Логические операции:

Над предикатами помимо логических операций можно выполнять квантовые операции: применение квантора всеобщности, квантора существования и т.д.

Кванторы

Чаще всего используют кванторы:

В математической логике существует понятие связывание или квантификация, которые обозначают приписывание квантора к формуле.

Примеры применения кванторов

С помощью квантора всеобщности можно записать следующие ложные высказывания:

который будет иметь вид:

Для записи истинных высказываний используем квантор существования:

Запись будет иметь вид:

Таким образом, предикат можно превратить в высказывание, если поставить перед предикатом квантор.

Операции над кванторами

Для построения отрицания высказываний, которые содержат кванторы, применяется правило отрицания кванторов:

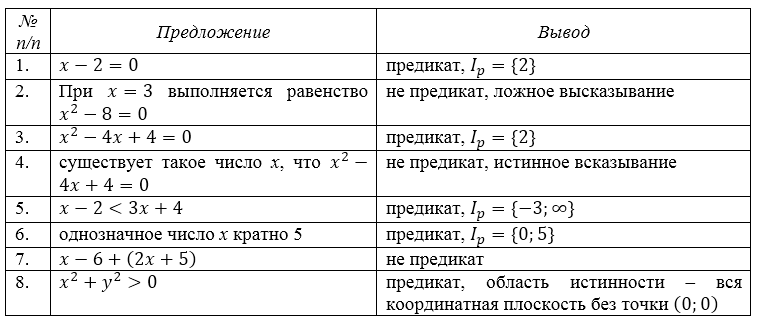
Рассмотрим предложения и выделим среди них предикаты, указав область истинности каждого из них:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата написания статьи: 07 04 2016

Источник

Презентация «Алгебра предикатов» по дисциплине «Элементы математической логики»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

АЛГЕБРА ПРЕДИКАТОВ Преподаватель ГБПОУ КК «АМТ»: Беляева Т.Ю.

1. ПОНЯТИЕ ПРЕДИКАТА Если в предикате одну переменную заменить ее конкретным значением, то местность предиката уменьшается на 1. Т.к. одноместный предикат после подстановки вместо переменной конкретного значения превращается в высказывание, то высказывание – нульместный предикат

2. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ИСТИННОСТИ ПРЕДИКАТА Примеры: 1) Р(х) – «х –четное число» UP = N IP= 2) Q(x) – «2х – 3 = 0» UQ = R, IQ = <1,5>3) P(x, y) – «х кратно у» UP = N2 IP =

2. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ИСТИННОСТИ ПРЕДИКАТА

2. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ИСТИННОСТИ ПРЕДИКАТА Напр.: 1) «(х – у)(х + у) = х2 – у2» – тождественно истинный двуместный предикат 2) «х2 – 2х = 0» – выполнимый одноместный предикат 3) «х + 1 = х» – тождественно ложный одноместный предикат

2. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ИСТИННОСТИ ПРЕДИКАТА Опр. Два предиката называются эквивалентными (равносильными), если они определены на одном и том же множестве и их множества истинности совпадают.

ПРИМЕР Идентифицируйте следующие предложения. Для предикатов найдите их область определения и область истинности. Укажите вид предиката. «х2 + 1» «y 0» «х – 5 = 4х + 1» «n – кратно 5» «х2 – 2х + 3 ≥ 0» «с2 = а2 + в2 »

II. КОНЪЮНКЦИЯ ПРЕДИКАТОВ Опр. Конъюнкцией 2-х предикатов P(x) и Q(x) называется предикат P(x) /\ Q(x), который становится истинным высказыванием лишь при тех значениях х, при которых оба предиката становятся истинными высказываниями. (!!) Очевидно, что множество истинности предиката P(x) /\ Q(x) – есть пересечение множеств истинности исходных предикатов.

III. ДИЗЪЮНКЦИЯ ПРЕДИКАТОВ Опр. Дизъюнкцией 2-х предикатов P(x) и Q(x) называется предикат P(x) \/ Q(x), который становится истинным высказыванием при тех значениях х, при которых хотя бы один из предикатов становится истинными высказываниями. (!!) Очевидно, что множество истинности предиката P(x) \/ Q(x) – есть объединение множеств истинности исходных предикатов.

V. ЭКВИВАЛЕНЦИЯ ПРЕДИКАТОВ Опр. Эквиваленцией 2-х предикатов P(x) и Q(x) называется предикат P(x) ↔ Q(x), который становится истинным высказыванием при тех значениях х, при которых предикаты Р(х) и Q(x) становятся высказыванием с одинаковыми значениями истинности.

ПРИМЕР На множестве А = <3; 4; 5; …; 17>заданы предикаты: Р(х) – «х кратно 3», Q(x) – «х – составное число», S(x) – «х – нечетное число». Найдите множества истинности следующих предикатов: 1) Q (x) 2) P(x) /\ Q(x) 3) P(x) \/ S(x); 4) S(x) → Q(x); 5) P(x) ↔ Q(x).

I. КВАНТОР ВСЕОБЩНОСТИ Обозначается: x P(x) Читается: для всех, для любого, для каждого x выполняется условие P(x) все х из U обладают свойством Р(х) Например: 1) P(x) – «Река x имеет исток» x P(x) – «Любая река имеет исток» 2) Р(х) – «х – простое число» x P(x) – «Все натуральные числа простые»

I. КВАНТОР ВСЕОБЩНОСТИ Опр. Переход от одноместного предиката Р(х) к высказыванию xP(x) называется операцией связывания предметной переменной х квантором общности. При этом переменная х называется связанной. (!!) Очевидно, что такое высказывание является истинным тогда и только тогда, когда Р(х) – тождественно истинный предикат.

I. КВАНТОР ВСЕОБЩНОСТИ Рассмотрим теперь двуместный предикат Р(х; у) – «х делится на у», определенный на множестве 2 Ясно, что х Р(х; у) – одноместный предикат от предметной переменной у: «Все натуральные числа делятся на у» При у = 3 – ложное высказывание При у = 1 – истинное высказывание Т.о., это одноместный выполнимый предикат Очевидно, что предикат у Р(х; у) является тождественно ложным предикатом, а х у Р(х; у) – есть ложное высказывание.

II. КВАНТОР СУЩЕСТВОВАНИЯ Обозначается: x P(x) Читается: существует, найдется некоторое, какое-то x, для которого выполняется P(x) Например: 1) P(x) – «Дверь x закрыта» x P(x) – «Существует дверь, которая закрыта» 2) Р(х) – «х – простое число» x P(x) – «Существует простое натуральное число»

II. КВАНТОР СУЩЕСТВОВАНИЯ Опр. Переход от одноместного предиката Р(х) к высказыванию xР(х) называется операцией связывания предметной переменной х квантором существования. (!!) Высказывание xР(х) является ложным тогда и только тогда, когда Р(х) – тождественно ложный предикат.

II. КВАНТОР СУЩЕСТВОВАНИЯ (!!) В п-местном предикате Р(х1; х2; …; хп) некоторые предметные переменные могут быть связаны квантором общности, а некоторые – квантором существования. Местность такого предиката определяется числом свободных переменных. Напр.: х у P(x; y; z) – одноместный предикат от переменной z.

3. ПРЕДИКАТНАЯ ФОРМУЛА 4) Если Ф1 и Ф2 – формулы, имеющие одинаковый характер вхождения предметных переменных, то Ф1  Ф2, Ф1  Ф2, Ф1 → Ф2, Ф1 ↔ Ф2 – формулы алгебры предикатов. В этих формулах те переменные, которые в исходных формулах были свободны, являются свободными, а те, которые были связанными, остаются связанными.

5. ПРЕДИКАТНАЯ ФОРМУЛА (!!)1 Очевидно, что все формулы алгебры высказываний являются формулами алгебры предикатов. (!!)2 Иерархия логических операций остается та же, что и в алгебре высказываний, однако, следует иметь в виду, что кванторы связывают сильнее, чем другие логические связки.

5. ПРЕДИКАТНАЯ ФОРМУЛА Опр. Две формулы алгебры предикатов называются равносильными на области U, если они принимают одни и те же истинностные значения, какие бы значения ни придавались входящим в них переменным из области U. (!!) Все равносильности, известные в алгебре высказываний, распространяются на алгебру предикатов. Кроме них в алгебре предикатов существуют равносильности c кванторами.

6. РАВНОСИЛЬНОСТИ С КВАНТОРАМИ 1. Если предикат определен на конечном множестве М = <а1,…, ап>, то а) x P(x) ≡ Р(а1)  Р(а2)  …  Р(ап) б) x P(x) ≡ Р(а1)  Р(а2)  …  Р(ап) Т.о., кванторы – другая форма записи конъюнкции и дизъюнкции. (!!) Кванторная форма записи конъюнкции и дизъюнкции пригодна и в случае, когда область определения предиката – бесконечное множество.

6. РАВНОСИЛЬНОСТИ С КВАНТОРАМИ 2. Знак отрицания можно внести под знак квантора, изменив квантор на двойственный, т.е.: а) x P(x) ≡ x P(x); б) х P(x) ≡ x P(x). (!!) Это правило справедливо для многокванторных предикатов.

6. РАВНОСИЛЬНОСТИ С КВАНТОРАМИ 3. Квантор общности обладает распределительным свойством относительно конъюнкции, т.е.: x (P(x)  Q(x)) ≡ x P(x)  x Q(x); 4. Квантор существования обладает распределительным свойством относительно дизъюнкции, т.е.: х (P(x)  Q(x)) ≡ x P(x)  x Q(x).

6. РАВНОСИЛЬНОСТИ С КВАНТОРАМИ 5. Одноимённые кванторы можно менять местами, т.е.: x у P(x; у) ≡ у x P(x; у); x у P(x; у) ≡ у x P(x; у). (!!) Разноименные кванторы менять местами нельзя.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-983290

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

В Петербурге школьникам разрешили уйти на каникулы с 25 декабря

Время чтения: 2 минуты

Более 50 российских школ перешли на дистанционку из-за коронавируса

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

В МГПУ сформулировали новые принципы повышения квалификации

Время чтения: 4 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник