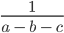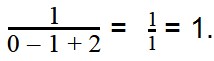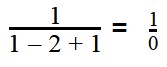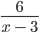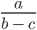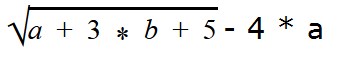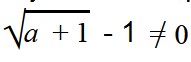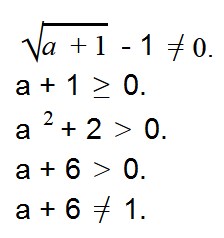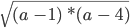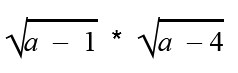Что такое область определения уравнения
Область определения функции
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие области определения функции
Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.
Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.
Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).
Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.
Из понятия функции сформулируем определение области определения функции.
Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
Чтобы обозначить область определения некоторой функции f, используют запись D(f). При этом нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.
Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].
Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:
Например, все действительные числа от 2 до 5 включительно можно записать так:
Все положительные числа можно описать так:
Ноль не положительное число, поэтому скобка возле него круглая.
Области определения основных элементарных функций
Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.
На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.
Рассмотрим области определения основных элементарных функций.
Область определения постоянной функции
Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.
Смысл функции — в том, что каждому значению аргумента соответствует значение, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.
Константная функция — функция, которая для любого элемента из области определения возвращает одно и то же заданное значение. Множество значений такой функции состоит из одного единственного элемента.
Область определения функции с корнем
Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.
Рассмотрим две вариации такой функции.
Область определения корня зависит от четности или нечетности показателя:
Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).
Пример
Найти область определения функции:
Так как подкоренное выражение должно быть положительным, то решим неравенство x 2 + 4x + 3 > 0.
Разложим квадратный трёхчлен на множители:
Дискриминант положительный. Ищем корни:
Значит парабола a(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 2 + 4x + 3 > 0).
Область определения степенной функции
Область определения степенной функции зависит от значения показателя степени.
Перечислим возможные случаи:
Рассмотрим несколько примеров.
Область определения показательной функции
Область определения показательной функции — это множество R.
Примеры показательных функций:
Область определения каждой из них (−∞, +∞).
Область определения логарифмической функции
Логарифмическая функция выглядит так: y = logax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.
Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:
Рассмотрим примеры логарифмических функций:
Область определения этих функций есть множество (0, +∞).
Пример
Укажите, какова область определения функции:
Составим и решим систему:
Область определения тригонометрических функций
Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.
Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что 
Пример
Найдите область определения функции f(x) = tg2x.
Так как a(x) = 2x, то в область определения не войдут следующие точки:
Перенесем 2 из левой части в знаменатель правой части:
В результате 
Ответ: область определения: 
Область определения обратных тригонометрических функций
Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.
Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.
Таблица областей определения функций
Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.
И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.
Функция
Область определения функции
Как найти область определения функции?
Что значит найти область определения
После того, как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y = f ( x ) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Ограничение области определения
Правила нахождения области определения
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно, чтобы имело место следующее утверждение:
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом для понимания перечисления числовых множеств.
Найти область определения функции вида y = x 7 + x + 5 + t g x .
Для нахождения области определения произведения функций необходимо применять правило:
Ответ: область определения y = 3 · a r c t g x · ln x – множество всех действительных чисел.
Необходимо рассмотреть как разность двух функций f 1 и f 2 .
Для нахождения области определения функции y = log 3 x − 3 · 2 x получим, что
Область определения сложной функции
Видно, что область определения сложной функции вида y = f 1 ( f 2 ( x ) ) находится на пересечении двух множеств таких, где x ∈ D ( f 2 ) и f 2 ( x ) ∈ D ( f 1 ) . В стандартном обозначении это примет вид
x ∈ D ( f 2 ) f 2 ( x ) ∈ D ( f 1 )
Рассмотрим решение нескольких примеров.
Тогда получим систему неравенств вида
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.
Преобразуем систему вида
Заданная функция может быть расписана, как y = f 1 ( f 2 ( f 3 ( x ) ) ) , где имеем f 1 – функция синуса, f 2 – функция с корнем 4 степени, f 3 – логарифмическая функция.
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0
Область определения логарифма с переменной в основании
x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 f 2 ( x ) ≠ 1
А аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 log a f 2 ( x ) ≠ 0 = x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 f 2 ( x ) ≠ 1
Область определения показательно-степенной функции
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.Ф
Сумма, разность, произведение функций
Расположим функции и их области определения.
Прямая пропорциональность y = k · x
Обратная пропорциональность y = k x
Дробная y = f 1 ( x ) f 2 ( x )
y = log f 2 ( x ) f 1 ( x )
В частности, y = log a f 1 ( x )
В частности, y = log f 2 ( x ) a
Область допустимых значений функции
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Допустимые и недопустимые значения переменных
В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.
Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.
Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.
Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.
Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.
Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.
Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.
Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.
Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.
Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.
Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.
В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.
Пример 1
Рассмотрим выражение
В выражении три переменные (a, b, c).
Запишем значения переменных в виде: a = 1, b = 1, c = 2.
Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:
Таким же образом можем выяснить, какие значения переменных — недопустимые.
Подставим значения переменных в выражение
На ноль делить нельзя.
Что такое ОДЗ
ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».
Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.
Пример 2
Рассмотрим выражение
Пример 3
Рассмотрим выражение
ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.
Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Как найти ОДЗ: примеры решения
Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.
Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.
Мы не можем вычислить значение выражения, если:
Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.
Давайте потренируемся находить ОДЗ.
Пример 4
Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.
В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.
ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.
Ответ: (a и b), где a — любое число и b — любое число.
Пример 5
Найдем область допустимых значений (ОДЗ) переменной выражения
Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.
Это значит, что мы может сказать, что ОДЗ переменной a в выражении 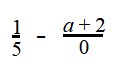
Пустое множество изображается в виде вот такого символа Ø.
Пример 6
Найдем область допустимых значений (ОДЗ) переменных в выражении
Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.
Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.
Пример 7
Найдем ОДЗ переменной a в выражении
Прежде всего, нам нужно подобрать такое условие, при котором в знаменателе дроби не будет ноля —
Мы знаем, что выражение под знаком корня должно быть положительным. Это дает нам второе условие: a + 1 ≥ 0.
Мы не можем вычислить логарифм отрицательного выражения. Получаем третье условие: a 2 + 2 > 0.
Выражении в основании логарифма не должно быть отрицательным и не должно равняться единице. Получаем условие 4: a + 6 > 0.
Как видите, записывая ОДЗ, мы ставим квадратные и круглые скобки.
Запомните
Например, если х > 6, но х
Зачем учитывать ОДЗ при преобразовании выражения
Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.
Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.
Тождественное преобразование может:
Рассмотрим каждый случай в отдельности.
Пример 8
Поскольку мы должны следить за тем, чтобы в выражении не возникало деление ноль, определяем условие a ≠ 0.
Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).
В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.
ОДЗ для a — это R — множество всех вещественных чисел.
Преобразование расширило ОДЗ — добавился ноль.
Пример 9
Рассмотрим выражение a 2 + a + 4 * a
ОДЗ a для этого выражения — множество R.
В выражении есть подобные слагаемые, выполним тождественное преобразование.
После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a
ОДЗ переменной a для этого выражения — множество R.
Это значит, что тождественное преобразование никак не повлияло на ОДЗ.
Пример 10
Рассмотрим выражение
Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).
Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.
Приведем выражение к виду
Решив систему линейных неравенств, получаем множество [4; + ∞).
Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).
Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.
Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.
Определение числовой функции. Область определения функции. Область значения функции.
Что такое область определения функции? что такое область значения функции? Давайте, в этой статье разберемся в понятиях числовой функции и ее характеристиках и свойствах.
Определение функции.
Функция y=f(x) — это когда каждому допустимому значению переменной x соответствует единственное значение переменной y или другими словами такая зависимость переменной y от переменной x.
х — называется независимой переменной или аргументом.
y – называется зависимой переменной или значением функции.
Множество чисел, где x∈X или D(f) — называется областью определения функции. Это множество всех допустимых значений переменной х.
Область значений функций, когда задаем правило или функцию, которая позволяет по произвольно выбранному значению x∈D(f) вычислить соответствующее значение y.
Переменную х или аргумент мы придумываем сами и подставляем в правило, которое задали или функцию. Далее рассчитываем переменную y или значение функции.
В тех диапазонах в которых существует переменная х называется областью определения функции.
В тех диапазонах в которых существует переменная y называется областью значения функции.
Графиком функции y=f(x), x∈X называется множество точек (x; f(x)) координатной плоскости.
Разберём пример №1:
Найдите область определения и область значения числовой функции y=x 2
Вместо переменной x мы можем брать любые числа и просчитать переменную y.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 |
По графику также видно, что сколько бы угодно мы не проводили линий через ось х, мы найдем пересечение с графиком.
А теперь рассмотрим переменную у. В таблице мы видим, что переменная y принимает положительные значение, так как и самое минимальное значение 0. Следовательно, y∈[0; +∞).
Если посмотрим на график, то увидим, что графика ниже нуля нет. Следовательно, область значения функции E(f) = [0; +∞).
Разберём пример №2:
Найдите область определения и область значения числовой функции y=x+1?
Вместо переменной x мы можем брать любые числа и просчитать переменную y.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
По графику также видно, что сколько бы угодно мы не проводили линий через ось х, мы найдем пересечение с графиком.

Рассмотрим переменную у. В таблице мы видим, что переменная y также принимает значения как в положительном, так и в отрицательном направлении. Следовательно, ограничений у переменной y нет, y∈(−∞; +∞). Область значения функции E(f) = (−∞; +∞).