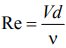Что такое обобщенный параметр рейнольдса
Формула числа Рейнольдса Re
Калькулятор для расчета Re онлайн
Расчет по общей формуле
Расчет Re для воды
Расчет Re для воздуха
Формула
Расчетная формула числа Рейнольдса Re в общем виде:
Для труб круглого сечения расчетная формула числа Рейнольдса Re будет:
Физический смысл
Физический смысл – число Рейнольдса Re характеризует смену режимов течения от ламинарного к турбулентному. Re является критерием подобия течения вязкой жидкости.
Критерий назван в честь выдающегося английского физика Осборна Рейнольдса (1842—1912).
В настоящее время не существует строгого научно доказанного объяснения этому явлению, однако наиболее достоверной гипотезой считается следующая: смена режимов движения жидкости определяется отношением сил инерции к силам вязкости в потоке жидкости. Если преобладают первые, то режим движения турбулентный, если вторые – ламинарный.
Режимы течения
Режим течения в динамическом пограничном слое зависит от числа Рейнольдса Re и может быть:
Критическое значение
Переход к турбулентному режиму течения жидкости в пограничном слое определяется критическим значением числа Рейнольдса. Это обусловлено тем, что при возрастании скорости, участвующей в расчете числа Re, его значение растет.
Таким образом, переход от ламинарного режима к турбулентному наблюдается при определенной скорости движения жидкости. Эта скорость называется критической Vкр.
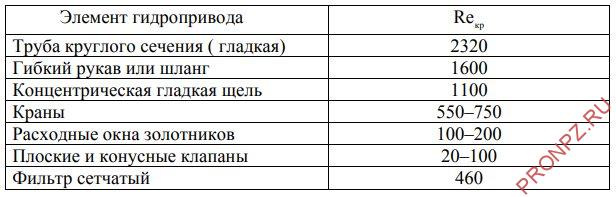
Значение критического числа Re для различных элементов гидропривода
Размерность
Числе Re не имеет единиц измерения. Re является безразмерным критерием подобия течения вязкой жидкости.
Течение в трубе
При ламинарном течении жидкости в прямой трубе или канале постоянного сечения все линии тока направлены параллельно оси трубы, при этом отсутствуют поперечные перемещения частиц жидкости.
При турбулентном течении в канале наряду с основным продольным перемещением жидкости в трубе наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости.
Зависимость режима течения от значения числа Re в гладких трубах:
Обычно предполагается, что при числе Re выше 2300 образуется турбулентный режим.
Тем не менее, при значениях Re выше критического и до определённого предела наблюдается переходной (смешанный) режим течения жидкости, когда турбулентное течение более вероятно, но ламинарное в некоторых конкретных случаях тоже наблюдается — так называемая неустойчивая турбулентность. В трубах такой переходный интервал может достигать вплоть до Re = 2300—10 000.
Рейнольдса число
Число Рейно́льдса — безразмерное соотношение, которое, как принято считать, определяет ламинарный или турбулентный режим течения жидкости или газа. Число Рейнольдса также считается критерием подобия потоков.
Число Рейнольдса определяется следующим соотношением: 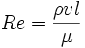
Число Рейнольдса как критерий перехода от ламинарного к турбулентному режиму течения и обратно относительно хорошо действует для напорных потоков. При переходе к безнапорным потокам переходная зона между ламинарным и турбулентным режимами возрастает, и использование числа Рейнольдса как критерия не всегда правомерно. Например, в водохранилищах формально вычисленные значения числа Рейнольдса очень велики, хотя там наблюдается ламинарное течение.
Критерий назван в честь выдающегося английского физика О. Рейнольдса (англ.)(1842—1912), автора многочисленных пионерских работ по гидродинамике.
Физический смысл
Число Рейнольдса есть отношение сил инерции, действующих в потоке, к силам вязкости. Также число Рейнольдса можно рассматривать как отношение кинетической энергии жидкости к потерям энергии на характерной длине.
Безразмерные числа в физике
Полезное
Смотреть что такое «Рейнольдса число» в других словарях:
РЕЙНОЛЬДСА ЧИСЛО — (по имени англ. учёного О. Рейнольдса (О. Reynolds)), один из подобия критериев для течений вязких жидкостей и газов, характеризующий соотношение между инерц. силами и силами вязкости: Re=rvl/m, где r плотность, m коэфф. динамич. вязкости… … Физическая энциклопедия
Рейнольдса число — (по имени О. Рейнольдса) безразмерный параметр, характеризующий собой соотношение инерционных сил и сил внутреннего трения в потоке жидкости или газа. Равен произведению плотности (е), характерных значений скорости V и линейного размера L,… … Энциклопедия техники
Рейнольдса число — безразмерная величина, являющаяся одной из основных характеристик течения вязкой жидкости и равная отношению сил инерции к силам вязкости: Re = ρvl/μ, где ρ плотность жидкости, v характерная скорость (например, скорость потока), l характерный… … Энциклопедический словарь
Рейнольдса число — Reinoldso skaičius statusas T sritis Energetika apibrėžtis Apibrėžtį žr. priede. priedas( ai) MS Word formatas atitikmenys: angl. Reynolds number vok. Reynolds Zahl, f rus. Рейнольдса число, n pranc. nombre de Reynolds, m … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas
Рейнольдса число — (по имени О. Рейнольдса) безразмерный параметр, характеризующий собой соотношение инерционных сил и сил внутреннего трения в потоке жидкости или газа. Равен произведению плотности ρ, характерных значений скорости V и линейного размера L,… … Энциклопедия «Авиация»
Рейнольдса число — (по имени О. Рейнольдса) безразмерный параметр, характеризующий собой соотношение инерционных сил и сил внутреннего трения в потоке жидкости или газа. Равен произведению плотности ρ, характерных значений скорости V и линейного размера L,… … Энциклопедия «Авиация»
Рейнольдса число — один из подобия критериев (См. Подобия критерии) для течений вязких жидкостей и газов, характеризующий соотношение между инерционными силами и силами вязкости: Re = ρvl/μ, где ρ плотность, μ динамический коэффициент вязкости жидкости или… … Большая советская энциклопедия
РЕЙНОЛЬДСА ЧИСЛО — один из критериев подобия для течений вязких жидкостей и газов, характеризующий соотношение между инерционными силами и силами вязкости: где r плотность, m динамич. коэффициент вязкости жидкости или газа, v характерная скорость потока, l… … Математическая энциклопедия
РЕЙНОЛЬДСА ЧИСЛО — безразмерная величина, являющаяся одной из осн. характеристик течения вязкой жидкости и равная отношению сил инерции к силам вязкости: Re = pvl/n, где р плотность жидкости, v характерная скорость (напр., скорость потока), l характерный линейный… … Естествознание. Энциклопедический словарь
Число Рейнольдса
Движение жидкости, несмотря на кажущуюся на первый взгляд, беспорядочность движения имеет определенные закономерности. Рейнольдс в своих опытах нашел определенные общие условия, при которых возможно существование того или иного режима течения и переход от одного режима к другому.
При проведении опытов Рейнольдс в 1883г. подтвердил существование двух режимов течения жидкости. Ему удалось вычислить безразмерное число, описывающее характер потока вязкой жидкости
Содержание статьи
Опыты Рейнольдса
Опыты проводились на специальном лабораторном стенде, который представлял собой заполненный водой бак Б к которому в нижней части присоединена стеклянная трубка Т. На конце трубки установлен кран К для регулирования расхода жидкости. Расход измеряется с помощью секундомера и мерного бочка М. Бак Б постоянно заполняется водой. Над баком Б расположена ёмкость с краской С. По тонкой трубочке Т1 краска попадает в жидкость, движущуюся в трубке Т. Подачу краски регулирует кран Р.
Опыт №1. Немного приоткрываем кран К. При этом в трубке Т начинается движение жидкости. Открываем кран Р и добавляем в жидкость краску. При небольшой скорости движения в трубке Т краска становится прямолинейной и резко выделяющейся в потоке воды цветной струйкой. Эта струйка не перемешивается с остальной жидкостью. Если ввести в жидкость краску несколькими струйками, то они так и будут двигаться не перемешиваясь с остальной водой.
Опыт №2 При намного большем открытии крана струйка краски начинает искривляться и становится волнообразной. Открывая кран ещё больше и увеличивая скорость потока мы увидим, что струйка краски распадается на отдельные вихри и перемешивается с остальной массой воды
Вывод формулы
Рейнольдс установил, что основными факторами, определяющими характер режима являются:




При этом чем больше размеры поперечного сечения и плотность жидкости и чем меньше её вязкость, тем легче при увеличении скорости осуществить турбулентный режим.
Для характеристики режима движения жидкости Рейнольдсом был выведен безразмерный параметр Re, учитывающий влияние перечисленных выше факторов, называемый число Рейнольдса. Таким образом формула
Число Рейнольдса и режимы течения.
Границы существования того или иного режима движения жидкости определяются двумя критическими значениями числа Рейнольдса:
нижнее критическое числом Рейнольдса Reкр. н.
верхнее критическое числом Рейнольдса Reкр. в.
Значение скорости, соответствующее этим значениям Re называют критическими.
При значениях числа Рейнольдса Re Reкр. в. – только турбулентный. При Reкр. н. 2300 – всегда турбулентный режимы.
При этом движении жидкости в неустойчивой зоне исключается из особого рассмотрения, это приводит к некоторому запасу и большей надежности в гидравлических расчетах в случае, если в этой зоне действительно имеет место ламинарный режим.
Без особого труда можно получить значения для Reкр для любой формы сечения, а не только круглой формы. Вспоминая, что при круглом сечении радиус
подставляем в формулу для определения числа Рейнольдса
Принимая для критического числа Рейнольдса независимо от формы живого сечения величину Reкр. = 2300, находим, что для сечения любой формы критериев для сужения о характере режима движения является величина, равная 2300 / 4 = 575.
Таким образом, режим ламинарный если значение числа Рейнольдса
И режим турбулентный, если
Видео по теме.
На практике в большинстве случаев (движение воды в трубах, каналах, реках) приходится иметь дело с турбулентным режимом. Ламинарный режим встречается реже. Он наблюдается, например, при движении в трубах очень вязких жидкостей, что иногда имеет место в нефтепроводах, при движении жидкости в очень узких трубках и порах естественных грунтов.
Число Рейнольдса: для чего оно нужно, как рассчитывается, упражнения
Содержание:
Число Рейнольдса применяется к любому типу потока жидкости, например к потоку в круглых или некруглых каналах, в открытых каналах и потоке вокруг погруженных тел.
Значение числа Рейнольдса зависит от плотности, вязкости, скорости жидкости и размеров пути тока. Поведение жидкости в зависимости от количества энергии, которая рассеивается из-за трения, будет зависеть от того, является ли поток ламинарным, турбулентным или промежуточным. По этой причине необходимо найти способ определения типа потока.
В 1883 году Осборн Рейнольдс обнаружил, что, если значение этого безразмерного числа известно, можно предсказать тип потока, который характеризует любую ситуацию с проводимостью жидкости.
Для чего нужно число Рейнольдса?
Число Рейнольдса используется для определения поведения жидкости, то есть для определения того, является ли течение жидкости ламинарным или турбулентным. Течение является ламинарным, когда силы вязкости, которые противодействуют движению жидкости, являются доминирующими, и жидкость движется с достаточно малой скоростью и по прямолинейному пути.
Жидкость с ламинарным потоком ведет себя так, как будто это бесконечные слои, которые упорядоченно скользят друг по другу без перемешивания. В круглых воздуховодах ламинарный поток имеет параболический профиль скорости с максимальными значениями в центре воздуховода и минимальными значениями в слоях вблизи поверхности воздуховода. Значение числа Рейнольдса в ламинарном потоке равно ра также 4000.
Переход между ламинарным потоком и турбулентным потоком происходит для значений числа Рейнольдса между 2000 Y 4000.
Как рассчитывается?
Уравнение, используемое для расчета числа Рейнольдса в воздуховоде круглого сечения:
ρ = Плотность жидкости (кг / м 3 )
V = Скорость потока (м 3 / с)
D = Характерный линейный размер пути прохождения жидкости, который в случае круглого воздуховода представляет собой диаметр.
η = динамическая вязкость жидкости (Па · с)
Связь между вязкостью и плотностью определяется как кинематическая вязкость. v = η/ρ, и его единица м 2 / с.
Уравнение числа Рейнольдса как функции кинематической вязкости:
В трубопроводах и каналах с некруглым поперечным сечением характерный размер известен как гидравлический диаметр. DЧАС y представляет собой обобщенный размер пути прохождения жидкости.
Обобщенное уравнение для расчета числа Рейнольдса в трубопроводах с некруглым поперечным сечением:
V´ = Средняя скорость потока =Идет
Мокрый периметр пM представляет собой сумму длин стенок трубопровода или канала, контактирующих с жидкостью.
Вы также можете рассчитать число Рейнольдса жидкости, окружающей объект. Например, сфера, погруженная в жидкость, движущуюся со скоростью V. Сфера испытывает силу сопротивления Fр определяется уравнением Стокса.
Число Рейнольдса шара со скоростью V погруженные в жидкость:
ра также 1 при турбулентном потоке.
Решенные упражнения
Ниже приведены три упражнения по применению числа Рейнольдса: Круглый канал, Прямоугольный канал и Сфера, погруженная в жидкость.
Число Рейнольдса в воздуховоде круглого сечения
Рассчитайте число Рейнольдса пропиленгликоля a 20°C в воздуховоде круглого сечения диаметром 0,5 см. Величина скорости потока равна 0,15 м 3 / с. Какой тип потока?
Плотность жидкости составляет ρ = 1,036 г / см 3 = 1036 кг / м 3
Вязкость жидкости составляет η =0,042 Па · с = 0,042 кг / м.с
Скорость потока V = 0,15 м 3 / с
Уравнение числа Рейнольдса используется для круглого воздуховода.
Течение ламинарное, потому что значение числа Рейнольдса мало по отношению к соотношению ра также 3
Сначала определяется средняя скорость потока.
Гидравлический диаметр DЧАС = 4А / ПM
Число Рейнольдса получается из уравнения ра также = ρV´ DЧАС/η
Течение является турбулентным, поскольку число Рейнольдса очень велико (ра также>2000)
Число Рейнольдса для сферы, погруженной в жидкость
Сферическая частица латексного полистирола радиусом р= 2000 нм брошен вертикально в воду с начальной скоростью величинойV0= 10 м / с. Определите число Рейнольдса частицы, погруженной в воду.
Плотность частицρ=1,04 г / см 3 = 1040 кг / м 3
Число Рейнольдса получается из уравнения ра также = ρV R/η
ра также = (1000 кг / м 3 Икс10 м / с Икс 0,000002 м) / 0,001 кг / (м с)
Число Рейнольдса 20. Течение турбулентное.
Приложения
Число Рейнольдса играет важную роль в механике жидкости и теплопередаче, потому что это один из основных параметров, характеризующих жидкость. Некоторые из его приложений упомянуты ниже.
1-Он используется для моделирования движения организмов, которые перемещаются по жидким поверхностям, таких как: бактерии, взвешенные в воде, которые плавают в жидкости и вызывают беспорядочное движение.
2-Он имеет практическое применение в потоках труб и в каналах циркуляции жидкости, в ограниченных потоках, особенно в пористых средах.
3-В суспензиях твердых частиц, погруженных в жидкость и в эмульсиях.
4-Число Рейнольдса применяется при испытаниях в аэродинамической трубе для изучения аэродинамических свойств различных поверхностей, особенно в случае полетов самолетов.
5-Он используется для моделирования движения насекомых в воздухе.
6-Конструкция химических реакторов требует использования числа Рейнольдса для выбора модели потока с учетом потерь напора, потребления энергии и площади передачи тепла.
7-В прогнозировании теплопередачи электронных компонентов (1).
8-В процессе полива садов и огородов необходимо знать поток воды, выходящей из труб. Чтобы получить эту информацию, определяется гидравлическая потеря напора, которая связана с трением, которое существует между водой и стенками трубы. Потеря напора рассчитывается после получения числа Рейнольдса.
Приложения в биологии
В биологии изучение движения живых организмов в воде или в жидкостях со свойствами, подобными воде, требует получения числа Рейнольдса, которое будет зависеть от размера организмов и скорости, с которой они перемещаются. сместить.
Бактерии и одноклеточные организмы имеют очень низкое число Рейнольдса (ра также1), следовательно, течение имеет ламинарный профиль скорости с преобладанием вязких сил.
Организмы, близкие по размеру к муравьям (до 1 см), имеют число Рейнольдса порядка 1, что соответствует переходному режиму, в котором силы инерции, действующие на организм, столь же важны, как и силы вязкости жидкости.
У более крупных организмов, таких как люди, число Рейнольдса очень велико (ра также1).
Число Рейнольдса
Осборн Рейнольдс был, в некотором смысле, последним приверженцем старых добрых традиций классической механики Ньютона. В конце жизни он даже разработал тщательно продуманную механическую модель светоносного эфира (см. Опыт Майкельсона—Морли), согласно которой эфир представлял собой систему мельчайших шарообразных частиц, свободно перекатывающихся друг относительно друга подобно дробинкам в мешке. До конца своих дней он считал, что «прогрессу механики нет конца. и то, что современники полагают ее пределом и тупиком. со временем окажется лишь новым поворотом на пути ее развития».
Чтобы понять всю важность главного открытия его жизни, нужно сначала немного рассказать о так называемых безразмерных величинах. Предположим, нам нужно измерить геометрические размеры комнаты. Допустим, мы взяли рулетку и определили, что длина комнаты равна 5 метрам. Однако, если мы возьмем рулетку, проградуированную в футах, окажется, что длина комнаты равна 15 с небольшим футов. То есть полученные нами при измерении цифры будут зависеть от используемых единиц, в то время как реальная длина комнаты остается постоянной.
Есть, однако, и такие характеристики геометрии комнаты, которые никак не зависят от единиц измерения. В частности, такой величиной является отношение длины комнаты к ее ширине — так называемое характеристическое соотношение. Если комната имеет длину 20 футов и ширину 10 футов, ее характеристическое соотношение равно 2. Измерив длину и ширину комнаты в метрах, мы получим, что размеры комнаты равны 6,096 м × 3,048 м, однако характеристическое соотношение останется прежним: 6,096 м : 3,048 м = 2. В данном случае 2 — безразмерная характеристика комнаты.
Теперь давайте обратимся к потоку жидкости. Различные жидкости при течении в трубах, растекании по поверхности или обтекании препятствий обладают различными свойствами. Густая, клейкая жидкость (например, мед) обладает, как говорят физики, большей вязкостью, нежели легкая и подвижная жидкость (например, бензин). Степень вязкости жидкости определяется так называемым коэффициентом вязкости, который принято обозначать греческой буквой η («эта»). У густых, клейких жидкостей коэффициент вязкости η в десятки и сотни раз выше, чем у легких и текучих.
Рейнольдсу удалось обнаружить безразмерное число, описывающее характер потока вязкой жидкости. Сам ученый получил его экспериментально, проведя изнурительную серию опытов с различными жидкостями, однако вскоре было показано, что его можно вывести и теоретически из законов механики Ньютона и уравнений классической гидродинамики. Это число, которое теперь называют числом Рейнольдса и обозначают Re, характеризует поток и равно:
где ρ — плотность жидкости, v — скорость потока, а L — характерная длина элемента потока (в этой формуле важно помнить, что Re — это одно число, а не произведение R × e).
Отсюда получаем, что размерность числа Рейнольдса равна:
или, после упрощения,
Итак, все единицы измерения в размерности числа Рейнольдса сокращаются, и оно действительно оказывается безразмерной величиной.
Рейнольдсу удалось выяснить, что при значении этого числа 2000–3000 поток становится полностью турбулентным, а при значении Re меньше нескольких сотен — поток полностью ламинарный (то есть не содержит завихрений). Между двумя этими значениями поток носит промежуточный характер.
Можно, конечно, считать число Рейнольдса чисто экспериментальным результатом, однако его можно интерпретировать и с позиции законов Ньютона. Жидкость в потоке обладает импульсом, или, как иногда говорят теоретики, «инерционной силой». По сути, это означает, что движущаяся жидкость стремится продолжить свое движение с прежней скоростью. В вязкой жидкости этому препятствуют силы внутреннего трения между слоями жидкости, стремящиеся затормозить поток. Число Рейнольдса как раз и отражает соотношение между двумя этими силами — инерции и вязкости. Высокие значения числа Рейнольдса описывают ситуацию, когда силы вязкости относительно малы и не способны сгладить турбулентные завихрения потока. Малые значения числа Рейнольдса соответствуют ситуации, когда силы вязкости гасят турбулентность, делая поток ламинарным.
Число Рейнольдса очень полезно с точки зрения моделирования потоков в различных жидкостях и газах, поскольку их поведение зависит не от реальной вязкости, плотности, скорости и линейных размеров элемента потока, а лишь от их соотношения, выражаемого числом Рейнольдса. Благодаря этому можно, например, поместить в аэродинамическую трубу уменьшенную модель самолета и подобрать скорость потока таким образом, чтобы число Рейнольдса соответствовало реальной ситуации полномасштабного самолета в полете. (Сегодня, с развитием мощной компьютерной техники, нужда в аэродинамических трубах отпала, поскольку воздушные потоки можно смоделировать на компьютере. В частности, первым гражданским авиалайнером, полностью спроектированным исключительно с использованием компьютерного моделирования, стал «Боинг-747». В этой связи любопытно отметить, что при проектировании гоночных яхт и высотных зданий до сих пор практикуется их «обкатка» в аэродинамических трубах.)
Ирландский инженер-физик. Родился в Белфасте, в семье потомственного священника англиканской церкви. После недолгого практического обучения инженерному делу в строительной фирме поступил в Кембридж, по окончании которого, несмотря на относительную молодость, сразу же получил должность профессора кафедры гражданского инженерного дела Оуэнс-колледжа (современный Манчестерский университет), которую и занимал на протяжении 37 лет. Рейнольдс занимался научно-техническими разработками в области гидродинамики и гидравлики, стал основоположником теорий смазки и турбулентности, принципиально усовершенствовал конструкцию центробежных насосов. Для изучения устьевых потоков построил уменьшенную модель дельты реки Мерси.