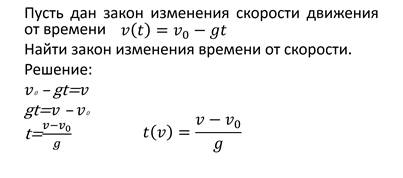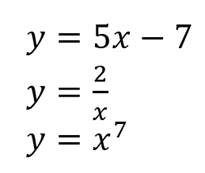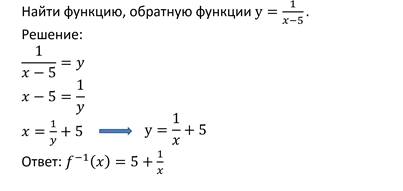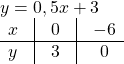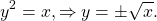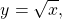Что такое обратимая функция в алгебре 10 класс
Обратная функция
Урок 3. Алгебра 10 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Обратная функция»
· познакомиться с понятиями прямой и обратной функции;
· познакомиться с понятием обратимой функции;
· научиться находить обратные функции;
· рассмотреть свойство обратных функций.
Прежде чем приступить к изучению новой темы, давайте вспомним, что же такое функция и какие основные понятия с ней связаны.
Если даны числовое множество X и правило f, которое позволяет поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y=f(x) с областью определения X.
x – независимая переменная или аргумент.
y – зависимая переменная.
Множество всех значений y=f(x), где x принадлежит множеству X называют областью значений функции и обозначают E(f).
Рассмотрим ещё одну задачу.
Давайте назовём первую задачу прямой, тогда вторая задача будет обратной к первой.
Давайте рассмотрим с вами ещё одну задачу.
Назовём функцию v(t) обратимой функцией, а t(v) – обратной функцией.
Если функция y=f(x) принимает каждое своё значение у только при одном значении x, то эту функцию называют обратимой.
Приведём примеры обратимых функций:
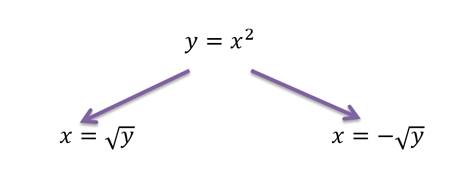
Давайте разберём это определение на примере.
Область определения исходной функции равна области значений обратной функции и наоборот, область значений исходной функции равна области определения обратной функции.
Сформулируем основные свойства обратных функций.
Конспект урока по алгебре и началам анализа 10 класс на тему «Обратная функция»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Урок по теме «Обратная функция»
Цель: Сформировать теоретический аппарат по теме. Ввести понятие обратимой функции; понятие обратной функции; основные свойства взаимно обратных функций.
Актуализация знаний учащихся, необходимая для восприятия новой темы.
Постановка цели перед учащимися.
Изложение нового материала.
Первичное закрепление нового материала.
Постановка домашнего задания.
1. Организационный момент. Приветствие учителя, проверка готовности обучающихся к уроку.
2. Актуализация знаний. (Фронтальный опрос по теме предыдущего урока.)
Что называется функцией?
Какие свойства функций вам известны?
Какие виды функций вам знакомы?
Постановка цели перед учащимися.
Ребята посмотрите в ваши памятки и скажите, все ли виды функции вы изучили? Если нет, поднимите руки (ответ студентов)
Какие виды функций вам пока что не знакомы? (ответ студентов)
Правильно! Кто сможет сформулировать тему нашего урока? (Тема урока: «Обратные функции»)
Каковы цели урока? (ответ студентов: Ввести понятие обратимой функции; понятие обратной функции; основные свойства взаимно обратных функций, научиться строить графики функций обратной и данной) Молодцы!
Изложение нового материала.
Какой вывод сделаем? На графиках под номером 1 и 3 каждому значению функции соответствует единственное значение аргумента. Такая функция называется обратимой
Если функция принимает каждое свое значение только при одном значении x , то эту функцию называют обратимой.
Изобразим график обратимой функции y = f ( x ) у себя в тетрадях.
Покажем, что она обратимая.
Попробуем найти функцию, обратную к данной y =7 x +5.
Давайте составим алгоритм нахождения обратной функции для обратимой.
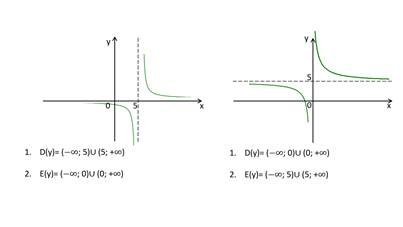
Задача: Найти функцию, обратную к функции y = (пишут в тетрадь)
Прежде чем, выполнять указанное задание, давайте найдем ОО D ( f ) и множество значений функции E ( y ). D ( f ): R кроме x =2, E ( y ): R кроме 0 (пишут в тетрадь)
А сейчас вспоминаем алгоритм.
Т.О. мы получили обратную функцию. Давайте определим для нее ОО и множество значений: D ( f ): R кроме 0, E ( y ): R кроме x =2. (пишут в тетрадь)
Давайте посмотрим на ОО и МЗ данной и обратной функций. Что вы интересного заметили?
Делаем вывод: ОО обратной функции совпадает с множеством значений исходной, а МЗ обратной совпадает с ОО исходной.
Первичное закрепление нового материала. Итак, ребята, мы с вами познакомились с понятиями обратимая и обратная функции, вывели алгоритм нахождения обратной функции, а так же сделали вывод об ОО и МЗ данной и обратной функций.
А сейчас, закрепим полученные знания на практике. Выполним устно № 131.
№ 132, № 133, № 135 (нечетн). (Вызвать к доске)
Задания на карточках
Как называют возрастающие и убывающие функции одним словом? (Монотонные)
Монотонная функция обратима. Т.Е. если данная функция возрастает, то и обратная возрастает. Если исходная функция убывает, то и обратная убывает.
Следующий вопрос, который мы рассмотрим: график обратной функции.
Задача: Построить график функции обратной y = x 2 на промежутке x 0.
Найдем обратную функцию:
Поменять местами x и y:
Построим графики функций в одной системе координат и убедимся, что они симметричны относительно биссектрисы y = x I и III координатных углов
Вывод: если функция имеет обратную, то график обратной функции симметричен графику данной функции относительно прямой y = x
5. Первичное закрепление нового материала. Выполнить №134, № 137
Обратимые и обратные функции
Обратимой называется функция в которой произвольному значению функции соответствует единственное значение аргумента.
Примеры обратимых функций:
Исходная обратимая функция и функция, полученная из нее путем замены x на y и y на x, называются обратными.
Примеры обратных функций:
Однако, если рассматривать данную функцию только на множестве положительных чисел, она будет обратимой:
Графики функций будут симметричны относительно прямой y=x:
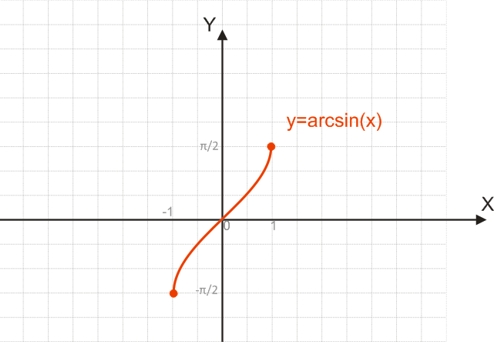
Функция y=arcsin(x)
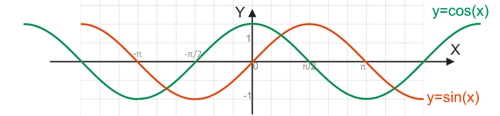
Поскольку функция y=sin(x) является периодической, она не является обратимой.
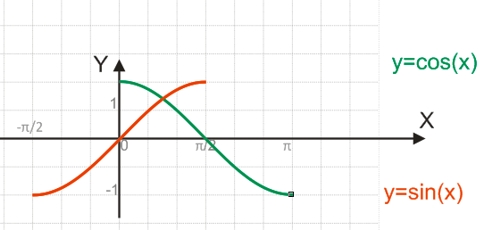
Для построения функции, обратимой y=sin(x), необходимо взять один из полупериодов функции, обычно это отрезок [-π/2;π/2], на котором функция обратима.
График функции y=arcsin(x):
Например, чтобы найти arcsin(1), можно воспользоваться равенством 1=sin(y). Угол на отрезке [-π/2;π/2], синус которого равняется 1, будет равен 90° или π/2.
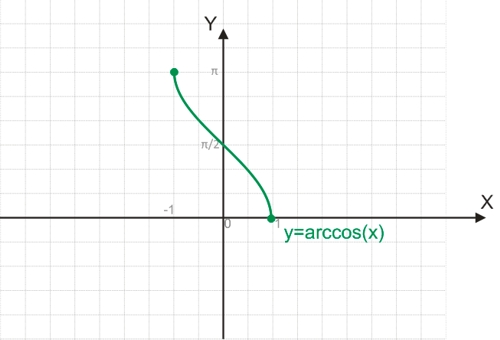
Функция y=arccos(x)
Поскольку функция y=cos(x) является периодической, она не является обратимой.
Для построения функции, обратимой y=cos(x), необходимо взять один из полупериодов функции, обычно это отрезок [0;π], на котором функция обратима.
График функции y=arccos(x):
Например, чтобы найти arccos(1), можно воспользоваться равенством 1=cos(y). Угол на отрезке [0;π], косинус которого равняется 1, будет равен 0.
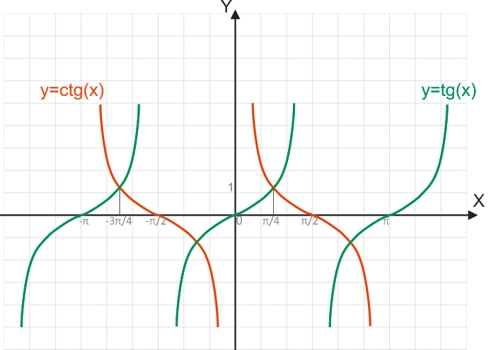
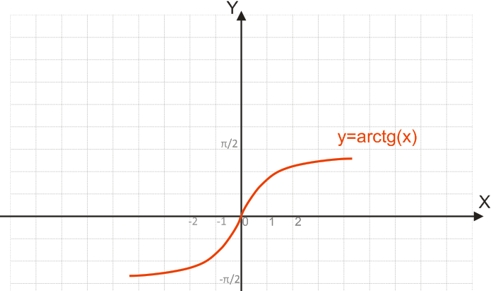
Функция y=arctg(x)
Поскольку функция y=tg(x) является периодической, она не является обратимой.
Для построения функции, обратимой y=tg(x), необходимо рассматривать тангенсоиду на отрезке [-π/2;π/2], на котором функция обратима.
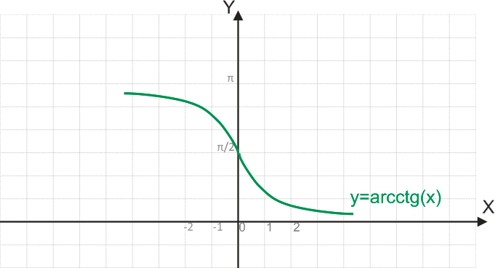
График функции y=arctg(x):
Функция y=arcctg(x)
Поскольку функция y=ctg(x) является периодической, она не является обратимой.
Для построения функции, обратимой y=ctg(x), необходимо рассматривать котангенсоиду на отрезке [0;π], на котором функция обратима.
График функции y=arcctg(x):
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
Конспекты уроков по теме «Обратная функция» (10 класс)
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Конспекты уроков по теме «Обратная функции»
Урок 1. Лекция по теме «Обратная функция»
Цель: Сформировать теоретический аппарат по теме. Ввести
— понятие обратимой функции;
— понятие обратной функции;
— сформулировать и доказать достаточное условие обратимости
— основные свойства взаимно обратных функций.
Актуализация знаний учащихся, необходимая для восприятия новой темы.
Постановка цели перед учащимися.
Изложение нового материала.
Подведение итогов урока.
Постановка домашнего задания.
1. Организационный момент.
Приветствие учителя, проверка готовности обучающихся к уроку.
2. Актуализация знаний. ( Фронтальный опрос по теме предыдущего урока.)
Для учащихся на интерактивной доске демонстрируется график функции (рис. 1). Учителем формулируется задание – рассмотреть график функции и перечислить изученные свойства функции. Учащиеся перечисляют свойства функции в соответствии со схемой исследования. Учитель справа от графика функции маркером на интерактивной доске записывает названные свойства.
D(f) = [-4; 

Ни четная, ни нечетная, непериодическая, непрерывная, ограничена снизу.
y>0 при на [-4;0) и на (0; 
Возрастает на (-2;-1) и на (0; 
убывает на (-4;-2) и на (-1;0).
Выпукла вниз на (4;-1), выпукла вверх на (1; 
3. Постановка цели перед учащимися.
По окончании исследования учитель сообщает, что сегодня на уроке они познакомятся еще с одним свойством функции – обратимостью. Для осмысленного изучения нового материала учитель предлагает ребятам познакомиться с основными вопросами, на которые учащиеся должны дать ответ по окончании урока. Вопросы в виде раздаточного материала есть у каждого ученика (раздается до урока).
1. Какая функция называется обратимой?
2. Какая функция называется обратной?
3. Как связаны между собой области определения и множества значений прямой и обратной функций?
4. Сформулируйте достаточное условие обратимости функции.
5. Функция обратная возрастающей является убывающей или возрастающей?
6. Функция обратная нечетной является четной или нечетной?
7. Как расположены графики взаимно обратных функций?
4. Изложение нового материала.
1) Понятие обратимой функции. Достаточное условие обратимости.
Затем учитель формулирует определение обратимой функции и проводит доказательство теоремы об обратимой функции, используя график монотонной функции на интерактивной доске.
Таким образом, разным значениям аргумента соответствуют разные значения функции, т.е. функция обратима.
Аналогично доказывается теорема в случае убывающей функции.
(По ходу доказательства теоремы учитель маркером делает все необходимые пояснения на чертеже)
Перед тем как сформулировать определение обратной функции учитель просит учащихся определить, какая из предложенных функций обратима? На интерактивной доске показаны графики функций (рис. 3, 4) и записаны несколько аналитически заданных функций:
а ) 
Замечание. Монотонность функции, является достаточным условием существования обратной функции. Но оно не является необходимым условием.
Учитель приводит примеры различных ситуаций, когда функция не монотонна, но обратима, когда функция не монотонна и не обратима, когда монотонна и обратима.
2) Понятие обратной функции. Алгоритм составления обратной функции.
Затем учитель знакомит учащихся со способом нахождения обратной функции, заданной аналитически.
На конкретных примерах учитель показывает как использовать данный алгоритм.
Пример 1. Показать, что для функции y=2x-5 существует обратная функция, и найти ее аналитическое выражение.
Пример 2. Показать, что для функции y=x 2 , х ≤ 0 существует обратная функция, и найти ее аналитическое выражение.
3) Свойства взаимно обратных функций.
Свойство 2. Если функция возрастает (убывает) на множестве Х, а У – область значений функции, то обратная функция возрастает (убывает) на У.
Свойство 4. Если нечетная функция обратима, то обратная ей тоже нечетная.
5 . Подведение итогов
Проведение диагностической работы. Целью этой работы является определение уровня усвоения учебного материала, рассмотренного на лекции. Учащимся предлагается ответить на вопросы, сформулированные в начале лекции.
6 . Постановка домашнего задания.
1. Разобраться с материалом лекции, выучить основные определения и формулировки теорем.
2. Доказать свойства взаимно обратных функции.
Урок 2. Практикум по теме «Определение обратной функции. Достаточное условие обратимости функции»
Цель: сформировать умения применять теоретические знания по теме при решении задач, рассмотреть основные типы задач на исследование функции на обратимость, на построение обратной функции.
1. Организационный момент.
2. Актуализация знаний (фронтальная работа учащихся).
3. Закрепление изученного материала (решение задач).
4. Подведение итогов урока.
5. Постановка домашнего задания.
1. Организационный момент.
Приветствие учителя, проверка готовности обучающихся к уроку.
2. Актуализация знаний. ( фронтальная работа учащихся).
Учащимся предлагается выполнить устно следующие задания:
1. Сформулируйте достаточное условие обратимости функции.
2. Среди функций, графики которых изображены на рисунке укажите те, которые являются обратимыми.
3. Сформулируйте алгоритм составления функции, обратной данной.
4. Существуют ли функции, обратные данным? В случае положительного ответа, найдите их:
5. Являются ли функции, графики которых изображены на рисунке, взаимно обратными (рис. 6)? Ответ обоснуйте.
3. Закрепление изученного материала (решение задач).
Закрепление изученного материала состоит из двух этапов:
— индивидуальная самостоятельная работа учащихся;
— подведение итогов индивидуальной работы.
На первом этапе учащимся предлагаются карточки с заданиями, которые они выполняют самостоятельно.
Является ли функции обратимыми на всей области определения? Если да, то найдите обратную к ней.
Являются ли взаимно обратными функции:
Рассмотрите функцию на каждом из указанных промежутков, если на этом промежутке функция обратима, то задайте обратную ей аналитически, укажите область определения и область значений:
Докажите, что функция необратима. Найдите функцию обратную ей на промежутке и постройте ее график.
Постройте график функции и определите, существует ли для нее обратная функция. Если да, то на том же чертеже постройте график обратной функции и задайте ее аналитически:
На этапе подведение итогов индивидуальной работы учащихся проверка задач осуществляется только с фиксированием промежуточных результатов. Задачи, вызвавшие больше всего затруднений, рассматриваются на доске либо с раскрытием поиска решений, либо с записью всего решения.
4. Подведение итогов урока (рефлексия).
Учащимся предлагается мини-анкета:
— Что мне понравилось на уроке?______________________________
— Что мне не понравилось на уроке?_____________________________
— Укажите одно наиболее подходящее вам утверждение:
1) Я могу самостоятельно исследовать функцию на обратимость, строить обратную и уверен в правильности результата.
2) Я могу исследовать функцию на обратимость, строить обратную, но не всегда уверен в правильности результата, нуждаюсь в помощи товарищей.
3) практически не могу исследовать функцию на обратимость, строить обратную, нуждаюсь в дополнительной консультации учителя.
— Где я смогу применять полученные знания?____________________ __________________________________________________________________
5. Постановка домашнего задания.
Обратная функция
Что такое обратная функция? Как найти функцию, обратную данной?
Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо :
1) В формулу функции вместо y подставить x, вместо x — y:
2) Из полученного равенства выразить y через x:
Найти функцию, обратную функции y=2x-6.
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.
Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).
y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая. Для построения прямой берём две точки.

Теорема (необходимое и достаточное условие обратимости функции)
Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.
Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.
Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.
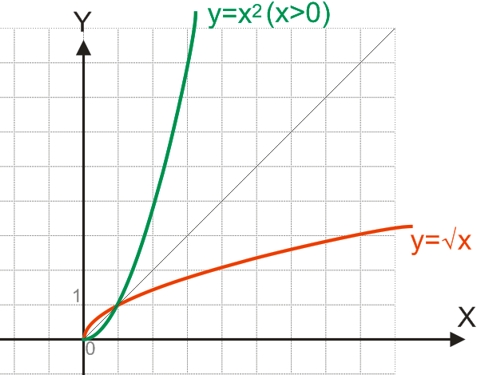
Классический пример — функция y=x². На промежутке [0;∞) функция возрастает. Условие обратимости выполнено, следовательно, можем искать обратную функцию.
Так как область определения функции y=x² — промежуток [0;∞), область значений на этом промежутке — также [0;∞), то область определения и область значений обратной функции — также [0;∞).
то есть на промежутке [0;∞) y=√x — функция, обратная к функции y=x². Их графики симметричны относительно биссектрисы I и III координатных четвертей:
В алгебре наиболее известными примерами взаимно обратных функций являются показательная и логарифмическая функция, а также тригонометрические и обратные тригонометрические функции.
1 комментарий
Для физических задач говорить об обратной функции, думаю, можно лишь для безразмерных у и х. При различии их размерностей, значит, и осей их графиков, надо для обратной функции поворачивать и оси.
Тогда лучше говорить о выражении аргумента х в явном виде, не упоминая об обратной функции. Значит, надо функцию у=ах/С+в, где х и С имеют, например, одинаковую размерность (например, кг), представить в виде уравнения ах/С+в-у=0. Из него можно выразить в явном виде у или х. Тогда либо у, либо х надо будет считать функцией с собственной координатной осью с собственной размерностью. При этом ось функции обычно является вертикальной.
Вопрос: можно ли считать выраженные в явном виде функции у и х обратными?