Что такое обратная геодезическая задача
Прямая и обратная геодезические задачи. Их применение в геодезическом производстве



а) Прямая геодезическая задача
Рис. 3.5. Прямая геодезическая задача
Дано: координаты точки 1 х1, у1; горизонтальное проложение линии 1 – 2: d1,2;
дирекционный угол линии 1 – 2: a1,2 (рис.3.5).
Найти: координаты точки 2: х2, у2.
Решение: координаты точки 2: х2 = х1 + Dх; у2 = у1 + Dу, (3.6)
где приращения координат Dх = d · cos a; Dу = d · sin a, (3.7)
Знаки приращений координат Dх и Dу зависят от знаков функций sin a и cos a.
б) Обратная геодезическая задача
 |
Рис. 3.6. Обратная геодезическая задача
Найти: горизонтальное проложение линии 1 – 2: d1,2; дирекционный угол линии 1 – 2: a1,2.
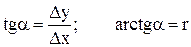
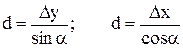
По значению tg a определяется румб линии. По знакам приращений координат определяется четверть, а по четверти определяется дирекционный угол линии.
Рис. 3.7. Знаки приращений координат в зависимости от четверти
Прямая геодезическая задача применяется при вычислении координат в теодолитном ходе. Обратная геодезическая задача применяется в тех случаях, когда по известным координатам 2-х точек определяют расстояние между ними и дирекционный угол линии.
Тема: Основы математической обработки результатов теодолитной съёмки. Вычисление координат вершин теодолитного хода. Составление плана
1. Проверка полевых вычислений и определение поправок в измерения длин линий
_______ Далее вычисляются средние значения длин линии:
 |
_______ В каждую длину линии вводятся поправки по формуле:
 |
_______ Поправки вводятся при:
 |
_______ После уравнивания углов производится вычисление дирекционных углов всех сторон теодолитного хода. _______ Вычисленные дирекционные углы переводятся в румбы.
2. Связь между дирекционными углами и горизонтальными углами теодолитного хода
 |
 |
_______ Дирекционный угол линии последующей равен дирекционному углу линии предыдущей плюс 180 0 минус угол вправо по ходу лежащий.
3. Обработка угловых измерений замкнутого теодолитного хода
 |
 |
_______ где fβ – угловая невязка.
 |
_______ где n –вершина углов, следовательно:
 |
4. Угловая невязка разомкнутого теодолитного хода
 |
Для вычисления ∑β теор. найдем дирекционные углы всех сторон хода:
 |
 |
 |
 |
_______ где αнач. и αкон. – дирекционные углы сторон опорной сети, тогда:
 |
5. Невязки в диагональном ходе
 |
 |
_______ После обработки угловых измерений вычисляются дирекционные углы и румбы всех сторон хода.
6. Прямая и обратная геодезические задачи
6.1. Прямая геодезическая задача: по координатам отрезка прямой (начала), его длине и направлению определить координаты конца отрезка
 |
 |
_______ Прямая геодезическая задача применяется при вычислении координатных точек теодолитного хода.
6.2. Обратная геодезическая задача: по координатам начала и конца отрезка прямой найти его длину и направление
 |
 |
_______ Далее вычисляют arctg и находят числовое значение румба. Название румба определяют по знакам приращений координат, от румба переходят к дирекционному углу.
Длина линии может быть найдена по следующим формулам:
 |
_______ Обратная геодезическая задача применяется при подготовке данных для перенесения проектов сооружений в натуру.
7. Уравнивание приращений координат
_______ Уравниванием называется совокупность математических операций, выполняемых для получения вероятнейшего значения геодезических координат точек земной поверхности и для оценки точности результатов измерений.
_______ Уравнивание проводится для устранения невязок, обусловленных наличием ошибок в избыточно измеренных величинах, и для определения вероятнейших значений искомых неизвестных или их значений, близких к вероятнейшим. В процессе уравнвиания это достигается путём определения поправок к измеренным величинам (углам, направлениям, длинам линий или превышениям).
7.1. Вычисление координат точек теодолитного хода
 |
_______ Из решения прямой геодезической задачи по известным длинам сторон и румбам вычисляются приращения координат для каждой стороны хода по формулам:
 |
_______ Далее вычисляются невязки в приращениях координат замкнутого хода.
7.2. Вычисление невязок в приращениях координат замкнутого хода
_______ Из геометрии известно, что сумма проекций сторон многоугольника на любую ось равна нулю, следовательно:
 |
_______ Под влиянием ошибок измерений замкнутый полигон будет разомкнутым на величину fр – абсолютная невязка в периметре полигона.
 |
 |
_______ Если полученная невязка недопустима, то необходимо произвести повторное измерение длин линий.
_______ Если невязки допустимы, то они распределяются на приращения координат пропорционально длинам сторон с противоположным знаком, то есть сумма исправленных приращений должна быть точно равна теоретической сумме – в данном случае равна нулю.
7.3. Вычисление невязок в приращениях координат разомкнутого теодолитного хода
_______ Определение допустимости невязок и их распределения производится так же, как для замкнутого теодолитного хода.
 |
 |
Для диагонального хода, например:
 |
 |
_______ По исправленным значениям приращений координат вычисляются координаты всех точек хода по формулам:
 |
8. Построение плана
_______ Построение плана выполняются в следующей последовательности :
1) построение координатной сетки,
2) нанесение вершин теодолитного хода по координатам,
3) нанесение на план контуров местности,
4) оформление плана.
8.1. Построение координатной сетки
_______ 1) построение сетки с помощью линейки Дробышева:
 |
_______ Построение сетки основано на построении прямоугольного треугольника с катетами 50×50 см и гипотенузой 70,711 см ;
2) построение сетки с помощью циркуля, измерителя и масштабной линейки:
 |
_______ Вершины теодолитного хода наносятся на план по координатам относительно сетки с помощью измерителя и поперечного масштаба.
_______ Контроль правильности построения точек выполняется по известным расстояниям между точками. Допустимое расхождение – 0,3 мм в масштабе плана.
_______ Контуры местности наносятся на план в соответствии с абрисами.
_______ Оформление плана выполняется в строгом соответствии с условными знаками, установленными для данного масштаба.
ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА. Методические указания с вариантами для решения.
Методические указания предназначены для обеспечения самостоятельной работы студентов при решении Обратной геодезической задачи.
Просмотр содержимого документа
«ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА. Методические указания с вариантами для решения.»
Обратная геодезическая задача.
Порядок выполнения работы………………………………….5
Список использованной литературы…………………………24
Методические указания предназначены для обеспечения самостоятельной работы студентов при решении Обратной геодезической задачи. Данная задача широко представлена, как на втором, так и на третьем курсах специальности
№ 120301 «Землеустройство». В методических указаниях подробно рассмотрен порядок решения обратной геодезической задачи. Для обеспечения самостоятельной работы прилагается 100 вариантов для решения задачи, с ответами (приложения №1,2). Данная работа поможет преподавателю, так как раздаточного материала хватит на три учебных группы и все варианты имеют ответы.
Цель работы – оказать помощь студентам при самостоятельном решении Обратной геодезической задачи.
Согласно Государственного образовательного стандарта СПО студент должен:
иметь представление о сфере применения данной задачи;
знать способы решения обратной геодезической задачи;
уметь правильно оформить результаты вычислений и произвести контроль с использованием вычислительной техники.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Раздел IX. Геодезические работы при землеустройстве.
Тема 9.3 Геодезические работы при перенесении проектов внутрихозяйственного землеустройства в натуру.
Практическая работа. Решение обратных геодезических задач при подготовке геоданных для перенесения проекта в натуру.
Задание: выполнить решение обратных геодезических задач для подготовки геоданных.
Исходные данные: приложение №1, по вариантам.
Обратная геодезическая задача.


Для вычисления румба в градусной мере необходимо выполнить на микрокалькуляторе следующие операции:
4. Дирекционный угол линии АВ (αАВ)
в

Формулы для вычисления дирекционного угла линии по румбу.
8. 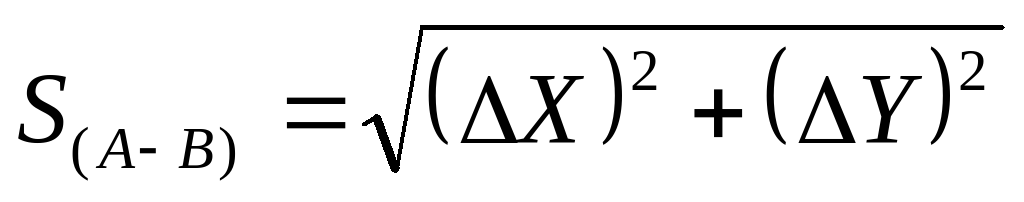
9. SAB ср. вычисляется, как среднее из трёх
полученных значений расстояния АВ.

XA = 28359.109 м 1. X = XB – XA=29007.458 – 28359.109 = 648.349м.
YA = 29408.251 м 2. Y = YB – YA=29903.074 – 29408.251 = 494.823м.
XB = 29007.458 м 3. tg (rАВ) = ΔY : ΔX = 0.7632047;
YB = 29903.074 м 4. rАВ = СВ : 37 ˚ 21 ´ 03. ´´ 8 ;

8. 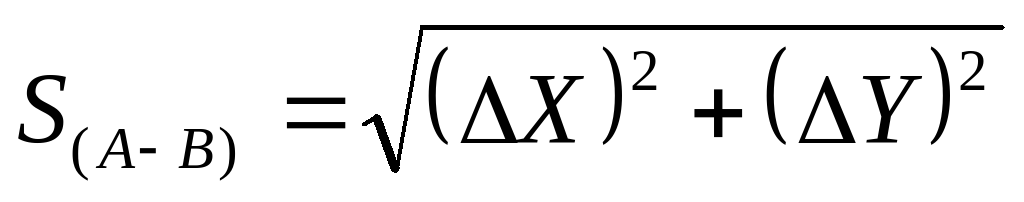
Образец формуляра для решения обратной геодезической задачи.
ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА. Методические указания с вариантами для решения.
Методические указания предназначены для обеспечения самостоятельной работы студентов при решении Обратной геодезической задачи.
Просмотр содержимого документа
«ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА. Методические указания с вариантами для решения.»
Обратная геодезическая задача.
Порядок выполнения работы………………………………….5
Список использованной литературы…………………………24
Методические указания предназначены для обеспечения самостоятельной работы студентов при решении Обратной геодезической задачи. Данная задача широко представлена, как на втором, так и на третьем курсах специальности
№ 120301 «Землеустройство». В методических указаниях подробно рассмотрен порядок решения обратной геодезической задачи. Для обеспечения самостоятельной работы прилагается 100 вариантов для решения задачи, с ответами (приложения №1,2). Данная работа поможет преподавателю, так как раздаточного материала хватит на три учебных группы и все варианты имеют ответы.
Цель работы – оказать помощь студентам при самостоятельном решении Обратной геодезической задачи.
Согласно Государственного образовательного стандарта СПО студент должен:
иметь представление о сфере применения данной задачи;
знать способы решения обратной геодезической задачи;
уметь правильно оформить результаты вычислений и произвести контроль с использованием вычислительной техники.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Раздел IX. Геодезические работы при землеустройстве.
Тема 9.3 Геодезические работы при перенесении проектов внутрихозяйственного землеустройства в натуру.
Практическая работа. Решение обратных геодезических задач при подготовке геоданных для перенесения проекта в натуру.
Задание: выполнить решение обратных геодезических задач для подготовки геоданных.
Исходные данные: приложение №1, по вариантам.
Обратная геодезическая задача.


Для вычисления румба в градусной мере необходимо выполнить на микрокалькуляторе следующие операции:
4. Дирекционный угол линии АВ (αАВ)
в

Формулы для вычисления дирекционного угла линии по румбу.
8. 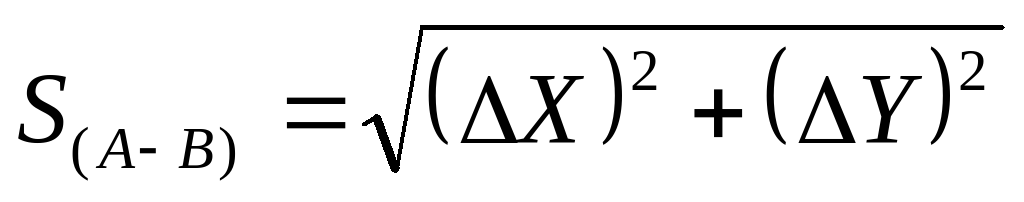
9. SAB ср. вычисляется, как среднее из трёх
полученных значений расстояния АВ.

XA = 28359.109 м 1. X = XB – XA=29007.458 – 28359.109 = 648.349м.
YA = 29408.251 м 2. Y = YB – YA=29903.074 – 29408.251 = 494.823м.
XB = 29007.458 м 3. tg (rАВ) = ΔY : ΔX = 0.7632047;
YB = 29903.074 м 4. rАВ = СВ : 37 ˚ 21 ´ 03. ´´ 8 ;

8. 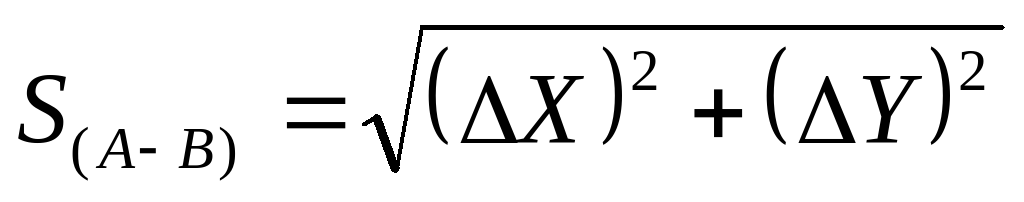
Образец формуляра для решения обратной геодезической задачи.
Тема 3. Прямая и обратная геодезическая задача.
При производстве строительных работ создается разбивочная основа в виде строительной сетки. Пункт Государственной геодезической сети выносится на территорию строительства для обеспечения исходными данными всех геодезических работ. Решение прямой геодезической задачи позволяет определить координаты всех точек, расположенных в зоне строительства.
При составлении планов ситуацию накладывают от опорных точек и линий, их соединяющих. Поэтому на бумагу сначала наносят опорные точки по их координатам. Так как число этих точек весьма велико, то при геодезических работах часто решают прямую задачу на координаты. Она состоит в том, что по известным координатам данной точки, а также дирекционному углу и горизонтальному проложению линии от этой точки до определяемой вычисляют координаты определяемой точки.
Решить прямую геодезическую задачу, т.е Пример
определить прямоугольные координаты точки 2 через координаты точки 1 по следующим данным:
Расстояние между точками d =120,10 м; направление линии, т.е дирекционный угол 48°30′ =r.
1.Определяем приращение координат ΔХ =d . cosr = 120,10 . 0,6626 =79,51 м
ΔУ= d . sinr =12,10 . 0,7490 =89,95 м
ΔУ




х1 1
2. Определяем координаты точки 2
В практике прикладной геодезии для нужд проектирования и выноса проекта на местность приходиться определять значения дирекционного угла и длинны стороны по известным координатам её конечных точек. Это и составляет сущность решения обратной геодезической задачи.
Решение обратной геодезической задачи состоит в том, что, зная координаты опорных точек, можно вычислить дирекционный угол и расстояние между данными точками.
Пример.
Решить обратную геодезическую задачу, т.е. найти расстояниеd между точками и направление этой линии ( румб, азимут), если координаты точки1 Х1= 320,5 м, У1 = 780,2 м; координаты т очки 2 Х2= 230,7 м, У2 =900,1 м.
ΔХ = У2 –У1 =900,1 – 780,2 = 119,9 м
Знаки приращений говорят, что линия расположена во второй четверти (ЮВ)
Знаки приращения координат можно определить по следующей схеме:

Они зависят от четверти, в которой расположена линия.
2. Величина румба определяется по формуле
tg r= 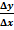
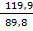
ctgr = 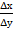
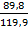
3. Расстояние между точками найдем по теореме Пифагора:
d= 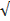
Контрольные вопросы:
1. Какие знаки у приращения координат ΔХ и ΔУ, если наименование румба ЮЗ?
а) –ΔХ, –ΔУ; б)+ ΔХ, +ΔУ; в)–ΔХ,+ΔУ; г))+ ΔХ,–ΔУ;
2. Найдите координаты точки 2, если координаты точки 1 Х= 10, У=5 и приращение ΔХ = 20, ΔУ =15.
а) 30, 20; б) 20, 30; в) 20, 40; г) 30, 40;
3. Решить обратную геодезическую задачу: найти расстояние между двумя точками и румб линии, если координаты начала и конца линии Х1= 320,5 м, У1 = 780,2 м; Х2 230,7 м,
а); 160,7 м, 60⁰ 20ʹ; б)149,8 м, 53⁰ 10ʹ; в) 120, 9 м, 58⁰ 45ʹ; г) 456,7м, 45⁰ 15ʹ;
| № | Вопросы (задания) | Ответы | Код |
| I | Осевого меридиана зоны | 1 | |
| Ближайшего направления меридиана | 2 | ||
| Южного направления магнитного меридиана | 3 | ||
| Северного направления географического меридиана | 4 | ||
| II | Азимут лини находиться в пределах от 180°-270° | Сз | 1 |
| каково наименование румба? | Юв | 2 | |
| Юз | 3 | ||
| Св | 4 | ||
| III | r°=А° | 1 | |
| r°=180°-А° | 2 | ||
| r°=А°-180° | 3 | ||
| r°=360°-А° | 4 | ||
| IV | каково градусное значение азимута (А°) линии для ЮВ:r | А°=180°+r° | 1 |
| А о =360°-r° | 2 | ||
| А°=180°-r° | 3 | ||
| А°=r° | 4 | ||
| V | Сз:r° | 1 | |
| Юз:r° | 2 | ||
| Юв:r° | 3 | ||
| Св:r° | 4 |
| № | Вопросы (задания) | Ответы | Код |
| I | Какие слова нужно вставить в место точек в определении «Дирекционным углом лини называют угол, отсчитанный от. до данной прямой по направлению часовой стрелки?» | Северного направления географического меридиана | 1 |
| Осевого меридиана зоны | 2 | ||
| Южного | 3 | ||
| направления магнитного | |||
| меридиана | |||
| Ближайшего | 4 | ||
| направления меридиана | |||
| И | Азимут лини находиться в пределах от 0°-90° каково наименование румба? | Сз | 1 |
| Юв | 2 | ||
| Юз | 3 | ||
| Св | 4 | ||
| III | r°=А° | 1 | |
| r°=180°-А° | 2 | ||
| r°=А°-180° | 3 | ||
| r°=360°-А° | 4 | ||
| IV | каково градусное значение азимута (А°) линии для Юз:ч° | А°=180°-r° | 1 |
| А°-360°-r° | 2 | ||
| A°=180W | 3 | ||
| А°=r° | 4 | ||
| V | Сз:r° | 1 | |
| Юз:r° | 2 | ||
| Юв:r° | 3 | ||
| Св:r° | 4 |
| № | Вопросы (задания) | Ответы | Код |
| I | Какие слова нужно вставить в место точек в определении «Дирекционным углом лини называют угол, отсчитанный от. до данной прямой по направлению часовой стрелки?» | Северного направления географического меридиана | 1 |
| Южного | |||
| направления магнитного | 2 | ||
| меридиана | |||
| Ближайшего | |||
| направления меридиана | 3 | ||
| Осевого | 4 | ||
| меридиана зоны | |||
| И | Азимут лини находиться в пределах 90°-180 каково | Сз | 8 |
| наименование румба? | Юв | 9 | |
| Юз | 1 | ||
| Св | 2 | ||
| III | r°=А° | 3 | |
| r°=180°-А° | 4 | ||
| r°=А°-180° | 5 | ||
| r°=360°-А° | 6 | ||
| IV | каково градусное значение азимута (А°) линии для румба св: r° | А°=180°-r° | 7 |
| А°=360°-r° | 8 | ||
| А°=180°+r° | 9 | ||
| А°=r° | 1 | ||
| V | Сз:r° | 2 | |
| Юз:r° | 3 | ||
| Юв:r° | 4 | ||
| Св:r° | 5 |
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.